Geum.ru

Методическая разработка

Вид материалаМетодическая разработка
Подобный материал:
1   2   3   4   5   6
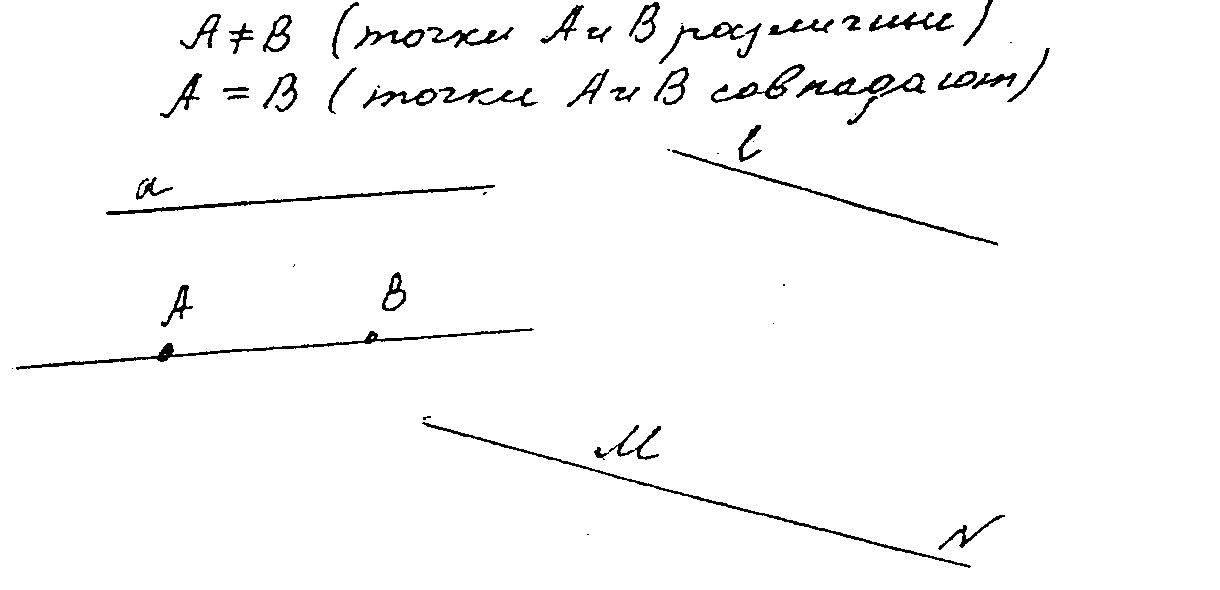читель чертят прямую и обозначает ее строчной буквой. Затем учитель отмечает несколько точек на прямой и точки вне прямой и поясняет записи. Образец записи в тетради учащихся:

Точки: А, В, С, D, М, Е,

Прямые: а, в, с, l, d,
или: AB, MN, LK, ОР.

K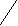€a; M€a

3 Практическая работа

Упражнение 1. Изобразить прямую. Отметить несколько точек на прямой и вне прямой.

Вопрос: если изображена прямая, то всегда ли можно ука­зать точки, принадлежащие ей, и точки, не при­надлежащие ей?

Упражнение 2. Изобразить прямую и отметить на ней три произвольные точки А, В и С. (Учитель объясняет запись А-В-С: точка В лежит между точками А и С).

Вопрос: Всегда ли из трех точек на прямой одна лежит между двумя другими?

Упражнение 3. Изобразите две различные прямые, а) не имеющие общей, точки (прямые не пересекаются). Вспомните запись a||b Учитель объясняет запись a∩b.
б) Изобразите две пересекающиеся прямые (прямые имеют общую точку). Учитель объясняет запись a∩b=A.
в) Изобразите две прямые, имеющие бесконечно много общих точек (прямые совпадают). Учитель объясняет запись a=b.
Вопрос: могут ли две различные прямые иметь более двух общих точек?

Урок можно завершить работой по карточкам. Учащиеся должны ответить на вопросы 1, 2, 3, 5.

Образец карточки первого варианта. Дан рисунок:



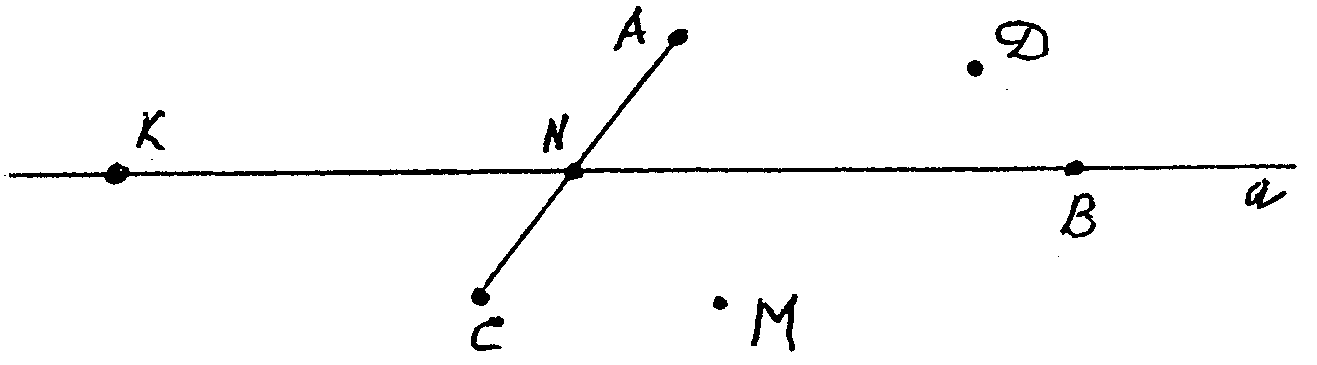
Вопросы: 1. Назовите точки, принадлежащие и не принадлежащие прямой а.
2. Сколько прямых можно провести через K и B, C и M?
3. Имеют ли и сколько точек пересечения прямые KB и СА?
4. Какая точка лежит между точками K и B, C и A?

Проверка работы осуществляется с помощью диапроектора или доски, на которой задания по четырем вариантам выполняли учащиеся.

Вопросы (на дом): 1. Сколько прямых можно провести через а) одну точку, б) две точки, в) три точки?
2. Сколько точек пересечения могут иметь три прямые, каждые две из которых пересекаются?
З. Сколько точек пересечения имеют четыре попарно пересекающиеся прямые?
4. Сколько прямых могут определять пять точек на плоскости?

ПРЕДИСЛОВИЕ К УРОКУ №2.

Урок начинается с проверки домашнего задания. В период подготовки учащихся к ответу, проводится фронтальная беседа с классом. На этих этапах урока учитель работает над проверкой усвоения изученного мате­риала на прошлом занятии, закреплением понятий точка, прямая, "лежать между", "существует и притом только одна", умении пользоваться символами, введенными на прошлом уроке. Вопросы 3 и 4 из домашнего задания способствуют развитию интуиции, воображению и других важнейших качеств, лежащих в основе любого творческого процесса.

Основная часть урока - изучение понятий: луч, начало луча, дополнительные лучи. Изученный материал закрепляется диктантом. Проверка осуществляется по образцу. Работа по рисунку, ответы на вопросы, записи в тетради ученика, на диапозитиве (доске) - все это способствует запоминанию основного материала на длительный срок.

За 2-3 минуты до конца урока учащиеся записывают задание на дом.

Вводная беседа № 2

План. 1. Проверка домашней работы.
2. Проверка усвоения изученного материала на прошлом уроке
3. Луч, полупрямая.
4. Вопросы.

Примерное содержание вводной беседы

1. Четверым ученикам предлагается подготовить у доски рассказ о решении упражнений из домашнего задания (сделать рисунки).

2. В период подготовки учащихся к. ответу с классом проводится фронтальная беседа по готовому рисунку, который проектируется на экран.

Рисунок

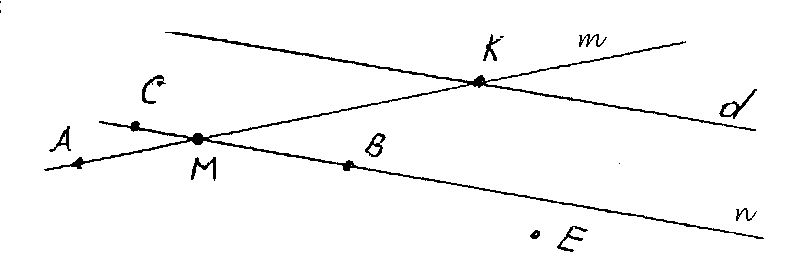
Задание: опишите ситуацию, заданную рисунком

Возможные ответы: 1. m∩n=M, d∩m=K.
2. Am, Km, Mm.
3. Cn, Mn, Bn.
4. En, Em.
5. A―M―K.
6. C―M―B.
7. d||n (d∩n=Ø)

3. Практическая работа.

Упражнение I. Изобразите прямую на плоскости. Отметьте на ней точку Е
Вопрос: что сделала точка Е с прямой?

а1- и a2 ― полупрямые

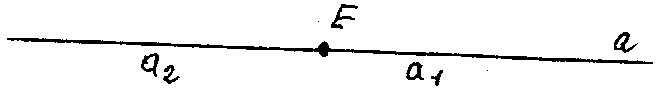
Любая точка прямой разбивает ее на две части. Одна из частей этой прямой - полупрямая, или открытый луч (a1 - открытый луч).

Упражнение 2. Изобразите прямую KN и точку C, принадлежащую прямой KN, причем K-C-N.
Вопрос: назовите полупрямые. Сколько их? Что можно сказать о точке C и каждом из открытых лучей?

Точку C можно отнести к одному из открытых лучей. Если точка отнесена к полупрямой, то полупрямая станет замкнутым лучом и точка его началом (замкнутый луч будем называть лучом)

Упражнение 3. Отметьте две точки C и D. Начертите полупрямую CD. Отметьте точку E, не принадлежащую CD. Постройте луч C
Вопрос: Пересекаются ли лучи CE и CD? Пересекаются ли полупрямая CD и луч CE? Назовите лучи с начальной точкой E на полупрямой CE.

Лучи могут лежать на одной прямой или не лежать на одной прямой, причем, если два луча лежат на одной прямой, то



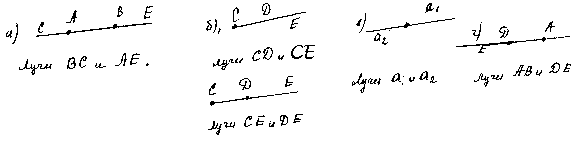
Вопрос: Что является общей частью для двух лучей в каждом из случаев а), б), в).

Упражнение 4. Начертите прямую, отметьте точку B на этой прямой. Вопросы: Назовите лучи с началом в точке В. Как расположены эти лучи?

Лучи ВК и ВЕ - дополнительные лучи.

Упражнение 5. Отметьте две точки М и С, постройте луч МС. Начертите луч, дополнительный к лучу МС. Вопрос: Сколько таких лучей можно построить?

Урок можно завершить диктантом,

Текст диктанта.

Рисунок.