П падение тела

Вид материала

Документы

Содержание В. Н. Колесников. А. П. Лееанюк. Пито трубка Плавание тел Рис. 2. Силы, действующие на тело, погру­жённое в жидкость до грузовой ватерлинии аb. Т — темп-pa, х — состав раствора (относит. кол-во компоненты В в компоненте А). Рис. 3. Остановка изменения темп-ры при плавлении крист. тела. По оси абсцисс от­ложено время , пропорциональное равно­мерно по Рис. 4. Изменение темп-ры плавления Т Б. Я. Любое. В на ч-цы П. действует Лоренца сила Рис. 2. Вращение ионов и эл-нов по ларморовским спиралям. Радиус враще­ния иона (е>0) больше радиуса вращения эл-на (е Рис. 3. Эл-н, про­летающий мимо ио­на, движется по ги­перболе.  — угол отклонения. Рис. 4. Движение си­ловых линий магн. поля B вместе с плаз­мой (св-во вмороженности силовых ли­ний), в — скорость среды. Рис. 5. Движение косм. ч-ц, захвачен­ных магн. полем Зем­ли. Рис. 6. Образование перетяжек на канале разряда, сжатого соб­ственным магн. полем: I — ток; В — индук­ция магн. поля, равная нул Рис. 7. Токамак. Токи, текущие в проводящем кожухе, препятствуют смещению плазменного шнура. Рис. 8. Синусоидаль­ный профиль плотно­сти эл-нов в монохроматич. плазмен­ной волне. Диагностика плазмы. Применение плазмы. Рис. 9. Схема МГД-генератора, преобразую­щего кинетич. энергию движущейся плазмы в электрич. энергию. R — внеш. нагрузка генерат ... Полное содержание

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПИРОМЕТРЫ, приборы для измере­ния темп-ры нагретых тел по интенсив­ности их теплового излучения в оптич. диапазоне спектра. Тело, темп-ру к-рого определяют при помощи П., должно находиться в тепловом равно­весии и обладать коэфф. поглощения, близким к единице (см. Пирометрия). Применяют яркостные, цве­товые и радиационные П. Широко распространены яркостные П., обеспечивающие наибольшую точ­ность измерений темп-ры в диапазоне 10³—10⁴ К. В простейшем визуальном яркостном П. с исчезающей нитью объ­ектив фокусирует изображение иссле­дуемого тела на плоскость, в к-рой расположена нить (ленточка) спец. лампы накаливания. Через окуляр и красный фильтр, позволяющий выде­лять узкую спектр. область ок. дли­ны волны _э=0,65 мкм, нить рас­сматривают на фоне изображения те­ла и, изменяя ток накала нити, доби­ваются, чтобы яркости нити и тела были одинаковыми (нить становится неразличимой на фоне тела). Шкалу прибора, регистрирующего ток нака­ла, градуируют обычно в °С или К, и в момент выравнивания яркостей нити и тела прибор показывает т. н. яркостную температуру (Т_b) тела. Истинная темп-pa тела Т определя­ется на основе законов теплового излучения Кирхгофа и Планка по ф-ле:

T=T_bc₂/(c₂+_эln_,T), (1)

где c₂=0,01488 м•К (т. н. 2-я посто­янная излучения), _,T — коэфф. поглощения тела, _э — эффективная длина волны П.

Точность результата в первую оче­редь зависит от строгости выполнения условий пирометрич. измерений (коэфф. поглощения _,T близок к значению а абсолютно чёрного тела и др.). Для выполнения этих условий обычно наблюдают излучение, выхо­дящее из полости с небольшим выход­ным отверстием, имитирующим абсо­лютно чёрное тело. Осн. инструмен­тальная погрешность обусловлена нестабильностью температурной лам­пы. Заметную погрешность могут вносить также индивидуальные осо­бенности глаза наблюдателя. У фо­тоэлектрических П. этот вид погрешности отсутствует. Погреш­ность образцовых лаб. фотоэлектрич. П. не превышает сотых долей К при Т ~ 1000 К. Образцовые яркостные П. приняты в качестве осн. интерполя­ционных приборов, определяющих Международную практическую темпе­ратурную шкалу (МПТШ-68) при теми-pax выше точки затвердевания золота (1064,43°С).

533


Для измерения темп-ры тел, у к-рых коэфф.  постоянен в оптич. диа­пазоне спектра, применяют цвето­вые П. Этими П. определяют отно­шение яркостей b₁(₁,T)/b₂(₂,Т) обычно в синей и красной областях спектра (напр., для длин волн ₁=0,48 мкм и ₂=0,60 мкм). Шкала прибора градуирована в °С и показы­вает цветовую температуру Т_с. Ис­тинная темп-pa Т тела определяется по ф-ле:



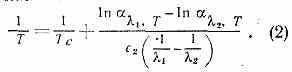
Точность цветовых П. ниже, чем у яркостных.

Наиболее чувствительны (но и наи­менее точны) радиац. П., или П. суммарного излучения, регистрирую­щие полное излучение тела. Действие их основано на Стефана — Больцмана законе излучения и Кирхгофа законе излучения. Объектив радиац. П. фоку­сирует наблюдаемое излучение на приёмник (обычно термостолбик или болометр), сигнал к-рого регистри­руется прибором, калиброванным по излучению абсолютно чёрного тела и показывающим радиационную темпе­ратуру Т_r. Истинная темп-pa тела определяется по ф-ле:

Т=^1/4_TТ_r, (3)

где _T— полный коэфф. поглощения тела. Радиац. П. можно измерять темп-ру начиная с 200°С. В пром-сти этот П. широко применяют в системах контроля и управления температур­ными режимами разнообразных технологич. процессов.

• Р и б о Г., Оптическая пирометрия, пер. о франц., М.—Л., 1934; Гордов А. Н., Основы пирометрии, 2 изд., М., 1971.

В. Н. Колесников.

ПИРОЭЛЕКТРИКИ, кристаллич диэлектрики, обладающие спонтан­ной поляризацией, т. е. поляризаци­ей в отсутствии электрич. поля и др. внеш. воздействий. Спонтанная поляризация — результат несовпадения «центров тяжести» положит. и отрицат. зарядов.



Обычно наблюдается не сама спонтанная поляризация Р (она компенсируется полями свободных электрич. зарядов, натекающих на

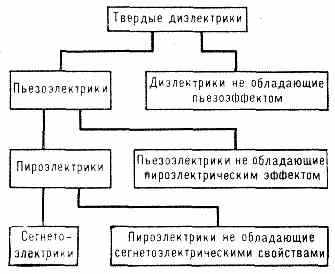
поверхность П. изнутри и извне), а её изменение Р при быстром изменении темп-ры T (пироэлектрич. эффект). Плотность возникающего поверхност­ного заряда =рT наз. пиро­электрической констан­той р. Типичный П.— турмалин; в нём при изменении темп-ры на 1°С возникает электрич. поле Е ~400 В/см. П. могут быть лишь нецентросимметричные кристаллы. Измене­ние поляризации в П. может происхо­дить и под действием механич. нап­ряжений (пьезоэлектрич. эффект). Все П. явл. пьезоэлектриками, но не наоборот; нек-рые П. обладают сегнетоэлектрич. св-вами (рис.).

П. используются в технике в кач-ве индикаторов и приёмников излучений. • См. лит. при ст. Диэлектрики.

А. П. Лееанюк.

ПИРОЭЛЕКТРИЧЕСТВО (пироэлек­трический эффект), появление элект­рич. зарядов на поверхности нек-рых кристаллов (пироэлектриков) при их нагревании или охлаждении. Один конец пироэлектрика при нагревании заряжается положительно, а при охлаждении отрицательно, другой -наоборот. Интенсивность электриза­ции максимальна, если скорость изме­нения темп-ры выше скорости релак­сации заряда. При изменении темп-ры на 1 К поверхностная плотность воз­никающего ряда, как правило, не превышает неск. сотен единиц (в системе СГСЭ). Появление зарядов на поверхности пироэлектрика свя­зано с изменением существующей в нём поляризации при изменении темп-ры кристалла.

ПИТО ТРУБКА, Г-образная трубка для измерения динамич. напора теку­щей жидкости (газа). Названа по имени её изобретателя франц. учёного А. Пито (Н. Pitot; 1732). Применя­ется также как составная часть Прандтля трубки. См. также Трубки из­мерительные.

ПЛАВАНИЕ ТЕЛ, состояние равно­весия тв. тела, частично или полностью погружённого в жидкость (или газ). Осн. задача теории П. т.— определе­ние положений равновесия тела, погружённого в жидкость, выяснение условий устойчивости равновесия. Простейшие условия П. т. указывает Архимеда закон.

Осн. понятия теории П. т. (рис. 1):

1) водоизмещение тела — вес жидко­сти, вытесняемой телом в состоянии равновесия (совпадает с весом тела);

2) плоскость возможной грузовой ватерлинии — всякая плоскость аb, отсекающая от тела объём, вес жид­кости в к-ром равен водоизмещению тела; 3) поверхность грузовых ва­терлиний — поверхность I, в каждой точке к-рой касательная плоскость явл. плоскостью возможной грузовой ватерлинии; 4) центр водоизмещения (или центр величины) — центр тяже­сти А объёма, отсекаемого плоскос­тью возможной грузовой ватерлинии; 5) поверхность центров водоизмеще­ния — поверхность II, являющаяся геометрич. местом центров водоиз­мещения.



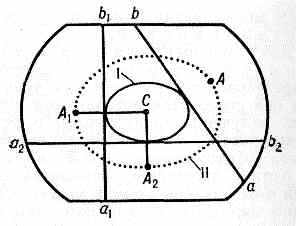
Рис. 1. ab, a₁b₁, а₂b₂ — плоскости воз­можной грузовой ватерлинии; А, А₁, А₂ — центры водоизмещения для объёмов, отсекаемых плоскостями аb, a₁b₁, a₂,b₂; I — поверхность грузовых ватерлиний; II — по­верхность центров водоизмещения.


Если тело погрузить в жидкость до к.-н. плоскости возможной грузовой ватерлинии аb (рис. 2), то на тело будут действовать направленная перпенди­кулярно этой плоскости (т. е. верти­кально вверх) поддерживающая сила F, проходящая через центр А, и чис­ленно равная ей сила тяжести Р. Как доказывается в теории П. т., направ­ление силы F совпадает одновремен­но с направлением нормали An к поверхности II в точке А.



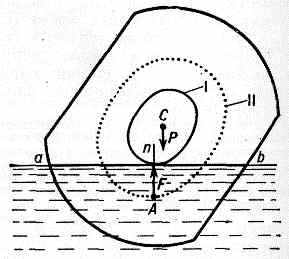
Рис. 2. Силы, действующие на тело, погру­жённое в жидкость до грузовой ватерлинии аb.


В положении равновесия силы F и Р должны быть направлены вдоль одной прямой, т. е. нормаль к по­верхности II, восстановленная из цен­тра А, должна проходить через центр тяжести С тела (нормали А₁С, А₂С на рис. 1). Число нормалей к поверх­ности II, проходящих через центр тя­жести С, даёт число возможных по­ложений равновесия плавающего тела. Если тело вывести из положения рав­новесия, то на него будет действовать пара сил F, Р. Когда эта пара стре­мится вернуть тело в положение рав­новесия, равновесие устойчиво, в про­тивном случае — неустойчиво. Об ус­тойчивости равновесия можно судить по положению метацентра. Другой простой признак: положение равнове­сия устойчиво, если для него расстоя­ние между центрами А и С явл. наи­меньшим по сравнению с этим расстоя­нием для соседних положений (на

534


рис. 1 при погружении до плоскости

а₂b₂ равновесие устойчиво, а до а₁b₁—

неустойчиво).

• Жуковский Н. Е., Теоретическая

механика, 2 изд., М.—Л., 1952.

С. М. Тарг.

ПЛАВЛЕНИЕ, переход в-ва из кристаллич. (твёрдого) состояния в жид­кое, происходит с поглощением теп­лоты (фазовый переход I рода). Гл. хар-ками П. чистых в-в явл. темпе­ратура плавления (T_пл) и теплота плавления (L_пл).

Темп-pa П. зависит от внеш. давле­ния р; на диаграмме состояния чис­того в-ва эта зависимость изобража­ется кривой плавления (кривой сосу­ществования тв. и жидкой фаз, AD или AD' на рис. 1). П. сплавов и тв. растворов происходит, как правило, в определённом интервале темп-р (исклю­чение составляют сплавы с пост. T_пл — эвтектики).



Рис. 1. Диаграмма состояния чистого в-ва (р — давление, T — темп-pa). Линии AD и AD' — кривые плавления, по линии AD' плавятся в-ва с аномальным изменением объ­ёма при плавлении. Точка А — тройная точ­ка; В — критич. точка.


Зависимость темп-ры начала и окончания П. сплава от его состава при данном давлении изображается на диаграммах состоя­ния спец. линиями (кривые л и к в и д у с а и с о л и д у с а, рис. 2). У ряда высокомол. соединений (напр., в-в, способных образовывать жидкие



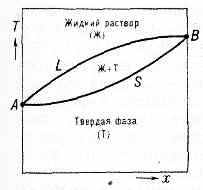
Рис. 2. Диаграм­ма состояния си­стемы (напр., Cu—Ni), образу­ющей непрерыв­ный ряд жидких и твёрдых раст­воров. Жидкий раствор устойчив выше линии лик­видуса L, твёр­дый — ниже ли­нии солидуса S; между линиями L и S заключена двухфазная область равновесия твёрдых и жидких фаз.

Т — темп-pa, х — состав раствора (относит. кол-во компоненты В в компоненте А).


кристаллы) переход из тв. крист. состояния в изотропное жидкое про­исходит постадийно (в нек-ром темпе­ратурном интервале), каждая стадия характеризует определённый этап разрушения крист. структуры.

Наличие определённой темп-ры П.— важный признак крист. строения тв. тел. По этому признаку их легко

отличить от аморфных тв. тел, к-рые не имеют фиксированной T_пл. Аморф­ные тв. тела переходят в жидкое со­стояние постепенно, размягчаясь при повышении темп-ры (см. Аморфное состояние).

Самую высокую темп-ру П. среди чистых металлов имеет вольфрам (3410°С), самую низкую — ртуть (-38,9°С). К особо тугоплавким со­единениям относятся TiN (3200°C), HfN (3580°C), ZrC (3805°C), ТаС (4070°С), HfC (4160°C) и др. Как пра­вило, для в-в с высокой Т_пл характер­ны более высокие значения L_пл. При­меси, присутствующие в крист. в-вах, снижают Т_пл. Этим пользуются на практике для получения сплавов с низкой Т_пл (напр., у т. н. сплава Вуда, состоящего из 50% Bi, 25% Pb, 12,5% Sn и 12,5% Cd, T_пл=68°С) и охлаждающих смесей [напр., смесь из льда (42,8%) и К₂СО₃ (57,2%) плавится при -46°С].




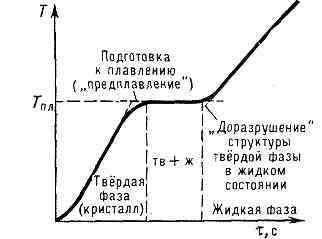
Рис. 3. Остановка изменения темп-ры при плавлении крист. тела. По оси абсцисс от­ложено время , пропорциональное равно­мерно подводимому к телу кол-ву теплоты.

П. начинается при достижении крист. в-вом Т_пл и протекает при пост. темп-ре (Т_пл), несмотря на сообщение в-ву теплоты (рис. 3).



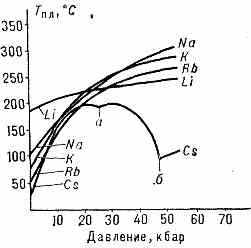
Рис. 4. Изменение темп-ры плавления Т_пл (°С) щелочных металлов с увеличением дав­ления р (кбар). Изломы на кривой плавле­ния Cs указывают на существование у него при высоких давлениях двух полиморфных превращений (а и б).


Нагреть кристалл до Т>Т_пл в обычных условиях не удаётся (см. Перегрев), тогда как при кристаллизации срав­нительно легко достигается значит. переохлаждение расплава.

Хар-р зависимости Т_пл от давления р определяется направлением объём­ных изменений (V_пл) при П. (см.

Клапейрона — Клаузиуса уравнение). В большинстве случаев П. в-в сопро­вождается увеличением их объёма (обычно на неск. %). Если это имеет место, то возрастание давления приво­дит к повышению Т_пл (рис. 4). Однако у нек-рых в-в (см. рис. 1) при П. происходит уменьшение объёма. Темп-ра П. этих в-в при увеличении давле­ния снижается.

П. сопровождается изменением физ. св-в в-ва: увеличением энтропии, что отражает разупорядочение крист. структуры; ростом теплоёмкости; электрич. сопротивления [исключение составляют нек-рые полуметаллы (Bi, Sb) и полупроводники (Ge), в жидком состоянии обладающие более высокой электропроводностью]. Практически до нуля падает при П. сопротивление сдвигу (в расплаве не могут распро­страняться поперечные упругие вол­ны), уменьшается скорость распростра­нения звука (продольных волн) и т. д.

Согласно мол.-кинетич. представле­ниям, П. осуществляется след. обра­зом. При подведении к крист. телу теплоты увеличивается энергия коле­баний (амплитуда колебаний) его ато­мов, что приводит к повышению темп-ры тела и способствует образованию в кристалле разл. дефектов (незапол­ненных узлов крист. решётки — вакан­сий, нарушений периодичности решёт­ки внедрившимися между её узлами атомами и др.; см. Дефекты в кристал­лах). В мол. кристаллах может про­исходить частичное разупорядо­чение взаимной ориентации осей моле­кул, если молекулы не обладают сферич. симметрией. Постепенный рост числа дефектов и их объединение ха­рактеризуют стадию предплавления. С достижением Т_пл в кристалле созда­ётся критич. концентрация дефектов, начинается П.— крист. решётка рас­падается на легкоподвижные субмикроскопич. области. Подводимая при П. теплота идёт не на нагрев тела, а на разрыв межатомных связей и разрушение дальнего порядка в кри­сталлах (см. Дальний и ближний поря­док). В самих же субмикроскопич. областях ближний порядок в располо­жении атомов при П. существенно не меняется (координационное число расплава при Т_пл в большинстве слу­чаев остаётся тем же, что и у кристал­ла). Этим объясняются меньшие значе­ния теплот плавления L_пл по сравне­нию с теплотами парообразования и сравнительно небольшое изменение ряда физ. свойств в-в при их П.

Процесс П. играет важную роль в природе (П. снега и льда на поверх­ности Земли, П. минералов в её нед­рах и т. д.), в науке и технике (про­изводство чистых металлов и сплавов, литьё в формы и др.).

• Френкель Я. И., Кинетическая тео­рия жидкостей, Собр. избр. трудов, т. 3, М.—Л., 1959; Данилов В. И., Строение и кристаллизация жидкости, К., 1956; У б-

535


б е л о д е А., Плавление и кристалличес­кая структура, пер. с англ., М., 1969; Л ю б о в Б. Я., Теория кристаллизации в боль­ших объемах, М., 1975.

Б. Я. Любое.

ПЛАЗМА, частично или полностью ионизованный газ, в котором плотно­сти положит. и отрицат. зарядов практически одинаковы. При силь­ном нагревании любое в-во испаряется, превращаясь в газ. Если увеличивать темп-ру и дальше, резко усилится процесс термич. ионизации, т. е. мо­лекулы газа начнут распадаться на составляющие их атомы, к-рые затем превращаются в ионы. Ионизация га­за, кроме того, может быть вызвана его вз-ствием с эл.-магн. излучением (фотоионизация) или бомбардировкой газа заряж. ч-цами.

Свободные заряж. ч-цы, особенно эл-ны, легко перемещаются под дейст­вием электрич. поля. Поэтому в состо­янии равновесия пространственные за­ряды входящих в состав П. отрицат. эл-нов и положит. ионов должны ком­пенсировать друг друга так, чтобы полное поле внутри П. было равно нулю. Именно отсюда вытекает необ­ходимость практически точного равен­ства плотностей эл-нов и ионов в П.— её «к в а з и н е й т р а л ь н о с т и». Нарушение квазинейтральности в объ­ёме, занимаемом П., ведёт к немедлен­ному появлению сильных электрич. полей пространств. зарядов, тут же восстанавливающих квазинейтраль­ность. С т е п е н ь ю и о н и з а ц и и П.  наз. отношение числа ионизован­ных атомов к полному их числу в еди­нице объёма П. Для многозарядных ионов следует учитывать кратность ионизации атомов. В зависимости от величины а говорят о слабо, сильно и полностью ионизованной П.

Средние энергии разл. типов ч-ц, составляющих П., могут отличаться одна от другой. В таком случае П. нельзя охарактеризовать одним значе­нием темп-ры Т, и различают элек­тронную темп-ру Т_е, ионную темп-ру T_i (или ионные темп-ры, если в П. имеются ионы неск. сортов) и темп-ру нейтр. атомов Т_а (нейтр. компоненты). Подобная П. наз. н е и з о т е р м и ч е с к о й, в то время как П., для к-рой темп-ры всех компонент равны, наз. изотермической.

Применительно к П. несколько не­обычный смысл (по сравнению с др. разделами физики) вкладывается в понятия «низкотемпературная» и «вы­сокотемпературная». Низкотемпера­турной принято считать П. с T_i10⁵ К, а высокотемпературной — П. с T_i10⁶—10⁸ К и более. Это условное разделение связано с особой важно­стью высокотемпературной П. в свя­зи с проблемой осуществления управ­ляемого термоядерного синтеза (УТС).

В состоянии П. находится подав­ляющая часть в-ва Вселенной — звёз­ды, звездные атмосферы, галактич туманности и межзвёздная среда. Око­ло Земли П. существует в космосе в виде солнечного ветра, заполняет маг­нитосферу Земли (образуя радиацион­ные пояса Земли) и ионосферу. Процес­сами в околоземной П. обусловлены магн. бури и полярные сияния. Отра­жение радиоволн от ионосферной П. обеспечивает возможность дальней радиосвязи на Земле.

В лаб. условиях и пром. примене­ниях П. образуется в электрическом разряде в газах (дуговом разряде, искро­вом разряде, тлеющем разряде и пр.), в процессах горения и взрыва, исполь­зуется в плазменных ускорителях, магнитогидродинамических генераторах, в установках для исследования УТС. Многими характерными для П. св-вами обладают совокупности эл-нов и дырок в полупроводниках и эл-нов про­водимости (нейтрализуемых неподвиж­ными положит. ионами) в металлах, к-рые поэтому наз. плазмой твёрдых тел. Её отличит. особенность — воз­можность существования при сверх­низких для «газовой» П. темп-pax — комнатной и ниже, вплоть до абс. нуля темп-ры.

Возможные значения плотности П. n расположены в очень широком диа­пазоне: от n~10^-6см^-3 в межгалактич. пространстве и n~10 в солнечном вет­ре до n~10²² для тв. тел и ещё больших значений в центр. областях звёзд.

Термин «П.» в физике был введён в 1929 амер. учёными И. Ленгмюром и Л. Тонксом, проводившими зондовые измерения параметров низкотем­пературной газоразрядной П. Кинетика П. рассматривалась в работах Л. Д. Ландау в 1936 и 1946 и А. А. Власова в 1938. В 1942 X. Альфвен предложил уравнения магнитной гидродинамики для объяснения ряда явлений в косм. П. В 1950 в СССР и США была пред­ложена идея магн. термоизоляции П. для осуществления УТС. В 50—80-е гг. 20 в. изучение П. стимулировалось разл. практич. применениями П., раз­витием астрофизики и космофизики (наблюдение косм. П. и объяснение процессов в ней) и физики верхней атмосферы Земли — особенно в связи с полётами косм. летат. аппаратов, а также интенсификацией исследований по проблеме УТС.

Основные свойства плазмы. В рез­ком отличии св-в П. от св-в нейтр. га­зов определяющую роль играют два фактора. Во-первых, вз-ствие ч-ц П. между собой характеризуется кулоновскими силами притяжения и отталки­вания, убывающими с расстоянием гораздо медленнее (т. е. значительно более «дальнодействующими»), чем си­лы вз-ствия нейтр. ч-ц. По этой при­чине вз-ствие ч-ц в П. является, строго говоря, не «парным», а «коллек­тивным» — одновременно взаимо­действует друг с другом большое чис­ло ч-ц. Во-вторых, электрич. и магн. поля очень сильно действуют на П., вызывая появление в П. объёмных за­рядов и токов и обусловливая целый

ряд специфич. св-в П. Эти отличия позволяют рассматривать П. как осо­бое, четвёртое состояние в-ва.

К важнейшим св-вам П. относится упомянутая выше квазинейтральность. Она соблюдается, если линейные раз­меры области, занимаемой П., много больше дебаевского радиуса экраниро­вания



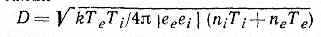
(е_е и e_i — заряды эл-нов и ионов, n_e и n_i — электронная и ионная плот­ности; здесь и ниже используется абс. система единиц Гаусса; см. СГС систе­ма единиц). Следовательно, лишь при выполнении этого условия можно го­ворить о П. как таковой. Электрич. поле отд. ч-цы в П. экранируется ч-цами противоположного знака, т. е. практически исчезает, на расстояниях порядка D от ч-цы. Величина D опреде­ляет и глубину проникновения внеш. электростатич. поля в П. Квазинейт­ральность может нарушаться вблизи поверхности П., где более быстрые эл-ны вылетают по инерции за счёт теплового движения на длину ~D (рис. 1).

П. наз. идеальной, если по­тенциальная энергия вз-ствия ч-ц мала по сравнению с их тепловой энергией. Это условие выполняется, когда число ч-ц в сфере радиуса D велико: N_D=⁴/₃ D³n>>1. В молнии T~2•10⁴ К,

n~2,5•10¹⁹ (плотность воздуха) и, сле­довательно, D~10^-7 см, но N_D~1/10.



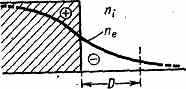
Рис. 1. Наруше­ние квазинейт­ральности плазмы на длине порядка дебаевского ра­диуса экраниро­вания D.


Такую П. наз. с л а б о н е и д е а л ь н о й.

Помимо хаотич. теплового движе­ния, ч-цы П. могут участвовать в упо­рядоченных «коллективных процес­сах», из к-рых наиболее характерны продольные колебания пространств. заряда, называемые л е н г м ю р о в с к и м и в о л н а м и. Их угловая частота (₀=(4nе²/m) наз. плазмен­ной частотой (e и m — заряд и масса эл-на). Многочисленность и разнооб­разие коллективных процессов, отли­чающие П. от нейтр. газа, обусловле­ны «дальностью» кулоновского вз-ствия ч-ц П., благодаря чему П. можно рассматривать как упругую среду, в к-рой легко возбуждаются и распро­страняются разл. шумы, колебания и волны.

В магн. поле с индукцией В на ч-цы П. действует Лоренца сила; в резуль­тате этого заряж. ч-цы П. вращаются с циклотронными частотами _B= еВ/mс по л а р м о р о в с к н м с п и р а л я м (кружкам) радиуса _B=v_/_b, где v_— перпендикуляр­ная B составляющая скорости ч-цы (подробнее см. Магнитные ловушки). В таком вз-ствии проявляется д и а-

536


м а г н е т и з м П.: создаваемые эл-нами и ионами круговые токи умень­шают внеш. магн. поле; при этом эл-ны вращаются по часовой стрелке, а ио­ны — против неё (рис. 2). Магн. мо­менты таких круговых токов равны =mv²/2B и в неоднородном поле на них действует (диамагнитная) сила, стремящаяся вытолкнуть ч-цу П. из области сильного поля в область более



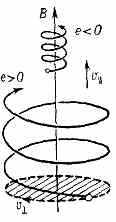
Рис. 2. Вращение ионов и эл-нов по ларморовским спиралям. Радиус враще­ния иона (е>0) больше радиуса вращения эл-на (е<0).


слабого поля, что является важнейшей причиной неустойчивости П. в неоднородных полях.

Взаимные столкновения ч-ц в П. описывают эфф. поперечными сечения­ми, характеризующими «площадь ми­шени», в к-рую нужно «попасть», чтобы произошло столкновение. Напр., эл-н, пролетающий мимо иона на расстоя­нии т. н. п р и ц е л ь н о г о п а р а м е т р а  (рис. 3), отклоняется си­лой кулоновского притяжения на угол , примерно равный отношению потенциальной энергии к кинетической, так что 2/, где =e²/mv²е²/kТ (здесь  — прицельное рас­стояние, при к-ром угол отклонения 0=90°).



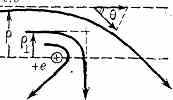
Рис. 3. Эл-н, про­летающий мимо ио­на, движется по ги­перболе.  — угол отклонения.


На большие углы ~1 рад рассеиваются все эл-ны, попадающие в круг с площадью _близ4², к-рую можно назвать сечением «близ­ких» столкновений. Если, однако, учесть и далёкие пролёты с >>, то эфф. сечение увеличивается на мно­житель =ln (D/), наз. к у л о н о в с к и м л о г а р и ф м о м. В пол­ностью ионизованной П. обычно ~10—15, и вкладом близких столкно­вений можно вообще пренебречь (см. сказанное выше о «дальнодействии» в П.). При далёких же пролётах ско­рости ч-ц изменяются на малые вели­чины, что позволяет рассматривать их движение как процесс диффузии в своеобразном «пространстве скоро­стей».

Если в П. не возбуждены к.-л. ин­тенсивные колебания и неустойчиво­сти, то именно столкновения ч-ц опре­деляют её т. н. диссипативные св-ва — электропроводность, вязкость, тепло­проводность и диффузию. В полностью ионизованной П. электропроводность

а не зависит от плотности П. и пропор­циональна T^3/2; при T~15•10⁶К она превосходит электропроводность се­ребра, поэтому часто, особенно при быстрых крупномасштабных движени­ях, П. можно приближённо рассматри­вать как идеальный проводник, пола­гая . Если такая П. движется в магн. поле, то эдс при обходе любого замкнутого контура, движущегося вместе с П., равна нулю, что по закону Фарадея для электромагнитной ин­дукции приводит к постоянству магн. потока, пронизывающего контур (рис. 4).



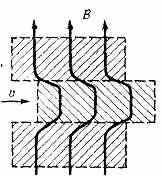
Рис. 4. Движение си­ловых линий магн. поля B вместе с плаз­мой (св-во вмороженности силовых ли­ний), в — скорость среды.


Эта «приклеенность», или в м о р о ж е н н о с т ь, м а г н и т н о г о п о л я также относится к важнейшим свойствам П. (подробнее см. в ст. Магнитная гидродинамика). Ею обусловлена, в частности, возмож­ность самовозбуждения (генерации) магн. поля за счёт увеличения длины магн. силовых линий при хаотич. тур­булентном движении среды. Напр., в косм. туманностях часто видна волок­нистая структура, свидетельствующая о наличии возбуждённого т. о. магн. поля.

Методы теоретического описания плазмы. Осн. методами являются: 1) исследование движения отд. ч-ц П.; 2) магнитогидродинамич. описание П.; 3) кинетич. рассмотрение ч-ц и волн в П. В разреженной П., где мож­но пренебречь столкновениями, заряж. ч-ца летит со скоростью v_║ вдоль магн. силовой линии, быстро вращаясь по ларморовской спирали (рис. 2). При наличии возмущающей силы F ч-ца также медленно «дрейфует» в направ­лении, перпендикулярном как магн. полю, так и направлению силы F. Напр., в электрич. поле Е, направлен­ном под углом к магнитному, проис­ходит «электрич. дрейф» со скоростью v_др.эл.=cE/B (E — составляющая напряжённости электрич. поля, пер­пендикулярная магн. полю В). Если же E=0, но магн. поле неоднородно, то имеет место «центробежный дрейф» в направлении бинормали к силовой линии, а в продольном направлении диамагнитная сила тормозит ч-цу, при­ближающуюся к области более силь­ного магн. поля. При этом остаются неизменными полная энергия ч-цы

(т/2)(v²_║+v²) и ее магн. момент =mv²/2B, являющийся адиабатич. ин­вариантом. Таково, напр., движение в магн. поле Земли косм. ч-ц (рис. 5), к-рые отражаются от полярных обла­стей, где поле сильнее, и вместе с тем

дрейфуют вокруг Земли (протоны — на запад, эл-ны — на восток). Поле Земли является м а г н и т н о й л о в у ш к о й: оно удерживает захваченные им ч-цы в радиац. поясах. Аналогич­ными св-вами удержания П. обладают т. н. з е р к а л ь н ы е магн. ловуш­ки, применяемые в исследованиях по УТС (подробнее см. Магнитные ло­вушки).



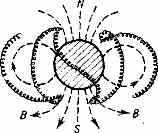
Рис. 5. Движение косм. ч-ц, захвачен­ных магн. полем Зем­ли.


При описании П. с помощью урав­нений магн. гидродинамики она рас­сматривается как сплошная среда, в к-рой могут протекать токи. Вз-ствие этих токов с магн. полем создаёт объ­ёмные электродинамич. силы, к-рые должны уравновешивать газодинамич. давление П., аналогичное давлению в нейтр. газе (см. Газовая динамика). В состоянии равновесия магн. силовые линии и линии тока должны прохо­дить по поверхностям пост. давления. Если поле не проникает в П. (модель «идеального» проводника), то такой поверхностью является сама граница П., и на ней газодинамич. давление П. p_газ должно быть равно внеш. магн. давлению р_магн=В²/8. На рис. 6 показан простейший пример та­кого равновесия — т. н. скинированный зет-пинч, возникающий при раз­ряде между двумя электродами.



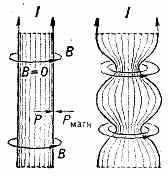
Рис. 6. Образование перетяжек на канале разряда, сжатого соб­ственным магн. полем: I — ток; В — индук­ция магн. поля, равная нулю внутри разряда.

Штри­ховка указывает линии тока на по­верхности П. Равновесие зет-пинча неустойчиво — на нём легко образу­ются желобки, идущие вдоль магн. поля. При последующем развитии они превращаются в тонкие перетяжки и могут приводить к обрыву тока (под­робнее см. Пинч-эффект). В мощных разрядах с токами ~10⁶ А в дейтериевой П. такой процесс сопровождается нек-рым числом ядерных реакций и ис­пусканием нейтронов, а также жёст­ких рентг. лучей, что впервые было об­наружено в 1952 Л. А. Арцимовичем, М. А. Леонтовичем и их сотрудника­ми.

Если внутри пинча создать про­дольное магн. поле В_║, то, двигаясь из-за вмороженности вместе с П., оно своим давлением будет препятст-

537


вовать развитию перетяжек. Желобки и в этом случае могут возникать вдоль винтовых силовых линий полного магн. поля, складывающегося из продоль­ного поля и поперечного поля B, к-рое создаётся самим током П. I_║ . Это имеет место, напр., в т. н. равновес­ном тороидальном пинче. Однако при условии B_║/B>R/a. (R и а — боль­шой и малый радиусы тора, рис. 7) шаг винтовых силовых линий полного поля оказывается больше длины замк­нутого плазменного шнура 2R, и желобковая неустойчивость, как пока­зывает опыт, не развивается. Такие системы, наз. токамаками, используются для исследований по проблеме УТС.



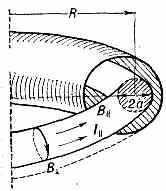
Рис. 7. Токамак. Токи, текущие в проводящем кожухе, препятствуют смещению плазменного шнура.


При рассмотрении движения П. методами магн. гидродинамики необ­ходимо учитывать степень вмороженности поля, определяемую магнит­ным числом Рейнольдса.

Наиболее детальным методом опи­сания П. является кинетический, ос­нованный на использовании функ­ции распределения ч-ц по координатам и импульсам f=f(t,r,p). Импульс ч-цы р равен mv. В состоянии термодинамического равновесия эта функция имеет вид универсального Максвелла распределения, а в общем случае её находят из кинетического уравнения Больцмана:



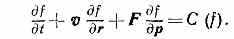
Здесь F=eE+(e/c)[vB] — внеш. сила, действующая на заряж. ч-цу П., а член С (f) учитывает взаимные столкно­вения ч-ц. При рассмотрении быстрых движений П. столкновениями часто можно пренебречь, полагая C(f)0. Тогда кинетич. ур-ние наз. б е с с т о л к н о в и т е л ь н ы м у р а в н е н и е м В л а с о в а с самосогла­сованными полями E и В (они сами определяются движением заряж. ч-ц). Если П. полностью ионизована, т. е. в ней присутствуют только заряж. ч-цы, то их столкновения, ввиду пре­обладающей роли далёких пролётов (см. выше), эквивалентны процессу диффузии в пространстве импульсов (скоростей). Выражение С(f) для такой П. было получено Л. Д. Ландау и может быть записано в виде:

C(f)=  (D•f--F_cf), где =д/др — градиент в импульс­ном пространстве, D — тензорный коэфф. диффузии в этом же пространст­ве, a F_c — сила взаимного (т. н. «ди­намического») трения ч-ц.

При высоких темп-pax и низкой плотности можно пренебречь столкно­вениями ч-ц с ч-цами в П. Однако в случае, когда в П. возбуждены волны к.-л. типа (см. ниже), необходимо учи­тывать «столкновения» ч-ц с волнами. При не слишком больших амплитудах колебаний в П. подобные «столкнове­ния», как и при далёких пролётах, со­провождаются малыми изменениями импульса ч-ц, и член С(f) сохраняет свой «диффузионный» вид с тем отли­чием, что коэфф. D определяется ин­тенсивностью волн. Важнейшим ре­зультатом кинетич. описания П. яв­ляется учёт вз-ствия волны с группой т. н. р е з о н а н с н ы х ч а с т и ц, скорости к-рых совпадают со скоро­стью распространения волны. Именно эти ч-цы могут наиболее эффективно обмениваться с волной энергией и им­пульсом. В 1946 Л. Д. Ландау пред­сказал возможность основанного на таком обмене «бесстолкновительного затухания» ленгмюровских волн, впо­следствии обнаруженного в опытах с П. Если направить в П. дополнит. пучок ч-ц, то подобный обмен может приводить не к затуханию, а к усиле­нию волн. Этот эффект в известном смысле аналогичен Черенкова — Вави­лова излучению.

Колебания и неустойчивости плазмы. Волны в П. отличают их объёмный ха­рактер и разнообразие св-в. С помощью разложения в ряд Фурье любое малое возмущение в П. можно представить



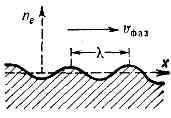
Рис. 8. Синусоидаль­ный профиль плотно­сти эл-нов в монохроматич. плазмен­ной волне.


как набор волн простейшего синусо­идального вида (рис. 8). Каждая такая (монохроматическая) вол­на характеризуется определённой час­тотой , длиной волны  и фазовой скоростью распространения v_ваз. Кро­ме того, волны могут различаться по­ляризацией, т. е. направлением век­тора электрич. поля в волне. Если это поле направлено вдоль скорости рас­пространения, волна наз. продоль­ной, а если поперёк — поперечной. В П. без магн. поля возможны волны трёх типов: продольные л е н г м ю р о в с к и е с частотой ₀, продоль­ные звуковые (точнее, и о н н о-з в у к о в ы е) и поперечные эл.-магн. (световые или радиоволны). Попереч­ные волны могут обладать двумя поля­ризациями и могут распространяться в П. без магн. поля, только если их частота со превышает плазменную час­тоту ₀. В противоположном же слу­чае <₀ показатель преломления П. становится мнимым, и поперечные вол­ны не могут распространяться внутри П., а отражаются её поверхностью

подобно тому, как лучи света отра­жаются зеркалом. Именно поэтому радиоволны с >~20 м отражаются ионосферой, что обеспечивает возмож­ность дальней радиосвязи на Земле.

Однако при наличии магн. поля по­перечные волны, резонируя с ионами и эл-нами на их циклотронных часто­тах, могут распространяться внутри П. и при <₀. Это означает появле­ние ещё двух типов волн в П., наз. а л ь ф в е н о в с к и м и и б ы с т р ы м и м а г н и т о з в у к о в ы м и. Альфвеновская волна представляет со­бой поперечное возмущение, распро­страняющееся вдоль магн. поля со скоростью v_A=B/(4nM_i) (М_i — мас­са ионов). Её природа обусловлена вмороженностью и упругостью сило­вых линий, к-рые, стремясь сократить свою длину и будучи «нагружены» ч-цами П., в частности массивными ионами, колеблются подобно натяну­тым струнам. Б ы с т р а я м а г н и т о з в у к о в а я волна в области малых частот по существу лишь поля­ризацией отличается от альфвеновской (их скорости близки и определяются магн. полем и инерцией тяжёлых ионов). В области же больших частот, где ионы можно считать неподвижны­ми, она определяется инерцией эл-нов и имеет специфич. винтовую поляри­зацию. Поэтому здесь её наз. «геликонной ветвью» колебаний, или «вет­вью вистлеров», т. е. свистов, по­скольку в магнитосферной П. она проявляется в виде характерных сви­стов при радиосвязи (см. Свистящие атмосферики). Кроме того, в П. может распространяться м е д л е н н а я м а г н и т о з в у к о в а я волна, к-рая представляет собой обычную звуковую волну с хар-ками, несколь­ко изменёнными магн. полем.

Т. о., при наличии магн. поля в од­нородной П. возможны волны шести типов: три высокочастотные и три низ­кочастотные. Если темп-pa или плот­ность П. в магн. поле неоднородны, то возникают ещё т. н. дрейфовые волны. При больших амплитудах воз­можны «бесстолкновительные» удар­ные волны (возбуждаемые, напр., на границе магнитосферы набегающим на Землю солнечным ветром), уединён­ные волны (солитоны), а также ряд др. «нелинейных» волн и, наконец, сильно развитая турбулентность дви­жения П.

В неравновесной П. при определён­ных условиях возможна «раскачка неустойчивостей», т. е. нарастание к.-л. из перечисленных типов волн до нек-рого уровня насыщения. Возмож­ны и более сложные случаи индуци­рованного возбуждения волн одного типа за счёт энергии волн др. типа.

Излучение плазмы. Спектр излуче­ния низкотемпературной (напр., газо­разрядной) П. состоит из отд. спектр. линий. В газосветных трубках, приме­няемых, в частности, для целей рек­ламы и освещения (лампы «дневного

538


света»), наряду с ионизацией происхо­дит и обратный процесс — рекомбина­ция ионов и эл-нов, дающая т. н. р е к о м б и н а ц и о н н о е и з л у ч е н и е со спектром в виде широких полос.

Для высокотемпературной П. со значит. степенью ионизации характер­но тормозное излучение с непрерыв­ным спектром, возникающее при столк­новениях эл-нов с ионами. В магн. поле ларморовское вращение эл-нов П. приводит к появлению т. н. м а г н и т о т о р м о з н о г о и з л у ч е н и я на гармониках циклотронной частоты, особенно существенного при больших (релятивистских) энергиях эл-нов. Важную роль в косм. П. играет вынужденное излучение типа обрат­ного Комптона эффекта. Им, а так­же магнитотормозным механизмом, обусловлено излучение нек-рых косм. туманностей, напр. Крабовидной.

К о р п у с к у л я р н ы м и з л у ч е н и е м П. наз. быстрые ч-цы, вы­летающие из неравновесной П. в ре­зультате развития разл. типов неустойчивостей. В первую очередь в П. раскачиваются к.-л. характерные ко­лебания, энергия к-рых затем переда­ётся небольшой группе «резонансных» ч-ц (см. выше). По-видимому, этим механизмом объясняется ускорение ма­лоэнергичных косм. ч-ц в атмосфере Солнца и в туманностях, образующих­ся при вспышках сверхновых звёзд типа пульсара в Крабовидной туман­ности.

Диагностика плазмы. Помещая в П. электрич. зонд (маленький электрод) и регистрируя зависимость тока от подаваемого напряжения, - можно оп­ределить темп-ру и плотность П. С по­мощью миниатюрной индукц. катуш­ки — «магн. зонда» — можно изме­рять изменение магн. поля во времени. Эти способы связаны, однако, с ак­тивным вмешательством в П. и могут внести нежелат. загрязнения. К более чистым методам относится «просвечи­вание» П. пучками нейтр. ч-ц и пуч­ками радиоволн. Лазерное просвечи­вание П. в разл. вариантах, в т. ч. с использованием голографии, являет­ся наиболее тонким и к тому же ло­кальным методом лабораторной диагностики П.

Часто используют также пассивные методы диагностики — наблюдение спектра излучения П. (единств. метод в астрономии), вывод быстрых нейтр. атомов, образовавшихся в результате перезарядки ионов в П., измерение уровня радиошумов. Плотную П. изу­чают с помощью сверхскоростной ки­носъёмки (неск. млн. кадров в с) и развёртки оптической. В исследова­ниях по УТС регистрируется также рентг. спектр тормозного излучения и нейтронное излучение дейтериевой П. (см. также Диагностика плазмы).

Применение плазмы. Высокотемпе­ратурная П. (Т~10⁸ К) из дейтерия и трития — осн. объект исследований по УТС. Такая П. создаётся путём

нагрева и быстрого сжатия П. током (используется также высокочастотный подогрев) либо путём инжекции высо­коэнергичных нейтр. атомов в магн. поле, где они ионизуются, либо облу­чением мишени мощными лазерами или р е л я т и в и с т с к и м и э л е к т р о н н ы м и п у ч к а м и.

Низкотемпературная П. (Т~10³ К) находит применение в газоразрядных источниках света и в газовых лазерах, в термоэлектронных преобразователях тепловой энергии в электрич. и в магнитогидродинамических генераторах (МГД-генераторах), где струя П. тор­мозится в канале с поперечным магн. полем В, что приводит к появлению



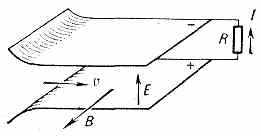
Рис. 9. Схема МГД-генератора, преобразую­щего кинетич. энергию движущейся плазмы в электрич. энергию. R — внеш. нагрузка генератора, по к-рой протекает ток I.


между верхним и нижним электродами (рис. 9) электрич. поля напряжён­ностью Е порядка Bv/c (v — скорость потока П.); напряжение с электродов подаётся во внеш. цепь.

Если «обратить» МГД-генератор, пропуская через П. в магн. поле ток от внеш. источника, образуется плаз­менный двигатель, весьма перспек­тивный для длит. косм. полётов.

Плазмотроны, создающие струи плотной низкотемпературной П., ши­роко применяются в разл. областях техники. В частности, с их помощью режут и сваривают металлы, наносят покрытия. В плазмохимии низкотем­пературную П. используют для полу­чения нек-рых хим. соединений, напр. галогенидов инертных газов, к-рые не удаётся получить др. путём. Кроме того, высокие темп-ры П. приводят к высокой скорости протекания хим. реакций — как прямых реакций син­теза, так и обратных реакций разло­жения. Если производить синтез «на пролёте» плазменной струи, расширяя и тем самым быстро охлаждая её на след. участке (такая операция наз. «закалкой»), то можно затруднить обратные реакции разложения и су­щественно повысить выход требуемого продукта.

•Арцимович Л. А., Элементарная физика плазмы, 3 изд., М., 1969; его же, Управляемые термоядерные реакции, 2 изд., М., 1963; Франк-Каменецкий Д. А., Лекции по физике плазмы, 2 изд., М., 1968; Альвен Г., Фельтхаммар К.-Г., Космическая электродинамика, пер. с англ., 2 изд., М., 1987; С п и т ц е р Л., Физика полностью ионизованного газа, пер. с англ., М., 1965; Гинзбург В. Л., Распространение электромагнитных волн в плазме, 2 изд., М., 1967; Трубни­ков Б. А., Введение в теорию плазмы, ч. 1—3, М., 1969—78: Вопросы теории плаз­мы. Сб., под ред. М. А. Леонтовича, в. 1 —10, М., 1963—80.

Б. А. Трубников.

ПЛАЗМА ТВЁРДЫХ ТЕЛ, условный термин, означающий совокупность подвижных заряженных ч-ц в тв. про­водниках (эл-нов проводимости в ме­таллах или эл-нов и дырок в полупроводниках) в таких условиях, когда их св-ва близки к св-вам газоразряд­ной плазмы. Это позволяет перенести представления, созданные при иссле­довании газоразрядной плазмы, в фи­зику тв. тела. П. т. т., в отличие от газоразрядной плазмы, имеет боль­шую плотность n заряженных ч-ц (в газоразрядной плазме n~10¹² см^-3, в металлах n~10²²—10²³ см^-3, в полупроводниках n~10¹⁵—10¹⁷ см^-3). Это приводит к различию хар-к П. т. т. и плазмы газового разряда. Напр., плазменная частота, пропор­циональная n, для П. т. т. сущест­венно больше, чем для газоразряд­ной плазмы. Плазменные эффекты в П. т. т. (особенно в полупровод­никах) используются для создания приборов СВЧ.

• Бауэрс Р., Плазма в твердых телах, в кн.: Физика твердого тела. Электронные свойства твердых тел, пер. с англ., М., 1972 (Над чем думают физики, в. 8); П л а т ц м а н Ф., В о л ь ф П., Волны и взаимодей­ствия в плазме твердого тела, пер. с англ., М., 1975. См. также лит. при ст. Твёрдое тело. М. И. Каганов.

ПЛАЗМЕННАЯ ЧАСТОТА, см. Ленгмюровские волны, Плазма.

ПЛАЗМЕННЫЕ ДВИГАТЕЛИ, ра­кетные двигатели, в к-рых рабочее тело ускоряется, находясь в состоя­нии плазмы. Скорости истечения рабо­чего тела, достижимые в П. д., сущест­венно выше скоростей, предельных для обычных газодинамич. (хим. или теп­ловых) двигателей. Увеличение ско­рости истечения позволяет получать данную тягу при меньшем расходе рабочего тела, что облегчает вес ра­кетной системы.

Практич. применение на сов. и амер. косм. летат. аппаратах нашли плаз­менные электрореактивные двигатели. В таких П. д. через рабочее тело про­пускается электрич. ток от бортового источника энергии, в результате чего образуется плазма с темп-рой в десят­ки тыс. градусов. Эта плазма затем ускоряется либо газодинамически, ли­бо за счёт силы Ампера, возни­кающей при вз-ствии протекающего по плазме тока с магн. полями (см. Плазменные ускорители).

Исследуются возможности создания П. д. на др. принципах. Так, сущест­вуют модели П. д., работающие на отдаче, вызванной разлётом продук­тов разложения и испарения поверх­ностей тв. тел, облучаемых мощными импульсами лазерного излучения или импульсными электронными пучками. Обсуждается также схема яд. ракет­ного двигателя на основе ядерного реактора с газофазными (точнее, плаз­менными) тепловыделяющими элемен­тами. В этом реакторе делящееся в-во должно находиться в состоянии плаз­мы с темп-рой в неск. десятков тыс.

539


градусов. При контакте с ним рабочее тело (напр., водород) будет нагревать­ся до соответствующих темп-р, что позволит получить скорости истечения в неск. десятков км/с.

• См. лит. при ст. Плазменные ускори­тели.

А. И. Морозов.

ПЛАЗМЕННЫЕ ИСТОЧНИКИ ЭЛЕК­ТРИЧЕСКОЙ ЭНЕРГИИ, преобразо­ватели тепловой энергии плазмы в электрич. энергию. Существуют два типа П. и. э. э.— магнитогидродинамический генератор и термоэлектрон­ный преобразователь.

ПЛАЗМЕННЫЕ НЕУСТОЙЧИВО­СТИ, самопроизвольное нарастание от­клонений от невозмущённого квази­стационарного состояния плазмы (со­стояния равновесия, стационарного течения и т. п.). П. н. связаны либо с пространств. неоднородностью плаз­мы, либо с неравновесностыо распре­деления по скоростям.

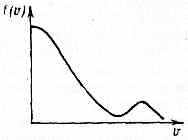
С знергетич. точки зрения для воз­никновения П. н. необходим нек-рый избыток свободной энергии (над тер­модинамически равновесной) в невоз­мущённом состоянии плазмы. В зави­симости от того, в какой форме энергии (магн., механич., тепловой) образуется избыток свободной энергии и в каком виде этот избыток высвобождается, различают разного вида П. н.: пучко­вые, магннтогидродинамич., дрейфо­вые, бесстолкновительные, параметрич., диссипативные, разрывные и т. д. Так, напр., если в разреженных плазмах невозмущённое состояние ионов и эл-нов плазмы описывается в виде суммы Максвелла распределения и дополнит. пучка ионов или эл-нов, движущегося со скоростью, пре­вышающей нек-­рое критич. зна­чение (см. рис.), то в плазме воз­никают т.н. п у ч к о в ы е неустой­чивости, к-рые приводят к самопроизвольному нарас­танию ленгмюровских волн с фазовыми скоростями, несколько меньшими ско­рости пучка. Анизотропия функций распределения ч-ц плазмы в простран­стве скоростей является также причи­ной анизотропных П. н. В плазме, помещённой в магн. поле, такие П. н. приводят к росту магнитоупругих колебаний (альфвеновские волны). Равновесные магнитогидродинамич. конфигурации могут обладать избытком свободной энергии в форме энергии магн. поля и энергии тепло­вого расширения плазмы. Это т. н. к о н ф и г у р а ц и о н н ы й избы­ток свободной энергии. Высвобожде­ние избытка энергии магн. поля при перестройке конфигурации явл. источ­ником наиболее быстро развивающей­ся разновидности м а г н и т о г и д р о д и н а м и ч е с к о й П. н. Примером может служить неустойчивость плазменного шнура, сжатого магн. полем, протекающего по нему тока, т. н. т о к о в а я П. н. (наблюдается при пинч-эффекте).



Наиболее ради­кальным методом стабилизации кон­фигураций подобного типа явл. на­ложение достаточно сильного продоль­ного магн. поля: H_║>H__║/2r (где H_ — магн. поле собств. тока; r — радиус плазменного шнура, _║ — про­дольная длина волны возмущения). Высвобождение конфигурац. избытка энергии при тепловом расширении плазмы связано с ж е л о б к о в ы м и П. н., к-рые представляют собой возмущения в виде вытянутых вдоль силовых линий магн. поля языков, расширяющихся поперёк силовых ли­ний в сторону ослабевающего магн. поля. Возмущения такого типа при­обретают характер перестановок целых элем. силовых трубок магн. поля, за­полненных плазмой. Желобковая П. н. явл. магнитогидродинамич. аналогом конвективной неустойчивости в обыч­ной гидродинамике.

Поскольку плазма, как сплошная среда, представляет собой систему с бесконечным числом степеней свободы, полный теор. анализ её устойчивости по отношению к разным видам возму­щений практически неосуществим. Об­щепринятый подход в физике устой­чивости плазмы состоит в последоват. рассмотрении разл. П. н., начиная с самых простых моделей — гидроди­намических, с постепенным усложне­нием (вводя в рассмотрение эффекты конечной диссипации, многокомпонентность плазмы, кинетич. эффекты и т. п.).

Наиболее исследованы П. н. отно­сительно малых возмущений, описы­ваемые в теории плазмы линейными уравнениями. В задачах о П. н. равно­весных магнитогидродинамич. конфи­гураций линеаризованные ур-ния тео­рии устойчивости идеально проводя­щей плазмы можно привести к одному уравнению движения



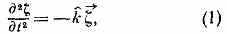
в к-ром k — нек-рый линейный само­сопряжённый дифф. оператор, действующий на ξ^ — смещение плазмы от равновесия, как на .функцию коорди­нат. Уравнение (1) аналогично ур-нию, описывающему колебания произволь­ной неоднородной упругой среды, где К играет роль соответствующего обоб­щённого коэфф. упругости. По ана­логии с механикой упругих сред вво­дится потенциальная энергия малых колебаний



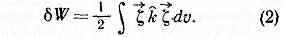
Если при всех смещениях ξ^ (r^) энергия системы увеличивается (W>0), то система находится в устойчивом со­стоянии с наименьшей потенциальной энергией, и все отклонения от положе­ния равновесия не могут нарастать во

времени. Если же W может прини­мать отрицат. значения, т. е. при нек-ром смещении система может пе­рейти в состояние с меньшей потенци­альной энергией, то рассматриваемая система неустойчива. Границу между устойчивыми и неустойчивыми конфи­гурациями образуют такие состояния, в к-рых исчезает упругость по отноше­нию к одному определённому типу смещений. Для нахождения границы устойчивости обычно исследуют, при каких условиях появляются состоя­ния, близкие к равновесному, с помощью уравнения kξ^=0, т. е. соответ­ствующие нулевым собственным час­тотам (т. н. безразличные равнове­сия). В линейной теории П. н. стацио­нарных состояний нарастание флукту­ации во времени носит экспоненци­альный характер ~exp(vt). Здесь v — т. н. и н к р е м е н т н е у с т о й ч и в о с т и — величина, характеризую­щая степень неустойчивости системы, быстроту возбуждения в ней колеба­ний. Порядок величины инкремента самых быстрых магнитогидродинамич. неустойчивостей ~vlr, где r — харак­терный пространств. размер конфигу­рации, v — характерная скорость (альфвеновская либо скорость звука в зависимости от типа неустойчиво­сти).

Часто состояния плазмы (равновес­ные конфигурации или течения), заве­домо устойчивые в рамках идеального гидродинамич. рассмотрения, при учё­те диссипативных эффектов (конечного электрич. сопротивления, вязкости и т. д.) оказываются неустойчивыми (т. н. диссипативные П. н.). Учёт неидеальности плазмы приводит к существенному снижению порога возникновения П. н. магнитогидроди­намич. конфигураций и течений. Дис­сипативные П. н. характеризуются су­щественно меньшими инкрементами и имеют характер более «медленного просачивания» (тем медленнее, чем меньше электрич. сопротивление) по сравнению с бурной перестройкой ис­ходной конфигурации при неустойчи­вости идеальной плазмы. Аналогом дис­сипативных П. н. в обычной гидроди­намике явл. неустойчивость течения Пуазёйля. При наличии магн. поля новым важным типом указанных П. н. явл. р а з р ы в н ы е, сопровождаю­щиеся изменением топологии магн. поля (разрыв и пересоединение сило­вых линий). Многокомпонентность плазмы также приводит к дополнитель­ным П. н., наиболее важным среди к-рых явл. дрейфовые. Как прави­ло, их характерные инкременты при­мерно в r/r_H раз меньше идеальных магнитогидродинамических (r_H — средний ларморовский радиус ионов плазмы).

Ответ на кардинальный вопрос — о конечной судьбе состояния плазмы в результате развития П. н. выходит за рамки линейной теории П. н. Как пра­вило, учёт нелинейных эффектов оста­навливает первоначально экспонен-

540


циальный рост П. н. на уровне «насы­щения». Универсального подхода для описания состояния насыщения П. н. не существует. В ряде случаев разра­ботаны приближённые нелинейные мо­дели. Как правило, П. н. исходных со­стояний, лежащих далеко за порогом неустойчивости, приводят к турбулент­ному состоянию насыщения. Так, напр., пучковые П. н. могут приво­дить к состоянию турбулентности плазменных волн.

Если П. н. дополнительно дестаби­лизируются нелинейными эффектами, то скорость нарастания таких П. н. увеличивается с ростом амплитуды возмущения (до нек-рого предела) — это т. н. в з р ы в н ы е неустойчиво­сти, примеры к-рых встречаются в за­дачах о нескольких взаимодействую­щих волнах.

Прогресс в изучении П. н. в значи­тельной степени был связан с работами по проблеме управляемого термоядер­ного синтеза, в результате чего уда­лось реализовать практически устой­чивые конфпгурацин горячей плазмы в магн. поле (см. Токамак).

П. н. анизотропного типа обнаруже­ны в магнитосфере Земли. Они играют важную роль в динамике радиацион­ных поясов, ч-цы к-рых представляют собой анизотропную в магн. поле ком­поненту плазмы.

Пучковые П. н., сопровождающие­ся генерацией ленгмюровскпх колеба­ний, представляют интерес для плаз­менной электроники, а в проблеме управляемого термоядерного синтеза используются в методах нагрева плаз­мы, основанных на пнжекции пучков заряженных ч-ц.

П. н. разрывного типа привлекают­ся для построения моделей пересоединения магн. поля в процессе эволюции конфигурации плазмы в токамаке и в нек-рых задачах астрофизики (пере­соединение магн. поля как источник энергии солнечных хромосферных вспышек).

• А р ц и м о в и ч Л. А., С а г д е е в Р. 3., Физика плазмы для физиков, М., 1979;

М и х а й л о в с к и й А. Б., Теория плазмен­ных неустойчивостей, 2 изд., т. 1—2, М., 1975—77.

Р. З. Сагдеев,

ПЛАЗМЕННЫЕ УСКОРИТЕЛИ, устройства для получения потоков плазмы со скоростями 10—10³ км/с, что соответствует кинетич. энергии ионов от ~10 эВ до 10⁵—10⁷ эВ. На нижнем пределе энергии П. у. соседствуют с генераторами низкотемпературной плазмы -- плазмотронами, на верх­нем — с коллективными ускорителями заряженных ч-ц (см. Коллективные методы ускорения).

Плазменные потоки с большими ско­ростями можно получить разными способами, напр, воздействием лазер­ного излучения на тв. тело. Однако доведены до определённого уровня со­вершенства и получили широкое рас­пространение только те П. у. (рис. 1), в к-рых ускорение и создание плазмы осуществляется за счёт электрич. энер­гии с помощью электрич. разрядов.

В отличие от ускорителей заряжен­ных ч-ц, в канале П. у. находятся од­новременно ч-цы с зарядами обоих знаков — положит. ионы и эл-ны, т. е. не нарушается квазинейтраль­ность плазмы. Это снимает ограниче­ния, связанные с пространственным зарядом (см. также Ленгмюра форму­ла), и позволяет, напр., получать квазистационарные (т. е. длитель­ностью 10 ^-2—10^-3 с) плазменные потоки с эфф. током ионов порядка млн. А при энергии ч-ц ~100 эВ.



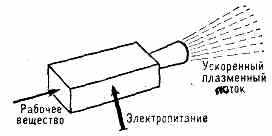
Рис. 1. Принципиальная схема плазменного ускорителя.