П падение тела

Вид материала

Документы

Содержание Перезарядка ионов Перезарядки реакция Рис. 1. Одинарный тандем: И — источник отрицат. ионов; Г — высоковольтный гене­ратор; В — высоковольтный электрод; М — перезаряд Переключения эффект В. В. Сандомирский, А. А. Суханов. Комптона эффект А. В. Ефремов. Переменный ток Рис. 1. График периодич. перем. то­ка i(t). Рис. 3. Схема цепи и графики напряжения и u тока i в цепи, содержащей только актив­ное сопротивление r. С заряд на его обкладках будет равен q=Cu. Рис. 5. Схема цепи и графики напряжения u и тока i в цепи, содержащей только ём­кость С. Кирхгофа правила. А. С. Касаткин. Е. Ур-ние (2) явл. основным ур-нием ренормализац. группы. Оно говорит о том, что изме­нение эфф. заряда Е (т*) А. В. Ефремов.

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПЕРЕЗАРЯДКА ИОНОВ, взаимодей­ствие положит. ионов с нейтр. атомами (молекулами) или поверхностью тв.

тела, сопровождающееся обменом эл-нами между взаимодействующими ч-цами. П. п. в газах и жидкостях происходит по схеме А⁺+В°+А°+В⁺ (верхние индексы указывают за­ряд ч-цы). Если при П. и. внутр. энергия системы взаимодействующих ч-ц не меняется, П. и. наз. резо­нансной. Таким процессом явл., напр., обмен эл-ном между атомарным ионом и атомом того же элемента (или между мол. ионом и молекулой того же в-ва). Вероятность П. и., определяе­мая её эфф. поперечным сечением, зависит от рода ч-ц А и В и скорости их относит. движения, а также от параметра aE/hv (a — размер иони­зуемой ч-цы, Е — изменение внутр. энергии, v — относит. скорость ч-ц). При уменьшении v сечение П. п. силь­но уменьшается для нерезонансной П. и. (когда aE/hv>> 1) и монотонно



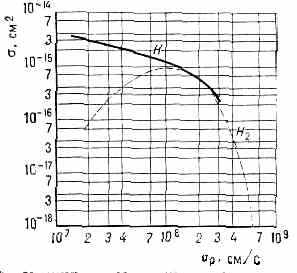
Эфф. сечения перезарядки ионов водорода (протонов) в атомном (резонансная переза­рядка) и молекулярном (нерезонансная пере­зарядка) водороде; v — относит. скорости сталкивающихся ч-ц.


возрастает для резонансной. Типичный пример — перезарядка протонов на атомарном и мол. водороде (рис.). Процессы П. и. могут играть существ. роль в балансе ч-ц высокотемператур­ной плазмы.

Возможна также резонансная П. и. с образованием нейтр. атома (молеку­лы) не в основном состоянии, а в возбуждённом состоянии, когда эл-н захватывается на один из свободных верхних уровней энергии.

П. и. вблизи поверхности металла (с захватом эл-на ионом из металла) происходит аналогично П. и. в газах. Особый вид П. и.— захват двух эл-нов с образованием отрицат. иона — возможен для положит. атомарных или мол. ионов газов, для к-рых ха­рактерно сродство к электрону.

Осн. роль в механизме П. и. играет туннельный эффект. П. и. широко используется в разл. вариантах ак­тивной и пассивной диагностики плазмы. См. также Ионизация, Стол­кновения атомные.

• См. лит. при ст. Ионизация.

ПЕРЕЗАРЯДКИ РЕАКЦИЯ, ядер­ная реакция типа (p, n), (n, p), (⁺ , °), (^-, °) и др.

ПЕРЕЗАРЯДНЫЙ УСКОРИТЕЛЬ (тандем), высоковольтный ускоритель, в к-ром благодаря перезарядке уско-

524


ряемых ч-ц (изменению знака, а иногда и величины заряда) одно и то же ускоряющее напряжение исполь­зуется дважды: отрицат. ионы уско­ряются при движении к положительно заряженному высоковольтному элект­роду В, а положит. ионы, образовав­шиеся после перезарядки,— при дви­жении от него (рис. 1). Образующиеся после перезарядки ч-цы с различным



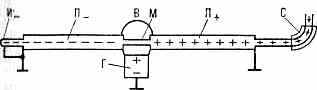
Рис. 1. Одинарный тандем: И — источник отрицат. ионов; Г — высоковольтный гене­ратор; В — высоковольтный электрод; М — перезарядная мишень; П_- — пучок отрицат. ионов; П₊ — пучок положит. ионов; С — сепаратор.


Z₊ ускоряются до разных энергий, поэтому для их разделения после ускорения требуется сепаратор — магнит с полем, перпендикулярным направлению движения ч-ц (см. Масс-спектрометр). Энергия ч-ц на выходе П. у. равна ξ=eu(Z₊+Z_-), где u — напряжение высоковольтного гене­ратора, a Z_- и Z₊ — числа элемен­тарных зарядов ч-цы до и после пере­зарядки (обычно Z_-=l). Дополнит. преимущество П. у.— нулевой потен­циал ионного источника. Добавление ещё одного генератора противопо­ложной полярности (двойной тан­дем, рис. 2) позволяет повысить энер­гию ч-ц до величины ξ=eu(Z₊+2Z_-).



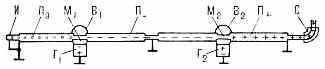
Рис. 2. Двойной тандем: И — источник нейтр. ч-ц; П₀ — пучок нейтр. ч-ц; Г₁ — высоковольтный генератор первого ускори­теля, B₁ — его высоковольтный электрод; Г₂ — генератор второго ускорителя; В₂ — второй высоковольтный электрод; M₁ и М₂ — перезарядные мишени; П_- — пучок от­рицат. ионов; П₊ — пучок положит. ионов; С — сепаратор.


Типичная энергия протонов, ускоряе­мых в П. у. ξ ~ 10— 20 МэВ.

Идея использовать перезарядку для увеличения энергии ускоряемых ч-ц предложена У. X. Беннеттом (США) в 1935. Она была реализована лишь в 1958, после разработки эфф. источни­ков отрицат. ионов и перезарядных мишеней — газовых и твёрдых (от­рицат. ионы могут быть получены непосредственно из источника или перезарядкой положит. ионов на га­зовой или пароструйной мишени, пе­резарядкой при взаимодействии пуч­ка с твёрдой поверхностью, покрытой атомами щелочных металлов, и т. д.).

•Комар Е. Г., Основы ускорительной техники, М., 1975.

М. П. Свиньин.

ПЕРЕКЛЮЧЕНИЯ ЭФФЕКТ, скач­кообразный и обратимый переход полу­проводника из высокоомного состояния в низкоомное под действием электрич.

поля Е, превышающего пороговое E_п=10⁴—10⁶ В/см. П. э. наблюда­ются в однородных ПП с S-образной вольтамперной характеристикой. При подаче на ПП прямоуг. импульса напряжения U_п, создающего электрич. поле, переход в низкоомное состоя­ние начинается через время ~10^-6—10^-8 с (время задержки), к-рое тем меньше, чем больше перенапряжение (U-U_п). Время самого скачка ~10^-10 с. П. э. наз. моностаби­льным, если для поддержания низкоомного состояния необходимо не­прерывно пропускать через ПП доста­точно большой ток, и бистабильным (с памятью), если низкоомное состояние после отключения постоян­ного напряжения легко восстанавли­вается при пропускании через ПП короткого и мощного импульса тока. П. э. ярко выражен у аморфных полупроводников, в частности у стек­лообразных (к к-рым относятся при­ведённые хар-ки), хотя наблюдается и у нек-рых кристаллич. полупровод­ников. В массивных слоях стёкол толщиной > 10 мкм П. э. обусловлен джоулевым разогревом. В тонких плён­ках природа П. э. обычно объясняется электротепловой неустойчивостью. В низкоомном состоянии ток течёт в узком канале (шнуре). «Запоминание» при бистабильном П. э. обусловлено кристаллизацией стекла в токовом шнуре, а в нек-рых случаях — проник­новением атомов металла (с электро­дов) в ПП. Наибольшее применение находит бистабильный П. э. для создания элементов памяти. Моноста­бильный П. э. используется гл. обр. в логич. схемах. Перспективность использования П. э. в стёклах свя­зана с их радиац. стойкостью.

• Мотт Н., Дэвис Э., Электронные процессы в некристаллических веществах, пер. с англ., М., 1974; Сандомирекий В. Б., Суханов А. А., Явления электрической неустойчивости (переключе­ние) в стеклообразных полупроводниках, «Зарубежная радиоэлектроника», 1976, № 9, с. 68.

В. В. Сандомирский, А. А. Суханов.

ПЕРЕКРЕСТНАЯ СИММЕТРИЯ (кроссинг-симметрия), в квантовой те­ории поля (КТП) особая симметрия, связывающая амплитуду рождения к.-л. ч-цы с амплитудой поглоще­ния соответствующей античастицы. В основе П. с. лежат два положения: 1) инвариантность ур-ний КТП отно­сительно преобразований СРТ, т. е. относительно замены ч-цы на антича­стицу с противоположным по знаку импульсом и энергией (см. Теорема СРТ); 2) аналитич. св-ва амплитуд; амплитуда любого процесса явл. аналитич. ф-цией переменных s_ij=ξ_iξ_j-p_ip_j, где ξ_i(ξ_j) и p_i(p_j) — энергия и импульс ч-цы i(j). П. с. означает, напр., что три процесса: a+bc+d (I), a+d^~c+b^~ (II), a+c^~b^~+d (III) описываются одной и той же аналитич. ф-цией переменных s_ab, s_ac и s_ad, но в разных областях их изменения. Так, если ч-цы а и с — -кванты,

a b и d — эл-ны, то процессами I, II, III в соответствующих областях .будут: +e^-+e^-,+е⁺+е⁺ — Комптона эффект на эл-не и позитроне; +е⁺+е^- — рожде­ние фотонами пары электрон-позитрон (или е⁺+е- + — её двухфотонная аннигиляция).

П. с. явл. неотъемлемой составной частью метода дисперсионных соот­ношений и Редже полюсов метода.

А. В. Ефремов.

ПЕРЕМАГНИЧИВАНИЕ, изменение направления намагниченности ферро- или ферримагнитного образца на про­тивоположное под действием внешнего магн. поля (подробнее см. Гистерезис, Намагничивание).

ПЕРЕМЕННЫЙ ТОК, в широком смысле электрический ток, изменяю­щийся во времени. П. т. создаётся перем. напряжением. В технике обычно под П. т. понимают периодич, ток, в к-ром средние за период значе­ния силы тока и напряжения равны нулю. Периодом Т П. т. наз. наи­меньший промежуток времени (в с), через к-рый значения силы тока (и напряжения) повторяются (рис. 1). Важной хар-кой П. т. явл. его частота



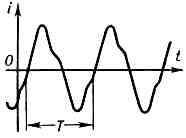
Рис. 1. График периодич. перем. то­ка i(t).


f — число периодов в 1 с: f=1/T. В СССР стандартная техн. частота f=50 Гц.

Для передачи и распределения элек­трич. энергии преим. используется П. т. (благодаря простоте трансфор­мации его напряжения почти без по­терь мощности). П. т. может быть выпрямлен, напр. ПП выпрямителем, а затем с помощью ПП инверторов преобразован вновь в П. т. другой, регулируемой частоты; это создаёт возможность использовать простые и дешёвые двигатели П. т. (асинхрон­ные и синхронные) для электроприво­дов, требующих плавного регулиро­вания скорости. Генераторы и дви­гатели П. т. по сравнению с машинами постоянного тока при равной мощно­сти проще по устройству, дешевле и надёжнее.

Для хар-ки силы П. т. за основу принято сопоставление ср. теплового действия П. т. с тепловым действием пост. тока соответствующей силы. Полученное таким путём значение си­лы I П. т. наз. действующим (или эффективным) значением, математически представляющим сред­неквадратичное за период значение силы тока. Аналогично определяется и действующее значение напряжения U П. т. Амперметры и вольтметры

525


П. т. измеряют именно действующие значения тока и напряжения.

В простейшем и наиб. важном слу­чае мгновенное значение силы i П. т. меняется во времени t по синусоидаль­ному закону: i=I_msin(t+), где I_m— амплитуда тока, =2f — его круго­вая частота,  — нач. фаза. Синусо­идальный (гармонический) ток созда­ётся синусоидальным напряжением u той же частоты: u=U_msin(t+),



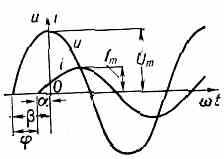
Рис. 2. Графики напряжения u и тока i в цепи перем. тока при сдвиге фаз .


где U_m— амплитуда напряжения, — нач. фаза (рис. 2). Действующие зна­чения такого П. т. равны: I=I_m20,707 1_m, U=U_т/20,707U_m. Для синусоидальных токов, удовлет­воряющих условиям квазистационар­ности (см. Квазистационарный ток; в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифф. форме спра­ведлив и для неквазистационарных токов в линейных цепях). Из-за нали­чия в цепи П. т. индуктивности L или (и) ёмкости С между током i и напряжением и в общем случае возни­кает сдвиг фаз =-, зависящий от параметров цепи (r, L, С, где r — активное сопротивление) и частоты .



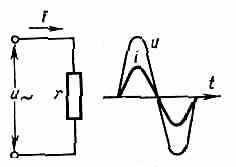
Рис. 3. Схема цепи и графики напряжения и u тока i в цепи, содержащей только актив­ное сопротивление r.

Вследствие сдвига фаз ср. мощность Р. П. т., измеряемая ваттметром, меньше произведения действующих значений тока и напряжения: Р=IUcos.

В цепи, не содержащей ни индуктив­ности, ни ёмкости, ток совпадает по фазе с напряжением (рис. 3). Закон Ома для действующих значений этой цепи имеет такую же форму, как и для цепи пост. тока: I=U/r. Актив­ное сопротивление цепи r определя­ется по активной мощности Р, затра­чиваемой в цепи: r=Р/I².

При наличии в цепи индуктивности L П. т. индуцирует в ней эдс самоин­дукции e_L=-Ldi/dt=-LI_mX

Xcos(t+)=LI_msin(t+-/2). Эдс самоиндукции противодействует изменению тока, и в цепи, содержащей только индуктивность, ток отстаёт по фазе от напряжения на четверть пе­риода, т. е. =/2 (рис. 4). Дейст­вующее значение e_L равно: ξ_L=IL=Ix_L, где x_L=L — индуктивное сопротивление цепи. Закон Ома для такой цепи имеет вид: I=u/x_l=U/L.



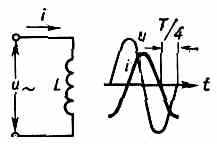
Рис. 4. Схема цепи и графики напряжения u и тока i в цепи, содержащей только ин­дуктивность L.


При напряжении и на конденсаторе ёмкости С заряд на его обкладках будет равен q=Cu. Периодические изменения и вызывают периодическое изменение q, и возникает ёмкостный ток:

i=dq/dt=C•du/dt=CU_mXcos(t+)=CU_msin(t++/2). Т. о., синусоидальный П. т., прохо­дящий через ёмкость, опережает по фазе напряжение на её зажимах на четверть периода, т. е. =-/2 (рис. 5). Эфф. значения в такой цепи связаны соотношением I=CU=U/x_c, где x_с=1/С — ё м к о с т н о е сопротивление цепи.

Если цепь П. т. состоит из последо­вательно соединённых r, L и С, то её п о л н о е сопротивление равно: z=(r²+x²), где х=x_l-x_c=L — -1/С — реактивное сопро­тивление цепи П. т. Соответственно



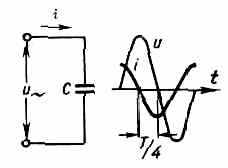
Рис. 5. Схема цепи и графики напряжения u и тока i в цепи, содержащей только ём­кость С.


закон Ома имеет вид: I=U/z= U/(r²+(L-1/C)²), а сдвиг фаз между током и напряжением опреде­ляется отношением реактивного сопро­тивления к активному: tg=x/r. В такой цепи при совпадении частоты вынужденных колебаний, создаваемых источником П. т., с резонансной часто­той ₀=l/LC индуктивное и ёмкост­ное сопротивления равны (L=l/C) и полностью компенсируют друг дру­га, сила тока максимальна и наблю­дается явление резонанса (см. Коле­бательный контур). В условиях ре­зонанса напряжения на индуктивно­сти и ёмкости могут значительно (ча­сто во много раз) превышать напря­жение на зажимах цепи.

Для расчётов разветвлённой цепи П. т. используют Кирхгофа правила. Несинусоидальность П. т. в электроэнергетич. системах обычно нежела­тельна, и принимаются спец. меры для её подавления. Но в цепях электро­связи, в полупроводниковых и элект­ронных устройствах несинусоидаль­ность создаётся самим рабочим про­цессом. Если среднее за период зна­чение тока не равно нулю, то он содержит постоянную составляющую. Для анализа процессов в цепях неси­нусоидального тока его представляют в виде суммы простых гармонич. со­ставляющих, частоты к-рых равны целым кратным числам осн. часто­ты: i=I₀+I_lmsin(t+₁)+I_2mXsin(2t +₂)+...+I_kmsin(kt+_k). Здесь I₀ — постоянная составляющая тока, I_1msin(t+₁) — первая гар­монич. составляющая (осн. гармо­ника), остальные члены — высшие гармоники. Расчёт линейных цепей несинусоидального тока на основе принципа суперпозиции ведётся для каждой составляющей (т. к. х_L и x_c зависят от частоты). Алгебр. сло­жение результатов таких расчётов да­ёт мгновенное значение силы (или на­пряжения) несинусоидального тока.

• Нелинейные электрические цепи. Элект­ромагнитное поле, 4 изд., М., 1979 (Теорети­ческие основы электротехники, под ред. Г. И. Атабекова, ч. 2—3); Касаткин А. С., Электротехника, 3 изд., М., 1973; Поливанов К. М., Линейные электри­ческие цепи с сосредоточенными постоян­ными, М., 1972 (Теоретические основы элект­ротехники, т. 1).

А. С. Касаткин.

ПЕРЕМЕЩЕНИЕ в механике, вектор, соединяющий положения движущейся точки в начале и в конце нек-рого промежутка времени; направлен век­тор П. вдоль хорды траектории точки. ПЕРЕНОРМИРОВКА (ренормировка) в квантовой теории поля, процедура изменения параметров, входящих в ур-ния движения квант. теории поля (КТП). В кач-ве таких параметров обычно выступают массы ч-ц, кон­станты связи, нормировка векторов состояния. Процедура П. преследует двоякую цель: а) введение в ур-ния параметров, имеющих непосредств. физ. смысл; б) устранение из теории бессмысленных расходящихся выраже­ний, возникающих в процессе реше­ния ур-ний по теории возмущений (см. Квантовая теория поля). Метод П. в КТП разработан амер. физиками Р. Фейнманом, Ю. Швингером, Ф. Дайсоном в 1944—49 и завершён Н. Н. Бо­голюбовым в 1955 — 57.

Процедура П. должна удовлетворять условию р е н о р м а л и з а ц и о н н о й и н в а р и а н т н о с т и, сос­тоящему в том, что наблюдаемые ве­личины, вычисленные как с помощью первоначальных, так и с помощью но­вых параметров, должны совпадать.

Поясним это на примере П. электрич. заряда в квант. электродинамике. Величина заряда эл-на определяется через силу, действующую на ч-цу в реальном эл.-магн. поле. Результатом её действия может быть отклонение

526


движущегося эл-на полем к.-л. заряж. источника. Если после вз-ствия

полем источника эл-н изменил свой четырёхмерный импульс (4-импульс)

l на l', это означает, что, обменявшись с источником виртуальным фотоном, эл-н передал последнему импульс q=l-l'. В КТП такой процесс описывается суммой Фейнмана диаграмм, изображённых на рис. 1 составляющих т. н. вершинную функцию Е(m*), зависящую от массы виртуального фотона m*=│q²│/с и грающую роль эффективного заряда.



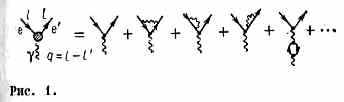
Эта сумма имеет вид ряда по «затравочному» заряду е₀ — параметру в исходных ур-ниях теории поля, харакризующему интенсивность вз-ствия,

Е(m*, е₀) =e0+(e³₀/ћc)f₁(m*)+... (1)

(где f₁ — нек-рая ф-ция от m*), причём первое слагаемое описывает диаграмму а, а второе — сумму остальных диаграмм, изображённых на рис. Величиной же физ. заряда, согласно обычному определению, наз. величина той ф-ции при m*=0 (реальное эл.-магн. поле), т.е.

е=Е(m*=0, е₀)=e₀+(e³₀/ћc)f(0}+ . . . Процедура П. заключается в том, что разложение (1) можно переписать в виде



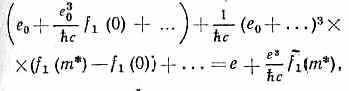
т. е. величину физ. заряда е приписать первой диаграмме, а вклады осталь­ных диаграмм переопределить так, чтобы при m*=0 они были бы равны пулю, напр. f^~₁(m*)=f₁(m*)-f₁(0); при том, хотя каждое из слагаемых бесконечно велико, их разность f^~₁ оказывается конечной.

Однако принятый способ определения заряда не единственный. Заряд можно было бы определять и через отклонение эл-на с к.-н. ненулевым квадратом передачи 4-импульса │q²│=²с², где  — нек-рое фиксиров. значение m*0. Такой новый заряд е_ по величине будет отличаться от об­щепринятого. Эфф. заряд Е(m*, , е_) будет иметь вид разложения (1), но уже по новому заряду е_, а вклады диаграмм с тремя и большим числом вершин, согласно процедуре П., долж­ны вычитаться в точке m*=, т. е. Е(m* =, , е_)=e_. Ренормализац. инвариантность для эфф. заряда означает, что для любой новой точки нормировки m*='

Е(m*, ', е_')=Е(m*, , е_), или, поскольку е_'=Е(', , е_), Е(m*, ', Е(', , е_))=Е(m*, , е_).

Это функц. уравнение эквивалентно дифф. ур-нию

m*(dE/dm*)=(E). (2) где  — нек-рая ф-ция Е. Ур-ние (2) явл. основным ур-нием ренормализац. группы. Оно говорит о том, что изме­нение эфф. заряда Е (т*) с изменением передачи 4-импульса полностью определя­ется ф-цией (E). Информация об этой ф-ции основывается почти исключительно на теории возмущений.



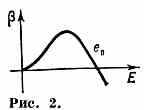
В частности, если (Е)>0 (как, напр., в квант. электродинамике), то эфф. заряд растёт с ростом т* и разло­жение (Е) в ряд по Е при достаточно большом Е становится несправедли­вым. Напротив, если (Е)<0 (как, напр., в квантовой хромодинамике), то с ростом m* эфф. заряд уменьшается и разложение (Е) становится всё более точным. Это случай т. н. асимптоти­ческой свободы. Интересен случай, когда (E) при нек-ром значении Е=е₀ меняет свой знак (рис. 2). Здесь хотя с ростом т* заряд и растёт, ско­рость этого роста (т. е. (Е)) умень­шается и при Е=е₀ обращается в нуль. Эфф. заряд с уменьшением расстояния (с ростом m*) стремится к конечной величине е₀. В этом пределе появляется новое св-во симметрии — масштабная инвариантность: ур-ния теории не изменяются, если все рас­стояния и времена изменить в одно и то же число раз.

• Проблемы физики микромира. Сб. ст., М., 1975 (Новое в жизни, науке, технике. Сер. Физика, № 9); Ф е й н м а н Р. Ф., Квантовая электродинамика, пер. с англ., М., 1964.

А. В. Ефремов.