П падение тела
| Вид материала | Документы |
- Тема «кинематика материальной точки», 29.33kb.
- Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
- Программа вступительных испытаний по физике механика, 48.4kb.
- Тема: строение тела животных, 47.92kb.
- Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
- Тема. Малые тела Солнечной системы, 383.39kb.
- Книга о душе, 521.77kb.
- Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
- Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
- Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.
ПАРАЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС, резонансное поглощение радиоволн в тв. в-ве, связанное с ориентацией дипольных электрич. моментов составляющих его частиц во внешнем электрич. поле. П. р. наблюдается в тех случаях, когда существует неск. эквивалентных равновесных направ-
521
лений ориентации диполей, разделённых невысокими потенц. барьерами, допускающими туннелирование (см. Туннельный эффект) из одного равновесного положения в другое с частотой, лежащей в диапазоне СВЧ. Электрич. поле смещает и расщепляет уровни энергии такой частицы, изменяя частоту переходов между ними. П. р. наблюдается при темп-ре T<10К в КСl с примесью ионов ОН-, CN- или Li+. В последнем случае дипольный момент возникает за счёт смещения примеси Li относительно центра занимаемого им места в решётке. П. р. используется для изучения внутрикристаллич. полей, определения типа примесных центров и др.
• Дейген М. Ф., Глинчук М. Д., Параэлектрический резонанс нецентральных ионов, «УФН», 1974, т. 114, в. 2, с. 185 — 211.
А. В. Францессон.
ПАРООБРАЗОВАНИЕ, переход в-ва из конденсиров. фазы (жидкой или твёрдой) в газовую (фазовый переход I рода), для осуществления к-рого в-ву необходимо подвести определённое кол-во теплоты. Различают след. виды П.: испарение (П. со свободной поверхности конденсиров. фазы, в случае тв. тела — сублимация) и кипение (П., характеризующееся возникновением пузырьков с насыщенным паром и ростом пузырьков в объёме жидкости).
ПАРСЕК (пк, рс), единица длины, применяемая в астрономии; 1 пк=206 265 а. е.=3,0857•1016 м. Звезда, расположенная на расстоянии 1 пк, имеет годичный параллакс, равный 1".
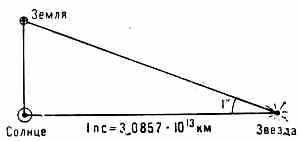
Копределению парсека.
ПАРТОНЫ (от лат. pars, род. падеж partis — часть), составляющие адронов, проявляющиеся в процессах с большой передачей четырёхмерного импульса, в частности в глубоко неупругих процессах.
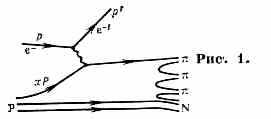
В модели П. считается, что адрон участвует в реакциях лишь нек-рой своей частью (партоном), несущей долю x четырёхмерного импульса (4-им-пульса) адрона Р, т. е. Рпартона= xРадрона. В первом приближении П. рассматриваются как точечные ч-цы, испытывающие только упругие соударения. Напр., глубоко неупругое рассеяние эл-на на протоне выглядит след. образом. Эл-н с 4-импульсом р упруго рассеивается на П. с 4-импульсом хР и приобретает 4-импульс р' (рис. 1). Далее рассеянный П. и «пассивный» остаток протона снова превращаются в адроны, образующие
две адронные струи. Согласно закону сохранения 4-импульса, импульс рассеянного П. равен q+хР, где q = р-р' — передача 4-импульса от эл-на к протону. Т. к. масса П. равна хМ, где М — масса протона, то (q+xP)2=x2M2c4. Отсюда следует, что
эл-н взаимодействует только с теми П., к-рые несут долю импульса х =-q2/2(Pq). Если число таких П. сорта а обозначить через Fa(x), то сечение глубоко неупругого рассеяния будет равно:
d/dq2dx=aFa(x)(d/dq2)a+ea'+e' (1) где d/dq2 (благодаря точечности П.) определяется ф-лой Мотта d/dq2~е2aћ/сq4 (еa — электрич. заряд П. сорта а). Т. о., формфактор глубоко неупругого рассеяния, определяемый как множитель при ф-ле Мотта, оказывается независящим от q2. Это св-во сечения глубоко неупругого рассеяния было названо скейлингом Бьёркена (см. Масштабная инвариантность).
Широкое распространение получила гипотеза, отождествляющая П. с кварками и глюонами. Существует неск. косвенных эксперим. указаний в пользу этой гипотезы, однако прямые доказательства (измерения ср. электрич. и ср. барионного зарядов адронных струй) пока отсутствуют. Комбинируя сечения глубоко неупругого рассеяния в пучках нейтрино и антинейтрино, к-рые взаимодействуют с разными кварками (v+р-+X, v~+р ++ X), можно получить распределения по импульсам всех кварков и антикварков по отдельности (рис. 2). Оказалось, что суммарный импульс всех кварков и антикварков в протоне составляет ок. 50% импульса протона, т. е. половина его импульса связана с нейтральными составляющими, названными глюонами.

Рис. 2. Распределение кварков N(x) и антикварков N~(x) в протоне.
Аналогично в модели П. рассматриваются и др. процессы с большой передачей 4-импульса: рождение в адрон-адронных соударениях пары +- с большой относит. энергией, рождение адронов с большим поперечным импульсом и т. д. Сечение каждого из них определяется [подобно (1)] распределением П. в адроне, к-рое не зависит от типа процесса, и сечением партонного подпроцесса, к-рое вычисляется. Это позволяет установить связь между разл. процессами.
Партонная модель получила в 70-х гг. обоснование в рамках квант. теории поля. Она оказалась связанной с достаточно быстрым убыванием эффективного заряда при уменьшении расстояния (r): Gэфф(r)<С/ln(r0/r), где С и r0 — нек-рые константы. Такое поведение характерно для теорий с размерной константой связи [g]=см-1 (в ед. ћ=1, с=1). Для теорий с логарифмич. убыванием эфф. заряда (асимптотическая свобода в квантовой хромодинамике) в ф-циях распределения остаётся слабая зависимость от q2, нарушающая скейлинг Бьёркена. При этом оказывается, что число «медленных» П. (z<<1) с ростом q2 должно возрастать, а число «быстрых» (х~1) — убывать. Подобная тенденция в поведении ф-ций распределения наблюдается экспериментально.
• Д р е л л С., Партоны и глубоко неупругие процессы при высоких энергиях, пер. с англ., «УФН», 1972, т. 106, в. 2.
А. В. Ефремов.
ПАРЦИАЛЬНАЯ ВОЛНА, волна с определённым орбит. моментом. См. Рассеяние микрочастиц.
ПАРЦИАЛЬНОЕ ДАВЛЕНИЕ (от позднелат. partialis — частичный), давление, к-рое имел бы газ, входящий в состав газовой смеси, если бы он один занимал объём, равный объёму смеси при той же темп-ре. Общее давление смеси газов равно сумме П. д. отд. составляющих смеси (см. Дальтона законы). Пространств. неоднородность П. д. определяет течение процессов диффузии данного газа, абсорбции, растворения и распределения его между двумя частями системы, разделёнными проницаемой для данного газа перегородкой (см. Осмос).
ПАРЦИАЛЬНОЕ СЕЧЕНИЕ, эффективное сечение рассеяния ч-ц с определённым орбит. моментом. См. Рассеяние микрочастиц.
ПАСКАЛЬ (Па, Ра), единица СИ давления и механич. напряжения. Назв. в честь франц. учёного Б. Паскаля (В. Pascal). 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределённой по поверхности площадью 1 м2.1 Па=1 Н/м2=10 дин/см2=0,102 кгс/м2 =10-5 бар=9,87Х10-6 атм=7,50•10-3 мм рт. ст.=0.102 мм вод. ст.
ПАСКАЛЬ-СЕКУНДА (Па•с, Pa•s), единица СИ динамич. вязкости; 1 Па•с равен динамич. вязкости среды, в к-рой при ламинарном течении и при разности скоростей слоев, находящихся на расстоянии 1 м по нормали к направлению скорости, равной 1 м/с, касательное напряжение равно 1 Па. 1 Па•с=10 пуаз=0,102 кгс•с/м2.
522
ПАСКАЛЯ ЗАКОН, закон гидростатики, согласно к-рому давление на поверхности жидкости, произведённое внеш. силами, передаётся жидкостью одинаково во всех направлениях. Установлен франц. учёным Б. Паскалем (опубл. в 1663). П. з. имеет большое значение для техники, напр. он используется в гидравлич. прессе.
ПАУЛИ ПРИНЦИП, фундаментальный закон природы, заключающийся в том, что две тождеств. ч-цы с полуцелым спином не могут одновременно находиться в одном состоянии. Сформулирован в 1925 швейц. физиком В. Паули (W. Pauli) для эл-нов в атоме и назван им принципом запрета, затем распространён на любые фермионы. В 1940 Паули показал, что принцип запрета — следствие существующей в релятив. квант. механике связи спина и статистики: ч-цы с полуцелым спином подчиняются Ферми — Дирака статистике, поэтому волн. ф-ция системы одинаковых фермионов должна быть антисимметричной относительно перестановки любых двух фермионов; отсюда и следует, что в одном состоянии может находиться не более одного фермиона.
П. п. сыграл решающую роль в понимании закономерностей заполнения электронных оболочек атома, послужил исходным пунктом для объяснения ат. и мол. спектров. Фундаментальна роль П. п. в квант. теории тв. тела и ат. ядра, а также в теории яд. реакций и реакций между элем. ч-цами.
• Теоретическая физика 20 века. [Памяти В. Паули. Переводы], М., 1962.
В. П. Павлов.
ПАУЛИ УРАВНЕНИЕ, уравнение нерелятивистской квант. механики, описывающее движение заряж. ч-цы со спином 1/2 (напр., эл-на) во внеш. эл.-магн. поле. Предложено швейц. физиком В. Паули в 1927.
П. у. явл. обобщением Шредингера уравнения, учитывающим наличие у ч-цы собств. механич. момента — спина. Ч-ца со спином 1/2 может находиться в двух разл. спиновых состояниях с проекциями спина +1:/2 и -1/2 на нек-рое направление, принимаемое обычно за ось s. В соответствии с этим волн. функция ч-цы (r, t) (где r — координата ч-цы, t — время) явл. двухкомпонентной, что принято записывать в виде матрицы-столбца:
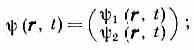
такая ф-ция наз. спинором. Проекции спина 1/2 отвечает случай =1,2=0, а -1/2 — случай =2, 1=0. Во внеш. магн. поле (с напряжённостью Н) компоненты волн. ф-ции «перемешиваются», что соответствует изменению направления спина.
В частном случае пост. однородного магн. поля (направление к-рого принимают за ось z) П. у. можно пред-
ставить в виде системы ур-нии для ф-ций 1, и 2:
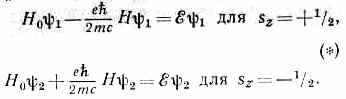
Здесь Н0 совпадает с гамильтонианом, входящим в ур-ние Шредингера для заряж. ч-цы во внеш. эл.-магн. поле, е и m — заряд и масса ч-цы, ξ — возможные (собственные) значения её энергии. Т. о., энергия эл-на зависит от ориентации спина но отношению к магн. полю. Этот факт можно интерпретировать как наличие у эл-на собственного (спинового) магн. момента =eћ/2mc. Вторые члены в (*) соответствуют потенц. энергии вз-ствия этого магн. момента с полем Н, равной для слабых полей (как и в классич. физике) — HН, где H — проекция на направление поля Н. Т. к. спин эл-на в размерных единицах равен 1/2ћ, то отношение спинового магн. момента к механич. (гиромагн. отношение, или магнитомеханическое отношение) равно e/тс, т. е. в два раза больше гиромагн. отношения для орбит. моментов. П. у. естеств. образом вытекает из релятив. Дирака уравнения, если считать, что скорость эл-на (v) мала по сравнению с с, и ограничиться первым приближением по v/c.
Я. В. Гольцов.
ПАШЕНА ЗАКОН устанавливает, что наименьшее напряжение зажигания газового разряда между двумя плоскими электродами есть величина постоянная (характерная для данного газа) при одинаковых значениях произведения pd, где р — давление газа, d — расстояние между электродами. Сформулирован нем. физиком Ф. Пашеном (F. Paschen) в 1889. П. з.— частный случай закона подобия газовых разрядов: явления в разряде протекают одинаково, если при увеличении или уменьшении давления газа во столько же раз уменьшить или, соответственно, увеличить размеры разрядного промежутка, сохраняя его форму геометрически подобной исходной. П. з. справедлив с тем большей точностью, чем меньше р и d. См. также Зажигания потенциал.
• См. лит. при ст. Электрические разряды в газах.
ПАШЕНА СЕРИЯ, см. Спектральные серии.
ПАШЕНА — БАКА ЭФФЕКТ, состоит в том, что в сильных магн. полях сложное зеемановское расщепление спектр. линий переходит в простое (см. Зеемана эффект). Сильными следует считать магн. поля, вызывающие расщепление уровней энергии, сравнимое с мультиплетным (см. Тонкая структура) и превосходящее его. В таких полях происходит упрощение картины расщепления — наблюдается расщепление линии на три компоненты (зеемановский триплет). Обнаружено Ф. Пашеном и нем. физиком Э. Баком (Е. Back) в 1912.
ПЕКЛЕ ЧИСЛО [по имени франц. учёного Ж. К. Пекле (J. С. Peclet)], безразмерное число, являющееся подобия критерием для процессов конвективного теплообмена. П. ч. Ре=vl/a=cpv/(/l), где l—характерный линейный размер поверхности теплообмена, v — скорость потока жидкости относительно поверхности теплообмена, а — коэфф. температуропроводности, cp — теплоёмкость при пост. давлении, — плотность и — коэфф. теплопроводности жидкости. Число Ре характеризует отношение между конвективным и мол. процессами переноса теплоты в потоке жидкости. При малых значениях Ре преобладает мол. теплопроводность, а при больших — конвективный перенос теплоты. П. ч. связано с Рейнольдса числом Re и Прандтля числом Рr соотношением Pe=Re•Pr.
ПЕЛЛЕТРОН, см. в ст. Электростатический генератор.
ПЕЛЬТЬЕ ЭФФЕКТ, выделение или поглощение теплоты при прохождении электрич. тока I через контакт двух разл. проводников. Выделение теплоты сменяется поглощением при изменении направления тока. Открыт франц. физиком Ж. Пельтье (J. Peltier) в 1834. Кол-во теплоты Qп=ПI, где П — коэффициент Пельтье, равный: П=T. Здесь Т — абс. темп-pa, —разность термоэлектрич. коэфф. проводников.
П. э. объясняется тем, что ср. энергия носителей тока зависит от их энергетич. спектра, концентрации и механизмов их рассеяния и поэтому в разных проводниках различна. При переходе из одного проводника в другой эл-ны либо передают избыточную энергию атомам, либо пополняют недостаток энергии за их счёт. В первом случае вблизи контакта выделяется, а во втором поглощается теплота Пельтье. При переходе эл-нов из полупроводника в металл энергия эл-нов проводимости ПП значительно выше уровня Ферми металла, и эл-ны отдают свою избыточную энергию. При противоположном направлении тока из металла в ПП могут перейти только те эл-ны, энергия к-рых выше дна зоны проводимости ПП. Тепловое равновесие в металле при этом нарушается и восстанавливается за счёт тепловых колебаний крист. решётки. При этом поглощается теплота Пельтье. На контакте двух ПП или двух металлов также выделяется (или поглощается) теплота Пельтье вследствие того, что ср. энергия носителей заряда по обе стороны контакта различна.
П. э. используется для охлаждения в холодильных установках и в нек-рых электронных приборах.
• См. лит. при ст. Термоэлектрические явления.
Л. С. Стальбане.
ПЕННИНГА РАЗРЯД, тлеющий разряд в продольном магн. поле. Впервые
523
исследован голл. физиком Ф. Пеннингом (F. Penning) в 1937. Из-за большой длины пути эл-нов, движущихся по спиральным траекториям вокруг силовых линий магн. поля, значительно возрастает вероятность ионизации, что обеспечивает существование разряда при низких давлениях р, вплоть до 10-5—10-6 мм рт. ст. Значение рмин сильно зависит от конструкции разрядного устройства. Часто применяются коаксиальные системы, в к-рых П. р. может существовать вплоть до 10-13мм рт. ст. П. р. используется в нек-рых типах вакуумметров, а также в эл.-магн. сорбционных вакуумных насосах.
Л. А. Сена.
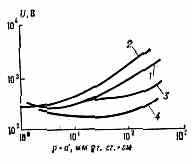
ПЕННИНГА ЭФФЕКТ, снижение зажигания потенциала разряда в газе, обусловленное присутствием примеси другого газа, потенциал ионизации к-рого ниже энергии возбуждения метастабильного уровня осн. газа. Объяснение этого эффекта дано Ф. Пеннингом в 1928. В отсутствии примеси эл-ны, ускоренные в электрич. поле, отдают свою энергию атомам, переводя их в метастабильное состояние. Вследствие этого вероятность ионизации электронным ударом мала и напряжение зажигания оказывается высоким. При наличии примеси происходят столкновения возбуждённых метастабильных атомов осн. газа с атомами примеси, в результате чего последние ионизуются за счёт энергии, освобождающейся при переходе метастабильных атомов в основное состояние (см. Удары второго рода). Появление такой дополнит. ионизации приводит к снижению эфф. потенциала ионизации среды и, следовательно, к снижению напряжения зажигания разряда U. На рис.. представлена зависимость U (в логарифмич. масштабе) от произведения давления газа р на расстояние d между электродами в чистом неоне (1), чистом аргоне (2), неоне с примесью 5•10-4% аргона (3) и неоне с примесью 0,1% аргона (4).
Л. А. Сена.
ПЕНТАПРИЗМА, см. Отражательные призмы.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ, один из двух осн. законов термодинамики, представляет собой закон сохранения энергии для систем, в к-рых существ. значение имеют тепловые процессы. П. н. т. было сформулировано в сер. 19 в. в результате работ нем. учёного Ю. Р. Майера, англ. физика Дж. П. Джоуля и нем. физика Г. Гельмгольца (см. Энергии сохранения закон). Согласно П. н. т., термодинамич. система может совершать работу только за счёт своей
внутр. энергии или к.-л. внеш. источников энергии. П. н. т. часто формулируют как невозможность существования вечного двигателя 1-го рода, к-рый совершал бы работу, не черпая энергию из к.-л. источника.
При сообщении термодинамич. системе нек-рого кол-ва теплоты Q в общем случае изменяется её внутренняя энергия на U и система совершает работу А:
Q =U+A. (1) Ур-ние (1), выражающее П. н. т., явл. определением изменения внутр. энергии системы (U), т. к. Q и А — независимо измеряемые величины. Внутр. энергию системы U можно, в частности, найти, измеряя работу системы в адиабатич. процессе (т. е. при Q=0): Aад =-U, что определяет U с точностью до нек-рой аддитивной постоянной U0:
U=U+U0. (2) П. н. т. утверждает, что U явл. функцией состояния системы, т. е. каждое состояние термодинамич. системы характеризуется определ. значением U, независимо от того, каким путём система приведена в данное состояние (в то время как, значения Q и А зависят от процесса, приведшего к изменению состояния системы). При исследовании термодинамич. свойств физ. системы П. н. т. обычно применяется совместно со вторым началом термодинамики.
• Леонтович М. А., Введение в термодинамику, 2 изд., М.—Л., 1952; П у т и л о в К. А., Термодинамика, М., 1971; Г е л ь ф е р Я. М., История и методология термодинамики и статистической физики, 2 изд., М., 1981.
ПЕРЕБРОСА ПРОЦЕССЫ, процессы столкновения квазичастиц в кристалле, при к-рых их суммарный квазиимпульс изменяется на величину 2ћb, где b — вектор обратной решётки. П. п.— результат периодичности расположения атомов в кристалле.
ПЕРЕГРЕВ, 1) нагрев жидкости выше её точки кипения (при данном давлении) или нагрев твёрдого крист. в-ва выше темп-ры его фазового перехода из одной модификации в другую (напр., ромбич. серы в моноклинную). Перегретое в-во находится в неустойчивом, метастабильном состоянии. Практически при всяком фазовом переходе, связанном с поглощением или отдачей теплоты, небольшой П. или переохлаждение необходимы для того, чтобы процесс шёл с конечной скоростью. 2) Нагрев пара выше темп-ры насыщения при том же давлении. Водяной перегретый пар широко применяется в теплотехнике.
ПЕРЕГРЕТЫЙ ПАР, пар, имеющий темп-ру выше темп-ры насыщения при том же давлении (см. Насыщенный пар). П. п. служит рабочим телом в тепловых двигателях, турбинах и т. д.
