П падение тела
| Вид материала | Документы |
- Тема «кинематика материальной точки», 29.33kb.
- Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
- Программа вступительных испытаний по физике механика, 48.4kb.
- Тема: строение тела животных, 47.92kb.
- Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
- Тема. Малые тела Солнечной системы, 383.39kb.
- Книга о душе, 521.77kb.
- Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
- Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
- Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.
(r — радиус-вектор точки), то возможно усиление или генерация двух волн с частотами 1, 2 и волн. векторами k1, k2 при выполнении условий волн. синхронизма н=1±2, kн=k1±k2.
• Люиселл У., Связанные и параметрические колебания в электронике, пер. с англ., М., 1963; Э т к и н В. С., Г е р ш е н з о н Е. М., Параметрические системы СВЧ на полупроводниковых диодах, М., 1964; Регенеративные полупроводниковые параметрические усилители (Некоторые вопросы теории и расчета), М., 1965; К а п л а н А. Е., Кравцов Ю. А., Р ы л о в В. А., Параметрические генераторы и делители частоты, М., 1966; Квантовая электроника, М., 1969, с. 339 (Маленькая энциклопедия).
Л. А. Островский, Н. С. Степанов.
ПАРАМЕТРИЧЕСКИЙ ГЕНЕРАТОР СВЕТА, источник когерентного оптич. излучения, в к-ром энергия мощной световой волны фиксированной частоты преобразуется в излучение более низкой частоты. Процесс преобразования осуществляется в нелинейной среде (в среде с нелинейной поляризацией) и имеет много общего с параметрич. возбуждением колебаний радиодиапазона. Параметрич. возбуждение в радиодиапазоне происходит в колебат. контуре при модуляции его параметров, обычно ёмкости. Периодич. изменение ёмкости с частотой накачки н приводит к возбуждению в контуре колебаний с частотой н/2 (см. Параметрическая генерация и усиление электромагнитных колебании). Аналогично могут возбуждаться и световые колебания. Однако в этом случае параметрич. явления носят волн. характер и происходят не в контуре с нелинейным конденсатором, а в нелинейной среде. Последнюю можно представить в виде цепочки колебат. контуров с ёмкостью, модулированной бегущей световой волной. Световая волна большой интенсивности частоты н (волна накачки), распространяясь в среде с квадратичной нелинейностью, модулирует её диэлектрическую проницаемость (см. Нелинейная оптика). Если электрич. поле волны накачки
Eн=Eноsin(нt-kr+но),
где k — волновой вектор, но — нач. фаза; r — пространств. координата точки, то среды также изменяется по закону бегущей волны:
=0[1+msin(нt-kнr+но)].
Здесь m=4Ено/0 — глубина модуляции диэлектрич. проницаемости, X — нелинейная диэлектрич. восприимчивость, характеризующая нелинейные св-ва среды, 0 — диэлектрич. проницаемость среды без накачки. В каждой точке среды, куда приходит волна накачки, возбуждаются световые колебания с частотами 1 и 2, связанные с н соотношением: н=1+2 (аналогично параметрич. возбуждению колебаний радиочастоты в двухконтурной системе). Волна накачки отдаёт им свою энергию наиболее эффективно, если во всей области вз-ствия волн между фазами волн сохраняется соотношение:
н(r)=1(r)+2(r). (1)
Т. к. в бегущих волнах фазы изменяются в пр-ве по закону (r)=-kr+0, то из (1) следует т. н. условие фазового (или волнового) синхронизма:
kн=k1+k2. (2) Соотношение (2) означает, что волн. векторы волны накачки kн и возбуждаемых волн k1 и k2 образуют треугольник, причём kнk1+k2. Равенство соответствует распространению волн в одном направлении.
При фазовом синхронизме амплитуды возбуждаемых волн по мере их распространения в глубь среды непрерывно увеличиваются:
E=E0exp[((m/2)(k1k2)-)x], (3)
где б — коэфф. затухания волны в обычной (линейной) среде, х — расстояние, проходимое световой волной в среде. Параметрич. возбуждение света происходит, если поле накачки превышает порог: Ено>(/x)(k1k2). Условие синхронизма (2) выполняется, если показатели преломления nн, n1 и n2 среды для частот н, 1 и 2 удовлетворяют неравенству:
[nн-n1]1+[nн-n2]20. (4) В среде с норм. дисперсией, когда n увеличивается с ростом частоты , параметрич. генерация света неосуществима, Т. К. nн>n1 и nн>n2.
Для выполнения условия синхронизма необходимо, чтобы среда обладала аномальной дисперсией — полной: nн<n1, nн
Такой средой могут служить анизотропные кристаллы, в к-рых могут распространяться два типа волн — обыкновенная о и необыкновенная в (см. Кристаллооптика, Двойное лучепреломление). Условие фазового
синхронизма может быть осуществлено, если использовать зависимость показателя преломления необыкновенной волны nе в кристалле не только от частоты, но и от направления распространения. Напр., в одноосном отрицат. кристалле показатель преломления обыкновенной волны n° боль-
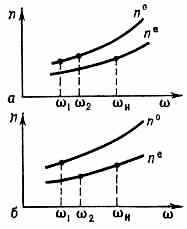
Рис. 1. Зависимость показателя преломления для обыкновенной n° и необыкновенной n волн в одноосном кристалле от частоты со в случае полной (о) и частичной (б) аномальной дисперсии.
ше пе (волны накачки), зависящего от направления и распространения относительно оптич. оси кристалла. Если волн. векторы параллельны друг другу, то условию фазового синхронизма соответствует определ. направление в кристалле, вдоль к-рого:
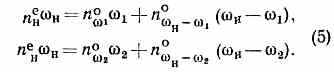
Угол с между этим направлением и оптич. осью кристалла наз. углом синхронизма. Он зависит от частот накачки н и одной из возбуждаемых волн 1 или 2. Изменяя угол между направлением распространения волны накачки и оптич. осью кристалла, т. е. пово-
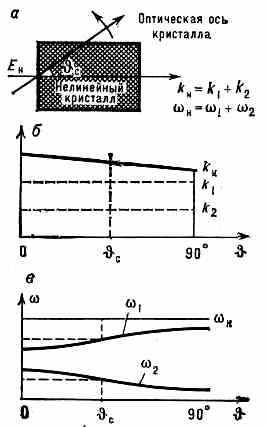
Рис. 2. а — условие синхронизма в нелинейном кристалле, с — угол синхронизма; б — изменение длин волн. векторов необыкновенной волны накачки kн и обыкновенных волн k1 и k2 при повороте кристалла; в — зависимость частот (1 и 2, для к-рых выполняется условие синхронизма, от .
519
рачивая кристалл, можно перестраивать частоту П. г. с. (рис. 2). Существуют и др. способы перестройки частоты П. г. с., связанные с зависимостью n от темп-ры, внеш. электрич. поля и т. д.
Нарастание амплитуд синхронно возбуждаемых волн с расстоянием по экспоненциальному закону (3) происходит в П. г. с. бегущей волны. Однако в таких П. г. с. достаточно большую мощность излучения на перестраиваемых частотах можно получить в очень протяжённых кристаллах диаметром порядка десятков или сотен см. Для увеличения мощности П. г. с. нелинейный кристалл помещают внутри оптического резонатора, благодаря чему волны пробегают кристалл многократно, т. е. за время действия импульса накачки увеличивается эфф. длина кристалла (рис. 3). В процессе возбуждения световых колебаний в резонаторном П. г. с. их амплитуды нарастают во времени до тех пор, пока от волны накачки не будет забираться значит. доля энергии. Перестройка частоты резонаторного П. г. с. происходит небольшими скачками, определяемыми разностью частот, соответствующих продольным модам резонатора.
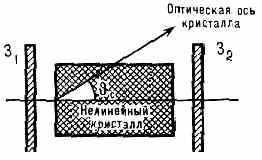
Рис. 3. Схема резонаторного параметрич. генератора света: З1 и З2 — зеркала, образующие резонатор для обеих генерируемых волн или для одной из них.
Плавную перестройку частоты можно осуществить, комбинируя повороты кристалла, его нагрев, воздействие внеш. электрич. поля с изменением параметров резонатора. Существуют однорезонаторные схемы П. г. с., в к-рых резонатор имеется только для одной из возбуждаемых световых волн, и двухрезонаторные схемы П. г. с., где есть резонаторы для обеих возбуждаемых волн.
П. г. с. предложен в 1962 С. А. Ахмановым и Р. В. Хохловым. В 1965 созданы первые П. г. с. Джорджмейном и Миллером (США) и несколько позднее Ахматовым и Хохловым с сотрудниками. Источником накачки в П. г. с. служит лазер. Особое значение П. г. с. имеют для ИК области спектра. П. г. с. работают в диапазонах длин волн 1,45—4,2 мкм, 8—10 мкм и 16 мкм. П. г. с. обеспечивают перестройку частоты в пределах 10—20%. Уникальные хар-ки П. г. с.: когерентность излучения, узость спектр. линий, высокая мощность, плавная
перестройка частоты — делают его одним из осн. приборов нелинейной спектроскопии (активная спектроскопия и др.), а также позволяют использовать его для селективного воздействия на в-во, в частности на биол. объекты.
• Ахманов С. А., Хохлов Р. В., Параметрические усилители и генераторы света, «УФН», 1966, т. 88, в. 3, с. 439; Я р и в А., Квантовая электроника, пер. с англ., 2 изд., М., 1980; Квантовая электроника, М., 1969 (Маленькая энциклопедия); Ц е р н и к е Ф., М и д в и н т е р Дж., Прикладная нелинейная оптика, пер. с англ., М., 1976.
А. П. Сухорукое.
ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС, явление раскачки колебаний при периодич. изменении параметров тех элементов колебат. системы, в к-рых сосредоточивается энергия колебаний (реактивные или энергоёмкие параметры). П. р. возможен в колебат. системах различной физ. природы. Напр., в колебательном контуре реактивными параметрами явл. ёмкость С и индуктивность L, в к-рых запасены
электрич. энергия Wэ=q2/2C и магн.
энергия Wм=LI2/2 (q — заряд на обкладках конденсатора, I — ток в катушке индуктивности). Собств. колебания в контуре без потерь с постоянными С и L происходят с частотой 0=1/LC. При этом полная энергия W=Wэ+Wм, запасённая в контуре, остаётся неизменной, происходит лишь её периодич. трансформация из электрич. в магнитную и обратно с частотой 20. Изменение параметров С и L, сопровождающееся затратой работы внеш. сил (накачка), приводит к изменению полной энергии системы. Если ёмкость С изменить скачком (за время, малое по сравнению с периодом собств. колебаний Т0=2/0) (рис. 1, а), то заряд q скачком
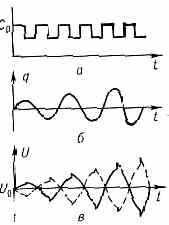
Рис. 1. Связь между изменениями ёмкости С конденсатора (а), заряда q на его обкладках (б) и напряжения U (в) при параметрич. резонансе в колебат. контуре.
измениться не может (иначе ток I=aq/dt, рис. 1, б). В результате напряжение на ёмкости U=q/C и электрич. энергия Wэ=q2/2C изменяются обратно пропорц. С, причём совершаемая при этом работа пропорц. q2. Если изменять ёмкость С периодически в такт с изменениями Wэ (обусловленными собств. колебаниями), уменьшая её в моменты, когда │q│ и Wэ максимальны, и увеличивая, когда эти величины равны нулю (рис. 1), то в среднем за период над системой совершается
работа и, следовательно, полная энергия и амплитуда колебаний будут монотонно нарастать.
Раскачка колебаний возможна при изменении С или L по любому периодич. закону с периодом Тн или частотой н, определяемыми соотношениями:
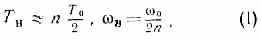
где n — целое число. Наиболее эфф. раскачка имеет место при n=1, когда частота накачки н равна частоте колебаний Wэ и Wм в системе 0. Нарастание колебаний возможно не только при точном выполнении соотношения (1), но и в нек-рых конечных интервалах значений н вблизи 0 (в зонах неустойчивости), ширина зон тем больше, чем сильнее изменяются параметры С и L. Изменение параметра, напр. ёмкости С, характеризуют величиной m=(Cмакс-Cмин)/(Cмакс+Cмин)
наз. глубиной изменения параметра (рис. 2).
П. р. приводит к нарастанию малых нач. возмущений, напр. неизбежных
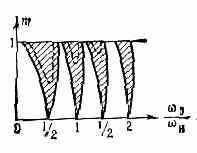
Рис. 2. Области значений m, в к-рых возможен параметрич. резонанс; 0 — частота собств. колебаний, н — частота накачки (изменения параметра).
во всякой системе флуктуации, среди к-рых всегда найдётся составляющая с подходящей фазой по отношению к фазе изменения параметров, т. е. к самовозбуждению колебаний. В отсутствии потерь энергии самовозбуждение наступает при сколь угодно малом изменении параметров. Если же в системе имеются потери (напр., в контуре присутствует сопротивление Л), то самовозбуждение происходит только при достаточно больших изменениях С или L, когда параметрич. накачка энергии превосходит потери. Зоны неустойчивости при этом соответственно уменьшаются или даже исчезают совсем (при больших потерях). Нарастание колебаний при П. р. не происходит беспредельно, а ограничивается при достаточно больших амплитудах разл. нелинейными эффектами. Напр.: зависимость сопротивления Л от тока в контуре может приводить к увеличению потерь по мере возрастания амплитуды колебаний, а зависимость ёмкости от напряжения на ней — к изменению периода собств. колебаний Т0 и в результате — к увеличению расстройки между значениями н и 0/2n. Равновесие наступает тогда, когда параметрич. накачка энергии в среднем за период компенсируется джоулевыми потерями (см. Параметрическая генерация и усиление электромагнитных колебаний).
520
Пример механич. системы, в к-рой возможен П. р.,— маятник в виде груза массы т, подвешенного на нити, длину l к-рой можно изменять (рис. 3). Маятник с неподвижной точкой подвеса совершает собств. колебания с частотой 0=g/l, причём сила натяжения нити (равная по величине сумме центробежной силы и составляющей силы тяжести, направленной
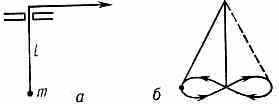
Рис. 3. а — устройство маятника с переменной длиной l подвеса; б — схема движения тела маятника за один период.
вдоль нити) максимальна в нижнем положении груза и минимальна в крайних. Поэтому если уменьшать l в нижнем и увеличивать в крайних положениях [при этом снова выполняется соотношение (1)], то работа внеш. силы, совершаемая в среднем за период, оказывается положительной и колебания могут раскачиваться. На П. р. основано самораскачивание на качелях, когда эфф. длина маятника периодически изменяется при приседаниях и вставаниях качающегося. П. р. учитывается в небесной механике при расчёте возмущений планетных орбит, вызванных влиянием др. планет.
В колебат. системах с неск. степенями свободы (напр., в системе из двух связанных контуров, маятников и др.) возможны нормальные колебания (моды) с разл. частотами 1, 2. Поэтому колебания энергии, запасённой в к.-л. реактивном элементе, содержат не только составляющие с частотами 21, 22, но и с частотами, равными суммам и разностям разл. нормальных частот. Соответственно нарастание колебаний здесь возможно как при выполнении условия (1) для любой из норм. частот, так и, напр., при изменении параметра с суммарной частотой:
н =1+2. (2)
П. р. приводит к самовозбуждению обоих норм. колебаний с определ. соотношением фаз. Резонансная связь мод возможна также при н=1-2, однако при этом вместо самовозбуждения происходит лишь периодич. перекачка энергии между модами. Соотношение (2) выражает закон сохранения энергии при распаде кванта «накачки» с энергией ћ на два кванта: ћ1 и ћ2. Отсюда следует также, что мощность Рн, поступающая в колебат. систему на частоте н, и мощности P1,P2 потребляемые на частотах 1 и 2, пропорц. соответствующим частотам (частный случай т. н. соотношений Мэнли — Роу):
Pн/н=P1/1=P2/2 (3)
В колебат. системах с распределёнными параметрами, обладающих бесконечным числом степеней свободы, также возможно возбуждение норм. колебаний в результате П. р. Классич. пример — опыт Мельде (1859), в к-ром наблюдалось возбуждение поперечных колебаний (стоячих волн) в струне, прикреплённой одним концом к ножке камертона,
колебания к-рого периодически меняют натяжение струны (рис. 4) с частотой, вдвое большей частоты собств. поперечных колебаний. П. р. может приводить к раскачке изгибных колебаний вращающихся валов. Др. пример — опыт Фарадея (1831), в к-ром вертикальные колебания сосуда с водой приводят к возбуждению стоячей поверхностной волны с удвоенным периодом.
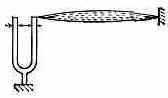
Рис. 4. Параметрич. возбуждение колебаний струны.
Существенная особенность П. р. в системах с распределёнными параметрами состоит в том, что его эффективность зависит от соотношения между законом изменения параметров системы в пр-ве и пространств. структурой колебаний (волн). Напр., если накачка, изменяющая параметры среды, представляет собой бегущую волну с частотой н и волновым вектором kн, то возбуждение пары норм. волн с частотами 1, 2 и волн. векторами k1, k2 осуществляется, если выполняются условия П. р. как во времени, так и в пр-ве:
н=1+1; kн=k1+k2. (4)
На квант. языке эти условия, обобщающие (2), означают, что при распаде кванта накачки сохраняются как энергия, так и импульс (ћk). Нарастание амплитуд волн во времени и пр-ве (распадная неустойчивость) также ограничивается нелинейными эффектами: если значит. часть энергии накачки израсходована на возбуждение этих волн, то возможен обратный процесс — рост энергии накачки за счёт ослабления волн на частотах 1, 2; в среде без потерь такой обмен энергией происходит периодически. Параметрические и нелинейные резонансные вз-ствия волн характерны, напр., для разл. типов волн в плазме, мощных световых волн (см. Параметрический генератор света), волн в электронных пучках и др. волн. процессов.
• Мандельштам Л. И., Лекции по теории колебаний, М., 1972; Х а я с и Т., Нелинейные колебания в физических системах, пер. с англ., М., 1968; Каудерер Г., Нелинейная механика, пер. с нем., М., 1961, ч. 2, гл. 3; С и л и н В. П., Параметрический резонанс в плазме, М., 1965.
Л. А. Островский, Н. С. Степанов.
ПАРАМЕТРЫ СОСТОЯНИЯ (термодинамические параметры), физ. величины, характеризующие состояние
термодинамич. системы: темп-pa, давление, уд. объём, намагниченность, электрич. поляризация и др. Различают э к с т е н с и в н ы е П. с., пропорц. массе системы, и и н т е н с и в н ы е П. с., не зависящие от массы системы. К экстенсивным П. с. относятся объём, внутренняя энергия, энтропия, энтальпия, Гиббса энергия, Гельмгольца энергия (свободная энергия), к интенсивным — давление, темп-pa, концентрация, магн. индукция и др. Не все П. с. независимы, так что равновесное состояние системы можно однозначно определить, установив значения огранич. числа П. с. (см. Уравнение состояния, Гиббса правило фаз).
ПАРАПРОЦЕСС (истинное намагничивание), возрастание абс. величины самопроизвольной намагниченности JS ферро- и ферримагнетиков под действием внеш. магн. поля Н. П. наступает после процессов «технич. намагничивания», связанных лишь с изменением направления векторов Js, и наблюдается в полях, превышающих значение поля технич. магн. насыщения Hs (см. Намагничивание). П. обусловлен ориентацией в поле Н элементарных носителей магнетизма (спиновых и орбитальных магнитных моментов атомов или ионов), оставшихся не повёрнутыми в направлении результирующей намагниченности вследствие «дезорганизующего» действия теплового движения. П.— завершающий этап намагничивания, на к-ром с увеличением И (если H>Hs) Js стремится приблизиться к величине абс. насыщения J0, т. е. к намагниченности, к-рую имел бы ферромагнетик при абс. нуле темп-ры (J0 соответствует полной упорядоченности магн. моментов носителей магнетизма). При П. магн. поле, поворачивая магн. моменты атомов, вызывает изменение обменной энергии магнетика. В магнетиках с одной магн. подрешёткой (ферромагнетиках) П. максимален вблизи точки Кюри, где велика концентрация магн. моментов, дезориентированных тепловым движением. В магнетиках с неск. магн. подрешётками (ферримагнетиках, в частности ферритах) П. может быть велик и вдали от точки Кюри за счёт «ослабленных» обменных внутриподрешёточных ц межподрешёточных вз-ствий.
9 Белов К. П., Ферриты в сильных магнитных полях, М., 1972.
К. П. Белое.
