П падение тела

Вид материала

Документы

Содержание Перенос излучения Перенос энергии Обмен­ное взаимодействие) Переноса явления Переносное движение ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕ­НИЯ (коммутационные соотношения) Пересыщенный пар Переходные металлы Период колебаний Период полураспада Периодическая система Атом). Число хим. элементов в периоде равно числу эл-нов в слое, к-рое строго определено в соответствии с Паули принципом В. Г. Дашевский.

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПЕРЕНОС ИЗЛУЧЕНИЯ, распрост­ранение эл.-магн. излучения (напр., оптического излучения) в среде при наличии процессов испускания, пог­лощения или рассеяния. Процесс П. и. представляет собой пространст­венно-частотное преобразование поля излучения, характеризующегося рас­пределением интенсивности излуче­ния по частотам, координатам и на­правлениям переноса лучистой энер­гии. Поле излучения полностью опре­деляется заданием спектр. интенсивностей излучения I_v=I_v(r, , t), таких, что величина I_vdvddSdt есть кол-во лучистой энергии в спектр. интервале (v, v+dv) и в телесном угле d, протекающей за время dt через площадку dS, помещённую в точке r перпендикулярно выбранному направ­лению.

Прохождение пучка света через в-во сопровождается его ослаблением вслед­ствие поглощения и рассеяния кван­тов света или усилением вследствие процессов вынужденного и спонтан­ного испускания и рассеяния. Изме­нение спектр. интенсивности излуче­ния подчиняется осн. ур-нию П. и., получаемому из условия баланса из­лучения в среде и представляющему

собой дифф. ур-ние в частных произ­водных относительно интенсивности, как функции координат, времени и направления. В общем случае ур-ние П. и. не решается, однако в конкрет­ных задачах допускаются упрощения и решение возможно. Так, для стацио­нарного поля излучения изменение интенсивности при прохождении па­раллельного пучка в среде с малой частотной дисперсией есть dI/dx=-I, где  характеризует суммар­ное ослабление света в среде с учётом процессов поглощения, вынужденного испускания и рассеяния. Решение этого ур-ния приводит к известному экспоненциальному закону ослабле­ния света с расстоянием х (Бугера — Ламберта — Бера закон).

С формальной точки зрения задачи П. и. можно разделить на два класса. К первому относятся процессы, в к-рых можно пренебречь частотной трансформацией поля излучения при его вз-ствии с в-вом. Так, напр., рас­сеяние света атмосферами планет рас­сматривается как П. и. без изменения частоты в процессах рассеяния. Ко второму классу относятся процессы, когда существенно перераспределение спектр. интенсивностей излучения I_v в результате вз-ствия излучений разл. частот с в-вом. Подобная ситуа­ция возникает, напр., при прохож­дении света в резонансной среде, где имеется уширение контура спектр. линии за счёт процессов столкновения.

Вообще говоря, ур-ние П. и. опи­сывает поле неравновесного излуче­ния. Однако в процессах П. и. в со­здании результирующей интенсивно­сти в заданной точке пр-ва участвуют лишь кванты, приходящие из непосредств. окрестности (неск. длин про­бега); остальные не доходят, погло­щаясь и рассеиваясь в пути. Т. о., даже если оптически плотная среда термодинамически неравновесна, это почти не сказывается на интенсивно­сти излучения в рассматриваемой точ­ке и становится возможным локальное равновесие излучения с в-вом. Суще­ствование локального равновесия важно для мн. задач П. и., к-рые ре­шаются в приближении лучистой те­плопроводности, сводящем осн. ур-ние П. и. к диффузионному, методы реше­ния к-рого хорошо разработаны.

Исторически процессы П. и. впер­вые исследовались в астрофизике. Изучение распределения темп-ры и поля излучения в фотосферах звёзд для расчёта их светимости — пример классич. задачи, на основе к-рой была построена теория П. и. и разрабо­таны методы решения ур-ния переноса. В атмосфере П. и. ответствен за ряд физ. явлений (напр., голубой цвет неба обусловлен процессами рассея­ния в атмосфере солн. света). П. и. следует учитывать в задачах газодина­мики, в ударных волнах большой ин-

527


тенсивности и т. п. Всё большее значение приобретает изучение процессов П. и. в исследовании плазмы, параметры к-рой невозможно интер­претировать без учёта явлений пере­носа, в понимании процессов в лазе­рах и квантовых усилителях, где неравновесное поле излучения опре­деляет практически все рабочие пара­метры. Специфика процессов П. и. в этом случае определяется тем, что излучение распространяется в сильно неравновесной резонансной среде, возбуждённой внеш. источником, когда благодаря инверсии населён­ности ат. энергетич. уровней вынуж­денное испускание преобладает над поглощением. При этом происходит не ослабление света по мере прохож­дения его через среду, а усиление с сохранением его когерентности.

• У н з о л ь д А., Физика звездных атмос­фер, пер. с нем., М., 1949; Чандрасекар С., Перенос лучистой энергии, пер. с англ., М., 1953; Соболев В. В., Пере­нос лучистой энергии в атмосферах звезд и планет, М., 1956; Зельдович Я. Б., Р а й з е р Ю. П., Физика ударных волн и высокотемпературных гидродинамических явлений, 2 изд., М., 1966.

В. Л. Комолое.

ПЕРЕНОС ЭНЕРГИИ, совокупность безызлучат. процессов в в-ве, при ко­торых энергия электронного возбуж­дения передаётся от возбуждённой ч-цы (молекулы, атома, иона) к невозбуж­дённой, находящейся от первой на расстоянии, меньшем длины волны возбуждающего излучения. П. э. обус­ловлен эл.-магн. вз-ствием между возбуждённой и невозбуждённой ч-цами — донором и акцептором энергии, соответственно, и осуществляется при выполнении условия резонанса для них, к-рое выражается в необходи­мости перекрывания спектров люми­несценции донора и поглощения ак­цептора. Процессы П. э. отличаются от процессов переноса излучения, при к-рых акцептор поглощает фотон, испущенный возбуждённой молекулой-донором, находящейся от акцептора на расстоянии, большем длины волны излучения. В частности, при П. э. благодаря вз-ствию ч-ц время жизни донора на возбуждённом уровне энер­гии уменьшается, а при переносе излучения, напротив, увеличивается.

По механизму вз-ствия ч-ц разли­чают мультипольный (индуктивно-резонансный) и обменный (см. Обмен­ное взаимодействие) П. э. Если элек­тронные переходы в молекулах донора и акцептора разрешены отбора пра­вилами, то осн. роль играет диполь-дипольный П. э., для к-рого характер­ны расстояния переноса ~2—8 нм. Обменный П. э. имеет место при пере­крывании электронных оболочек доно­ра и акцептора и происходит на рас­стоянии ~1—2 нм. При обменном П. э. суммарный спин системы донор — акцептор должен сохраняться.

Вероятность W (или скорость) ди­поль- дипольного П. э. (число актов

переноса в единицу времени) может быть выражена через оптические ха­рактеристики взаимодействующих мо­лекул:



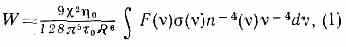
где v — частота (волн. число), F(v) — нормированный спектр люминесцен­ции донора, т.е. ∫F(v)dv=l, (v)—

эффективное сечение поглощения ак­цептора, ₀ и ₀ — соответственно квант. выход люминесценции и время жизни молекул донора на возбуж­дённом уровне энергии в отсутствии П. э.,  — фактор, зависящий от вза­имной ориентации молекул (в случае хаотичной ориентации ²=²/₃), n — показатель преломления среды, Л — расстояние между молекулами доно­ра и акцептора.

Влияние П. э. на макроскопич. хар-ки люминесценции можно определить, проведя усреднение по разл. R. Ре­зультат усреднения зависит от взаим­ного расположения совокупности моле­кул доноров и акцепторов и от его изменения в течение времени ₀. Если в течение этого времени молекулы мож­но считать неподвижными, то умень­шение числа доноров N(t) происходит по закону:



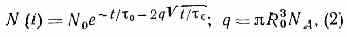
где R₀ — расстояние, на к-ром W=1/₀,N₀—число молекул донора, N_а — число молекул акцептора в 1 см³ в нач. момент времени t=0.

Ф-ла (2) справедлива для случая, когда концентрации молекул донора и акцептора сравнительно невелики, а среда оптически прозрачна. Если мо­лекулы донора и акцептора находятся в кристалле, имеющем собств. погло­щение в рассматриваемой спектр. области, то П. э. осуществляется вкситонами. Этот процесс можно обычно рассматривать как диффузию экситонов. Коэфф. диффузии D экситонов и, следовательно, эффективность П. э. в кристаллах зависят от того, являются ли экситоны «локализован­ными» (некогерентными) или свобод­ными (когерентными). В последнем случае D в достаточно совершенных кристаллах характерным образом зависит от темп-ры Т (D ~ T^-1/2), т. к. определяется рассеянием эксито­нов на фононах, число к-рых растёт с темп-рой.

•Галанин М. Д., Агранович В. М., Перенос энергии электронного воз­буждения в конденсированных средах, М., 1978.

М. Д. Галанин.

ПЕРЕНОСА ЯВЛЕНИЯ, необрати­мые процессы, в результате к-рых в физ. системе происходит пространств. перенос электрич. заряда, массы, им­пульса, энергии, энтропии или к.-л. другой физ. величины. П. я. описы­ваются кинетич. ур-ниями (см. Кине­тика физическая).

Причины П. я.— действие внеш. электрич. поля, наличие пространств.

неоднородностей состава, темп-ры или ср. скорости движения ч-ц систе­мы. Перенос физ. величины происхо­дит в направлении, обратном её гра­диенту, т. е. таким образом систе­ма приближается к состоянию равно­весия.

К П. я. относятся: электропровод­ность — перенос электрич. заряда под действием внеш. электрич. по­ля; диффузия — перенос в-ва (компо­нента смеси) при наличии в системе градиента его концентрации; тепло­проводность — перенос теплоты вслед­ствие градиента темп-ры; вязкое те­чение (см. Вязкость) — перенос им­пульса, связанный с градиентом ср. массовой скорости. Перенос в-ва вследствие градиента темп-ры: тер­модиффузию и обратный ей Дюфура эффект, гальваномагпитные явления и термогальваномагнитные явления — называют перекрёстными процессами, т.к. здесь гради­ент одной величины вызывает перенос др. физ. величины. При определ. ус­ловиях для перекрёстных процессов выполняется Онсагера теорема. При­ведённые примеры относятся к П. я. в гомогенных системах, внутри к-рых отсутствуют поверхности раздела.

П. я. происходят также в гетероген­ных системах, состоящих из гомоген­ных частей (подсистем), отделённых друг от друга или естеств. поверхнос­тями раздела (как жидкость и её пар), или полупроницаемыми мембра­нами.

При появлении в гетерогенной си­стеме разности (перепада) электрич. потенциалов, давлений, концентраций компонентов, темп-р между подси­стемами возникают необратимые по­токи заряда, в-ва компонентов и теп­лоты. К подобным П. я. относятся: электрокинетические яв­ления — перенос заряда и массы из-за перепада электрич. потенциала и дав­ления; фильтрация — перенос в-ва из-за перепада давления; термоеханические эффекты — перенос теплоты и массы из-за перепада темп-ры и давления, в частности механокалорический эффект — перенос теплоты, вызванный разно­стью давлений.

П. я. в газах изучает кинетическая теория газов на основе кинетического уравнения Больцмана для ф-ции рас­пределения ч-ц; П. я. в металлах — на основе кинетич. ур-ния для эл-нов в металлах; перенос энергии в непрово­дящих кристаллах — с помощью ки­нетич. ур-ния для фононов кристаллич. решётки.

Общую феноменологич. теорию П. я., применимую к любой системе (газообразной, жидкой или твёрдой), даёт термодинамика неравновесиях процессов. С 1950—60-х гг. теория П. я. интенсивно разрабатывается на основе неравновесной статистич. ме­ханики.

% См. лит. при ст. Термодинамика неравно­весных процессов.

Д. Н. Зубарев.

528


ПЕРЕНОСНОЕ ДВИЖЕНИЕ в меха­нике, движение подвижной системы отсчёта по отношению к системе от­счёта, принятой за основную (ус­ловно считаемую неподвижной). См. Относительное движение.

ПЕРЕОХЛАЖДЕНИЕ, охлаждение в-ва ниже темп-ры его равновесного перехода в др. агрегатное состояние T_ф.п. или в др. кристаллич. модифи­кацию (см. Полиморфизм). Фазовые переходы, связанные с отдачей теплоты (конденсация, кристаллизация, поли­морфные превращения) на нач. ста­дии, требуют, как правило, нек-рого П., содействующего возникновению зародышей новой фазы — мельчайших капель или кристалликов. Образо­вание зародышей при T._ф.п. затрудне­но тем, что они, обладая повыш. дав­лением или растворимостью, не могут находиться в равновесии с исходной фазой. В условиях, когда процессы возникновения и роста зародышей новой фазы протекают замедленно (перекристаллизация в тв. фазе, кри­сталлизация очень вязкой жидкости, напр. стекла, и др.), глубоким П. можно получить практически устой­чивую фазу (в метастабильном состоя­нии) со структурой, характерной для более высоких темп-р. На этом осно­ваны, напр., закалка сталей и полу­чение стекла. Следует также отме­тить, что степень П. водяного пара в атмосфере влияет на хар-р выпадаю­щих осадков (дождь, снег, град).

ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕ­НИЯ (коммутационные соотношения), фундаментальные соотношения в квант. теории, устанавливающие связь между последоват. действиями на волновую функцию (пли вектор состоя­ния) двух операторов (L₁ и L₂), рас­положенных в разном порядке (т. е. L₁L₂ и L₂L₁). П. с. определяют алгеб­ру операторов (q-чисел). Если два оператора переставимы (коммутиру­ют), т. е. L₁L₂=L₂L₁, то соответст­вующие им физ. величины L₁ и L₂ могут иметь одновременно определён­ные значения. Если же их действие в разном порядке отличается числовым фактором (с), т. е. L_iL₂-L₂L_l=c, то между соответствующими физ. ве­личинами имеет место неопределённос­тей соотношение L₁L₂¹/₂│c│, где L₁ и L₂ — неопределённости (дисперсии) измеряемых значений физ. величин l₁ и L₂. Важнейшими в квант. механике явл. П. с. между опе­раторами обобщённой координата q и сопряжённого ей обобщённого импуль­са р, qp-pq=iћ. Если оператор L не зависит от времени явно и переста­вим с гамильтонианом системы Н, 1. е. LH=HL, то физ. величина L (а также её ср. значение, дисперсия и т. д.) сохраняет своё значение во времени.

В квант. механике систем тождеств. ч-ц и квант. теории поля фундам. значение имеют П. с. для операторов

рождения (а⁺) и поглощения (а^-) ч-ц. Для системы свободных (невза­имодействующих) бозонов оператор рождения ч-цы в состоянии n, а⁺_n и оператор поглощения такой ч-цы an^-удовлетворяют П. с. а^-_n а⁺_n- а⁺_nа-_n=1, а для фермионое. a^-_na⁺_n+a⁺_n a^-_n=1; по­следнее П. с. явл. формальным выра­жением Паули принципа.

В. Б. Берестецкий.

ПЕРЕСЫЩЕННЫЙ ПАР, пар, давле­ние к-рого выше давления насыщенного пара при тех же условиях.

ПЕРЕХОДНОЕ ИЗЛУЧЕНИЕ, излу­чение эл.-магн. волн равномерно и прямолинейно движущейся заряж. ч-цей при пересечении ею границы раздела двух сред с разными показа­телями преломления. Предсказано в 1945 В. Л. Гинзбургом и И. М. Фран­ком, к-рые показали, что излучение должно возникать по обе стороны от границы раздела, и подсчитали энер­гию, излучаемую назад — в среду, из к-рой ч-ца выходит, пересекая гра­ницу, раздела. При движении заряж. ч-цы в однородной среде её поле пере­мещается вместе с ней; хар-р поля определяется скоростью ч-цы и св-вами среды. Когда ч-ца переходит в др. среду, её поле меняется, что сопровождается излучением эл.-магн. волн. Расчёты показали, что назад излучаются эл.-магн. волны видимого диапазона (независимо от скорости ч-цы), интенсивность этого излучения мала (примерно 1 фотон при пересе­чении границы раздела 100 ч-цами). При малых энергиях ξ ч-цы энергия, теряемая ею при П. и. назад, растёт пропорц. ξ, при высоких ξ рост за­медляется.

Первое сообщение об эксперим. об­наружении П. и. назад появилось в 1958. П. и. от пучка ч-ц, падающего на металлич. поверхность в вакууме, наблюдается визуально в виде яркого белого светящегося пятна в том месте, куда падает пучок. Хар-ки П. и., полученные экспериментально, ока­зались в хорошем согласии с теорией. С развитием эксперим. методов изме­рения определение П. и. в оптич. области стало настолько точным, что по его параметрам (спектру, поляри­зации, угл. распределению) можно судить об оптич. св-вах поверхностей.

Исследования П. и. вперёд пока­зали, что при больших значениях ξ энергия этого излучения пропорц. ξ, а распространяется оно под очень малыми (обратно пропорц. ξ) углами к направлению движения ч-цы. Ча­стота П. и. вперёд (в отличие от П. и. назад) занимает очень широкую спектр. область, причём макс. частота про­порц. ξ. Напр., эл-н с ξ=10 ГэВ, пересекающий границу раздела плот­ной среды и газа, излучает вперёд фотон с энергией ~10 КэВ.

Линейный рост потерь на П. и. с увеличением ξ позволяет использо­вать его для определения энергии быстрых заряж. ч-ц. В счётчиках,

действие к-рых основано на П. и., ч-ца пересекает ок. 1000 слоев в-ва, разделённых газовыми проме­жутками, и суммарное П. и. регистри­руется к.-л. приёмником излучения. Пластинки в-ва можно заменить по­ристым в-вом, напр. пенопластом. Счётчики на П. и. позволяют опреде­лить хар-ки заряж. ч-ц очень больших энергий (напр., в косм. лучах), когда др. методы регистрации теряют эффек­тивность.

П. и. на одной границе раздела пред­ставляет собой частный случай излу­чения, возникающего при движении заряж. ч-ц в неоднородной среде. Излучение, возникающее в сильно неоднородной среде, в принципе также может быть использовано для детек­тирования заряж. ч-ц. П. и. может быть использовано также для опреде­ления св-в среды (плотности, периода кристаллич. решётки и т. д.). При движении быстрых заряж. ч-ц П. и. неотделимо от Черенкова — Вавилова излучения.

• Гинзбург В. Л., Франк И. М., Излучение равномерно движущегося элект­рона, возникающее при его переходе из од­ной среды в другую, «ЖЭТФ», 1946, т. 16, в. 1; Гарибян Г. М., К теории переход­ного излучения и ионизационных потерь энергии частицы, там же, 1959, т. 37, в. 2, с. 527; Барсуков К. А., Переходное излучение в волноводе, там же, в. 4, с. 1106; Тер-Микаелян М. Л., Влияние сре­ды на электромагнитные процессы при высо­ких энергиях, Ереван, 1969.

Б. М. Болотовский.

ПЕРЕХОДНЫЕ МЕТАЛЛЫ, химич. элементы I6 и VIIIб подгрупп периодич. системы элементов. В П. м. внутр. оболочки атомов заполнены только частично. Различают d-металлы, у к-рых происходит постепенное заполнение З-d (от Sc до Ni), 4-d (от Y до Pd) и 5-d (от Hf до Pt)-подоболочек, и f-металлы, у к-рых заполняются 4f-подоболочки (редкие земли, или лантаноиды, от Се до Lu) и 5f-подоболочки (актиноиды). Ряд актиноидов начинается с Ас. У Th и последующих элементов заполняется 5f-оболочка. Все актиноиды радиоак­тивны. Общее число П. м. 61. У меди, когда она двухвалентная, 3d-оболочка не совсем заполнена. Поэтому в CuO ион Cu⁺ ведёт себя как ион П. м. На этом основании Cu, Ag и Au (метал­лы la подгруппы) условно также мож­но считать П. м. Особенности строе­ния электронных оболочек атомов определяют нек-рые специфич. св-ва П. м.: парамагнетизм, ферромагне­тизм, антиферромагнетизм, сверх­проводимость, способность к комп­лектованию, аномалию в изменении таких хар-к межатомной связи в ре­шётке, как упругие константы, теп­лота сублимации и темп-pa плавления, при увеличении ат. номера элемента. •Уманский Я. С., С к а к о в Ю. А., Физика металлов, М., 1978; В о н с о в с к и й С. В., И 3 ю м о в Ю. А., К у р м а е в Э. З., Сверхпроводимость переход­ных металлов, их сплавов и соединений, М., 1977. Б. Я. Любое.

529


ПЕРИОД КОЛЕБАНИЙ, наимень­ший промежуток времени, через к-рый .система, совершающая колебания, снова возвращается в то же состояние, в к-ром она находилась в нач. момент, выбранный произвольно. Строго гово­ря, понятие «П. к.» применимо лишь, когда значения к.-л. величины точно повторяются через одинаковые про­межутки времени, напр. в случае гар­монических колебаний. Однако поня­тие «П. к.» часто применяется и для приблизительно повторяющихся про­цессов.

ПЕРИОД ПОЛУРАСПАДА, промежу­ток времени, в течение к-рого исход­ное число радиоактивных ядер в сред­нем уменьшается вдвое. При наличии N₀ радиоактивных ядер в момент времени t=0 их число N убывает во времени по закону: N=N₀e^-t, где  — постоянная радио­активного распада. Ве­личина =1/ наз. ср. временем жиз­ни радиоактивных ядер. П. п. T_1/2 связан с  и  соотношением: T_1/2=ln2 = 0,693/.

• См. лит. при ст. Радиоактивность.

ПЕРИОДИЧЕСКАЯ СИСТЕМА эле­ментов Д. И. Менделеева, система элементов, к-рая отражает периодич. закон Менделеева — периодич. за­висимость физ. и хим. св-в элементов от их ат. веса (в совр. формулиров­ке — от заряда ат. ядер элементов, равного ат. номеру элемента в П. с.). Так, элементы с порядковыми номе­рами Z=2, 10, 18, 36, 54 и 86 (разно­сти ат. номеров 8, 8, 18, 18, 18) обла­дают сходными физ. и хим. св-вами и явл. инертными газами; элементы с Z=Z, 11, 19, 37, 55 и 87 — химиче­ски активные лёгкие металлы, реаги­рующие с галогенами и образующие с ними ионные кристаллы.

В 1869 Менделеев, расположив эле­менты в порядке возрастания ат. веса и сгруппировав элементы с аналогич­ными св-вами, предложил первую П. с. Разработанная им в 1871 «короткая форма периодич. таблицы», сходная с совр. П. с. элементов, получила широкое признание в 80-х гг., после того как были найдены нек-рые пред­сказанные Менделеевым элементы (в табл. для них были оставлены незаполненные клетки). Новое разви­тие П. с. получила после открытия в кон. 19— нач. 20 вв. радиоактивности. В 1913 англ. учёный Ф. Содди уста­новил изотопию хим. элементов и по­казал, что именно по этой причине ат. веса имеют нецелочисленные значе­ния; в том же году англ. физик Г. Мозли разработал эксперим. методы опре­деления заряда ядер. Эти открытия окончательно подтвердили правиль­ность расположения элементов в П. с. и вызвали к жизни термин «ат. номер» и новую формулировку периодич. за­кона. Полное науч. объяснение П. с. по­лучила на основе квантовой механики.

Все известные хим. элементы обра­зуют 8 вертикальных столбцов групп (см. таблицу на форзаце), обозначаемых вверху римскими циф­рами, причём все группы содержат 2 подгруппы (напр., VII группа делит­ся на подгруппы марганца и галоге­нов). Номер группы в П. с. соответст­вует высшей положит. валентности элемента. Св-ва элементов в группах и подгруппах с ростом ат. номера из­меняются закономерно. Так, в под­группе щелочных металлов (1а) уве­личение Z сопровождается повыше­нием хим. активности, тогда как в под­группе галогенов (VIIa) наблюдает­ся обратная картина.

Горизонтальные ряды П. с. назы­вают периодами (их всего 7) и обоз­начают арабскими цифрами. Внутри каждого периода наблюдается б. или м. равномерный переход от активных металлов, через менее активные ме­таллы и слабоактивные неметаллы к очень активным неметаллам и, нако­нец, к инертным газам.

В каждом периоде, начиная с 4-го, между II и III группой находятся ряды переходных элементов • - ме­таллов со сходными хим. св-вами; 15 переходных элементов 6-го периода, практически неразличимые по св-вам, наз. лантаноидами (или редкоземель­ными элементами). Аналогичный ряд очень сходных металлов — актинои­дов имеется в 7-м периоде.

Структура П. с. полностью отве­чает порядку заполнения электрон­ных оболочек и слоев (см. Атом). Число хим. элементов в периоде равно числу эл-нов в слое, к-рое строго определено в соответствии с Паули принципом, запрещающим существо­вание в атоме эл-нов в одинаковом квант. состоянии. Состояние эл-на определяется 4 квант. числами: глав­ным квант. числом n=1, 2, 3, . . ., орбитальным квант. числом l=0, 1, . . ., n-1, магн. квант. числом m_l=0, ± 1, ± 2, . . ., ±l и спиновым квант. числом m_s=±¹/₂. Каждому значению l соответствуют (2l+1) значений m_l, а каждому значению m_l — два воз­можных значения m_s. Т. о., замкнутая оболочка, характеризуемая определ. значением l, содержит 2(2l+1) эл-нов. Макс. число эл-нов в слое с определённым n равно 2^l=n-1_l=0(2l+1).

Т. о., замкнутая s-оболочка (l=0) содержит 2 эл-на, р-оболочка (s=1) — 6 эл-нов, d-оболочка (Z=2) — 10 эл-нов и т. д. Число же эл-нов в слоях (число элементов в периодах П. с.). , соответ­ствующих n=1, 2, 3, . . ., 7 состав­ляет 2, 8, 8, 18, 18, 32, 32.

Св-ва атомов элементов определя­ются числом эл-нов во внеш. оболочке, поэтому элементы, имеющие одинако­вое строение внешней оболочки, при­надлежат к одной группе П. с. Эле­менты с замкнутыми внешними обо­лочками явл. инертными газами. По­рядок заполнения электронных оболочек следует порядку расположе­ния уровней энергии с данными n и l. Для лёгких элементов это соот­ветствует заполнению сначала слоя с меньшим, а затем с большим значе­нием n; внутри слоя сначала заполня­ется s-оболочка, затем р-оболочка и т. д. Однако в группах переходных элементов от Sc до Ni (ат. номера 21 — 28), от Y до Pd (ат. номера 39—46), от La до Pt (ат. номера 57—78) и от Ас до No (ат. номера 89—102) этот порядок нарушается, поскольку со­стояния с большими значениями n имеют меньшую энергию, чем ещё не занятые состояния с меньшими n.

• См. лит. при ст. Атом.

В. Г. Дашевский.