П падение тела

Вид материала

Документы

Содержание А. С. Вольмир. Пластическая деформация Пластичности теория Физические основы П. т. Рис. 1. График, изображающий процесс де­формации трубчатого образца. К — модуль объёмной упругости (см. Модули упругости),  Рис. 3. Графики процессов с одинаковой внутренней геометрией k(s). ON и по­верхности текучести F А. А. Ильюшин, В. С. Ленский.

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПЛАНКА ПОСТОЯННАЯ (квант дей­ствия, обозначается h), фундаменталь­ная физ. константа, определяющая широкий круг физ. явлений, для к-рых существенна дискретность величин с размерностью действия (см. Квантовая механика). Введена нем. физиком М. Планком в 1900 при установлении за­кона распределения энергии в спектре излучения абсолютно чёрного тела (см. Планка закон излучения). Наиб. точное значение П. п. получено на ос­нове Джозефсона эффекта: h=6,626176 (36) •10^-34 Дж•с=6,626176(36)•10^-27 эрг•с (на 1977). Чаще пользуются постоянной ћ=h/2=1,0545887 (57)•10^-34 Дж•с, также называемой П. п.

ПЛАСТИНКИ, тела, имеющие форму прямой призмы или прямого цилинд­ра, высота к-рого (толщина) мала по сравнению с размерами основания. По очертанию основания П. делятся на прямоугольные, круглые, эллиптиче­ские и т. д. Плоскость, к-рая делит толщину П. пополам, наз. срединной плоскостью.

П. широко применяются в технике как элементы многих конструкций и сооружений; в акустике П. использу­ются в качестве элементов излучателей и приёмников звука, преград в звуко­вом поле и др.

В зависимости от характера дейст­вующих на П. нагрузок различают П., работающие на изгиб при поперечной нагрузке и на растяжение — сжатие при нагрузке, действующей в средин­ной плоскости.

При деформации изгиба точки П. по­лучают перемещения (прогибы), пер­пендикулярные к срединной плоскос­ти. Поверхность, к-рую образуют точ­ки срединной плоскости после дефор­мации, наз. срединной поверхностью. В зависимости от характера деформа­ции срединной поверхности при изгибе П. подразделяют на жёсткие, или мало­го прогиба (не более ¹/₅ толщины), гибкие (прогиб от ¹1₅ до 5 толщин) и абсолютно гибкие, или мембраны (при прогибе св. 5 толщин).

В жёсткой П. без заметной погреш­ности можно считать её срединный слой при поперечной нагрузке нейтраль­ным, т. е. свободным от напряжений растяжения — сжатия. При расчёте жёстких П. пользуются, как правило, гипотезой прямых нормалей, согласно к-рой любая прямая, нормальная к срединной плоскости до деформации, остаётся и после деформации прямой, нормальной к срединной поверхности, а длина волокна вдоль толщины П. счи­тается неизменной.

В гибкой П. (при расчётах в преде­лах упругости) наряду с чисто изгибными напряжениями необходимо учи­тывать напряжения, равномерно рас­пределённые по толщине пластинки. Последние наз. цепными (или мембран­ными) напряжениями или напряжени­ями в срединной поверхности. В абсо­лютно гибкой П., или мембране, при исследовании упругих деформаций можно пренебречь собственно изгибными напряжениями по сравнению с напряжениями в срединной поверх­ности.

При работе П. под нагрузкой, дейст­вующей в срединной плоскости, на­пряжения распределяются равномер­но по толщине, т. е. П. работает в ус­ловиях более выгодных, чем в случае поперечной нагрузки. Однако при атом возможна потеря устойчивости П. (см. Устойчивость упругих систем), и её обычно приходится подкреплять сетью рёбер жёсткости.

Важное значение имеет расчёт сво­бодных и вынужденных колебаний П, (т. н. динамич. задачи).

544


• Бубнов И. Г., Труды. по теории пла­стин, М., 1953; Тимошенко С. П., Войновский-Кригер С., Пластин­ки и оболочки, [пер. с англ.], 2 изд., М., 1966; Вольмир А. С., Гибкие пластин­ки и оболочки, М., 1956; его же, Нели­нейная динамика пластинок и оболочек, М., 1972.

А. С. Вольмир.

ПЛАСТИНКИ в акустике, использу­ют в качестве колебат. систем — эле­ментов излучателей и приёмников, а также звуковых преград. П. подразде­ляют на тонкие и толстые по сравне­нию с длиной упругих волн в них. В тонких П. возможны поперечные ко­лебания (изгиба) и продольные коле­бания (растяжения), когда смещения ориентированы в плоскости П. Изгиб в тонких П. не сопровождается растя­жением её срединной плоскости, поэто­му колебания изгиба и растяжения мо­гут существовать независимо друг от друга. В толстых П. это не имеет мес­та. Колебания таких П. можно пред­ставить как совокупность продольных и сдвиговых волн, распространяющих­ся в толще П. и отражающихся на обеих её сторонах. В соответствии с двумя типами коле­баний в неограниченной (бесконечной) тонкой П. могут распространяться продольные и поперечные волны. Ско­рость продольных волн в тонкой П. не зависит от длины волны. Для попе­речных (изгибных) волн П. явл. сис­темой, обладающей дисперсией волн. П. ограниченного размера обладает дискр. рядом собств. частот. Каждой собств. частоте соответствует своя собств. форма колебаний, наглядно представляемая расположением узло­вых линий, где смещения в процессе колебаний равны нулю. Собств. часто­ты и формы колебаний зависят от раз­меров и формы П., упругости и плот­ности её материала, а также от усло­вий закрепления её краёв (см. Хладни фигуры). Колеблющаяся П. излучает волны в окружающую среду. Эффек­тивность излучения П. зависит от уп­ругости и плотности материала П., а также от св-в среды, в к-рой она нахо­дится.

ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ, см. Деформация механическая.

ПЛАСТИЧЕСКИЙ ШАРНИР, попе­речное сечение балки или полосы, полностью находящейся в идеально пластич. состоянии. Понятие «П. ш.»



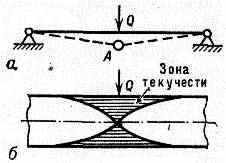
а — Образование пластич. шарнира; б — сечение балки в области пластич. шар­нира А.

приобрело большое значение в связи с исследованием несущей способности стержневых и рамных конструкций. П. ш. возникает в наиболее напря­жённых сечениях. Напр., если шарнирно опёртая балка (см. рис.) нахо­дится под действием сосредоточенной силы Q, то при увеличении этой силы П. ш. образуется в окрестности сече­ния, в к-ром возникает наибольший изгибающий момент. Образование П. ш. уменьшает степень статич. неопре­делимости конструкции и может сде­лать её статически определимой или даже геометрически изменяемой.

ПЛАСТИЧНОСТИ ТЕОРИЯ, раздел механики, в к-ром изучаются законы, отражающие связи между напряжени­ями и упругопластич. деформациями (физ. основы П. т.), и разрабатываются методы решения задач о равновесии и движении деформируемых тв. тел (матем. П. т.). П. т. явл. основой совр. расчётов конструкций, сооружений и машин с учётом макс. использования прочностных и деформац. ресурсов ма­териалов, а также расчётов технологич. процессов обработки металлов давлением (ковки, штамповки и др.) и ряда природных процессов (горооб­разования, дрейфа континентов и др.).

Упругие деформации конструкц. ма­териалов имеют величину 0,3—0,5%, тогда как пластич. деформации до разрушения достигают значений 10— 20% и более, а напряжения при раз­рушении превышают предел текучести в неск. раз. Поэтому методы расчёта, основанные на допустимости только упругих деформаций, не всегда техни­чески и экономически целесообразны. Более того, иногда создание жизне­способной конструкции просто не­возможно без учёта стадии пластич. деформации.

Физические основы П. т. Физ. ос­новой П. т. явл. законы связи между напряжениями и деформациями (см. Пластичность) в разл. термомеханич. условиях. Для пластичности типично, что значения напряжений зависят не только от текущих значений деформа­ций, но и от предшествующего процес­са их изменения. Напр., если тонко­стенный трубчатый образец вначале растянуть до относит. удлинения ₁, а потом при неизменном ₁ закрутить до деформации сдвига _1; то в конце этого процесса норм. и касат. напря­жения в поперечном сечении образца достигают нек-рых значений ₁₁. Если такой же образец вначале закрутить до той же деформации сдвига ₁, а по­том при постоянном ₁ растянуть до относит. удлинения ₁, то в этом про­цессе норм. и касат. напряжения до­стигают значений '₁'₁, отличных от ₁₁.

В общем случае процесс деформации описывается шестью ф-циями измене­ния компонентов тензора деформации (см. Деформация механическая), одна­ко его удобно также представлять гра­фически. Напр., при совместном рас­тяжении и кручении трубчатого об­разца деформированное состояние изображается в прямоугольной системе координат O_э1э2 точкой М (рис. 1), ко­ординаты к-рой по оси э₁=, а по оси

э₂=/3 (множитель 1/3 вводит­ся в связи с тем, что предел текучести при растяжении в 3 раз отличается от предела текучести при сдвиге), или

вектором деформации э=ОМ. Модуль вектора э равен интенсивности дефор­мации _u. В процессе деформации точ­ка М (э₁, э₂) очерчивает кривую OL, к-рая наз. т р а е к т о р и е й д е ф о р м а ц и и. Степень сложности процесса характеризуется кривизной траектории деформации k, к-рая явл. ф-цией длины дуги s траектории: k=k(s).



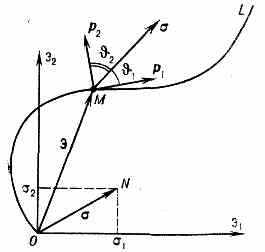
Рис. 1. График, изображающий процесс де­формации трубчатого образца.


Эта функция определяет т. н. внутреннюю геометрию траектории. Деформация наз. п р о с т о й, если все компоненты тензора деформации возрастают пропорционально одному параметру (напр., времени или длине дуги s). Траектория простой дефор­мации — прямолинейный луч ОК (рис. 2); её кривизна k(s)=0, причём s=_u. При сложной деформации k(s)0 (кривая OL). Частный случай сложной деформации — двухзвенный процесс, изображаемый ломаной (напр., OCD).

Напряжённое состояние можно изоб­ражать на плоскости (э₁, э₂) в виде вектора напряжений =ON^ (рис. 1) с координатами ₁=, ₂=3. Начало этого вектора отно­сят к той точке траектории деформа­ции, в к-рой это напряженное состоя­ние достигнуто. Если в одном образце точка М достигнута путём процесса OL (рис. 2), а в другом, идентичном, путём процесса OL', то векторы на­пряжений  и ' в этой точке различ­ны.

Зависимость нек-рой величины в мо­мент t от процесса изменения другой величины в интервале (0, t) описывает­ся матем. объектом, к-рый наз. функ­ционалом. При пластич. дефор­мации напряжения — функционалы процесса деформации, а также давле­ния, темп-ры и скорости деформации.

Теория малых у п р у г о п л а с т и ч е с к и х д е ф о р м а ц и й. При простой активной деформа­ции, когда интенсивность деформации _u возрастает, имеют место соотноше-

545


ния теории малых упругопластич. де­формаций (А. А. Ильюшин, 1943):



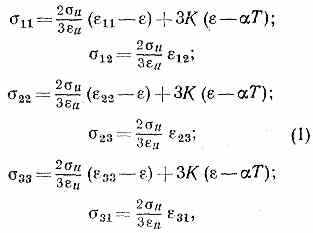
к-рые означают, что а) вектор напря­жений коллинеарен лучу деформации (_A на рис. 2); б) его модуль— функ­ция _u, давления q, темп-ры Т и скорости изменения интенсивности дефор­мации _u=d_u/dt, не зависящая от на­правления луча деформации; в) отно­сит. изменение объёма =3=₁₁+₂₂+₃₃ пропорционально среднему напряжению =¹/₃(₁₁+₂₂+₃₃) и темп-ре.



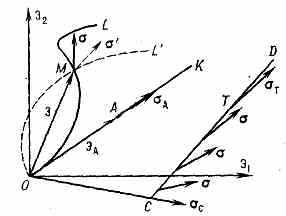
Рис. 2. Траектории деформации: ОК — при простой деформации, k(s)=0; OL — при произвольном сложном процессе, k(s)0; OCD — двухзвенный процесс кру­чения трубчатого образца при постоянном удлинении; k(s)=0 всюду, кроме точки С, где k(s)=.


Здесь К — модуль объёмной упругости (см. Модули упругости),  — коэфф. линейного теплового рас­ширения, _u=Ф(_u, q, Т, _u) — экс­периментально определяемая ф-ция, к-рая при неизменных q, Т и _u наз. ф у н к ц и е й у п р о ч н е н и я. При пассивной деформации (_u убы­вает), т. е. при разгрузке, приращения напряжений и деформаций связаны соотношениями обобщённого Гука за­кона. Теория малых упругопластич. деформаций используется в практике расчётов конструкций и сооружений на прочность и устойчивость при пластич. деформациях.

Теория течения С е н-Ве н а н а. Франц. учёный А. Сен-Венан (1871) предположил, что в слож­ном процессе активной деформации идеально пластич. (неупрочняющегося) материала, для к-рого интенсивность напряжений _u постоянна и равна пределу текучести _s при активной пластич. деформации, вектор напря­жений коллинеарен касательной к траектории деформации и материал меха­нически несжимаем. При изотермич. условиях соотношения напряжения — деформации по его теории имеют вид



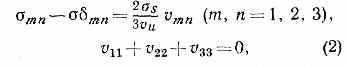
где v_mn — компоненты тензора скоро­стей деформации, v_u — интенсивность скоростей деформации, _mn — символ Кронекера: _mn=1 при т=п и _mn=0 при mn. Соотношения (2) хорошо согласуются с данными опытов только при простой деформации и в процес­сах малой кривизны (см. ниже). Тео­рия течения Сен-Венана успешно ис­пользуется при расчётах технологич. процессов формоизменения неупроч­няющихся или слабоупрочняющихся металлов (штамповки, прессования и др.). При расчётах горячих скоростных процессов необходимо учитывать зави­симость _s от темп-ры и скорости деформации.

При сложном процессе деформации к построению соотношений между на­пряжениями и деформациями имеется несколько подходов.

Теория упругопластических процессов. При сов­местном растяжении и кручении труб­чатого образца вектор напряжений можно представить в виде =_uX(p₁cos₁+p₂cos₂), где единичные векторы касательной р₁ и нормали р₂ к траектории деформации образуют т. н. репер Ф р е н е, а ₁ и ₂ — углы ориентации вектора напряжений, т. е. углы между а и р₁ и p₂ соответственно

(рис. 1), причём ₂=/2-₁. Если ве­личины _u и ₁ определены как функции процесса (функционалы), то написанное выражение для о даёт связь между напряжениями и дефор­мациями.

В общем случае сложного напря­жённого состояния процесс изменения девиатора деформации изображается в пятимерном пространстве траектори­ей деформации, внутр. геометрия к-рой описывается кривизнами k₁(s), k₂(s), k₃(s), k₄(s), а репер Френе определяется пятью единичными векторами р₁, p₂, p₃,,p₄, p₅. Параметрами, определяю­щими процесс деформации, явл.: ори­ентация траектории, её внутр. геомет­рия (кривизны), давление q, темп-pa Т и скорость деформации s=ds/dt, за­данные как ф-ции длины дуги s. Век­тор напряжений а определяется моду­лем ||= _u и углами ориентации:



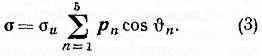
Задачей теории явл. установление за­висимости величин _u, ₁, ₂, ₃, ₄, ₅ от параметров произвольного процесса деформации.

Осн. законом теории упругопластич. процессов явл. постулат изотропии А. А. Ильюшина, согласно к-рому для изотропного материала модуль вектора напряжении и углы его ориентации в репере Френе однозначно определя­ются изменением параметров процесса от его начала до текущего момента, т. е. они явл. функционалами, порождае­мыми ф-циями k₁(s), k₂(s), k₃(s), k₄(s), q(s), T(s), s(s), и не зависят от ориен­тации траектории деформации. Дейст­вительно, в опытах обнаружено, что если в трёх одинаковых образцах из изотропного материала, испытывае­мых, напр., при совместном растяже­нии и кручении, осуществить процессы деформации OL, OL', OL" (рис. 3) с одинаковой внутренней геометрией k(s)=k'(s)=k"(s) (траектория OL' по­строена путём отражения OL в нек-ром луче ОА, а траектория OL" -- пово­ротом OL на нек-рый угол), то в точках М, М', М" с одинаковыми значениями длины дуги (ОМ=ОМ'=ОМ") модули векторов напряжений и углы их ори­ентации одинаковы: _u='_u="_u; =₁. Т. о., равенство (3) даёт об­щий вид зависимости между напряже­ниями и деформациями при произволь­ном процессе нагружения. Определе­ние функционалов пластичности по данным опытов чрезвычайно затрудни­тельно и пока предложены способы построения лишь части из них.




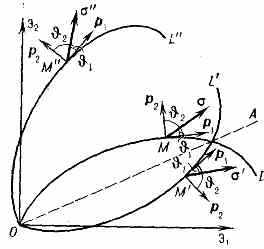
Рис. 3. Графики процессов с одинаковой внутренней геометрией k(s).

Другое фундаментальное св-во пла­стичности изотропного материала от­ражает принцип запаздывания: значе­ния углов ориентации вектора напря­жений в репере Френе зависят от из­менения кривизн не на всей предшест­вующей траектории деформации, а лишь на последней её части, длина к-рой, характерная для данного мате­риала, наз. с л е д о м з а п а з д ы в а н и я. Это св-во позволило выде­лить неск. типов процессов (простой деформации, малой кривизны, средней кривизны, двухзвенных), для к-рых соотношения между напряжениями и упругопластич. деформациями уста­новлены конкретно и не содержат фун­кционалов.

Т е о р и я т е ч е н и я. Тензор напряжений _ij представляется в ше­стимерном пространстве точкой нагру­жения N, или вектором напряжений

=ON. В процессе нагружения _ij(t) точка N очерчивает траекторию нагру­жения (рис. 4). Деформация представ­ляется в виде суммы упругой и плас-

546


тической. Упругая часть деформации связана с напряжениями обобщённым законом Гука. Все напряжённые со­стояния, к-рые могут быть достигнуты из начального состояния без возникно­вения пластич. деформаций, распола­гаются на нек-рой поверхности F, наз. начальной п о в е р х н о с т ь ю т е к у ч е с т и. При выходе точки нагружения N за пределы поверхности F (активный процесс, нагрузка) изме­няются величины упругой и пластич. деформации и форма поверхности теку­чести (процесс NN' и новая, мгновен­ная поверхность текучести F'). Если затем точка нагружения перемещается внутрь мгновенной поверхности теку­чести (процесс N'N"), то изменяется только упругая деформация, а пластич. деформация и поверхность текучести



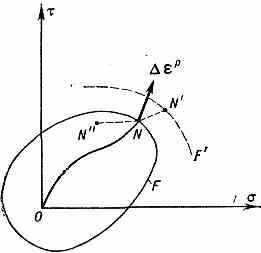
Рис. 4. Траектория нагружения ON и по­верхности текучести F для активного NN' и пассивного NN" процессов.

неизменны (пассивный процесс, раз­грузка). Конфигурация поверхности текучести явл. функционалом процес­са нагружения.

В основе теории течения лежит по­стулат пластичности, согласно к-рому работа напряжений на замкнутом цик­ле напряжений (деформаций), не мо­жет быть отрицательна, откуда следу­ет, что вектор скорости пластич. де­формации ^p направлен по нормали к мгновенной поверхности текучести в точке нагружения N. Это приводит к соотношениям:



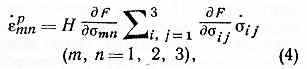
где ^p_mn — компоненты тензора плас­тич. деформации, точками сверху обоз­начены производные по времени. Т. н. функция упрочнения Н явл. функцио­налом предшествующего процесса нагружения и зависит от скоростей из­менения напряжений. Построить функ­ционал F практически невозможно, поэтому вводятся т. н. гипотезы упроч­нения, т. е. упрощающие предположе­ния об изменении поверхности теку­чести, а соотношения (4) линеаризу­ют, т. е. пренебрегают зависимостью Н от скоростей напряжений. В таком виде теория течения пригодна для ог­раниченного класса процессов.

Т е о р и я с к о л ь ж е н и я.

Этим термином объединяется ряд П. т.,

в к-рых рассматривается поликрист. агрегат (напр., металл). Для описа­ния пластичности отдельного зерна используется одна из простейших тео­рий пластичности (напр., теория иде­альной пластичности), Поликрист. аг­регат рассматривается как статистич. ансамбль с равновероятным распреде­лением форм и размеров зёрен, су­ществующих как бы в одной точке, и преимущественных плоскостей сколь­жений. Условия кинематич. и динамич. контакта между зёрнами учитываются не полностью. Путём статистич. ана­лиза разыскивается связь между на­пряжениями и деформациями в макро­объёме агрегата.

Математическая П. т. Матем. задача П. т. сводится к разысканию компо­нентов вектора перемещения, тензора деформации и тензора напряжений как ф-ций координат и времени, к-рые при заданных в объёмах тела массо­вых силах и темп-ре, усилиях на одной части граничной поверхности и пере­мещениях на другой части поверхно­сти должны удовлетворять дифф. ур-ниям движения (или равновесия), ур-ниям связи между деформациями и перемещениями, ур-ниям связи меж­ду напряжениями деформациями и темп-рой (законам пластичности), гра­ничным и нач. условиям. Система этих ур-ний составляет краевую задачу П. т.

Формулировка матем. задачи П. т. отличается от краевой задачи упруго­сти теории только тем, что соотноше­ния обобщённого закона Гука заменя­ются соотношениями той или иной П. т. При использовании теории идеальной пластичности (и др. теорий течения) вместо перемещений и де­формаций разыскиваются скорости ч-ц и тензор скоростей деформации. При использовании соотношений пластич­ности, относящихся к частным клас­сам процессов, требуется анализ физ. достоверности решения краевой зада­чи, т. к. в большинстве случаев не выяснены те условия нагружения тела произвольной формы, при к-рых во всех точках тела протекают процессы деформации определённого типа. В те­ории упругопластич. процессов дан общий метод установления физ. дос­товерности решений.

• Ильюшин А. А., Пластичность, ч. 1, .—Л., 1948; его же. Пластичность. Ос­новы общей математической теории, М., 1963; Соколовский В. В., Теория пластичности, 3 изд., М., 1969; X и л л Р., Математическая теория пластичности, пер. с англ., М., 1956.

А. А. Ильюшин, В. С. Ленский.