П падение тела

Вид материала

Документы

Содержание Просветления эффект Просвечивающий электрон­ный микроскоп Симметрия кристаллов) Пространственная дисперсия Пространственная инверсия Пространственная четность Пространство и время Пространство изображений Э. А. Тагиров.

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПРОСВЕТЛЕНИЯ ЭФФЕКТ, умень­шение скорости резонансного погло­щения при увеличении интенсивности падающего на среду эл.-магн. излу­чения. Причина П. э. — насыщение резонансного перехода (выравнива­ние населённостей уровней энергии). С увеличением интенсивности излу­чения заселённости уровней среды выравниваются. Величина поглоще­ния определяется в этом случае ско­ростью процессов релаксации, т. е. скоростью, с к-рой возбуждённый атом может передавать энергию возбужде­ния окружающей среде. Т. к. ско­рость релаксации определяется св-вами среды и не зависит от интенсивности падающего света, то с увеличением интенсивности излучения доля погло­щаемой в среде энергии уменьшается — переход насыщается.

Помимо описанного механизма, возможен и другой, связанный со сдвигом края полосы поглощения в коротковолновую область. При этом насыщаются края зон, т. е. заполня­ются уровни вблизи дна зоны прово­димости и потолка валентной зоны (см. Твёрдое тело). Такой механизм просветления характерен, в частности, для цветных стёкол.

Эффект просветления применяется в квант. электронике, где использу­ется для модуляции добротности ла­зерных систем, синхронизации мод лазеров, генерации узких линий и др. (см. Твердотельные лазеры).

• См. лит. при ст. Квантовая электроника, Лазер.

А. В. Андреев.

ПРОСВЕЧИВАЮЩИЙ ЭЛЕКТРОН­НЫЙ МИКРОСКОП, см. Электрон­ный микроскоп. ПРОСТРАНСТВЕННАЯ ГРУППА симметрии (Фёдоровская группа),

совокупность всех преобразований симметрии, присущих крист. решётке (см. Симметрия кристаллов) и сос­тавляющих с матем. точки зрения группу. Вывод всех 230 П. г. был осуществлён в 1890—91 Е. С. Фёдо­ровым и независимо от него нем. учёным А. Шёнфлисом. П. г. не ука­зывает конкретного расположения атомов в крист. решётке, но даёт один из возможных законов симметрии их взаимного расположения. Этим обу­словлена особая важность П. г. в структурной кристаллографии — любая из многих тысяч исследованных структур принадлежит к к.-л. одной из 230. Определение П. г. производит­ся рентгенографически (см. Рентге­новский структурный анализ). Все 230 П. г. табулированы в спец. спра­вочниках.

•См.. лит. при ст. Симметрия кристаллов.

ПРОСТРАНСТВЕННАЯ ДИСПЕРСИЯ, зависимость тензора диэлектрической проницаемости среды _ij(, k) от вол­нового вектора, обусловленная не­локальностью связи между электрич. индукцией D и напряжённостью элек­трич, поля E. Нелегальность связи D и E приводит к ряду явлений, наз. эффектами П. д., таких, как вращение плоскости поляризации, ани­зотропия кубич. кристаллов.

Вектор D(r) в к.-л. точке r среды не определяется однозначно величиной Е(r) в этой точке, а зависит также от значений Е(r') в соседних точках r', расположенных вблизи точки r. Та­кая нелокальность связи между D(r) и E(г) ясна, напр., из качеств. рассмотрения самой простой модели кристалла, согласно к-рой ч-цы, со­ставляющие крист. решётку (атомы, молекулы, ионы), совершают коле­бания около своего положения равно­весия и взаимодействуют друг с дру­гом. Электрич. поле световой волны смещает заряды из положения равно­весия, что вызывает дополнит. сме­щение зарядов в соседних и более уда­лённых ч-цах крист. решётки. По­этому поляризация среды P(r), a следовательно, и индукция D(r)=E(r)+4Р(r) зависят от значений напряжённости не только в одной выделенной точке, но и в её окрестно­сти. Это относится не только к кристал­лам, но и к изотропным средам, со­стоящим из асимметричных молекул. Размеры области взаимного влияния (а) составляют обычно величину по­рядка постоянной решётки (~10^-7 см) или размера молекул (для диэлектрич. сред). Длина световой волны  на неск. порядков превышает размеры этой области, поэтому на протяжении а значение поля световой волны су­щественно не меняется. Для описания взаимного влияния ч-ц достаточно представить электрич. поле в сосед­них точках r' в виде разложения в ряд Тейлора по степеням смеще­ний относительно точки r (x_j, x_l, x_m) и ограничиться первыми членами раз­ложения (x_j, x_l, x_m— декартовы ком­поненты вектора r). Тогда соотноше­ние между D и E можно записать в виде:



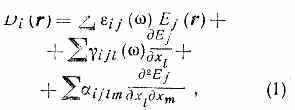
причем производные вычисляются в

точке r. Для плоской монохроматич.

волны, к-рую можно представить в

форме

D(r,t)=D₀exp[-i(t-kr)];

E(r, t)=E₀exp[ -i(t-kr)], (2)

где D₀ и E₀— пост. комплексные век­торы, a k — волновой вектор, имеем дE_i/дx_l=ik_lE_j. При учёте последнего выражение (1) приводится к виду

D_i(r)=_ij(, k)E_j(r, t), (3) где тензор _ij(, k) даётся соотноше­нием



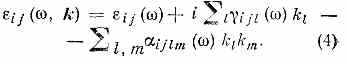
Т. о., в случае плоских монохрома­тич. волн связь между D(r, t) и Е (r, t} осуществляется тензором вто­рого ранга.

С первым членом выражения (4) свя­заны частотная дисперсия и двойное лучепреломление, обусловленное раз­личием показателей преломления обыкновенной n_o и необыкновенной n_e. волн (n_o/n_e~10^-1). Второй и третий члены выражения (4) пропорц. а/ и (а/)² (тензоры _ijl и _ijlm пропорц. соответственно и а и а²; k=2/). Если размер области взаимного влияния — 10^-7 см и 3•10^-5 см, то а/З•10^-3, а (а/)²~10^-5. Это очень малые величины, однако именно ими объясняются эффекты П. д. Если при­нять в расчёт только два первых члена в выражении (4) для _ij(, k), то

D (r, t)=()E(r, t)+i() [Е (r, t)k].

(5)

Вектор [Ek] перпендикулярен к E и k; множитель i указывает на сдвиг фазы второго члена в выражении (5) отно­сительно первого на /2. Второй член и приводит к различию фазовых ско­ростей (или показателей преломле­ния) для волн с правой и левой кру­говой поляризацией, т. е. к естеств. оптической активности — вращению плоскости поляризации и зависимости угла поворота от К.

В средах, обладающих центром, симметрии, величина () тождест­венно обращается в ноль и эффекты П. д. проявляются благодаря третье­му члену выражения (4). Эти слагае­мые обусловливают анизотропию ку­бич. кристаллов, имеющих центр сим­метрии, пропорциональную (а/)² и, следовательно, очень малую. Именно вследствие малости эффекта он был обнаружен экспериментально только в 1960 Е. Ф. Гроссом и А. А. Каплянским в кристалле закиси меди CuO₂, хотя на возможность этого эффекта указывал ещё голл. физик X. Лоренц, в 1878.

П. д. проявляется также в воз­можности распространения в кристал­лах не двух, а трёх или даже четырёх волн с разл. фазовыми скоростями. Добавочные световые волны, как по­казывают расчёты, могут быть суще­ственными при , близких к часто­там полос поглощения кристалла. До­бавочные волны возможны не только в кристаллах, но и в плазме. Теория

591


эффектов П. д. тесно связана с тео­рией экситонов. П. д. учитывалась при изучении таких вопросов, как аномальный скин-эффект в металлах, колебания крист. решётки и т. п.

• Гросс Е. Ф., Каплянский А. А., Оптическая анизотропия кубических крис­таллов, вызванная явлением пространствен­ной дисперсии, «ДАН СССР», 1960, т. 132, №1, с. 98; А г р а н о в и ч В. М., Г и н з б у р г В. Л., Кристаллооптика с учетом пространственной дисперсии и теория экси­тонов, 2 изд., М., 1979; Ландсберг Г. Л., Оптика, 5 изд., М., 1976 (Общий курс физики).

ПРОСТРАНСТВЕННАЯ ИНВЕРСИЯ (Р), изменение пространственных ко­ординат событий (x, у, z), опреде­лённых в нек-рой декартовой системе координат, на их противоположные значения: х-х, у-у, z-z (или r-r). Такое изменение можно трак­товать двояко: либо как активное преобразование — переход к сово­купности событий, являющихся зеркальным изображением данной сово­купности событий (изменение знаков координат к.-л. точки соответствует положению точки, полученной в ре­зультате её зеркального отражения в •трёх координатных плоскостях), либо как пассивное преобразование — опи­сание рассматриваемой совокупности событий в системе координат, полу­ченной из данной изменением на про­тивоположные направлений всех трёх координатных осей. Физ. смысл пре­образования П. и. связан с тем, что, как показывает опыт, процессы при­роды, обусловленные сильным и эл.-магн. вз-ствиями, симметричны отно­сительно этого преобразования. Это означает, что для всякого такого про­цесса в природе осуществляется и протекает с той же вероятностью «зер­кально симметричный» процесс. Сим­метрия относительно преобразования П. и. приводит при квантовомеханич. описании к существованию особой величины — пространств. чётности, к-рая сохраняется в процессах силь­ного и эл.-магн. вз-ствий. Слабое вз-ствие не обладает указанной сим­метрией, и в вызываемых им процес­сах чётность не сохраняется. Однако оно оказывается симметричным отно­сительно комбинированной инверсии,

С. С. Герштейн.

ПРОСТРАНСТВЕННАЯ ЧЕТНОСТЬ, чётность относительно операции про­странственной инверсии. См. Чёт­ность.

ПРОСТРАНСТВЕННОЕ КВАНТОВА­НИЕ, см. Квантование пространст­венное.

ПРОСТРАНСТВЕННЫЙ ЗАРЯД (объ­емный заряд), электрич. заряд, рас­средоточенный по нек-рому объёму. П. з. определяет пространств. рас­пределение электрич. потенциала и напряжённости электрич. поля. Для возникновения П. з. концентрации по­ложит. и отрицат. носителей заряда (напр., ионов и эл-нов в плазме)

не должны быть равны. Плотность П. з. =eZ_in_i (n_i — концентрация, eZ_i— заряд носителей сорта i). Т. к. образование объёмной статически рав­новесной системы из свободных заря­дов невозможно (см. Ирншоу теорема), появление П. з. обычно связано с прохождением электрич. тока. П. з. образуются вблизи электродов при прохождении тока через электролит, на границе двух ПП с различной (электронной или дырочной) проводи­мостью, в вакууме вблизи эмитирую­щего эл-ны катода, в газовом разряде вблизи электродов, стенок. Возникно­вению П. з. способствует различие коэфф. диффузии носителей заряда разных знаков. Поля, создаваемые П. з., в свою очередь определяют мн. важные св-ва газового разряда (раз­витие разряда во времени, образование стримеров и пр.), явлений в плазме (плазменные колебания и волны) и в ПП. Вследствие влияния П. з. плотность тока при движении эл-нов в вакууме с нулевой нач. скоростью на катоде меняется по закону «трёх вторых» (см. Ленгмюра формула). Ре­шение аналогичной задачи для поло­жит. ионов в газе зависит от характера движения ионов. Т. к.  есть алгебраич. сумма зарядов разных знаков, они могут частично или полностью компенсировать П. з. Примеры: плаз­ма с почти равными концентрациями эл-нов и ионов и прикатодная область в дуговом разряде, где в результате такой компенсации катодное падение потенциала невелико и почти не за­висит от тока.

ПРОСТРАНСТВО И ВРЕМЯ, катего­рии, обозначающие осн. формы су­ществования материи. Пр-во (П.) вы­ражает порядок сосуществования отд. объектов, время (В.) — порядок сме­ны явлений. П. и в.— осн. понятия всех разделов физики. Они играют гл. роль на эмпирич. уровне физ. позна­ния — непосредств. содержание ре­зультатов наблюдений и эксперимен­тов состоит в фиксации пространст­венно-временных совпадений. П. и в. служат также одними из важнейших средств конструирования теор. моде­лей, интерпретирующих эксперим. дан­ные. Обеспечивая отождествление и различение (индивидуализацию) отд. фрагментов материальной действитель­ности, П. и в. имеют решающее зна­чение для построения физ. картины мира. Св-ва П. и в. делят на м е т р и ч е с к и е (протяжённость и длитель­ность) и топологические (размерность, непрерывность и связ­ность П. и в., порядок и направление В.). Совр. теорией метрич. св-в П. и в. явл. теория относительности — спе­циальная (см. Относительности те­ория) и общая (см. Тяготение). Иссле­дование топологич. св-в П. и в. в физике было начато в 60—70-х гг. и пока не вышло из стадии гипотез. Историч. развитие физ. представле­ний о П. и в. проходило по двум на­правлениям в тесной связи с разл. философскими представлениями. В на­чале одного из них лежали идеи Де­мокрита, приписывающего пустоте особый род бытия. Они нашли наиб. полное физ. воплощение в ньютонов­ских понятиях абс. П. и абс. В. Со­гласно И. Ньютону, абс. П. и в. представляли собой самостоят. сущ­ности, к-рые не зависели ни друг от друга, ни от находящихся в них ма­териальных объектов и протекающих в них процессов. Др. направление развития представлений о П. и в. восходит к Аристотелю и было разра­ботано в философских работах нем. учёного Г. В. Лейбница, трактовавше­го П. и в. как определённые типы от­ношений между объектами и их изме­нениями, не имеющие самостоят. су­ществования. В физике концепция Лейбница была развита А. Эйнштей­ном в теории относительности.

Спец. теория относительности вы­явила зависимость пространств. и вре­менных хар-к объектов от скорости их движения относительно определён­ной системы отсчёта и объединила П. и в. в единый четырёхмерный п р о с т р а н с т в е н н о-в р е м е н н о й к о н т и н у у м — пространство-вре­мя (п.-в.). Общая теория относитель­ности вскрыла зависимость метрич. хар-к п.-в. от распределения тяготею­щих (гравитац.) масс, наличие к-рых приводит к искривлению п.-в. В об­щей теории относительности от ха­рактера распределения масс зависят и такие фундам. свойства п.-в., как конечность и бесконечность, к-рые также обнаружили свою относитель­ность.

Взаимосвязь св-в симметрии П. и в. с законами сохранения физ. величин бы­ла установлена ещё в классич. физике. Закон сохранения импульса оказался тесно связанным с однородностью П., закон сохранения энергии — с одно­родностью В., закон сохранения мо­мента кол-ва движения — с изотроп­ностью пр-ва (см. Сохранения законы, Симметрия законов физики). В спец. теории относительности эта связь обобщается на четырёхмерное п.-в. Общерелятивистское обобщение после­довательно провести пока не удалось.

Серьёзные трудности возникли так­же при попытке использовать выра­ботанные в классич. (в т. ч. реляти­вистской), т. е. неквантовой, физике понятия П. и в. для теор. описания явлений в микромире. Уже в нереляти­вистской квант. механике оказалось невозможным говорить о траекториях микрочастиц, и применимость поня­тий П. и в. к теор. описанию микро­объектов была ограничена дополни­тельности принципом (или неопреде­лённостей соотношением). С принци­пиальными трудностями встречается экстраполяция макроскопич. понятий П. и в. на микромир в квантовой тео­рии поля (расходимости, отсутствие объединения унитарной симметрии с пространственно-временными, теоре­мы Уайтмана и Хаага). С целью пре-

592


одоления этих трудностей был вы­двинут ряд предложений по модифика­ции смысла понятий П. и в.— кван­тование пространства-времени, из­менение сигнатуры метрики П. и в., увеличение размерности п.-в., учёт его топологии (геометродинамика) и др. Наиб. радикальной попыткой преодо­ления трудностей релятивистской квант. теории явл. гипотеза о неприменимости понятий п.-в. к микромиру. Аналогичные соображения высказы­ваются также в связи с попытками осмысления природы нач. сингуляр­ности в модели расширяющейся горя­чей Вселенной. Большинство физи­ков, однако, убеждены в универсаль­ности п.-в., признавая необходимость существ. изменения смысла понятий п.-в.

• Энгельс Ф., Диалектика природы, в кн.: Маркс К., Энгельс Ф., Соч., 2изд., т. 20; Л е н и н В. И., Материализм и эмпириокритицизм, Поли. собр. соч., 5 изд., т. 18; Эйнштейн А., Работы по теории относительности, [1905—1955], М., 1965 — 1966 (Собр. науч. трудов, т. 1—2); Фок В. А., Теория пространства, времени и тяготения, 2 изд., М., 1961; Грюнбаум А., Философские проблемы пространства и вре­мени, пер. с англ., М., 1969; Б л о х и н ц е в Д. И., Пространство и время в мик­ромире, М., 1970; Барашенков В. С., Проблемы субатомного пространства и вре­мени, М., 1979.

И. С. Алексеев.

ПРОСТРАНСТВО ИЗОБРАЖЕНИЙ в оптике, см. Изображение оптическое.

ПРОСТРАНСТВО ПРЕДМЕТОВ (объ­ектов) в оптике, см. Изображение оптическое,

ПРОТОН (от греч. protos — первый) (символ р), стабильная элем. частица, ядро атома водорода. Масса П. m_р=1,672614(14) •10^-24 г 1836 m_е, где m_е— масса эл-на; в энергетич. ед. m_p938,3 МэВ. Электрич. заряд П. положителен: е=4,803242(14) •10^-10 СГСЭ ед. заряда. Спин П. равен ¹/₂ (в ед. ћ,), поэтому П. подчиняются Ферми — Дирака статистике. Магн. момент П. равен: _р= 2,792763(30) _я, где _я— яд. магнетон. Вместе с нейтронами П. образуют ат. ядра всех хим. элементов, при этом число П. в ядре равно ат. номеру данного эле­мента и, следовательно, определяет место элемента в периодич. системе элементов Менделеева. Существует античастица по отношению к П.— антипротон.

К представлению о П. привели создание планетарной модели атома (англ. физик Э. Резерфорд, ,1911), открытие изотопов (англ. радиохимик Ф. Содди, англ. физики Дж. Дж. Томсон, Ф. Астон, 1906 — 19), ат. массы к-рых оказались кратными ат. массе водорода, эксперим. наблюдение ядер водорода, выбитых -частицами из ядер др. элементов (Резерфорд, 1919— 1920). Термин «П.» ввёл Резерфорд в нач. 20-х гг.

П. явл. адроном. Кроме сильного вз-ствия, он также участвует во всех др. фундам. вз-ствиях: эл.-магн., сла­бом и гравитационном. Он относится к классу барионов; его барионный за­ряд В=1. Законом сохранения барионного заряда определяется стабиль­ность П.— самого лёгкого из барионов; по эксперим. данным, ср. время жизни П. _р>10³⁰ лет. Модели т. н. «великого объединения» сильного, слабого и эл.-магн. вз-ствий предсказывают нару­шение закона сохранения барионного заряда и соотв. стабильности протона с _p~10³⁰—10³² лет.

В сильном вз-ствии П. и нейтрон имеют одинаковые св-ва и рассматри­ваются как два квант. состояния одной ч-цы — нуклона, к-рому приписыва­ется квант. число изотопич. спин I⁼¹/₂ (см. Изотопическая инвариант­ность). Важнейший пример сильного вз-ствия с участием П.— яд. силы, связывающие нуклоны в ядре. Общий подход в теор. объяснении св-в П. (напр., в процессах рассеяния) сво­дится к предположению о том, что П. окружён облаком виртуальных частиц, к-рые он непрерывно испу­скает и поглощает. Вз-ствие П. с др. ч-цами рассматривается как процесс обмена виртуальными ч-цами. Напр., яд. силы и низкоэнергетич. процессы объясняются в осн. обменом виртуаль­ным -мезоном между нуклонами. Эксперим. данные по рассеянию ч-ц высоких энергий (сотни МэВ и выше) объясняются участием в виртуальных процессах наряду с -мезонами др. адронов и образованием при опреде­лённых условиях резонансов в проме­жуточных состояниях.

Эл.-магн. св-ва П. неразрывно свя­заны с его участием в сильном вз-ствии. Пример этой связи — фоторождение мезонов, к-рое можно рассматривать как выбивание мезонов из облака вир­туальных адронов, окружающих П., -квантом (с энергией 150 МэВ). Вз-ствием П. с виртуальными -мезонами качественно объясняется боль­шое отличие магн. момента П. от яд. магнетона. Исследования рассеяния эл-нов и -квантов на П. позволили обнаружить пространств. распределе­ние электрич. заряда и магн. момента П. (амер. физик Р. Хофстедтер и др., 1957) и электрич. и магн. поляризуемостей П. (В. И. Гольданский и др., 1960) и т. о. получить свидетельство о наличии внутр. структуры П. Отли­чие эл.-магн. св-в П. от св-в точечной заряж. ч-цы описывается введением формфактора.

Примерами слабого вз-ствия с уча­стием П. явл. внутриядерные превра­щения П. в нейтрон и наоборот, прояв­ляющиеся в виде бета-распада ядер и электронного захвата.

Совр. объяснение структуры П. ос­новано на кварковой модели адронов, согласно к-рой Н. состоит из двух u-кварков и одного d-кварка, свя­занных обменом др. гипотетич. ч-ца­ми — глюонами (см. Кварки, Кван­товая хромодинамика, Элементарные частицы). Эксперим. данные по про­цессам с большой передачей импульса, напр. по глубоко неупругому процессу рассеяния эл-нов на П., свидетельству­ют о существовании внутри П. точечноподобных рассеивающих цент­ров — партонов. С точки зрения квар­ковой модели, партонами явл. кварки.

Ввиду стабильности П., наличия у него электрич. заряда и относит. простоты получения (ионизацией водо­рода) пучки ускоренных П. явл. од­ним из осн. инструментов эксперим. физики элем. ч-ц. Очень часто и ми­шенью в опытах по соударению ч-ц также явл. П.— свободные (водород) или связанные в ядрах. П. высокой энергии получают на ускорителях. Ускоренные П. используются не только для изучения рассеяния самих П., но также и для получения пучков ч-ц: я- и К-мезонов, антипротонов, мюонов. Пучки ускоренных П. использу­ются в лучевой терапии.

• Резерфорд Э., Избранные науч. труды. Строение атома и искусственное пре­вращение элементов, пер. [с англ.], М., 1972; Фейнман Р., Взаимодействие фотонов с адронами, пер. с англ., М., 1975; Ж а к о б М., Ландшофф П., Внутренняя структура протона, «УФН», 1981, т. 133, в. 3.

Э. А. Тагиров.