П падение тела

Вид материала

Документы

Содержание Потери магнитные В — магн. индукция, j ПОТОК ИЗЛУЧЕНИЯ (лучистый по­ток) Правой руки правило ПРАНДТЛЯ ТРУБКА (Пито—Пранд­тля трубка) Прандтля число Предел текучести Предельный цикл Фазовые портреты генератора Ван дер Поля при разл. значениях нелинейности: а — квазигармонич. колебания; б — сильно неси­нусоида М. И. Рабинович. Преломление света Стопа в оптике). Зависимость П. с. от поляризации падающих лучей нагляд­но проявляется при двойном лучепре­ломлении Преломления показатель Преломле­ние света). Дисперсия света). Преобразователи измеритель­ные В. П. Кузнецов.

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПОТЕРИ МАГНИТНЫЕ, электромагн. энергия, превращающаяся в теплоту в ферромагн. телах при периодич. перемагничивании их переменным магн. полем. П. м. Q за 1 цикл перемагничивания



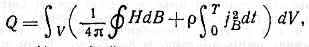
где V — объём перемагничиваемого тела, H — напряжённость магн. поля, В — магн. индукция, j_B — плотность вихревых токов,  — уд. электрич. сопротивление материала тела в физи­чески малом элементе dV его объёма (в ед. СГС). Первый интеграл в скоб­ках берётся по петле гистерезиса; он выражает потери на динамич. гистере­зис (последний может превышать ста­тический из-за магн. вязкости). Второй член в скобках определяет потери на вихревые токи, достаточно точный рас­чёт их возможен только в простейших случаях. Практически П. м. в магнитопроводах определяют эксперимен­тально.

• Кифер И. И., Испытания ферромаг­нитных материалов, 3 изд., М., 1969.

ПОТОК ИЗЛУЧЕНИЯ (лучистый по­ток), средняя мощность излучения за время, значительно большее периода колебаний; характеризуется кол-вом энергии, переносимой эл.-магн. вол­нами в единицу времени через к.-л. поверхность. Величину П. и. изме­ряют по его действию на неселектив­ный приёмник излучения. П о л н ы й п о т о к излучения можно измерить по его тепловому действию при погло­щении излучения приёмником в виде абсолютно чёрного тела.

Р е д у ц и р о в а н н ы й П. и.— мощность, оце­ниваемая по действию, вызванному излучением на спектрально-избира­тельный приёмник. Редуцированный П. и. может выражаться в спец. еди­ницах. Различают: световой поток Ф — поток, действующий на глаз; ф о т о а к т и н и ч н ы й — на фото­материалы и т. п. Осн. единица энер­гетич. П. и.— Вт, светового потока — лм. Соотношение между этими едини­цами наз. механическим эквивалентом света.

А. П. Гагарин.

ПРАВОЙ РУКИ ПРАВИЛО для оп­ределения направления индукц. тока в проводнике, движущемся в магн. поле: если расположить правую ладонь так, чтобы отставленный большой па-

лец совпадал с направлением движе­ния проводника, а силовые линии магн. поля входили в ладонь, то на­правление индукц. тока в проводнике совпадёт с направлением вытянутых пальцев. П. р. п. явл. следствием Лен­ца правила.

ПРАНДТЛЯ ТРУБКА (Пито—Пранд­тля трубка), прибор для одновремен­ного измерения полного и статич. дав­ления в потоке жидкости или газа. Представляет собой трубку Пито, усо­вершенствованную нем. учёным Л. Прандтлем (L. Prandtl), к-рый совме­стил измерение полного и статич. дав­ления в одном приборе. См. Трубки измерительные.

ПРАНДТЛЯ ЧИСЛО (по имени Л. Прандтля), один из подобия крите­риев тепловых процессов в жидкостях и газах Pr=v/a=c_р/, где v=/ — коэфф. кинематич. вязкости; [г — ко­эфф. динамич. вязкости;  — плотность;  — коэфф. теплопроводности; а=/c_р — коэфф. температуропроводности; c_р — уд. теплоёмкость сре­ды при пост. давлении.

П. ч. характеризует соотношение между интенсивностями мол. переноса кол-ва движения и переноса теплоты теплопроводностью; явл. физ. хар-кой среды и зависит только от её термоди­намич. состояния. У газов П. ч. с из­менением темп-ры практически не из­меняется (для двухатомных газов Pr0,72, для трёх- и многоатомных Prот 0,75 до 1). У неметаллич. жидко­стей П. ч. изменяется с изменением темп-ры тем значительнее, чем больше вязкость жидкости (напр., для воды при 0°С Pr=13,5, а при 100°С Pr=1,74; для трансформаторного масла при 0°С Pr=866, при 100°С Pr=43,9 и т. д.). У жидких металлов Pr<Pr=0,0115, при 700°С Pr=0,0039).

П. ч. связано с др. критериями по­добия — Пекле числом Ре и Рейнольдса числом Re соотношением Pr=Pe/Re.

С. Л. Вишневецкий.

ПРЕДЕЛ ТЕКУЧЕСТИ в сопротив­лении материалов, напряжение, при к-ром начинает развиваться пластич. деформация. В опытах с растяжением цилиндрич. образца определяется нор­мальное напряжение _s в поперечном сечении, при к-ром впервые возникают пластич. (необратимые) деформации. Аналогично, в опытах с кручением тонкостенного трубчатого образца оп­ределяется П. т. при сдвиге _s. Для большинства металлов _s=_s3.

В нек-рых материалах при непре­рывном удлинении цилиндрич. образ­ца на диаграмме зависимости нормаль­ного напряжения о от относит. удли­нения 8 обнаруживается т. н. зуб текучести, т. е. резкое снижение на­пряжения перед появлением пластич. деформации (рис., а), причём даль­нейший рост деформации (пластиче­ской) до нек-рого её значения проис­ходит при неизменном напряжении, к-рое наз. ф и з и ч е с к и м П. т. _т.

582


Горизонтальный участок диаграммы — наз. площадкой текучести; если её протяжённость велика, материал наз. идеально пластическим (неупроч­няющимся). В др. материалах, к-рые наз. упрочняющимися, площадки те­кучести нет (рис., б) и точно указать напряжение, при к-ром впервые возникают пластич. деформации, практи­чески невозможно.



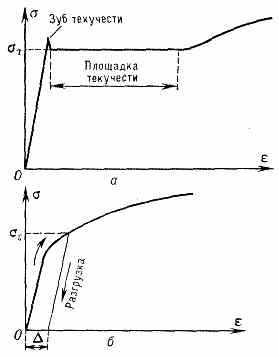
Вводится понятие условного П. т. _s как напряже­ния, при разгрузке от к-рого в образце впервые обнаруживается остаточная {пластич.) деформация величины Д. Остаточные деформации меньше  ус­ловно считаются пренебрежимо малы­ми. Напр., П. т., измеренный с допу­ском =0,2%, обозначается _0,2. См. также Пластичность.

В. С. Ленский.

ПРЕДЕЛЬНЫЙ ЦИКЛ, замкнутая изолированная траектория в фазовом пространстве динамич. системы, изоб­ражающая периодич. движение. В ок­рестности П. ц. фазовые траектории либо удаляются от него (неустойчивый П. ц.), либо неограниченно прибли­жаются к нему — «наматываются» на него (устойчивый П. ц.). Устойчивый П. ц. явл. матем. образом периодич. автоколебаний. Напр., уравнение Ван дер Поля (описывающее, в частности, динамику лампового генератора):

d²x/dt²-ξ(1-x²)dx/dt+х=0 имеет при зна­чении параметра нелинейности ξ>0 единственный устойчивый П. ц. (рис.). Для систем с одной степенью свободы (их фазовое пространство — плос­кость) устойчивыми П. ц. и устойчивыми состояниями равновесия исчерпыва­ются все возможные объекты, к-рые притягивают соседние траектории на фазовой плоскости.




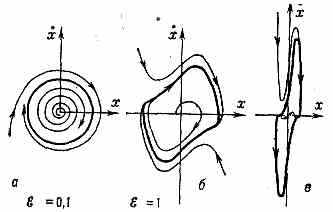
Фазовые портреты генератора Ван дер Поля при разл. значениях нелинейности: а — квазигармонич. колебания; б — сильно неси­нусоидальные; в — релаксационные (ξ=10).


В многомерных динамич. системах с размерностью фазового пространства n3 возможны более сложные притягивающие объ­екты.

• Андронов А. А., В и т т А. А., X а й к и н С. Э., Теория колебаний, 2 изд., М., 1959; Баутин Н. Н., Л е о н т о в и ч Е. А., Методы и приемы качественного исследования динамических систем на плос­кости, М., 1976; Рабинович М. И., Стохастические автоколебания и турбулент­ность, «УФН», 1978, т. 125, в. 1, с. 123.

М. И. Рабинович.

ПРЕЛОМЛЕНИЕ ВОЛН (рефракция волн), изменение направления рас­пространения волны в неоднородной среде, обусловленное зависимостью фазовой скорости волны от координат. П. в. может рассматриваться как от­дельное (независимое от дифракции волн) явление только в рамках при­менимости лучевого описания волно­вых процессов (см. Геометрическая оптика, Геометрическая акустика). Соответственно различают: П. в. на плоской или плавно изогнутой (в мас­штабе длин волн) границе раздела однородных сред и П. в. в плавно не­однородной (в масштабе длины волны) среде (иногда термин «рефракция» от­носят только к этому случаю).

При преломлении плоской монохроматич. волны на плоской границе раздела двух однородные непоглоща­ющих сред направления распростра­нения падающей и преломлённой волн связаны соотношением: sin ₂/sin₁=v₂/v₁ (Снелля закон преломления), где ₁, ₂— углы падения и преломле­ния, т. е. углы между фазовыми ско­ростями v₁, v₂ и нормалью к границе. В изотропных средах величина n₂₁=v₁/v₂ не зависит от угла падения и наз. относит. показателем преломле­ния двух сред; для эл.-магн. волн вво­дят абс. показатель преломления, как отношение скорости света в вакууме к фазовой скорости в среде. При (v₂/v₁)sin₁>1 не существует действит. углов ₂, удовлетворяющих закону П. в., и преломлённая волна отсут­ствует — явление полного внутреннего отражения. Однако и в этом случае закон П. в. формально выполняется при комплексных значениях угла пре­ломления, к-рым соответствуют бегу­щие вдоль границы и экспоненциально спадающие при удалении от неё моды (см. Поверхностные акустические вол­ны). На границе раздела анизотроп­ных сред, в к-рых величина фазовой скорости зависит от направления рас­пространения, v_i=v_i(_i), одной пада­ющей могут соответствовать неск. пре­ломлённых волн, групповые скорости к-рых направлены от границы в глубь среды (угол преломления при этом может быть тупым). П. в. на резких границах раздела сред сопровождается (за редким исключением) отражением волн. Соотношение амплитуд падаю­щей, преломлённой я отражённых волн зависит от природы и поляризации волн и определяется Френеля формулами. На эффекте П. в. основан принцип действия большинства оптич. устройств (микроскопов, телескопов, спектрографов, фотоаппаратов, свето­водов и др.). Рефракцией объясня­ются мн. явления природы: миражи, звуковые каналы в океане и атмосфере, сверхдальняя радиосвязь и др.

• Ф е й н м а н Р., Лейтон Р., С э н д с М., Фейнмановские лекции по фи­зике, 3 изд., т. 3— Излучение. Волны. Кванты, М., 1976; 2 изд., т. 7— Физика сплошных сред, М., 1977; Бреховских Л. М., Волны в слоистых средах, 2 изд., М., 1973.

М. А. Миллер, Г. В. Пермитин.

ПРЕЛОМЛЕНИЕ СВЕТА, изменение направления распространения оптиче­ского излучения (с в е т а) при его про­хождении через границу раздела двух сред. На протяжённой плоской гра­нице раздела однородных изотропных прозрачных (непоглощающих) сред с преломления показателями n₁ и n₂ П. С. определяется след. двумя закономер­ностями: преломлённый луч лежит в плоскости, проходящей через падаю­щий луч и нормаль (перпендикуляр) к поверхности раздела; углы падения  и преломления  (рис.) связаны



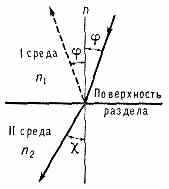
Ход лучей света при преломлении на пло­ской поверхности, разделяющей две про­зрачные среды. Пун­ктиром обозначен от­ражённый луч. Угол преломления % боль­ше угла падения ; это указывает, что в данном случае происходит преломление из оптически бо­лее плотной первой среды в оптически ме­нее плотную вторую (n₁>n₂). n — нормаль к поверхности раздела.


Снелля законом преломления: n₁sin=n₂sin. П. с. сопровождается и отражением света; при этом сумма энергий преломлённого и отражённо­го пучков лучей (количеств. выраже­ния для них следуют из Френеля формул) равна энергии падающего пучка. Их относит. интенсивности за­висят от угла падения, значений n₁ и n₂ и поляризации света в падающем пучке. При н о р м а л ь н о м п а д е н и и отношение ср. энергий пре­ломлённой и упавшей световых волн равно 4n₁n₂/(n₁+n₂)²; в существенном частном случае прохождения света из воздуха (n₁ с большой точностью=1) в стекло с n₂=1,5 оно составляет 96%. Если n₂1 и угол падения arcsin(n₂/n₁), П. с. не происходит и вся энергия, принесённая на грани­цу раздела падающей световой волной, уносится отражённой волной (явление полного внутреннего отражения). При любых , кроме =0, П. с. сопро­вождается изменением состояния по­ляризации света [наиболее сильным при т. н. угле Брюстера =arctg(n₂/n₁), см. Брюстера закон],

583


что используют для получения линей­но-поляризованного света (см. также Стопа в оптике). Зависимость П. с. от поляризации падающих лучей нагляд­но проявляется при двойном лучепре­ломлении в оптически анизотропных средах. В поглощающих средах П. с. можно строго описать, формально ис­пользуя те же выражения, что и для непоглощающих сред, но рассматри­вая n как комплексную вели­чину (мнимая часть к-рой характери­зует поглощение света средой; см., напр., Металлооптика).  при этом становится также комплексным и те­ряет простой смысл угла преломления, какой он имеет для непоглощающих сред. В общем случае n среды зависит от длины волны  света (дисперсия света); поэтому при преломлении немонохроматич. света составляющие его лучи с разл.  идут по разным направ­лениям. На законах П. с. основано устройство линз и мн. оптич. приборов, служащих для изменения направле­ния световых лучей и получения изоб­ражений оптических.

• Ландсберг Г.С., Оптика, 5 изд., ., 1976 (Общий куре физики); Б о р н М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973.

Н. А. Войшвилло.

ПРЕЛОМЛЕНИЯ ПОКАЗАТЕЛЬ от­носительный двух сред n₂₁, безразмер­ное отношение скоростей распростра­нения оптического излучения (с в е т а) в первой (c₁) и во второй (с₂) средах: n₂₁=с₁/с₂. В то же время относит. П. п. есть отношение синусов у г л а п а д е н и я  и у г л а

п р е л о м л е н и я  на границе раздела этих сред: n₂₁=sin/sin (см. Преломле­ние света). Если первой средой слу­жит вакуум (в к-ром скорость света c₀3•10¹⁰ см/с), то П. п. относительно него наз. абсолютным: n=с₀/с. Относит. П. п. есть отношение абс. П. п. сред: n₂₁^:=n₂/n₁.

П. п. зависит от длины волны  (частоты ) излучения (см. Дисперсия света). С диэлектрической проницае­мостью и магнитной проницаемостью среды _ и _, зависящими от , абс.

П. п. связан выражением n_=__. Абс. П. п. среды определяется поляри­зуемостью составляющих её ч-ц (см. Клаузиуса — Моссотти формула, Ло­ренц — Лоренца формула, Рефрак­ция молекулярная), а также струк­турой среды и её агрегатным состоя­нием. Для сред, обладающих опти­ческой анизотропией (естественной или индуцированной), П. п. зависит от направления распространения из­лучения и состояния его поляризации (см. Поляризация света). Типичными анизотропными средами являются мн. кристаллы (см. Кристаллооптика). Среды, поглощающие излучение, опи­сывают комплексным П. п. n^n(1+i), где член, содержащий только n, соответствует направленно­му пропускания, а и = k/4 характеризует поглощение (k — поглощения показатель среды; см. также Ме­таллооптика, Поглощение света).

ПРЕОБРАЗОВАТЕЛИ ИЗМЕРИТЕЛЬ­НЫЕ первичные (датчики), сред­ства измерений, преобразующие изме­ряемую неэлектрич. величину в др. физ. величину, удобную для передачи на расстояние информации об измеряе­мой величине. Выходной величиной П. и. обычно явл. электрич. величина. П. и. входят в измерительные системы и явл. начальным звеном любого изме­рит. канала для измерения неэлектрич. величины.

Обычно выделяют три группы наибо­лее распространённых П. и.: 1) II. и., использующие механич. перемещение для изменения к.-л. параметра элек­трич. цепи или генерирования элек­трич. сигнала. Структурно многие П. и. этой группы состоят из двух частей — чувствит. элемента, пре­образующего измеряемую величину в механич. перемещение, и преобразователя перемещения в электрич. вели­чину; 2) П. и., использующие зави­симость электрич. величины, харак­теризующей чувствит. элемент, от его темп-ры; 3) П. и., использующие из­менение электрич. свойств объекта измерений с изменением его неэлек­трич. параметров.

По виду выходной электрич. вели­чины П. и. делят на п а р а м е т р и ч е с к и е и

г е н е р а т о р н ы е. Выходной величиной параметрич. П. и. явл. пассивный параметр электрич. цепи — сопротивление, ём­кость, индуктивность, взаимная ин­дуктивность. Их применение в изме­рит. системах требует вспомогат. ис­точников питания. Наиболее рас­пространены след. виды параметрич. П. и,: 1) реостатные, к-рые представ­ляют собой чувствит. элемент (щуп, мембрану и др.), перемещающий под воздействием неэлектрич. величины подвижную щётку реостата, изменяя его выходное сопротивление. Исполь­зуются при измерениях с относит. невысокой точностью линейных и уг­ловых перемещений, усилий, давле­ний и др. величин, к-рые могут быть преобразованы в линейное или угло­вое перемещение; 2) тензочувствительные, к-рые основаны на зависи­мости электрич. сопротивления мате­риала проводника от механич. нап­ряжения. Выполняются в виде тонкой (диаметром 0,02—0,05 мм) петлеоб­разно уложенной проволоки, прикле­иваемой на объект измерения или чувствит. элемент П. и. При деформа­циях подложки происходит изменение механич. напряжения проволоки и, соответственно, её электрич. сопро­тивления. Находят широкое приме­нение при измерениях деформаций, механич. напряжений, усилий, массы, давлений, моментов сил и др.; 3) тер­мочувствительные, в к-рых использу­ется зависимость сопротивления про­водника (или полупроводника) от его темп-ры. Применяются для измерения темп-ры, скорости потоков, плотно­сти, состава, теплопроводности газооб­разных и жидких веществ, а также вакуума; просты по конструкции, об­ладают относит. высокой точностью и чувствительностью; 4) индуктивные преобразователи, основанные на за­висимости индуктивности или взаим­ной индуктивности обмоток П. и. от положения отд. элементов магнитопровода, на к-рых они расположены и перемещение к-рых определяется чувствит. элементом, воспринимаю­щим измеряемую величину. Использу­ются при измерениях механич. пере­мещений, давлений, усилий, моментов, расходов и др. величин, преобразуе­мых в механич. перемещение; 5) ём­костные П. и., основанные на зави­симости ёмкости конденсатора от раз­меров и взаимного расположения его обкладок, а также от диэлектрич. проницаемости среды между ними; П. и. с изменением геом. размеров применяют для измерения перемеще­ний и величин, к-рые могут быть пре­образованы в перемещения. Ёмкост­ные П. и. на основе зависимости ём­кости от диэлектрич. проницаемости среды используются при измерениях уровня жидкостей, влажности в-в, толщины материалов из диэлектрика; обладают высокой чувствительностью, относит. малой инерционностью; 6) электролитические, основанные на зависимости электрич. сопротивления электролита от его концентрации, что и определяет их осн. назначение; вы­полняются в виде сосудов с электрода­ми, питание обычно на перем. токе повышенной частоты для исключения электролиза; 7) ионизационные, ос­нованные на зависимости сопротивле­ния газового промежутка, подвер­женного ионизующему излучению, от размеров ионизируемого слоя, св-в газа и интенсивности ионизующего излучения. Представляют собой ио­низац. камеру с источником излуче­ния и электродами. Применяются для измерения величин, преобразуе­мых в механич. перемещение (напр., ионизац. манометр) и для измерений плотности и состава газов. Применя­ются гл. обр. для измерений в агрес­сивных средах и определения пара­метров сред, находящихся под боль­шим давлением или имеющих высо­кую темп-ру.

Выходной величиной г е н е р а т о р н ы х П. и. явл. активная элек­трич. величина (эдс, ток). К генера­торным П. и. относятся: 1) термоэлек­трические, к-рые основаны на термо­электрическом эффекте (см. Термо­электрические явления) в цепи термопа­ры: при различии темп-р точек соеди­нения двух проводников из разнород­ных материалов, в цепи термопары возникает эдс; применяются гл. обр. для измерений темп-ры в широком диапазоне; 2) индукционные, основан­ные на эл.-магн. индукции: при пере­мещении катушки в поле пост. магни­та в ней возникает эдс; применяют-

584


ся гл. обр. для измерений скоро­сти линейных и угловых перемеще­ний, ускорения, параметров вибрации, расхода; 3) пьезоэлектрические, в к-рых используется прямой пьезо­электрический эффект: под воздей­ствием механич. напряжений на по­верхностях кристаллов кварца, сегнетовой соли и др. возникает электрич. заряд; применяются гл. обр. для изме­рения параметров быстро изменяю­щихся величин — переменных уси­лий, давлений, параметров вибраций; 4) гальванические, основанные на ис­пользовании эдс, возникающей при электрохим. вз-ствии электродов с р-ром (гальванич. эдс зависит от со­става и концентрации р-ра); широко используются в хим., нефт., пищ. лром-сти для измерений концентрации ионов в растворах, газах, пульпе, а также измерений влажности.

• Электрические измерения, под ред. А. В. Фремке и Е. М. Душина, 5 изд., Л., 1980; Электрические измерения неэлектрических величин, 5 изд., Л., 1975; Агейкин Д. И., Костина Е. Н., Кузнецова Н. Н., Датчики контроля и регулирования, 2 изд., М., 1965.

В. П. Кузнецов.

ПРЕЦЕССИЯ (от позднелат. praecessio — движение впереди, предшест­вование), движение тв. тела, име­ющего неподвижную точку О, к-рое слагается из вращения с угловой ско­ростью  вокруг оси Oz, неизменно свя­занной с телом, и вра­щения с угловой ско­ростью  вокруг оси Oz₁ (рис.), где

Ox₁,0y_l,0z_l —оси, ус­ловно наз. непод­вижными, по отноше­нию к к-рым рас­сматривается движе­ние тела. ON — прямая, перпендику­лярная к плоскости z₁Oz, наз. линией узлов, =x₁ON— угол П. (см. Эйлеровы углы). Наряду с П. тело совершает также нутационное движение, при к-ром происходит изменение угла ну­тации =z_lOz (см. Нутация).



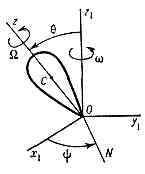
Если во всё время движения =const (нутация отсутствует) и ве­личины ,  также остаются посто­янными, то движение тела наз. р е г у л я р н о й П. Ось 0z описывает при этом вокруг оси П. Oz₁ прямой круговой конус. Такую П. при про­извольных начальных условиях со­вершает закреплённое в центре тяже­сти симметричное тело (гироскоп), на к-рое никакие силы, создающие мо­мент относительно закреплённой точ­ки, не действуют; осью П. в этом слу­чае явл. неизменное направление кине­тич. момента тела (см. Момент коли­чества движения). Симметричное те­ло, закреплённое в произвольной точ­ке его оси симметрии и находящееся под действием силы тяжести (тяжё­лый гироскоп или волчок), совершает при произвольных начальных усло­виях П. вокруг вертикальной оси, сопровождающуюся нутационными ко­лебаниями, амплитуда и период к-рых тем меньше, а частота тем больше, чем больше угловая скорость собств. вращения . Когда >>, видимое движение гироскопа мало отличается от регулярной П.; такую П. наз. псевдорегулярной П. Уг­ловая скорость псевдорегулярной П. тяжёлого гироскопа приближённо оп­ределяется равенством =Pa/I, где Р — вес гироскопа, а — расстояние от неподвижной точки до центра тя­жести, I — момент инерции гироскопа относительно оси симметрии.

С. М. Тарг.