П падение тела

Вид материала

Документы

Содержание Порядковый номер Последействие магнитное Поступательное движение Потенциал зажигания Потенциалы термодинамиче­ские Потенциалы электромагнит­ного поля Максвелла уравнения Гамиль­тона функция (Н) Потенциальная сила Потенциальная энергия Потенциальная яма Рис. 1. Схематич. изо­бражение потенц. ямы U(x). Полная энергия ξ ч-цы — сохраняющаяся ве­личина и поэтому из­ображена на график Рис. 2. Шарик массы m с энергией ξ Потенциальное течение Потенциальный барьер Г (ток через гальванометр должен отсутствовать). Напряжение U В. П. Кузнецов.

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПОРЯДКОВЫЙ НОМЕР элемента, то же, что атомный номер.

ПОРЯДОК ИНТЕРФЕРЕНЦИИ, ве­личина, равная разности хода интер­ферирующих лучей, выраженной в длинах световых волн (см. Интерфе­ренция света). Если интерферирую­щие пучки отражаются от к.-л. по­верхности и при этом происходит изменение фазы, то в П. и. входит алгебр. сумма происходящих при этом скач­ков фаз, выраженная в единицах длин волн (см. Отражение света). Целые и полуцелые значения П. и. соответст­вуют максимумам и минимумам ин­терференционной картины. В реаль­ных устройствах, предназначенных для наблюдения интерференции, П. и. меняется от единиц (Френеля зеркала, Ньютона кольца, двухлучевые интер­ферометры) до 10⁶ и более (эталон Фабри — Перо). Чем выше П. и., тем более монохроматичным должен быть свет для наблюдения интерференц.

картины.

А. П. Гагарин.

ПОСЛЕДЕЙСТВИЕ МАГНИТНОЕ, то же, что магнитная вязкость.

ПОСТОЯННЫЙ ТОК, электрический ток, не изменяющийся с течением вре­мени ни по силе, ни по направлению. П. т. возникает под действием пост. напряжения и может существовать лишь в замкнутой цепи; во всех сече­ниях неразветвлёнпой цепи сила П. т. одинакова (или слабо меняется). Осн. законы П. т.: Ома закон, устанавли­вающий зависимость силы тока от на­пряжения, и Джоуля — Ленца закон, определяющий кол-во теплоты, выде­ляемой током в проводнике. Расчёт разветвлённых цепей П. т. произво­дится с помощью Кирхгофа правил. Источником П. т. явл. электрома­шинные генераторы, а также гальванич. элементы, термоэлементы, фото­элементы, к-рые могут быть сгруппи­рованы в батареи (в т. ч. солнечные батареи). П. т. можно получать вы­прямлением перем. тока с помощью полупроводниковых и др. выпрямите­лей. Источниками П. т. с высоким кпд явл. магнитогидродинамич. генерато­ры. Вторичными, предварительно за­ряжаемыми источниками П. т. служат аккумуляторы.

• Поливанов К. М., Линейные элект­рические цепи с сосредоточенными постоян­ными, М., 1972 (Теоретические основы элект­ротехники, т. 1); К а с а т к и н А. С.. Элек­тротехника, 3 изд., М., 1973.

А. С. Касаткин.

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ, движение тв. тела, при к-ром прямая, соединяющая две любые точки тела, перемещается, оставаясь параллель­ной своему начальному направлению. При П. д. все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по численной величине и направлению скорости и ускорения. Поэтому изуче­ние П. д. тела сводится к задаче кине­матики точки (см. Кинематика).

ПОТЕНЦИАЛ (потенциальная функ­ция) (от лат. potentia — сила), хар-ка векторных полей, к к-рым относятся мн. силовые поля (эл.-магн., гравита­ционное), а также поле скоростей в жидкости и т. п. Если П. векторного поля а(r) — скалярная ф-ция (r), такая, что a=grad, то поле а, наз. потенциальным (иногда П. наз. ф-цию

579


U=-). П.  определяется с точ­ностью до пост. слагаемого. Потенци­альное поле № удовлетворяет Пуассона уравнению, для него выполняется ус­ловие rota=0. Если для поля а мож­но ввести в е к т о р н ы й п о т е н ц и а л А(r), такой, что a=rotA, поле а наз. соленоидальным. Для такого поля выполняется условие divа=0, А(r) в этом случае определя­ется с точностью до градиента от про­извольной ф-ции (калибровочная, или градиентная инвариантность; см. По­тенциалы электромагнитного поля). В общем случае векторное поле можно представить в виде суммы потенциаль­ного и соленоидального полей. Поня­тие П. существенно для описания вз-ствия ч-цы с полем и отыскания полей по заданным распределениям их источников.

ПОТЕНЦИАЛ ЗАЖИГАНИЯ, см. Зажигания потенциал.

ПОТЕНЦИАЛ ЗАПАЗДЫВАЮЩИЙ, см. Запаздывающие потенциалы.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕ­СКИЙ, скалярная энергетич. харак­теристика электростатич. поля; равен отношению потенциальной энергии вз-ствия заряда с полем к величине этого заряда. Напряжённость электро­статич. поля .E и потенциал  связаны соотношением: Е=-grad. П. э. удо­влетворяет Пуассона уравнению. Непосредств. физ. смысл имеет не сам по­тенциал, определяемый подобно потенц. энергии с точностью до произ­вольной постоянной, а разность по­тенциалов.

ПОТЕНЦИАЛЫ ТЕРМОДИНАМИЧЕ­СКИЕ, определённые функции объёма {V), давления (р), темп-ры (Т), энтро­пии (S), числа ч-ц системы (N) и др. макроскопич. параметров (x_i), харак­теризующих состояние термодинами­ческой системы. К П. т. относятся: внутренняя энергия U=U(S, V, N, x_i), энтальпия H=H(S, p, N, x_i), Гельмгольца энергия (свободная энергия, или изохорно-изотермич. потенциал, обо­значается А или F) F=F(V, T,N,x_i), Гиббса энергия (изобарно-изотермич. потенциал, обозначается Ф или G) G=G(p, Т, N, x_i) и др. Зная П. т. как ф-цию указанных параметров, можно получить дифференцированием П. т. все остальные параметры, ха­рактеризующие систему, подобно тому как в механике можно определить компоненты действующих на систему сил, дифференцируя потенц. энергию системы по соответствующим коорди­натам. П. т. связаны друг с другом след. соотношениями:

F=U-TS, H=U+pV, G=F+pV. Если известен к.-л. один из П. т., то можно определить все термодинамич. св-ва системы, в частности получить уравнение состояния. При помощи П. т. выражаются условия термодина­мич. равновесия системы и критерии его устойчивости.

Совершаемая термодинамич. систе­мой в к.-л. процессе работа определя­ется убылью П. т., отвечающего ус­ловиям процесса. Так, при постоянст­ве числа ч-ц (N=const) в условиях теплоизоляции (адиабатический про­цесс, S=const) элементарная работа dA равна убыли внутр. энергии: dA =-dU. При изотермическом процессе (T=const) dA =-dF (в этом процессе работа совершается не только за счёт внутр. энергии, но и за счёт поступаю­щей в систему теплоты). Для систем, в к-рых возможен обмен в-вом с окру­жающей средой (изменение N), воз­можны процессы при пост. р и Т. В этом случае элементарная работа dA' всех термодинамич. сил, кроме сил давления, равна убыли термоди­намич. потенциала Гиббса (G), т. е. dA' =-dG. Теоретич. определение П. т. как ф-ций соответствующих пе­ременных составляет осн. задачу статистич. термодинамики (см. Стати­стическая физика). П. т. широко при­меняются для получения общих соот­ношений между физ. св-вами мак­роскопич. тел и анализа термодина­мич. процессов и условий равновесия в физ.-хим. системах. Термин «П. т.» ввёл франц. физико-химик П. Дюгем (1884), основатель же метода П. т. амер. физик Дж. У. Гиббс пользовал­ся термином «фундаментальные функ­ции».

• Ландау Л. Д., Лифшиц Е. М., Статистическая физика, 2 изд., М., 1964 (Теоретическая физика, т. 5); Л е о н т о в и ч М. А., Введение в термодинамику, 2 изд., М.—Л., 1952; Рейф Ф., Статистичес­кая физика, пер. с англ., М., 1972 (Берклеевский курс физики, т. 5); Г и б б с Д. В., Термодинамические работы, пер. с англ., М.—Л., 1950.

Г. Я. Мякишев.

ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТ­НОГО ПОЛЯ, энергетич. характери­стики эл.-магн. поля, к-рые вводят для описания поля наряду с силовыми хар-ками — напряжённостью элек­трич. поля Е и магн. индукцией В. В электростатике векторное элект­рич. поле можно характеризовать од­ной скалярной ф-цией — потенциа­лом электростатическим. В общем случае для описания произвольного эл.-магн. поля вместо Е и В можно ввести две др. величины: векторный потенциал А (х, у, z, t) и скалярный потенциал (x, у, z, t), где х, у, z — координаты, t — время, при этом В и E однозначно выражаются через А и :



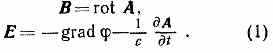
Ур-ния для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения, что упрощает задачу нахождения переменных эл.-магн. полей. Существ. упрощение ур-ний для П. э. п. возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и  выбрать новые потенциалы



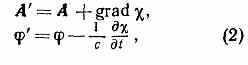
где  — произвольная ф-ция коорди­нат и времени, то векторы В и Е, опре­деляемые ур-ниями (1), не изменятся. Инвариантность эл.-магн. поля по от­ношению к преобразованиям потен­циалов (2) носит назв. к а л и б р о в о ч н о й, или г р а д и е н т н о й, и н в а р и а н т н о с т и. Калибро­вочная инвариантность позволяет на­ложить на П. э. п. дополнит. условие. Обычно таким дополнит. условием явл. условие Лоренца:



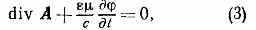
где  и  — диэлектрич. и магн. про­ницаемости среды. При использовании условия (3) ур-ния для П. э. п. в од­нородной среде (=const, =const), получаемые из ур-ний Максвелла, приобретают одинаковую форму:



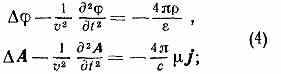
здесь =д²/дx²+д²/дy²+д²/дz²— т. н. оператор Лапласа,  и j — плотности за­ряда и тока, a v=c/ — скорость распространения эл.-магн. поля в среде. Если =0 и j=0, то П. э. п. удовлетворяют волновому уравнению.

Ур-ния (4) позволяют определить потенциалы A и  по известному рас­пределению зарядов и токов, а следо­вательно, с помощью формул (1) — и хар-ки эл.-магн. поля В и Е. Частные решения ур-ний (4), удовлетворяющие причинности принципу, наз. з а п а з д ы в а ю щ и м и п о т е н ц и а л а м и. Запаздывающие потенциалы в точке с координатами х, у, z в момент времени t определяются плотностя­ми заряда и тока в точке с координа­тами х', у', z' в предшествующий момент времени =t-R/v, где R=((х-х')²+(у-у')²+(z-z')²)— расстояние от источника поля до точки наблюдения.

Если заряды и токи распределены в конечной области пространства G, то запаздывающие потенциалы опреде­ляются интегрированием элементар­ных потенциалов от зарядов и токов, сосредоточенных в бесконечно малых объёмах dx'dy'dz', с учётом времени запаздывания:



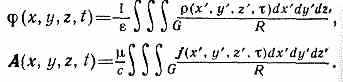
Через П. э. п, выражается Гамиль­тона функция (Н) заряженной ч-цы, движущейся в эл.-магн. поле:



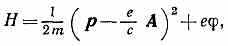
где р — импульс ч-цы, е и m — её заряд и масса. Соответственно через П. э. п. выражается оператор Гамиль­тона (гамильтониан) в квант. теории.

• См. лит. при ст. Максвелла уравнения.

Г. Я. Мякишев.

580


ПОТЕНЦИАЛЬНАЯ СИЛА, сила, ра­бота к-рой зависит только от началь­ного и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки (см. Силовое поле).

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ, часть общей механич. энергии системы, за­висящая от взаимного расположения материальных точек, составляющих эту систему, и от их положений во внеш. силовом поле (напр., гравита­ционном; см. Поля физические). Чис­ленно П. э. системы в данном её по­ложении равна работе, к-рую произве­дут действующие на систему силы при перемещении системы из этого поло­жения в то, где П. э. условно прини­мается равной нулю (П=0). Из опре­деления следует, что понятие «П. э.» имеет место только для консервативных систем, т. е. систем, у к-рых работа действующих сил зависит только от начального и конечного положения системы. Так, для груза весом Р, под­нятого на высоту h, П. э. будет равна П=Ph (П=0 при h=0); для груза, прикреплённого к пружине, П=0,5kl², где l — удлинение (сжа­тие) пружины, k — её коэфф. жёст­кости (П=0 при l=0); для двух ч-ц с массами m_t и m₂, притягивающимися по закону всемирного тяготения, П=fm₁m₂/r, где f — гравитац. по­стоянная, r — расстояние между ч-ца­ми (П=0 при r=); аналогично опре­деляется П. э. для двух точечных электрич. зарядов е₁ и е₂.

Иногда термин «П. э.» употребляют, подразумевая любую энергию, содер­жащуюся в системе в скрытом виде.

С. М. Тарг.

ПОТЕНЦИАЛЬНАЯ ЯМА, ограни­ченная область пространства, опреде­ляемая физ. природой вз-ствия ч-ц, в к-рой потенц. энергия ч-цы меньше, чем вне её. Термин «П. я.» происходит от вида графика, изображающего за­висимость потенц. энергии U ч-цы в силовом поле от её положения в пр-ве (в случае одномерного движения — от координаты х; рис. 1). Такая форма ависимости U(х) возникает в поле сил притяжения.



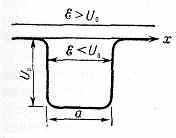
Рис. 1. Схематич. изо­бражение потенц. ямы U(x). Полная энергия ξ ч-цы — сохраняющаяся ве­личина и поэтому из­ображена на графике горизонтальной ли­нией.


Хар-ки П. я.— ши­рина а (расстояние, на к-ром прояв­ляется действие сил притяжения) и глубина U₀ (равная разности потенц. энергий частицы на «краю» ямы и на её «дне», соответствующем миним. по­тенц. энергии, к-рую удобно положить равной нулю). Осн. св-во П. я.— способность удерживать ч-цу, полная энергия ξ к-рой меньше U₀; такая ч-ца внутри П. я. будет находиться в связанном состоянии.

В классической меха­нике ч-ца с энергией ξ0 не сможет вылететь из П. я. и будет всё время двигаться в огранич. области пр-ва внутри ямы; положение ч-цы на «дне» ямы отвечает устойчивому рав­новесию и соответствует нулевой ки­нетич. энергии ч-цы. Если ξ>U₀, то ч-ца преодолевает действие сил при­тяжения и свободно покидает яму. Пример — движение упругого шари­ка, находящегося в поле сил земного притяжения, в обычной яме с жёстки­ми пологими стенками (рис. 2).



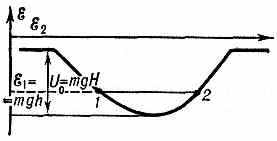
Рис. 2. Шарик массы m с энергией ξ₁₀ не может покинуть яму глубиной U₀=mgH (где g — ускорение свободного падения, H— высота обычной ямы, в к-рую попал шарик) и будет совершать колебания между точка­ми 1 и 2 (если пренебречь трением), подни­маясь лишь до высоты h=ξ₁/mg. Если энер­гия шарика ξ₂>U₀. то он покинет яму и уйдёт на бесконечность с пост. скоростью v, определяемой из соотношения mv²/2=ξ₂-U₀.


В квантовой механике, в отличие от классической, энергия ч-цы, находя­щейся в связанном состоянии в П. я., может принимать лишь определённые дискр. значения, т. е. существуют дискр. уровни энергии. Однако такая дискретность уровней становится за­метной лишь для систем, имеющих микроскопич. размеры и массы. По порядку величины расстояние ξ между уровнями для ч-цы массы т в «глубокой» яме ширины а опреде­ляется величиной ξ~ћ²/ma². Наи­низший (основной) уровень энергии лежит выше «дна» П. я. (см. Нулевая энергия). В П. я. малой глубины (U₀ћ²/ma²) связанное состояние мо­жет вообще отсутствовать (так, про­тон и нейтрон с антипараллельными спинами не образуют связанной сис­темы, несмотря на существование сил притяжения между ними).

Кроме того, согласно квант. меха­нике, ч-ца, находящаяся в П. я. со «стенками» конечной толщины (типа кратера вулкана), может покинуть П. я. за счёт туннельного эффекта даже в том случае, если её энергия меньше U₀.

Форма П. я. и её размеры опреде­ляются физ. природой вз-ствия ч-ц. Важный случай — кулоновская П. я., описывающая притяжение ат. эл-на ядром. Понятие «П. я.» широко при­меняется в ат. и мол. физике, в физике тв. тела и ат. ядра.

• См. лит. при статьях Квантовая меха­ника, Твёрдое тело, Ядро атомное.

ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ, без­вихревое течение жидкости, при к-ром каждый малый объём деформируется и перемещается поступательно, но не имеет вращения (вихря). П. т. может иметь место при определённых усло­виях только для идеальной (лишённой

трения) жидкости, напр. когда дви­жение начинается из состояния покоя, когда жидкость несжимаема и в ней начинает двигаться погружённое тело или происходит удар тела о поверх­ность жидкости и т. п. У реальных жидкостей и газов П. т. происходит в тех областях, где силы вязкости нич­тожно малы по сравнению с силами давления и нет завихрений. Изучение П. т. существенно упрощается тем, что сводится к отысканию только од­ной функции координат и времени, наз. потенциальной функцией. ПОТЕНЦИАЛЬНЫЙ БАРЬЕР, огра­ниченная в пространстве область вы­сокой потенц. энергии ч-цы в силовом поле, по обе стороны к-рой потенц. энергия б. или м. резко спадает. П. б. соответствует силам отталкивания.



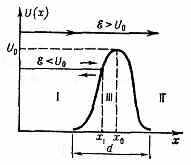
На рис. изображён П. б. простой формы для случая одномерного (по оси х) движения ч-цы. В нек-рой точке x=x₀ потенц. энергия U(х) принимает макс. значение U₀, наз. высотой барь­ера. П. б. делит пр-во на две области (I и II), в к-рых потенц. энергия ч-цы меньше, чем внутри П. б. (в области III; d — ширина барьера).

В к л а с с и ч е с к о й м е х а н и к е прохождение ч-цы через П. б. возможно лишь в том случае, если её полная (кинетическая + потенциаль­ная) энергия ξ не меньше высоты П. б.,ξU₀; тогда ч-ца пролетает над барьером. Если же энергия ч-цы недо­статочна для преодоления барьера, ξ<U₀, то в нек-рой точке х₁ ч-ца, дви­жущаяся слева направо, останавли­вается и затем движется в обратном направлении. То есть П. б. явл. как бы непрозрачной стенкой, барьером, для ч-ц с энергией, меньшей высоты П. б.,— отсюда назв. «П. б.».

В к в а н т о в о й м е х а н и к е, в отличие от классической, возможно прохождение через П. б. ч-ц с энергией ξ₀ (это явление наз. туннельным эффектом) и отражение от П. б. ч-ц с ξ>U₀ (надбарьерное отражение). Такие особенности поведения ч-ц в квант. физике связаны с корпускулярно-волновой природой микрочастиц (см. Квантовая механика). Туннель­ный эффект существен лишь для сис­тем, имеющих микроскопич. размеры и массы. Чем уже П. б. и чем меньше разность U₀-ξ, тем больше вероят­ность для частицы пройти через барьер.

ПОТЕНЦИОМЕТР (от лат. potentia — сила и греч. metreo — измеряю), при-

581


бор для измерения компенсац. методом эдс и напряжения, а также величин, функционально с ними связанных.

П. пост. и перем. тока существенно различаются. В П. пост. тока (рис.) измеряемая эдс Е_х уравновешивается (компенсируется) известным регули­руемым напряжением U_к. О моменте



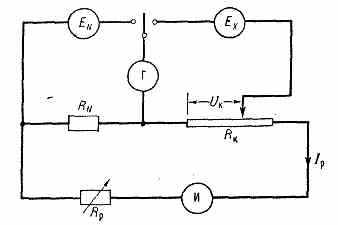
Принципиальная схема потенциометра пост. тока: Е_N и Е_х— известная и измеряемая эдс; 1р — рабочий ток; U_к — известное регули­руемое напряжение; И — измерит. прибор (амперметр).


равновесия судят по показаниям галь­ванометра Г (ток через гальванометр должен отсутствовать). Напряжение U_к получают как падение напряжения на известной части сопротивления R_к от рабочего тока I_р. Значение I_р уста­навливается при помощи регулируе­мого сопротивления R_р по данным сравнения падения напряжения на сопротивлении R_N с эдс E_N меры, в качестве к-рой обычно применяют нормальный элемент. Выпускаются высокоомные и низкоомные П. (сопро­тивление цепи рабочего тока, соответ­ственно, ~ 10000 Ом и ~10 Ом). Последние применяются для измере­ний относит. малых эдс и эдс источни­ков с малым внутр. сопротивлением. П. пост. тока измеряют эдс от 0,02 мкВ до 2 В с осн. относит. погрешностью до 0,0005%.

Для измерений неэлектрич. величин, преобразованных в эдс пост. тока, широко пользуются автоматич. П., в к-рых вместо гальванометра включён усилитель. Усиленное нескомпенси­рованное напряжение управляет ре­версивным двигателем, перемещающим ползунок сопротивления R_к до момен­та компенсации измеряемой эдс. Наи­большее распространение получили автоматич. П. для измерений темп-ры в комплекте с термопарами. Осн. по­грешность таких П. в % от диапазона измерений до 0,25%.

В П. перем. тока компенсирующее напряжение должно совпадать по ам­плитуде, частоте и фазе с гармониче­ски изменяющейся измеряемой эдс. При этом П. перем. тока позволяют измерять эдс как векторную величину (по амплитуде и фазе). В качестве ну­левого индикатора обычно используют вибрац. гальванометр. По точности П. перем. тока существенно уступают П.

пост. тока из-за того, что для перем. тока нет мер, аналогичных нормаль­ному элементу. П. перем. тока имеют верх. предел измерений до 2 В, в ком­плекте с делителем напряжения — до 300 В, осн. относит. погрешность до 0,1%, частотный диапазон от 50 Гц до 10 кГц.

Требования к П. стандартизованы в ГОСТ 22261—76 (общие технич. усло­вия), ГОСТ 9245—79 (П. пост. тока), ГОСТ 11921—78 (П. перем. тока) и ГОСТ 7164—78 (П. автоматич. пост. тока).

• Основы электроизмерительной техники, М., 1972; Справочник по электроизмери­тельным приборам, 2 изд., Л., 1977.

В. П. Кузнецов.