П падение тела

Вид материала

Документы

Содержание Многопереходные полупроводниковые приборы Переходом, гетеропереходом или переходом металл — полупроводник Полупроводниковый лазер Рис. 1. Полупроводники, используемые в полупроводниковых лазерах, и спектральные диапазоны их излучения. Некоторые характеристики инжекционных лазеров Рис. 4. Схема гетеролазера с двухсторонней гетероструктурой на основе AlGaAs (a) и его энергетич. диаграмма (б); ξ Рис. 5. Полупроводниковые лазеры с элект­ронной накачкой в отпаянной трубке. Полутеневые приборы Полюс магнитный С. Герштейн. Поляризационная микроско­пия Рис. 1. Схемы: а — пластинки, нагружен­ной в своей плоскости; б — элемента объ­ёма в напряжённом состоянии; а — нормаль­ные напр Р,  — длина волны света лампы S Рис. 2. Схема кругового полярископа(/4— компенсирующие пластинки; Э — экран). Рис. 3. Картина полос при равномерном растягивании пластинки с круглым отвер­стием. В. И. Савченко.

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

Табл. 2. МНОГОПЕРЕХОДНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ



568


Табл. 3. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ С ОДНИМ p-n -ПЕРЕХОДОМ, ГЕТЕРОПЕРЕХОДОМ ИЛИ ПЕРЕХОДОМ МЕТАЛЛ — ПОЛУПРОВОДНИК




ПОЛУПРОВОДНИКОВЫЙ ДЕТЕК­ТОР, прибор для регистрации ч-ц, осн. элементом к-рого явл. кристалл полупроводника. Регистрируемая ч-ца, проникая в кристалл, генерирует в нём дополнит. (неравновесные) элек­тронно-дырочные пары. Носители за­ряда (электроны и дырки) под действи­ем приложенного электрич. поля «рас­сасываются», перемещаясь к электро­дам П. д. В результате во внеш. цепи П. д. возникает электрич. импульс, к-рый далее усиливается и регистри­руется (рис.). Для достижения доста­точно высокой чувствительности необ­ходимо, чтобы в отсутствии регистрируемых ч-ц полупроводник был обед­нён носителями, т. е. имел миним. электропроводность.



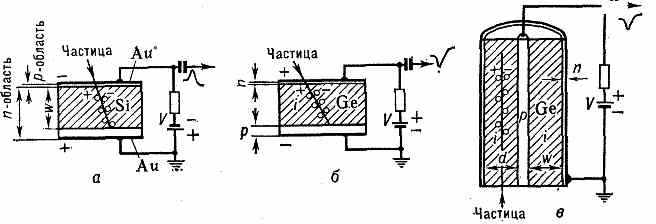
Рис. Полупроводниковые детекторы (штриховкой выделена чувствит. область): n — об­ласть полупроводника с электронной проводимостью; p — с дырочной; г — с собств. проводимостью; а — кремниевый поверхностно-барьерный детектор; б — планарный диффузионно-дрейфовый германиевый детектор; в — коаксиальный диффузионно-дрейфо­вый Ge(Li)-детектор.


Это достигается использованием p — n-перехода, на к-рый подают обратное (запирающее) напряжение V. Слой полупроводника вблизи границы p — n-перехода, обед­нённый носителями заряда и обладаю­щий высоким уд. электросопротивле­нием , явл. чувствит. слоем П. д. Глу­бина чувствит. слоя W=0,5V (W в мкм,  в Ом•см, V в В). Остальная часть кристалла полупроводника об­разует нечувствительный (мёртвый) слой.

Заряд, собранный на электродах П. д., пропорц. энергии, выделенной ч-цей при прохождении через чувст­вит. слой. Поэтому, если ч-ца полностью тормозится в нём, П. д. может работать как спектрометр. Ср. энер­гия, необходимая для образования од­ной электронно-дырочной пары, в по­лупроводнике мала (у Si — 3,8 эВ, у Ge — 2,9 эВ). В сочетании с высокой плотностью в-ва это позволяет полу­чить высокую разрешающую способ­ность по энергии ξ/ξ, достигаю­щую ~1% при ξ~10 кэВ и ~0,1% при ξ~1000 кэВ. Если ч-ца пол­ностью тормозится в чувствит. слое, то эффективность её регистрации ~100%. Большая подвижность носи­телей тока в Ge и Si позволяет быстро собирать заряд на электродах за время ~10^-8 с, что обеспечивает высокое временное разрешение П. д.

Высокое энергетич. разрешение П. д. может быть достигнуто лишь при ох­лаждении детекторов до темп-ры жид­кого азота, т. к. из-за малой ширины запрещённой зоны в Si и Ge даже в случае собств. проводимости концен­трация свободных носителей при ком­натной темп-ре велика. Кроме того, при охлаждении существенно увели­чивается подвижность носителей, бла­годаря чему обеспечивается более пол­ный их сбор на электродах. В связи с этим П. д. обычно размещают в криостатах, в к-рых поддерживается вакуум ~10^-6 мм рт. ст.

В П. д. используются т. н. поверх­ностно-барьерные (сплавные) переходы (W~1 — 2 мм, мёртвый слой ~0,1 — 2 мкм) и диффузионные переходы. Введение примеси Li в Ge и Si (ионы Li захватывают носители и умень­шают проводимость) увеличивает W для плоских (п л а н а р н ы х) П. д. до 15 мм (диффузионно-дрейфовые П. д., имеющие pin-структуру) и поз­воляет создавать коаксиальные дрейфо­вые германиевые П. д. с примесью Li [Ge(Li)] с рабочим объёмом ~200 см³ для регистрации жёстких -квантов (ξ1МэВ). Из «сверхчистого» Ge (концентрация примесей ~10^-10 в 1 см³), сопротивление к-рого близко к собственному, также изготавливают планарные П. д. площадью ок. 19 см² и W16 мм и коаксиальные П. д. объ­ёмом до 75 см³.

Для обеднения носителями в П. д. используется также предварит. облу­чение кристалла -квантами. Образую­щиеся радиационные дефекты явл. ловушками для носителей (радиацион­ные П. д.). Поверхностно-барьерные и диффузионные кремниевые П. д. обладают миним. толщиной мёртвого слоя (от десятых долей мкм до неск. мкм). Их используют для спектромет­рии осколков деления атомных ядер, -частиц с энергиями 20 МэВ, про­тонов с энергиями 5 МэВ и электро­нов с энергиями 200 кэВ. В этом случае пробег ч-ц ещё полностью ук­ладывается в чувствит. слое П. д. Однако П. д. используются также для спектрометрии ч-ц более высоких энер-

569


гий, когда пробег ч-ц больше глубины обеднённой области. При этом с по­мощью П. д. определяют удельные ионизац. потери энергии ч-ц или их координаты с пространств. разрешени­ем до 50 мкм (позиционно-чувствительные П. д.).

Для спектрометрии мягкого рентг. излучения обычно используют диф­фузионно-дрейфовые П. д. из кремния с примесью лития, а также германие­вые П. д. Для спектрометрии -квантов применяют коаксиальные диффу­зионно-дрейфовые П. д. из Ge(Li) и из сверхчистого Ge. Применяют также полупроводники с большой шириной запрещённой зоны ξ_g (CdTe с ξ_g=1,5 эВ и HgI с ξ_g=2,l эВ). Однако из-за большей ср. энергии образова­ния пары электрон — дырка их энер­гетич. разрешение хуже, чем в случае Ge и Si.

В процессе работы в П. д. происхо­дит накопление радиац. дефектов в его чувствит. объёме, в результате чего его спектрометрич. св-ва ухудшаются. Предельные потоки для быстрых ней­тронов 10¹²—10¹³ см^-2, для -частиц 10¹⁰ см^-2, для электронов с энергией 2—5 МэВ 10¹³—10¹⁴ см^-2, для -квантов больше 10⁸ рад.

•Дирнли Дж., Нортроп Д., По­лупроводниковые счетчики ядерных излу­чений, пер. с англ., М., 1966; Прикладная спектрометрия с полупроводниковыми детек­торами, М., 1974.

А. Г. Беда.

ПОЛУПРОВОДНИКОВЫЙ ЛАЗЕР, лазер на основе полупроводникового кристалла. В отличие от лазеров др. типов, в П. л. используются излучательные квант. переходы между раз­решёнными энергетич. зонами, а не дискр. уровнями энергии (см. Полупро­водники). В полупроводниковой ак­тивной среде может достигаться очень большой показатель оптич. усиления (до 10⁴ см^-1), благодаря чему размеры активного элемента П. л. исключи­тельно малы (длина резонатора ~50 мкм — 1 мм). Помимо компакт­ности, особенностями П. л. явл. малая инерционность (~10^-9 с), высокий кпд (до 50%), возможность спектральной перестройки и большой выбор в-в для генерации в широком спектральном диапазоне от =0,3 мкм до 30 мкм (рис. 1). Активными ч-цами в П. л. служат избыточные (неравновесные) эл-ны проводимости и дырки, т. е. свободные носители заряда, к-рые мо­гут инжектироваться, диффундировать и дрейфовать в активной среде. Важ­нейшим способом накачки в П. л. явл. инжекция через p — n-переход или гетеропереход (см. Электронно-дыроч­ный переход), позволяющая осущест­вить непосредств. преобразование электрич. энергии в когерентное из­лучение (инжекционный ла­зер). Др. способами накачки служат электрич. пробой (напр., в т. н. стримерных лазерах), бомбардиров­ка эл-нами (П. л. с э л е к т р о н н о й н а к а ч к о й) и освещение (П. л. с о п т и ч. н а к а ч к о й). П. л. пред­ложены Н. Г. Басовым и др., впер­вые осуществлены на р — n-переходе в кристалле GaAs P. Холлом, М. И. Нейтеном (США) и др., с элект­ронной накачкой Басовым с сотр.



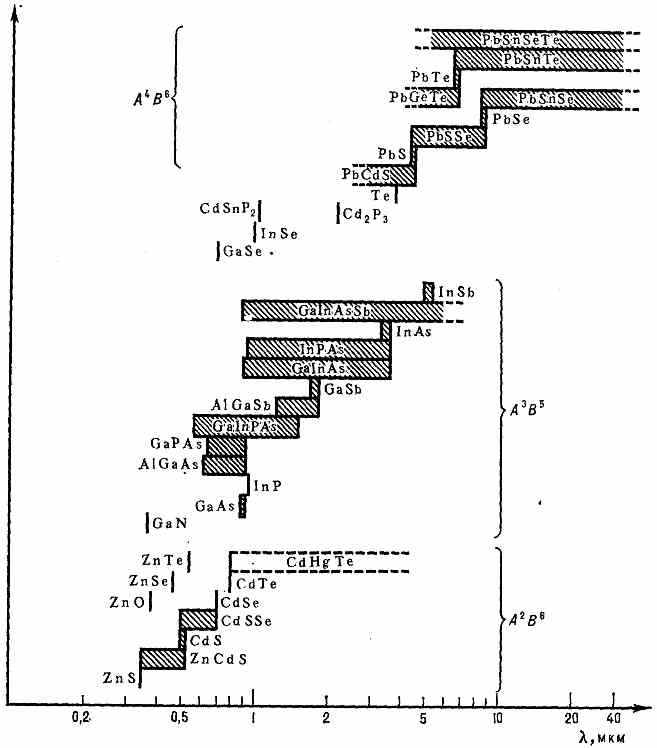
Рис. 1. Полупроводники, используемые в полупроводниковых лазерах, и спектральные диапазоны их излучения.


Оптич. усиление в полупроводниках возникает под действием интенсивной накачки при выполнении условий ин­версии населённости уровней вблизи



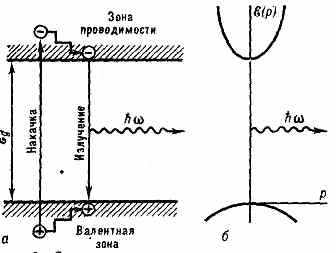
Рис. 2. Схема накачки (а) и зонная диаграм­ма (б) полупроводника, используемого в по­лупроводниковом лазере; ξ — энергия эл-на, р — квазиимпульс, ћ — энергия испус­каемого кванта.


дна ξ_с в зоне проводимости и потолка ξ_v в валентной зоне (рис. 2). При этом вероятность заполнения эл-нами верх­них рабочих уровней в разрешённой зоне (зоне проводимости) больше, чем нижних уровней (валентной зоны). В этом случае вынужденные излучат.

переходы преобладают над поглощат. переходами. Величина оптич. усиле­ния зависит не только от интенсивно­сти накачки, но и от др. факторов: вероятности излучательной рекомби­нации, внутр. квантового выхода из­лучения, темп-ры. В качестве лазер­ных материалов используются прямозонные полупроводники (напр., GaAs, CdS, PbS), в к-рых квант. выход излу­чения может достигать 100%. На непрямозонных полупроводниках (Ge, Si) пока не удаётся создать П. л. Раз­нообразие полупроводниковых лазер­ных материалов позволяет перекрыть широкий спектральный диапазон с по­мощью П. л. (табл. 1, 2).

Инжекционный П. л. представляет собой полупроводниковый диод, две плоскопараллельные грани к-рого, перпендикулярные плоскости p—n-перехода и гетероперехода, служат зер-

570


Табл. 1. НЕКОТОРЫЕ ХАРАКТЕРИСТИКИ ИНЖЕКЦИОННЫХ ЛАЗЕРОВ



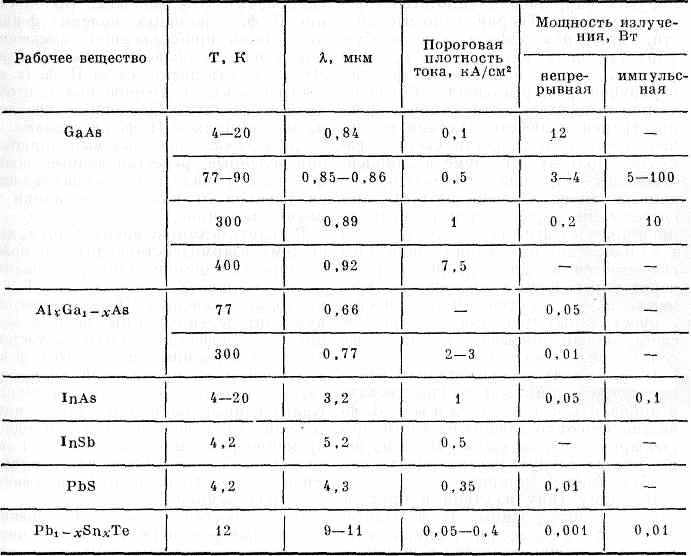
Табл. 2. ПОЛУПРОВОДНИКИ, ИСПОЛЬЗУЕМЫЕ В ГЕТЕРОЛАЗЕРАХ



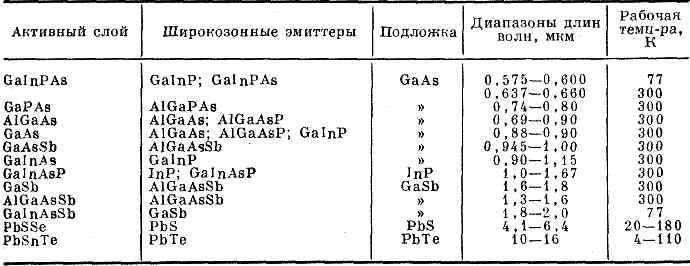
калами оптического резонатора (коэфф. отражения ~30%, рис. 3). Иногда при­меняются внеш. резонаторы. Инверсия заполнения достигается при большом прямом токе через диод за счёт инжекции избыточных носителей в слой, прилегающий к переходу. Генерация






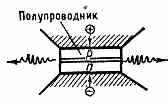
Рис. 3. Вверху инжекционный лазер на р —n-переходе; вни­зу — образцы инжекционных полупровод­никовых лазеров.


когерентного излучения возникает в полосе краевой люминесценции, если оптич. усиление способно превзойти потери энергии, связанные с выводом излучения наружу, поглощением и рассеянием внутри резонатора. Ток, соответствующий началу генерации, наз. пороговым. Плотность порогового тока в инжекционных П. л. обычно ~1 к А/см² (табл. 1).

Наибольшее распространение полу­чили П. л. на основе гетероструктур (гетеролазеры), они имеют наиболее низкие пороговые плот­ности тока при темп-рах 300 К. Гетеролазер содержит 2 гетероперехо­да, один типа p — n, инжектирую­щий эл-ны (эмиттер), и другой, типа p — p, ограничивающий диффузное растекание носителей заряда из ак­тивного слоя; активная область зак­лючена между ними. В т. н. п о л о с к о в ы х л а з е р а х активная область в форме узкой полоски шириной 1— 20 мкм протягивается вдоль оси резонатора от одного зер­кала к другому. Благодаря малым раз­мерам активной области пороговый ток полосковых гетеролазеров доста­точно мал (5—150 мА) для получения непрерывной генерации при T=300 К. Мощность излучения таких П, л. (~100 мВт) ограничена перегревом активной области. В коротких им­пульсах П. л. испускают большую мощность (до 100 Вт), к-рая ограниче­на оптич. разрушением торцевых гра­ней. Многоэлементные инжекционные П. л. создают в импульсе мощность до 10 кВт.

Полупроводники, из к-рых могут быть изготовлены гетеролазеры, при разл. хим. составе должны обладать одинаковым периодом крист. решётки. Используются многокомпонентные тв. растворы, среди к-рых можно найти непрерывные ряды в-в с постоянным периодом решётки (изопериодические системы). Напр., в гетеролазере на основе твёрдых растворов Al_xGa_t-xAs гетероструктуру составляют слои (рис. 4): p(Al_xGa_1-xAs); p(GaAs); n(Al_xGa_1-xAs).



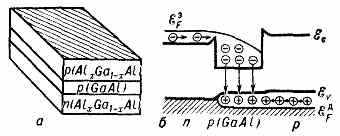
Рис. 4. Схема гетеролазера с двухсторонней гетероструктурой на основе AlGaAs (a) и его энергетич. диаграмма (б); ξ_с и ξ_v — края зоны проводимости и валентной зоны; ξ^э_F и ξ^д_F — энергии Ферми для эл-нов и дырок.


В П. л. с электронной накачкой ис­пользуются пучки быстрых эл-нов с энергией 10⁴—10⁵ эВ (как правило, меньшей порога образования радиа­ционных дефектов в кристалле). Избы­точные носители заряда образуются в результате ионизации при замедлении быстрых эл-нов. Глубина проникнове­ния эл-нов зависит от энергии и может достигать 10^-2 см. П. л. этого типа, помимо активного элемента, содержат источник высокого напряжения, элек­тронную пушку и систему фокусиров­ки и управления пучком. Достоинство



Рис. 5. Полупроводниковые лазеры с элект­ронной накачкой в отпаянной трубке.

571


П. л. с электронной накачкой — воз­можность сканирования излучающего пятна по активному элементу, что поз­воляет осуществить воспроизведение и проектирование на большой экран телевизионного изображения (разно­видность лазерного телевидения). Мощ­ность излучения в импульсе в П. л. этого типа может достигать 1 МВт (при накачке большого объёма кри­сталла или многоэлементной мишени). П. л. с электронной накачкой изготов­ляются в виде отпаянной вакуумной трубки с оптич. окном для вывода лазерного излучения (рис. 5).

• Б а с о в Н. Г., Полупроводниковые квантовые генераторы, «УФН», 1965, т. 85, в. 4; Богданкевич О. В., Дарзнек С. А., Е л и с е е в П. Г., Полупроводнико­вые лазеры, М., 1976; Елисеев П. Г., Полупроводниковые лазеры и преобразова­тели, в кн.: Итоги науки и техники. Сер. Радиотехника, т. 14, ч. 1, М., 1978.

П. Г. Елисеев.

ПОЛУТЕНЕВЫЕ ПРИБОРЫ, назва­ние одного из типов поляриметров, в к-рых измерение угла вращения плоскости поляризации сводится к ви­зуальному уравниванию яркости двух половин поля зрения прибора. Под­робнее см. в ст. Поляриметр.

ПОЛУТЕНЬ, пространство между об­ластями полной тени и полного света, образующееся за непрозрачным телом при освещении его источником света с большими угловыми размерами (рис.).



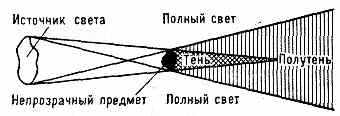
В области П. видна только часть источника (в тени источник не виден совсем).

ПОЛЮС МАГНИТНЫЙ, см. Магнит­ный полюс.

ПОЛЯ ФИЗИЧЕСКИЕ, особая фор­ма материи; физ. система с бесконечно большим числом степеней свободы. Примерами П. ф. могут служить эл.-магн, и гравитац. поля, поле яд. сил, а также волновые (квантованные) по­ля, соответствующие разл. элем. ч-цам.

Понятие поля (электрич. и магн.) было введено англ. учёным М. Фара­деем (30-е гг. 19 в.). Концепция поля явилась возрождением теории близкодействия (см. Взаимодействие), осново­положником к-рой был франц. учёный Р. Декарт (1-я пол. 17 в.). В 60-х гг. 19 в. англ. физик Дж. Максвелл раз­вил идею Фарадея об эл.-магн. поле и сформулировал математически его законы (Максвелла уравнения).

Согласно концепции, поля, участву­ющие во вз-ствии ч-цы, создают в каж­дой точке окружающего их пр-ва осо­бое состояние — поле сил, проявляю­щееся в силовом воздействии на др. ч-цы, помещаемые в к.-л. точку этого пр-ва. Первоначально выдвигалась механистич. интерпретация поля как упругих напряжений гипотетич. сре­ды — «эфира». Теория относительно­сти, отвергнув «эфир» как особую упругую среду, вместе с тем придала фундам. смысл понятию П. ф. как первичной физ. реальности. Согласно теории относительности, скорость рас­пространения любого вз-ствия не мо­жет превышать скорости света в ва­кууме. Поэтому в системе взаимодей­ствующих ч-ц сила, действующая в данный момент времени на к.-л. ч-цу системы, не определяется расположе­нием др. ч-ц в этот же момент времени, т. е. изменение положения одной ч-цы сказывается на др. ч-це не сразу, а через определённый промежуток вре­мени. Т. о., вз-ствие ч-ц, относит. скорость к-рых сравнима со скоростью света, можно описывать только через создаваемые ими поля.

П. ф. не только осуществляют вз-ст­вие между ч-цами; могут существовать и проявляться свободные П. ф. независимо от создавших их ч-ц (напр., электромагнитные волны.). Поэтому яс­но, что их следует рассматривать как особую форму материи.

Каждому типу вз-ствий в природе отвечают определённые П. ф. Описа­ние П. ф. в классич. (неквантовой) теории поля производится с помощью одной или неск. (непрерывных) ф-ций поля, зависящих от координаты точки (х, у, z), в к-рой рассматривается поле, и от времени (t). Так, эл.-магн. поле может быть полностью описано с по­мощью четырёх ф-ций: скалярного потенциала (x, у, z, t) и вектор-по­тенциала А (х, у, z, t), к-рые вместе составляют четырёхмерный вектор в пространстве-времени. Напряжённо­сти электрич. и магн. полей выража­ются через производные этих ф-ций. В общем случае число независимых ф-ций определяется числом внутр. степеней свободы ч-ц, соответствую­щих данному полю (см. ниже), напр. их спином, изотопическим спином и т. д. Исходя из общих принципов — требований релятивистской инвари­антности и нек-рых более частных предположений (напр., для эл.-магн. поля — суперпозиции принципа и гра­диентной инвариантности), можно из ф-ций поля составить выражение для действия и с помощью наименьшего действия принципа получить дифф. ур-ния, определяющие поле. Значения ф-ций поля в каждой отд. точке можно рассматривать как обобщённые коорди­наты П. ф. Следовательно, П. ф. пред­ставляется как физ. система с беско­нечным числом степеней свободы. По общим правилам механики можно по­лучить выражение для обобщённых импульсов П. ф. и найти плотности энергии, импульса и момента кол-ва движения поля.

Опыт показал (сначала для эл.-магн. поля), что энергия и импульс поля изменяются дискр. образом, т. е. П. ф. можно поставить в соответствие определённые ч-цы (напр., эл.-магн.

полю — фотоны, гравитационному — гравитоны). Это означает, что описа­ние П. ф. с помощью полевых ф-ций явл. лишь приближением, имеющим определённую область применимости. Чтобы учесть дискр. св-ва П. ф. (т. е. построить квант. теорию поля), необ­ходимо считать обобщённые коорди­наты и импульсы П. ф. не числами, а операторами, для к-рых выполняются определённые перестановочные соот­ношения. (Аналогично осуществляет­ся переход от классич. механики к квант. механике.)

В квант. механике доказывается, что систему взаимодействующих ч-ц мож­но описать с помощью нек-рого квант. поля (вторичное квантование). Т. о., не только каждому П. ф. соответст­вуют определённые ч-цы, но и, наобо­рот, всем известным ч-цам соответст­вуют квантованные поля. Этот факт явл. одним из проявлений корпускулярно-волнового дуализма материи. Квантованные поля описывают унич­тожение (или рождение) ч-ц и одно­временно рождение (уничтожение) ан­тичастиц. Таким полем явл., напр., электрон-позитронное поле в квант. электродинамике.

Вид перестановочных соотношений для операторов поля зависит от спина ч-ц, соответствующих данному полю. Как показал швейц. физик В. Паули (1941), для ч-ц с целым спином опера­торы поля коммутируют и ч-цы подчи­няются Бозе — Эйнштейна статис­тике, а для ч-ц с полуцелым спином — антикоммутируют и соответствующие ч-цы подчиняются Ферми — Дирака статистике. Если ч-цы подчиняются статистике Бозе — Эйнштейна (напр., фотоны и гравитоны), то в одном и том же квант. состоянии может находить­ся много (в пределе — бесконечно мно­го) ч-ц.

В указанном пределе ср. величины квант. полей переходят в обычные клас­сич. поля (напр., в классич. эл.-магн. и гравитац. поля, описываемые непре­рывными ф-циями координат и време­ни). Для полей, отвечающих ч-цам с полуцелым спином, соответствующих классич. полей не существует.

Совр. теория элем. ч-ц строится как теория взаимодействующих квант. П. ф.

• Ландау Л. Д., Л и ф ш и ц Е. М., Теория поля, 6 изд., М., 1973 (Теоретиче­ская физика, т. 2); Б о г о л ю б о в Н. Н., Ширков Д. В., Квантовые поля, М., 1980.

С. С. Герштейн.

ПОЛЯРИЗАТОР, устройство для по­лучения полностью или (реже) час­тично поляризованного оптич. излу­чения из излучения с произвольными поляризационными хар-ками (см. По­ляризация света). П.— простейший по­ляризационный прибор и один из осн. элементов более сложных таких при­боров. Линейные П., дающие плоскополяризованный свет,— либо оптически анизотропные поляризаци­онные призмы и поляроиды, либо оп­тич. стопы изотропных пластинок, прозрачных в нужной области спектра.

572


В качестве циркулярного П. для получения света, поляризованно­го по кругу, обычно применяют сово­купность линейного П. и п л а с т и н к и ч е т в е р т ь д л и н ы в о л н ы (см. Компенсатор оптиче­ский). Любой П. может быть исполь­зован и как анализатор поляризован­ного излучения. См. также Поляриза­ционные приборы.

В. С. Запасский.

ПОЛЯРИЗАЦИОННАЯ МИКРОСКО­ПИЯ, см. Микроскоп, Поляризацион­ные приборы.

ПОЛЯРИЗАЦИОННО - ОПТИЧЕСКИЙ МЕТОД ИССЛЕДОВАНИЯ напряже­ний, метод изучения напряжений в деталях машин и строит. конструкци­ях на прозрачных моделях. Основан на свойстве большинства прозрачных изотропных материалов (стекло, цел­лулоид, желатин, пластмассы — опти­чески чувствительные или пьезооптич. материалы) становиться при деформа­ции оптически анизотропными, т. е. на возникновении искусств. двойного лучепреломления (т. н. пьезооптич. эффекта). Гл. значения тензора диэлектрич. проницаемости в пределах упругости линейно связаны с гл. напряже­ниями. Так, напр., для пластинки, на­груженной в своей плоскости, одно главное напряжение ₃, направленное нормально к пластинке (рис. 1, а), равно нулю и одна из гл. плоскостей оптич. симметрии совпадает с пло­скостью пластинки.



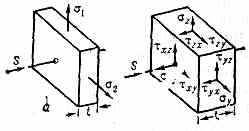
Рис. 1. Схемы: а — пластинки, нагружен­ной в своей плоскости; б — элемента объ­ёма в напряжённом состоянии; а — нормаль­ные напряжения;  — касательные напря­жения.


Если на пластинку D в круговом полярископе (рис. 2) падает свет перпендикулярно к её плоскости, то интенсивность света, прошедшего анализатор А, будет рав­на I=I₀sin/, где I₀ — интенсивность

света, прошедшего поляризатор Р,  — длина волны света лампы S поля­рископа, =Cd(₁-₂) — оптич. раз­ность хода, d — толщина пластинки, ₁ и ₂ — гл. напряжения, С — т. н. относительный оптич. коэфф. напря­жений.



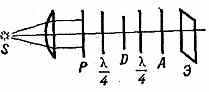
Рис. 2. Схема кругового полярископа(/4— компенсирующие пластинки; Э — экран).


Это ур-ние (т. н. ур-ние Вертгейма) — основное при решении пло­ских задач П.-о. м. и. При просвечива­нии монохроматич. светом в точках интерференц. изображения модели, в

к-рых =m, (m—целое число), на­блюдается погашение света; в точках, где =(2m+1)/2,— макс. освещён­ность. На изображении модели (рис. 3) получаются светлые и тёмные полосы разных порядков т (картина полос). Точки, лежащие на одной и той же полосе, имеют одинаковую , т. е. одинаковые ₁-₂ = 2_max = Cd (где _max — макс. касатель­ное напряжение). При белом свете точки с оди­наковыми _mах соеди­няются линиями одина­ковой окраски — изохромами. Чтобы полу­чить значения ₁-₂ (или _mах), в данной точ­ке достаточно определить С для материала модели и из­мерить компенсатором  или можно определить ₀ модели и подсчитать порядок полосы т (₀=/Сd — раз­ность гл. напряжений в модели, вы­зывающих разность хода =; С и ₀ получают при простом растяжении, сжатии или чистом изгибе образцов из материала модели).



Рис. 3. Картина полос при равномерном растягивании пластинки с круглым отвер­стием.


Т. к. при нормаль­ном просвечивании плоской модели можно получить только разность гл. напряжений и их направление, то для определения ₁ и ₂ в отдельности су­ществуют дополнит. физико-механич. способы измерения ₁+₂, а также графовычислит. методы разделения ₁ и ₂ по известным ₁-₂ и их направ­лению, использующие ур-ния механи­ки сплошной среды.

Для исследования напряжений на объёмных моделях применяется метод «замораживания» деформаций. Модель из материала, обладающего свойством «замораживания» (отверждённые эпок­сидные, фенолформальдегидные смолы и др.), нагревается до темп-ры высокоэластич. состояния, нагружается и под нагрузкой охлаждается до комнатной темп-ры (темп-ры стеклования). После снятия нагрузки деформации, возни­кающие в высокоэластичном состоя­нии, и сопровождающая их оптич. анизотропия фиксируются. «Заморо­женную» модель распиливают на тон­кие пластинки (срезы) толщиной 0,6— 2 мм, к-рые исследуют в обычном поля­рископе.

Применяется также метод рассеян­ного света, при к-ром тонкий пучок параллельных лучей поляризованного света пропускается через объёмную модель и даёт в каждой точке на своём пути рассеянный свет, к-рый наблю­дается в направлении, перпендикуляр­ном к пучку. Состояние поляризации по линии каждого луча от точки к точ­ке меняется соответственно напряже­ниям в этих точках. Существует метод, при к-ром в изготовленную из оптически нечувствительного к напряжениям прозрачного материала (спец. органич. стекла) объёмную модель вклеивают тонкие пластинки из оптически чувствит. материала. Измерения во вклей­ках проводят как на плоской моде­ли — с просвечиванием нормально или под углом к поверхности вклейки.

П.-о. м. и. применяется для изуче­ния напряжений в плоских и объём­ных деталях в пределах упругости в тех случаях, когда применение вы­числит. методов затруднено или не­возможно. П.-о. м. и. напряжений ис­пользуется для изучения пластич. деформаций (метод фотопластичности), динамич. процессов, температурных напряжений (метод фототермоупругости), для моделирования при реше­нии задач ползучести (метод фотопол­зучести) и др. нелинейных задач ме­ханики деформируемого тела.

Применяется также метод оптиче­ски чувствит. наклеек (слоев), наноси­мых на поверхности натурных дета­лей. Слой оптически чувствит. матери­ала наносится на поверхность метал­лич. детали или её модели в жидком виде и затем подвергается полимери­зации или наклеивается на деталь в виде пластинки; это обеспечивает ра­венство деформаций нагруженной де­тали и покрытия. Деформации в по­крытии определяются по измеренной в нём разности хода в отражённом све­те при помощи односторонних поляри­скопов.

Так как П.-о. м. и. напряжений ве­дётся на моделях, то он заканчи­вается переходом от напряжений в мо­дели к напряжениям в детали. В про­стейшем случае _дет=_моя•/², где  и  — масштабы геом. и силового подобий.

• Александров А. Я., А х м е т з я н о в М. X., Поляризационно-оптические методы механики деформируемого тела, М., 1973; Абен X. К., Интегральная фото­упругость, Тал., 1975; Метод фотоупруго­сти, под ред. Г. Л. Хесина, т. 1—3, М., 1975.

В. И. Савченко.