П падение тела

Вид материала

Документы

Содержание Погрешности средств измере­ний Подвижность ионов и элек­тронов Рис. 2. Зависимость подвижности ионов  Подвижность носителей тока Подводный звуковой канал ПОДДЕРЖИВАЮЩАЯ СИЛА (гидростатич. подъёмная сила, выталкиваю­щая сила, архимедова сила) Подобия критерии Рейнольдса число Re=vl/=vl!v, Маха число M=v/a Прандтля чис­ло Pr=v/a=c Фурье число Fo=at/l Подобия теория

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ (ошиб­ки измерений), отклонения резуль­татов измерений от истинных значе­ний измеряемых величин. Различают с и с т е м а т и ч е с к и е, с л у ч а й н ы е и г р у б ы е П. и. (последний вид П. и. часто наз. промахами). Систематич. П. и. обусловлены гл. обр. погрешностями средств измерений и несовершенством методов измерений (см. Измерение); случайные — рядом неконтролируемых обстоятельств (незначит. изменениями условий измере­ний и т. п.); промахи — неисправ­ностью средств измерений, неправильным отсчитыванием показаний, рез­кими изменениями условий измерений и т. д. При обработке результатов из­мерений промахи обычно отбрасывают; влияние систематич. погрешностей стремятся уменьшить внесением по­правок или умножением показаний приборов на поправочные множители; оценки случайных П. и. осуществляют методами матем. статистики. При изме­рениях пост. величин, когда исполь­зуются установившиеся показания (вы­ходные сигналы) средств измерений, П. и. наз. с т а т и ч е с к и м и. При измерениях изменяющихся величин, т. е. при изменяющихся выходных сигналах, к статич. добавляются

д и н а м и ч е с к и е П. и., и общая по­грешность возрастает.

К. П. Широков.

ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕ­НИЙ, отклонения метрологич. св-в или параметров средств измерений от номинальных, влияющие на погреш­ности результатов измерений, получае­мых при помощи этих средств. Состав­ляющие этих погрешностей, завися­щие от П. с. и., наз.

и н с т р у м е н т а л ь н ы м и п о г р е ш н о с т я м и (инструментальные ошибки). П. с. н. выражают в форме абс., относит. или приведённых погрешностей.(т. е. соот­ветственно в единицах измеряемой ве­личины, в долях или процентах от неё либо в процентах от верх. предела из­мерений, диапазона измерений или длины шкалы).

П. с. и., имеющие место при нор­мальных условиях применения средств измерений, наз.

о с н о в н ы м и; по­грешности, вызванные отклонением влияющих величин (темп-ры, частоты, электрич. напряжения и т. п.) от при­нятых за нормальные,— д о п о л н и т е л ь н ы м и. Для каждого типа средств измерений устанавливаются пределы допускаемых погрешностей, определяющие классы точности средств измерений.

• Б у р д у н Г. Д., М а р к о в Б. Н., Основы метрологии, М., 1972.

К. 77. Широков.

ПОДВИЖНОСТЬ ИОНОВ И ЭЛЕК­ТРОНОВ, 1) в газе и н и з к о т е м п е р а т у р н о й плазме — от­ношение ср. скорости v направленного движения эл-нов или ионов (в резуль­тате действия электрич. поля) к напря­жённости этого поля Е: =v/E. Зави­симость v от Е в принципе даётся ре­шением кинетич. уравнения Больц­мана. Однако не только решение, но даже точное написание этого ур-ния связано со значит. трудностями, обус­ловленными разнообразием элемен­тарных процессов, в к-рых участвуют ионы и эл-ны. Поэтому обычно П. и. и э. теоретически рассчитывают при­ближённо, вводя упрощающие допу­щения. Подвижность ионов (_i)и эл-нов (_e) исследуют раздельно, т. к. эле­ментарные процессы, определяющие движение тех и других, различны. Для эл-нов существенно, что из-за малости их массы они при упругих столкновениях с тяжёлыми ч-цами

556


теряют лишь незначит. часть энергии. Поэтому даже в слабых полях их ср. энергия намного превышает энергию тяжёлых нейтральных атомов и моле­кул. Теоретически П. и. и э. впервые проанализировал в 1903 франц. физик П. Ланжевен. Впоследствии были раз­виты более строгие и сложные теории зависимости v от Е. Первым измерил _e англ. физик Дж. Таунсенд, изучая диффузию пучка эл-нов, движущихся в электрич. поле, и смещение этого пучка в магн. поле. Данные о зависи­мости v эл-нов от E в разл. газах при­ведены на рис. 1. Приближённые зна­чения _e получают при измерении кон­центрации и энергии эл-нов (а также Е) в положительном столбе газового разряда.



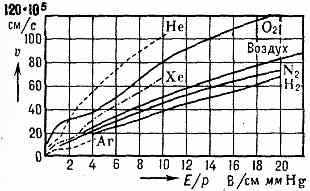
Рис. 1. Зависимость скорости в направлен­ного (по электрич. полю Е) движения эл-нов в разл. газах от отношения Е/р, где р — приведённое к 0°С давление газа.


Подвижность ионов в постороннем газе удовлетворительно описывается теорией Ланжевена, согласно к-рой в однородном газе она зависит только от массы иона (рис. 2).



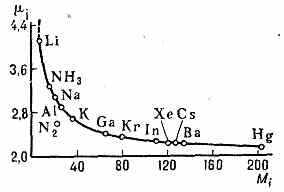
Рис. 2. Зависимость подвижности ионов _i от их массы M_i.

Осн. процесс, определяющий _i ионов в их собств. газе,— перезарядка ионов. При столк­новении с нейтральной ч-цей ион обме­нивается с ней зарядом, а вновь воз­никший ион «стартует» (т. н. эстафет­ное движение ионов).

П. и. и э. связана с коэфф. диффузии D ф-лой Эйнштейна: D/= kT/e, где Т — абс. темп-pa заряженных ч-ц в предположении, что они подчиняются Максвелла распределению (в смеси раз­ных заряженных и нейтральных ч-ц их ср. энергии и, следовательно, темп-ры могут быть различны — св-во «неизотермичности» такой смеси); е — заряд эл-на.

2) Подвижность ионов в растворах U=Fu, где F — Фарадея постоянная, u — скорость иона в см/с при напря­жённости электрич. поля в 1 В/см. Величина U зависит от природы иона, а также от темп-ры, диэлектрической

проницаемости, вязкости и концентра­ции раствора.

• См. лит. при ст. Рекомбинация ионов и электронов.

ПОДВИЖНОСТЬ НОСИТЕЛЕЙ ТОКА в твёрдом теле, отношение скорости направленного движения носителей за­ряда в тв. проводниках (д р е й ф о в о й с к о р о с т и v_др), вызванного электрич. полем, к напряжённости Е этого поля:

=v_др/E. (1)

У разных типов носителей в одном и том же в-ве  различны, а в анизотроп­ных кристаллах различны  каждого типа носителей для разных направле­ний поля Е. Подвижность эл-нов про­водимости и дырок определяется про­цессами рассеяния эл-нов в кристалле. Рассеяние происходит на дефектах кристаллич. решётки, а также на её тепловых колебаниях (фононах). Ис­пуская или поглощая фонон, носитель изменяет свой квазиимпульс, а, следо­вательно, и скорость. Поэтому  силь­но зависит от темп-ры. При комнатных темп-pax (Т300 К), как правило, преобладает рассеяние на фононах, с понижением темп-ры вероятность это­го процесса падает, и доминирующим становится рассеяние на дефектах (осо­бенно заряженных), вероятность к-рого растёт с уменьшением энергии носи­телей.

Ср. дрейфовая скорость v_др равна: у_др=еE/m*, где е — заряд, m* — эффективная масса, — интервал вре­мени между двумя последоват. актами рассеяния (в р е м я с в о б о д н о г о п р о б е г а). Отсюда:

=е/m*. (2)

П. н. т. в тв. проводниках варьирует­ся в широких пределах — от 10⁵ см²/с до 10^-3 см²/с и меньше при T=300 К. В переменном электрич. поле v_др может не совпадать по фазе с напря­жённостью поля Е, и тогда П. н. т. бу­дет зависеть от частоты поля.

• Блатт Ф.-Дж., Теория подвижности электронов в твердых телах, пер. с англ., М.—Л., 1963.

Э. М. Эпштейн.

ПОДВОДНЫЙ ЗВУКОВОЙ КАНАЛ, слой в океане, расположенный на нек-рой глубине, в к-ром наблюдается сверхдальнее распространение звука под водой, обусловленное рефракцией звука. Подробнее см. Гидроакустика.

ПОДДЕРЖИВАЮЩАЯ СИЛА (гидростатич. подъёмная сила, выталкиваю­щая сила, архимедова сила), направ­ленная вертикально вверх составляю­щая суммы сил давления жидкой или газообразной среды на поверхность тела, полностью или частично погру­жённого в среду (см. Архимеда закон).

ПОДОБИЯ КРИТЕРИИ, безразмер­ные (отвлечённые) числа, составленные из размерных физ. параметров, опре­деляющих рассматриваемые физ. яв­ления. Равенство всех однотипных П. к. для двух физ. явлений и систем — необходимое и достаточное условие физ. подобия этих систем. П. к., пред­ставляющие собой отношения однород­ных физ. параметров системы (напр.,

отношения длин), наз.. тривиальными и при установлении определяющих П. к. обычно не рассматриваются: равенство их для двух систем явл. определением физ. подобия. Нетриви­альные безразмерные комбинации, к-рые можно составить из определяю­щих параметров, и представляют собой П. к. Всякая новая комбинация из П. к. также явл. П. к., что даёт воз­можность в каждом конкретном случае выбрать наиболее удобные и характер­ные критерии. Число определяющих нетривиальных П. к. меньше числа определяющих физ. параметров с разл. размерностями на величину, равную числу определяющих параметров с не­зависимыми размерностями. Подроб­нее см. Подобия теория.

Если известны ур-ния, описывающие рассматриваемое физ. явление, то П. к. для этого явления можно получить, приводя ур-ния к безразмерному виду путём введения нек-рых характерных значений для каждого из определяю­щих физ. параметров, входящих в сис­тему ур-ний. Тогда П. к. определяют­ся как безразмерные коэфф., появляю­щиеся перед нек-рыми из членов новой системы безразмерных ур-ний. Когда ур-ния, описывающие физ. явление, неизвестны, П. к. отыскиваются при помощи анализа размерностей, опре­деляющих физ. параметры (см. Раз­мерностей анализ).

П. к. механич. движения получается из ур-ния, выражающего второй закон Ньютона, и наз. числом Ньютона Ne=Ft²/ml, где F — действующая на тело сила, т — его масса, t — время, l — характерный линейный размер.

При изучении упругих деформаций конструкции под воздействием внеш. сил основными П. к. явл. Пуассона коэффициент для материала конструк­ции v=|₁/₂| и критерии gl/E, F/El², где =L/L — относит. продольная деформация, ₁=d/d — относит. по­перечная деформация, Е — модуль Юнга,  — плотность материала кон­струкции, F — характерная внеш. си­ла, g — ускорение силы тяжести.

В г и д р о а э р о м е х а н и к е важнейшие П. к.— Рейнольдса число Re=vl/=vl!v, Маха число M=v/a и Фруда число Fr=v²/gl, где  — плот­ность жидкости или газа, v — скорость течения,  — динамич. коэфф. вяз­кости, v=/— кинематич. коэфф. вязкости, а — местная скорость рас­пространения звука в движущейся среде. Каждый из П. к. имеет опреде­лённый физ. смысл как величина, пропорциональная отношению одно­типных физ. величин. Так, число Re характеризует отношение инерцион­ных сил при движении жидкости или газа к силам вязкости, а число Fr — отношение инерционных сил к силам тяжести.

Основными П. к. процессов тепло­передачи между жидкостью (газом) и

557


обтекаемым телом явл. Прандтля чис­ло Pr=v/a=c_p/, Нуссельта чис­ло Nu=l/, Грасгофа число Gr=gl³T/v², Пекле число Pe=vl/a и Стэнтона число St=/c_pv. Здесь  — коэфф. теплопередачи,  — коэфф. теп­лопроводности, c_р — удельная тепло­ёмкость жидкости или газа при пост. давлении, а=/с_р — коэфф. темпера­туропроводности,  — коэфф. объём­ного расширения, T — разность темп-р поверхности тела и жидкости (газа). Два последних числа связаны с предыдущими соотношениями: Ре=Pr•Re, St=Nu/Pe.

Для процессов теплопроводности в тв. телах характерны П. к.: Фурье число Fo=at/l² и число Био Bi=l/. Число Bi определяет характер соот­ветствия между температурными усло­виями в окружающей среде и распре­делением темп-ры в теле.

В процессах, изменяющихся с тече­нием времени t, основным П. к., характеризующим одинаковость проте­кания процессов во времени, явл. кри­терий гомохронностп Ho=vt/l. В зада­чах гидроаэромеханики нестационар­ных течений этот критерий обычно наз. Струхаля числом Sh. Критерий гомохронности в случае подобия электродинамич. явлений записывают в виде Ho=t, где  — характерная частота.

Примером П. к. эл.-магн. полей служат критерии: l²/t и /t, где  — магн. проницаемость среды,  — её удельная проводимость,  — диэлектрич. проницаемость среды, а в случае подобия электрич. цепей с распреде­лёнными параметрами — критерии: L/Rt и C/Gt, где L — индуктивность, R — сопротивление, С — ёмкость, G — проводимость.

• См. лит. при ст. Подобия теория.

С. Л. Вишневецкий.

ПОДОБИЯ ТЕОРИЯ, учение об ус­ловиях подобия физ. явлений. Опи­рается на учение о размерности физ. величин (см. Размерностей анализ) и служит основой моделирования. Предметом П. т. явл. установление критериев подобия разл. физ. явлений и изучение с помощью этих критериев св-в самих явлений.

Физ. явления, процессы или систе­мы подобны, если в сходственные мо­менты времени в сходственных точках пространства значения переменных ве­личин, характеризующих состояние одной системы, пропорциональны соответств. величинам другой системы. Коэфф. пропорциональности для каж­дой из величин наз. коэфф. подобия. Физ. подобие явл. обобщением эле­ментарного и наглядного понятия геом. подобия. При геом. подобии су­ществует пропорциональность (подо­бие) сходственных геом. элементов подобных фигур или тел. При физ. по­добии поля соответств. физ. парамет­ров двух систем подобны в пространст­ве и времени. Напр., при кинематич.

подобии существует подобие полей ско­рости для двух рассматриваемых дви­жений; при динамич. подобии реали­зуется подобие систем действующих сил или силовых полей разл. физ. природы (силы тяжести, силы давле­ния, силы вязкости и т. п.); механич. подобие (напр., подобие двух потоков жидкости или газа, подобие двух упру­гих систем и т. п.) предполагает нали­чие геом., кинематич. и динамич. по­добий; при подобии тепловых процес­сов подобны соответств. поля темп-р и тепловых потоков; при электродинамич. подобии — поля токов, нагрузок, мощностей, поля эл.-магн. сил. Все перечисленные виды подобия — част­ные случаи физ. подобия. С развитием исследований сложных физ. и физ.-хим. процессов, включающих меха­нич., тепловые и хим. явления, разви­ваются и методы П. т. для этих про­цессов, напр. устанавливаются усло­вия подобия процессов трения и изно­са деталей машин, кинетики физ.-хим. превращений и др. явлений. Пропорци­ональность для подобных явлений всех характеризующих их параметров приводит к тому, что все безразмерные комбинации, к-рые можно составить из этих параметров, имеют для подоб­ных явлений одинаковые численные значения. Безразмерные комбинации, составленные из определяющих пара­метров рассматриваемых явлений, наз. подобия критериями. Любая комби­нация из критериев подобия также представляет собой критерий подобия рассматриваемых физ. явлений.

Если в рассматриваемых физ. яв­лениях или системах существует ра­венство не всех, а лишь нек-рых неза­висимых критериев подобия, то гово­рят о неполном, или частичном, по­добии. Такой случай наиболее часто встречается на практике. При этом существенно, чтобы влияние на проте­кание рассматриваемых физ. процес­сов критериев, равенство к-рых не соблюдается, было незначительным или малосущественным.

Размерные физ. параметры, входя­щие в критерии подобия, могут при­нимать для подобных систем сильно различающиеся значения; одинаковы­ми должны быть лишь безразмерные критерии подобия. Это св-во подобных систем и составляет основу моделиро­вания. С. Л. Вишневский.

Ниже более строго излагаются логич. основы П. т. Предположим, что для описания изучаемых явлений упо­требляются r основных независимых единиц измерения А₁, А₂, . . ., А_r (напр., в абс. системах единиц основ­ными явл. единицы длины L, массы М и времени Т). Производные единицы образуются из основных согласно со­отношению Q=A^p1₁A^p2₂. . .А^pr_r. Их раз­мерность [Q]=[A^p1₁A^p2₂. . .А^pr_r] харак­теризуется числовыми показателями p₁, p₂, . . , p_r. Каждая величина X размерности [Х]=[Q] может быть представлена в виде: X=xQ, где х — числовое выражение величины X при выбранной системе основных величин A₁, А ₂, . . ., А_r.

Пусть изучается класс явлений S, каждое из к-рых определяется зада­нием определённых значений системы величин {Y_}. Два таких явления S⁽¹⁾ и S⁽²⁾ наз. подобными, если значения величин Y_⁽²⁾, характе­ризующие явление S⁽²⁾, получаются из значений соответств. величин Y⁽¹⁾_, характеризующих явление S⁽¹⁾, по формулам: Y²_=k^p1₁k^p2₂. . .k^Pr_rY⁽¹⁾_, где коэфф. подобия k_t, k₂, . . ., k_r постоян­ны, а показатели p₁, р₂, . . ., р_r опре­деляются размерностью [Y_]=[А^p1₁А^p2₂. . .А^pr_r] величин Y_.

Предположим, что из системы ве­личин {Y_} выделена нек-рая часть, образующая систему {Х_} определяю­щих параметров, так что числовое значение y_ любой величины Y_ явл. функцией y_=f_{x_} числовых значе­ний х_ величин Х_ и вид функциональ­ных зависимостей f_ остаётся одним и тем же при любом выборе основных единиц измерения A₁, А₂, ..., А_r. В этом предположении основной прин­цип П. т. может быть сформулирован след. образом. Для подобия явлений S⁽¹⁾ и S⁽²⁾ необходимо и достаточно, чтобы значения любой безразмерной комбинации



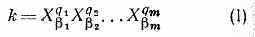
определяющих параметров в явлениях S⁽¹⁾ и S⁽²⁾ были равны: k⁽¹⁾=k⁽²⁾.

Каждое безразмерное выражение k вида (1) наз. к р и т е р и е м п о д о б и я. Очевидно, что при таком опреде­лении критериев подобия в их число попадают все безразмерные опреде­ляющие параметры и все отношения вида:

k=X_1/X_2, (2)

где Х_1 и X_2 — определяющие пара­метры одной и той же размерности.

Необходимость для подобия равенств k⁽¹⁾=k⁽²⁾ в применении к безразмер­ным параметрам и отношениям вида (2) очевидна непосредственно. Их мож­но называть тривиальными. Сами от­ношения вида (2) при перечислении критериев подобия часто опускают. Если тривиальные условия k⁽¹⁾=k⁽²⁾ считаются заведомо выполненными, то среди нетривиальных условий подо­бия k⁽¹⁾ =k⁽²⁾ имеется только s=n-r' независимых, где n — число разл. размерностей величин системы {Х_}, а r' — Число независимых размерно­стей среди этих n размерностей. Т. к. всегда r'r, то sn-r.

Напр., геом. картина стационарного обтекания прямоугольной пластинки, помещённой в однородный неограни­ченный поток вязкой несжимаемой жидкости со скоростью на бесконеч­ности, параллельной продольной сто­роне пластинки, определяется: 1) дли­ной пластинки l; 2) её шириной b; 3) скоростью потока на бесконечности

558


v, 4) кинематич. коэфф. вязкости . Т. к. [b] =[l] и [] = [vl], то среди трёх размерностей определяющих па­раметров имеются лишь две независи­мые, т.е. r'=2 и s=n-r'=3-2=1. В соответствии с этим имеется один нетривиальный критерий подобия — Рейнольдса число Re=vl/. Кроме того, имеется один тривиальный геом. кри­терий подобия b/l. Если исследуемые явления изучаются при помощи дифф. ур-ний, то определяющие параметры появляются: 1) в виде величин, входя­щих в начальные и граничные усло­вия; 2) в виде коэфф., входящих в дифф. ур-ния. После приведения ур-ний к безразмерному виду в них ос­таются лишь безразмерные коэфф., к-рые и явл. критериями подобия. А. Н. Колмогоров.

Практич. применения П. т. весьма обширны. Она даёт возможность пред­варительного качественно-теоретич. анализа и выбора системы определяю­щих безразмерных параметров слож­ных физ. явлений. П. т.— основа для правильной постановки и обработки результатов экспериментов. В сочета­нии с дополнит. соображениями, по­лученными из эксперимента или из ур-ний, описывающих физ. явление, П. т. приводит к новым существ. ре­зультатам.

• Седов Л. И., Методы подобия и раз­мерности в механике, 9 изд., М., 1981; Э й г е н с о н Л. С., Моделирование, М., 1952; Веников В. А., Теория подобия и мо­делирование (Применительно к задачам электроэнергетики), 2 изд., М., 1976; К и р п и ч е в М. В., Теория подобия, М., 1953; Дьяконов Г. К., Вопросы теории по­добия в области физико-химических процес­сов, М., 1956.