П падение тела

Вид материала

Документы

Содержание Подрешётка магнитная Подхвата реакция Подъёмная сила Рис. 1. Обтекание профиля крыла самолёта. Скорость v Г имеет размерность [v•l Рис. 2. Зависимость c М набегаю­щего потока, при к-ром вблизи поверх­ности профиля местные значения чис­ла M=1) Рис. 3. Схема сверхзвукового обтекания пла­стинки: v М. Я. Юделоеич. Дирака уравнения Э. А. Тагиров. Пойнтинга вектор Показатель преломления Поле зрения Изображение оптическое) Полевая ионизация В. М. Розенберг. А. Л. Ройтбурд. Т=0К определяется минимумом внутр. энергии Н А. Л. Ройтбурд. ... Полное содержание

Подобный материал:

• Тема «кинематика материальной точки», 29.33kb.
• Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
• Программа вступительных испытаний по физике механика, 48.4kb.
• Тема: строение тела животных, 47.92kb.
• Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
• Тема. Малые тела Солнечной системы, 383.39kb.
• Книга о душе, 521.77kb.
• Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
• Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.

ПОДРЕШЁТКА МАГНИТНАЯ, сис­тема периодически расположенных в пространстве одинаковых магн. ато­мов или ионов, имеющих одинаковые по величине и направлению магнит­ные моменты. П. м. рассматривают при описании магнитной структуры атомной антиферромагнетиков и ферримагнетиков. Трансляционные пери­оды магн. подрешёток могут совпадать с периодом кристаллографич. струк­туры, но могут быть и кратны им. В последнем случае магн. элементар­ная ячейка не совпадает с кристалло­графической. Существование П. м. до­казано опытами по дифракции нейтро­нов на магн. структурах.

ПОДХВАТА РЕАКЦИЯ, ядерная ре­акция, при к-рой налетающая ч-ца «подхватывает» нуклон из ядра мише­ни и образует с ним связанную систему (ядро), напр, (р, d).

ПОДЪЁМНАЯ СИЛА, составляющая полной силы давления жидкой или газообразной среды на движущееся в ней тело, направленная перпендику­лярно к скорости тела (к скорости центра тяжести тела, если оно движет­ся непоступательно). Возникает П. с. вследствие несимметрии обтекания те­ла. Напр., несимметричное обтекание крыла (рис. 1) можно представить как результат наложения на симметрич­ное течение циркуляционного потока

вокруг контура крыла, что приводит к увеличению скорости на одной сто­роне крыла и к её уменьшению на про­тивоположной стороне. Тогда П. с. Y будет зависеть от величины циркуля­ции скорости Г и, согласно Жуков­ского теореме, для участка крыла дли­ной L (вдоль размаха), обтекаемого



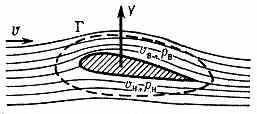
Рис. 1. Обтекание профиля крыла самолёта. Скорость v_{н в}. давление p_н>p_в, Y — подъёмная сила крыла.

плоскопараллельным потоком идеаль­ный несжимаемой жидкости, У= vГL, где  — плотность среды, v — скорость набегающего потока.

Поскольку Г имеет размерность [v•l], то П. с. можно выразить равенст­вом Y=c_ySv²/2, обычно применяемым в аэродинамике, где S — величина характерной для тела площади (напр., площадь крыла в плане, равная L•b, если b — длина хорды профиля кры­ла), Су — безразмерный коэфф. П. с., зависящий, в общем случае, от формы тела, его ориентации в среде и чисел Рейнольдса Re и Маха М. Значение Су определяют теор. расчётом или экс­периментально., Так, согласно теории Жуковского, для крыла в плоскопа­раллельном потоке при небольших углах атаки c_y=2m(-₀), где  — угол атаки (угол между направлением скорости набегающего потока и хордой крыла), ₀ — угол нулевой П. с., m — коэфф., зависящий только от формы профиля крыла, напр, для тонкой сла­бо изогнутой плас­тины m=. В слу­чае крыла конечно­го размаха L ко­эфф. m=(1-2/), где =L/b — удли­нение крыла.

В реальной жид­кости в результате



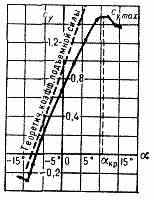
Рис. 2. Зависимость c_y от .


влияния вязкости величина т меньше теоретической, причём эта разница возрастает по мере увеличения отно­сит. толщины профиля; значение угла ₀ также меньше теоретического. Кро­ме того, с увеличением угла а зависи­мость Су от а (рис. 2) перестаёт быть линейной и величина dc_y/d монотонно убывает, становясь равной нулю при угле атаки _кр, к-рому соответствует макс. величина коэфф. П. с.— c_{y, max}. Дальнейшее увеличение а ведёт к па­дению Су вследствие отрыва погранич­ного слоя от верхней поверхности крыла и возрастания давления на ней. Величина с_у, _max имеет существ. зна­чение, т. к. чем она больше, тем мень­ше скорость взлёта и посадки само­лёта.

При больших, но докритич. скорос­тях, т. е. таких, для к-рых Мкр (М_кр — значение числа М набегаю­щего потока, при к-ром вблизи поверх­ности профиля местные значения чис­ла M=1), становится существенной сжимаемость газа. Для слабо изогну­тых и тонких профилей при малых углах атаки сжимаемость можно при­ближённо учесть, положив

'=/(1-M²), с_у=(c_y)_несж/(1-M²)

При сверхзвуковых скоростях ха­рактер обтекания существенно меня­ется. Так, при обтекании плоской пла­стины у передней кромки на верхней поверхности образуются волны раз­режения, а на нижней — ударная вол­на (рис. 3). В результате давление р_н на нижней поверхности пластины становится больше, чем на верхней (р_в); возникает суммарная сила, нормаль­ная к поверхности пластины, состав­ляющая к-рой, перпендикулярная к скорости набегающего потока, и есть П. с.



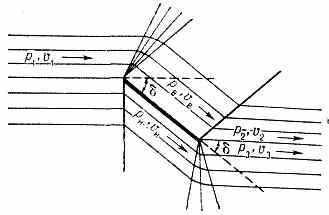
Рис. 3. Схема сверхзвукового обтекания пла­стинки: v_в>v₁, р_в1; v_2в,

р₂>p_в; v_н1, p_н>р₁, v₃>v_н, p_3н.

Для малых М>1 и малых а П. с. пластины может быть вычислена по ф-ле c_y=4/(M²-1). Эта ф-ла спра­ведлива и для тонких профилей произ­вольной формы с острой передней кромкой.

• Жуковский Н. Е., Собр. соч., т. 6— Теоретические основы воздухоплава­ния, М.—Л., 1950; Л о й ц я н с к и й Л. Г., Механика жидкости и газа, 5 изд., М., 1978.

М. Я. Юделоеич.

ПОЗИТРОН (е⁺ ) [от лат. posi(tivus) — положительный и (элек)трон], элемен­тарная частица с положит. электрич. зарядом, античастица по отношению к эл-ну (е^-). Массы (m_е) и спины (J) П. и эл-на равны, а их электрич. за­ряды (е) и магн. моменты (_е) равны по абс. величине, но противоположны по знаку: m_e~9,l•10^-28 г, J=¹/₂ (в ед. постоянной Планка ћ), e4,8X10^-10 СГСЭ единиц, _e= 1,00116 (в ед. магнетона Вора).

Теоретически существование поло­жительно заряж. «двойника» эл-на следует из Дирака уравнения; эта возможность была указана англ. физиком П. Дираком в 1931. В 1932 амер. физик К. Д. Андерсон экспери­ментально обнаружил такую ч-цу в космических лучах и назвал её П.

559


Открытие П. имело фундам. значение: в отличие от известных к сер. 1932 эл-на, протона и нейтрона, П. не вхо­дил в состав «обычного» в-ва на Зем­ле,— возникли понятия античастицы и антивещества. Предсказанные Ди­раком и наблюдённые на опыте в 1933 процессы аннигиляции пары и рожде­ния пары е⁺е^- были первыми убедит. проявлениями взаимопревращаемости элем. ч-ц.

П. участвует в эл.-магн., слабом и гравитац. вз-ствиях и относится к классу лептонов. По статистич. св-вам он является фермионом. П. стабилен, но в в-ве существует короткое время из-за аннигиляции с эл-нами; напр., в свинце П. аннигилируют в среднем за 5•10^-11 с. При определённых усло­виях, прежде чем аннигилировать, П. и эл-н могут образовать свя­занную систему — позитроний.

П. образуются при взаимопревра­щениях свободных элем. ч-ц (напр., при распадах положит. мюона, в процессах рождения пар е⁺е^- -квантами в электростатич. поле ат. ядра), при бета-распаде нек-рых радиоактив­ных изотопов. П., получаемые при -распаде и рождении пар, использу­ются для исследоват. целей: изучение процессов замедления П. в в-ве и их последующей аннигиляции даёт ин­формацию о физ. и хим. св-вах в-ва, напр. о распределении скоростей эл-нов проводимости, о дефектах крист. решётки, о кинетике нек-рых типов хим. реакций. Один из методов иссле­дования элем. ч-ц при сверхвысоких энергиях основан на столкновении встречных пучков ускоренных П. и эл-пов.

• Д и р а к П. А. М., Принципы кванто­вой механики, пер. с англ., М., 1960; Г о л ь д а н с к и й В. И., Физическая химия по­зитрона и позитрония, М., 1968.

Э. А. Тагиров.

ПОЗИТРОНИЙ (хим. символ Ps), свя­занная водородоподобная система е⁺е^- , состоящая из эл-на и позитрона. Размеры П. примерно в два раза пре­вышают размеры атома водорода (т. к. приведённая масса П. равна ¹/₂m_е, где m_e — масса эл-на), а его энергия связи в два раза меньше. П. образует­ся при столкновениях медленных по­зитронов с атомами в-ва и захвате по­зитроном ат. эл-на. В зависимости от взаимной ориентации спинов эл-на и позитрона различают о р т о п о з и т р о н и й (спины е⁺ и е^- параллель­ны) и парапозитроний (спины антипараллельны). П.— нестабиль­ная система, т. к. эл-н и позитрон очень быстро аннигилируют в -кванты: в силу сохранения зарядовой чёт­ности парапозитроний аннигилирует в два -кванта (за время 1,25•10^-10 с), а ортопозитроний — в три -кванта (за время 1,4•10^-7 с). Уровень парапозитрония на 8,41•10^-4эВ ниже уров­ня ортопозитрония, и в магн. поле между ними возможны переходы. Поскольку П.— простейшая система, свя­занная чисто эл.-магн.- силами, без примеси сильного вз-ствия, изучение св-в свободного П. представляет осо­бый интерес для проверки справедли­вости квантовой электродинамики. Ре­зультаты расчётов св-в П. прекрасно согласуются с данными опытов.

Св-ва П. и, в частности, время его жизни в в-ве отличаются от хар-к свободного П. и зависят от св-в в-ва. Это позволяет использовать П. для изучения физико-хим. особенностей структуры в-в, напр. исследовать с его помощью быстрые хим. реакции, ско­рость протекания к-рых сравнима со временем жизни П. Для этого изме­ряют, напр., изменение времени жиз­ни П. или величину расщепления энергий орто- и парасостояний.

• Гольданский В. И., Физическая химия позитрона и позитрония, М., 1968; Г о л ь д а н с к и й В. И., Фирсов В. Г., Химия новых атомов, «Успехи хи­мии», 1971, т. 40, в. 8.

Л. И. Пономарёв.

ПОЙНТИНГА ВЕКТОР, вектор плот­ности потока эл.-магн. энергии. Наз­ван по имени англ. физика Дж. Г. Пойнтинга (J. H. Poynting). Модуль П. в. равен энергии, переносимой за ед. времени через ед. площади поверх­ности, перпендикулярной к направле­нию распространения эл.-магн. энер­гии (т. е. к направлению П. в.). В абс. (Гаусса) системе единиц П. в. П=(c/4)[ЕН], где [EH] -— векторное про­изведение напряжённостей электрич. Е и магн. Н полей, с — скорость света в вакууме; в СИ П=[EH]. Поток П. в. через замкнутую поверхность, ограни­чивающую систему заряж. ч-ц, даёт величину энергии, теряемой системой за ед. времени вследствие излучения эл.-магн. волн (см. Максвелла уравне­ния). Плотность импульса эл.-магн. поля g выражается через П. в.:

g=(1/c²)П.

Г. Я. Мякишев.

ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ, см. Преломления показатель.

ПОККЕЛЬСА ЭФФЕКТ, линейный электрооптич. эффект, изменение по­казателя преломления света в кристал­лах, помещённых в электрич. поле, пропорциональное напряжённости приложенного поля. Как следствие этого эффекта в кристаллах появляет­ся двойное лучепреломление или ме­няется его величина. П. э. наблюдает­ся только у пьезоэлектриков. Был об­наружен в 1894 нем. физиком Ф. Поккельсом (F. Pockels), затем длит. время исследовался мало и находил ограни­ченное применение. Гл. причина — высокие электрич. напряжения (десят­ки и сотни кВ) для получения замет­ного эффекта.

Появление лазеров стимулировало исследования П. э. В последние деся­тилетия было обнаружено и исследова­но большое число крист. систем, об­ладающих большим линейным элект­рооптич. эффектом и, соответственно, требующих малых управляющих на­пряжений (порядка десятков или сотен

вольт). На основе П. э. разработан ряд устройств управления когерентным оп­тич. излучением. Почти все созданные модуляторы света (см. Модуляция света) основаны на П. э. Важное свойство П. э.— малая инерцион­ность, позволяющая осуществлять мо­дуляцию света до частот ~10¹³ Гц. Кроме того, из-за линейной зависимо­сти между показателем преломления и напряжённостью электрич. поля нелинейные искажения при модуля­ции света относительно невелики. Ма­лая инерционность позволяет исполь­зовать П. э. для модуляции добротно­сти лазеров, с помощью к-рой получа­ют г и г а н т с к и е по мощности световые импульсы малой длительно­сти. П. э. находит применение также в системах углового отклонения све­тового пучка и в устройствах создания двумерного оптич. изображения.

• С о н и н А. С., Василевская A. С., Электрооптические кристаллы, М., 1971; Мустель Е. Р., Парыгин B.Н., Методы модуляции и сканирования света, М., 1970.

В. Н. Парыгин.

ПОЛЕ ЗРЕНИЯ оптической системы, часть пространства (или плоскости), изображаемая оптич. .системой. П. з. определяется контурами оптич. дета­лей (такими, как оправы линз, призм), диафрагмами и т. п., к-рые ограничи­вают световые пучки. Величина П. з.



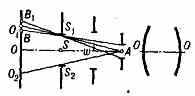
определяется тем из этих контуров S₁S₂ (рис.), к-рый виден из центра А входного зрачка (см. Диа­фрагма в оптике) под наименьшим уг­лом (этот контур наз. в х о д н ы м л ю к о м). Величина П. з. измеряется либо углом 2w, под к-рым виден вход­ной люк S₁S₂ и соответствующая часть предмета O₁O₂ из центра входного зрач­ка (у г л о в о е П. з.), либо линейны­ми размерами этой части O₁O₂ (линей­ное П. з.). Системы, предназначенные для наблюдения за удалёнными объек­тами (телескопы, зрительные трубы), обычно характеризуют угловым П. з., а системы, в к-рых расстояние до объ­екта невелико (напр., микроскопы),— линейным П. з.

В общем случае плоскости объекта O₁О₂ и входного люка S₁S₂ не совпа­дают и имеет место виньетирование (с шириной кольца ВВ₁, рис.). Если же плоскость S₁S₂ совмещена с плоскостью объекта, граница П. з. р е з к а. Этого стараются добиться во мн. телескопах, зрительных трубах и др., помещая диафрагму П. з. в фокальную плоскость объектива.

Угол П. з. в пространстве предметов (см. Изображение оптическое) обратно пропорционален увеличению оптиче­скому системы; так, в биноклях он со­ставляет 5—10°, а в самых больших телескопах не превышает неск. угло­вых мин. В широкоугольных фото-

560


объективах он достигает 120—140° и даже 180°. П. з. микроскопа опреде­ляется отношением П. з. окуляра 2l к линейному увеличению объектива

:2l/.

Г. Г. Слюсарев.

ПОЛЕВАЯ ИОНИЗАЦИЯ, то же, что автоионизация.

ПОЛЕВАЯ ЭМИССИЯ, то же, что автоэлектронная эмиссия.

ПОЛЗУЧЕСТЬ МАТЕРИАЛОВ, мед­ленная непрерывная пластич. дефор­мация тв. тела под воздействием пос­тоянной нагрузки или механич. на­пряжения. П. м. в той или иной мере подвержены все тв. тела — как кри­сталлические, так и аморфные, под­вергнутые любому виду нагружений. П. м. имеет место при темп-pax от кри­огенных до темп-р, близких к темп-ре плавления. Поскольку деформация и скорость П. м. увеличиваются с воз­растанием темп-ры, то её вредные по­следствия особенно проявляются при



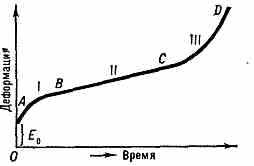
Кривая ползучести: АВ — участок неуста­новившейся (или затухающей) ползучести (I стадия); ВС — участок установившейся ползучести — деформации, идущей с посто­янной скоростью (II стадия); CD — участок ускоренной ползучести (III стадия); Е₀ — деформация в момент приложения нагрузки; точка D — момент разрушения.


повыш. темп-pax. П. м. описывается т. н. кривой ползучести (рис.), к-рая представляет собой зави­симость деформации от времени при постоянных темп-ре и приложенной нагрузке (или напряжении). Кривая П. м. имеет одинаковый вид для ши­рокого круга материалов — металлов и сплавов, ионных кристаллов, полу­проводников, полимеров, льда и др. тв. тел. Структурный же механизм П. м., т. е. элементарные процессы, приводящие к П. м., зависят как от вида материала, так и от условий, в к-рых происходит ползучесть. Осн. ме­ханизмом П. м. (за исключением аморф­ных тел) явл. перемещение дислока­ций и др. дефектов крист. решётки под воздействием механич. напряжений и темп-ры.

Высокое сопротивление П. м. явл. одним из факторов, определяющих жаропрочность. Для сравнит. оценки технич. материалов сопротивление пол­зучести характеризуют пределом ползучести — напряжением, при к-ром за данное время достигается де­формация определённой величины. Иногда сопротивление П. м. характе­ризуют величиной скорости деформа­ции по прошествии заданного времени.

• Р е г е л ь В. Р., С л у ц к е р А. И., Томашевский Э. Е., Кинетическая природа прочности твердых тел, М., 1974; Розенберг В. М., Основы жаропроч­ности металлических материалов, М., 1973.

В. М. Розенберг.

ПОЛИКРИСТАЛЛ, агрегат мелких монокристаллов разл. ориентации (крист. зёрен). Большинство тв. тел (минералы, металлы, сплавы, керамики и др.) имеют поликрист. строение. Св-ва П. обусловлены ср. размером зёрен (от 1— 2•10^-6 м до неск. мм), их ориента­цией и межзёренными границами. Если зёрна ориентированы хаотиче­ски, а их размеры малы по сравнению с размером П., то в П. не проявляется анизотропия св-в, характерная для монокристаллов. Если есть преиму­ществ. кристаллографич. ориентация зёрен, то П. явл. текстурированным (см. Текстура) и в этом случае он об­ладает анизотропией. Наличие межзёренных границ существенно сказы­вается на физ., особенно механич. св-вах П., т. к. на них происходит рассеяние электронов проводимости и фононов, торможение дислокаций, зарождение трещин и т. п.

П. образуются при кристаллизации, полиморфных превращениях (см. По­лиморфизм), а также в результате спекания крист. порошков. При дли­тельном отжиге металлич. П. проис­ходит преимуществ. рост отд. зёрен за счёт других (рекристаллизация), приводящий к образованию крупно­зернистых П. или монокристаллов. • См. лит. при ст. Кристаллы.

А. Л. Ройтбурд.

ПОЛИМОРФИЗМ (от греч. polymorphos — многообразный), способность нек-рых в-в существовать в состояниях с разл. атомно-крист. структурой (см. Кристаллохимия). Каждое из таких состояний (термодинамич. фаз), наз. п о л и м о р ф н о й м о д и ф и к а ц и е й, устойчиво при определённых внеш. условиях (темп-ре и давлении). Различие в структуре обусловливает и различие в св-вах полиморфных мо­дификаций данного в-ва. П. был от­крыт в 1822 нем. учёным Э. Мичерлихом. Им обладают нек-рые простые в-ва (аллотропия) и мн. соеди­нения. Так, 2 модификации угле­рода — кубическая (алмаз) и гекса­гональная (графит), резко разли­чаются по физ. св-вам. Белое олово, имеющее тетрагональную объ­ёмно-центрированную кристалличе­скую решётку,— пластичный металл, а серое олово (низкотемпературная модификация) с алмазоподобной тетра­гональной решёткой — хрупкий полу­проводник. Нек-рые в-ва, напр. сера и кремнезём, имеют больше чем две полимерные модификации. П. наблю­дается и в жидких кристаллах.

Области устойчивости полиморфных модификаций и точки перехода между ними определяются фазовыми диаграм­мами равновесия, расчёт к-рых осно­ван на вычислении термодинамич. характеристик, а также спектра коле­баний кристаллической решётки для разл. модификаций.

Структура крист. решётки при Т=0К определяется минимумом внутр. энергии Н система ч-ц. При T>0 К структура определяется минимумом

свободной энергии U куда, кроме H, входит т. н. энтропийный член SТ, связанный с тепловыми колебаниями атомов (U=H-TS, где S — энтро­пия). Кривая для устойчивой низко­температурной -фазы U_(T) имеет вид, показанный на рис. Любой др. способ упаковки тех же атомов в кри­сталле (-фаза) имеет при Т=0 К



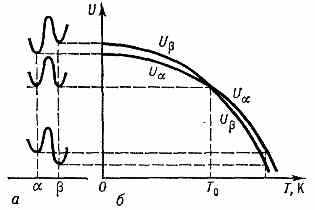
а — Изменение свободной энергии U кристал­ла при изменении взаимного расположе­ния атомов; минимумы соответствуют двум устойчивым полиморфным крист. модифика­циям  и ; б — зависимость U от темп-ры.


U_>U_. Это означает, что -фаза не­устойчива при низких темп-pax. Одна­ко из-за иного характера тепловых колебаний атомов кривая U_(T) идёт более полого, в точке Т₀ она пересе­кается с кривой U_ и далее идёт ниже. Это означает, что при Т<Т₀ устойчива -фаза, при Т>Т₀ устойчива -фаза и точка Т₀ явл. точкой равновесия фаз.

Переход менее стабильной модифи­кации в более стабильную связан с преодолением энергетич. барьера, к-рый существенно меньше, если пре­вращение происходит постепенно, пу­тём зарождения и последоват. роста в ней областей новой фазы. Барьер пре­одолевается за счёт тепловых флукту­ации; поэтому, если вероятность флук­туации мала, менее устойчивая фаза может длит. время существовать в метастабильном состоянии. Напр., ал­маз, области существования к-рого соответствуют T>1500 К и давление р=10⁸ Па, тем не менее может сущест­вовать неограниченно долго при атм. давлении и комнатной темп-ре, не превращаясь в стабильный при этих условиях графит. В др. веществах, наоборот, разл. модификации легко пе­реходят друг в друга при изменении темп-ры и др.

Полиморфные превращения могут сопровождаться изменением характера хим. связи и св-в. Напр., при высоких давлениях в нек-рых полупроводниках (Ge и Si) перекрытие и перестройка внеш. электронных оболочек атомов приводит к металлич. модификации. При давлении 2•10¹¹ Па возможно возникновение металлич. водорода при 5•10¹⁰ Па — металлич. Аг, Хе.

Частный случай П.— политипизм, к-рый наблюдается в нек-рых кристаллах со слоистой структурой (глинистые минералы кремния, карбид

561


кремния и др.}. Политипные модифи­кации построены из одинаковых слоев или слоистых «пакетов» атомов и раз­личаются способом и периодичностью наложения таких пакетов.

• Верма А., Кришна П., Полимор­физм и политипизм в кристаллах, пер. с англ., М., 1969; Кристиан Дж. Тео­рия превращений в металлах и сплавах, пер. с англ., т. 1, М., 1978; Уманский Я. С., С к а к о в Ю. А., Физика металлов, М., 1978.

А. Л. Ройтбурд.