П падение тела
| Вид материала | Документы |
- Тема «кинематика материальной точки», 29.33kb.
- Урок изучения новых знаний в 9-м классе по теме: "Свободное падение тел", 145.66kb.
- Программа вступительных испытаний по физике механика, 48.4kb.
- Тема: строение тела животных, 47.92kb.
- Конспект урока физики в 7 классе Тема : Вес тела, 40.5kb.
- Тема. Малые тела Солнечной системы, 383.39kb.
- Книга о душе, 521.77kb.
- Владимир Данченко принципиальные вопросы общей теории чакр и тантрическая концепция, 1664.57kb.
- Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 76.9kb.
- Беседа – лекция. Прием наркотика – всегда полет, но в конце – всегда падение, 83.01kb.
возможности создания конструкций миним. веса. В ряде совр. конструкций П. обеспечивает их наиболее рациональное функционирование, надёжность и безопасность, повышает сопротивляемость тел ударным нагрузкам, снижает концентрацию напряжений.
При растяжении цилиндрич. образца обнаруживают предел текучести s; при напряжениях s деформация обратима (упруга) и связана с Гука законом =Е (Е — модуль Юнга). При дальнейшем увеличении растягивающей силы зависимость ~ становится нелинейной и необратимой (рис.). Возрастание а с увеличением 8 наз. упрочнением. При разгрузке от напряжения >s (точка М) зависимость ~ изображается прибл.
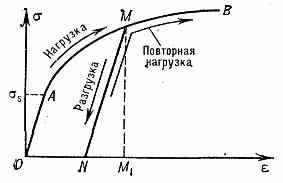
прямолинейным отрезком MN, параллельным нач. участку упругости ОА. Часть деформации e=NM1=/Е — упругая (обратимая). Отрезок p=ON — остаточная, или п л а с т и ч е с к а я, деформация, к-рая неизменна при разгрузке и возрастает при непрерывном нагружении ОАВ и при повторной нагрузке после достижения напряжения а, с к-рого была произведена разгрузка (рис.). В сложном напряжённом состоянии пластич. деформация появляется впервые при интенсивности напряжений us (условие П. Г е н к и — М и з е с а) или когда наибольшее касат. напряжение mas (где s — предел текучести при сдвиге) — условие П. Треска — Сен-Венана. При этом тензор деформации (см.
Деформация механическая) ij=eij+epij, где тензор упругой деформации eij связан с напряжениями обобщённым законом Гука, а тензор пластич. деформации pij характеризует деформацию, к-рая сохраняется в окрестности рассматриваемой точки, когда все компоненты тензора напряжений ij при разгрузке обращаются в нуль. Типичной явл. неоднозначность зависимости между напряжениями и упругопластич. деформациями: значения напряжений зависят не от текущих (мгновенных) значений деформации, а от того, в какой последовательности шло их изменение до достижения текущих значений, т. е. от процесса деформации.
• Ильюшин А. А., Пластичность, ч. 1, М.—Л., 1948.
В. С. Ленский.
547
ПЛАСТИЧНОСТЬ КРИСТАЛЛОВ, свойство крист. тел необратимо изменять свои размеры и форму под действием механич. нагрузок. Пластичность крист. тел (или материалов) связана с действием разл. микроскопич. механизмов пластич. деформации, относит. роль .каждого из к-рых определяется внеш. условиями: темп-рой, нагрузкой, скоростью деформирования. Эти механизмы рассмотрены ниже в порядке увеличения числа атомов, участвующих в элем. акте пластич. деформации.
С а м о д и ф ф у з и о н н а я и д и ф ф у з и о н н а я П. к. Перенос массы может осуществляться посредством самодиффузии по поверхности или через объём кристалла. Самодиффузия происходит путём проникновения атомов поверхностных слоев внутрь кристалла в виде междоузельных атомов на участках сжатия и «выделения» их на участках, подверженных действию растягивающих сил. Одновременно в противоположном направлении идёт поток вакансий, рождающийся в окрестности приложения растягивающих сил и аннигилирующих в местах действия сил сжатия на поверхности кристалла. В большинстве реальных случаев самодиффузионная деформация в осн. связана с направленными потоками вакансий, к-рые образуются легче, чем междоузельные атомы.
В кристалле, состоящем из атомов разного сорта, в однородном поле напряжений происходит ориентац. упорядочение относит. расположения атомов (рис., а), в результате чего кристалл приобретает нек-рую зависящую от степени упорядоченности деформацию.
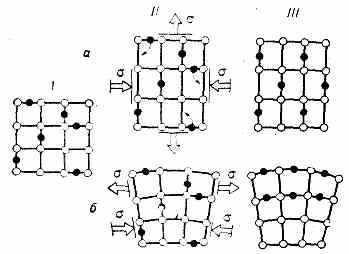
Диффузионная пластичность: а — ориентационное упорядочение примесных атомов (чёрные кружки) при сжатии — растяжении; б — перераспределение примесных атомов при изгибе; I — исходный кристалл; II -кристалл с примесными атомами под действием напряжений; 111 — конечная деформация кристалла.
После снятия напряжений упорядоченное состояние может быть невыгодно, но оно нек-рое время сохраняется. Если в кристалле создано неоднородное поле напряжений, то атомы примеси большего радиуса и междоузельные атомы (рис., б) стремятся перейти в растянутые области решётки, а меньшего — в сжатые; возникает неоднородное распределение концентраций, стабилизирующее исходную неоднородную деформацию. В реальных условиях перемещение дефектов происходит за счёт тепловых флуктуации, частота к-рых быстро падает с понижением темп-ры.
К р а у д и о н н а я П. к. обусловлена рождением и перемещением краудионов — сгущений атомов вдоль плотно упакованных рядов атомов в кристалле (см. Дефекты). При вдавливании острия в поверхность кристалла материал из зоны вдавливания удаляется «разбегающимися» из-под острия краудионами.
Д и с л о к а ц и о н н а я П. к. Типичный вид пластич. деформации кристаллов — скольжение по кристаллографич. плоскостям. Наиболее легко скольжение происходит по плотноупакованным плоскостям вдоль плотно-упакованных направлений. Скольжение по системе параллельных плоскостей даёт макроскопич. сдвиг, а сочетание сдвигов, соответствующих скольжению по разл. системам, составляет осн. часть пластич. деформации кристаллов. В реальных кристаллах в процессе их образования всегда возникают дислокации. Атомы вблизи дислокаций смещены из своих положений равновесия, а перевод их в новые положения равновесия, отвечающие сдвигу кристалла по плоскости скольжения на одно межатомное расстояние, требует значительно меньших затрат энергии, чем для атомов в неискажённом кристалле. Под действием напряжений дислокации способны увеличивать свою протяжённость (т. н. размножение дислокаций). Поэтому стадия образования новых дислокаций лишь в исключит. случаях лимитирует скольжение (напр., начало деформации в бездислокац. микрокристаллах). В остальных случаях развитие скольжения определяется движением дислокаций. По подвижности дислокаций все материалы делятся на 2 группы. В к о в а л е н т н ы х к р и с т а л л а х этот барьер для движения дислокаций по порядку величины приближается к энергии межатомных связей и может быть прёодолён только за счёт тепловой активации (термич. флуктуации). Поэтому подвижность дислокаций становится заметной лишь при достаточно больших темп-pax, а при умеренных — ковалентные кристаллы непластичны. В м е т а л л и ч е с к и х и и о н н ы х к р и с т а л л а х барьер для перемещения дислокаций в 103—104 раз меньше энергии связи и исчезает при напряжениях 10-3—10-4 G (где G — модуль сдвига); при таких напряжениях движение дислокаций не нуждается в тепловой активации и их подвижность слабо зависит от темп-ры. Поэтому сопротивление движению дислокаций пренебрежимо мало, чем обусловлена высокая пластичность ионных и металлич. кристаллов.
В р е а л ь н ы х к р и с т а л л а х имеются разл. дефекты (точечные дефекты, примесные атомы, дислокации, частицы др. фаз), и сопротивление скольжению зависит от вз-ствия движущихся дислокаций с этими дефектами. В результате вз-ствия друг с другом дислокации тормозятся и останавливаются, поэтому для протекания деформации с постоянной скоростью необходимо непрерывное рождение новых дислокаций. Это приводит к постоянному увеличению плотности дислокаций в кристалле, к-рая достигает 1011—1012 см-2; соответственно растёт их взаимное сопротивление скольжению — происходит деформац. упрочнение, или наклёп кристалла.
При высоких темп-pax дислокац. механизм П. к. сочетается с диффузионным и самодиффузионным. В кристаллах с примесями релаксация напряжений у дислокаций или дислокац. скоплений может осуществляться в результате перераспределения примесных атомов. Вокруг дислокаций образуются примесные «атмосферы», и дислокац. П. к. падает (деформац. старение). Поэтому удаление примесей обычно повышает П. к. Процессы разрядки дислокац. плотности вследствие взаимной аннигиляции дислокаций протекают более интенсивно в условиях высокотемпературной деформации, деформационное упрочнение падает и деформация развивается при постоянной нагрузке (ползучесть).
Для нек-рых кристаллов (напр., кварца, кальцита) преобладающим механизмом пластичности явл. двойникование. Необратимое изменение формы может быть также результатом образования под нагрузкой новой фазы, имеющей иную крист. решётку, чем исходный кристалл.
В п о л и к р и с т а л л а х действие рассмотренных механизмов пластич. деформации внутри зёрен осложнено вз-ствием между зёрнами. Деформация поликристалла есть суммарный результат деформации во многих различно ориентированных относительно нагрузок и находящихся в разл. условиях зёрен. Поэтому развитие деформации не имеет чётко выраженного стадийного характера, как деформации монокристаллов. Межзёренные границы препятствуют распространению дислокаций и, как правило, упрочняют крист. тела при низких темп-pax. Наоборот, при высоких темп-рах наличие границ, являющихся источниками или стоками дефектов, повышает П. к. Сочетание дислокац. и самодиффузионной деформаций в приграничных областях приводит к их высокой пластичности, проявляющейся в специфич. механизме высокотемпературной деформации поликристаллов — «проскальзывании» по границам зёрен. Перемещение зёрен друг относительно друга происходит подобно движению ч-ц в сыпучих материалах и в нек-рых случаях обеспечивает деформацию до 1000% («сверх-
548
пластичность»). Высокая П. к. может достигаться также, если в ходе деформирования успевает проходить рекристаллизация, приводящая к удалению наиболее искажённых и, следовательно, наименее пластичных зёрен, к-рые поглощаются растущими зёрнами с более совершенной структурой.
• Физика деформационного упрочнения монокристаллов, К., 1972; Набарро Ф. Р., Б а з и н с к и й 3. С., X о л т Д. Б., Пластичность чистых монокристаллов, пер. с англ., М., 1967; Хоникомб Р., Пластическая деформация металлов, пер. с англ., М., 1972; Современная кристаллография, т. 4, М., 1981. А. Л. Ройтбурд.
«ПЛЕНЕНИЕ ЦВЕТА», удержание «цветных» кварков и глюонов внутри адронов. См. Удержание «цвета».
ПЛЕОХРОИЗМ (от греч. pleon — более многочисленный, более протяжённый и chroa — цвет), изменение окраски в-ва в проходящем свете в зависимости от направления распространения и поляризации этого света. Впервые наблюдался в 1809 франц. учёным П. Л. А. Кордье, а затем (на кристаллах турмалина) в 1816 франц. физиком Ж. Б. Б и о и нем. физиком Т. И. Зеебеком. П.—одно из проявлений оптической анизотропии. П. обусловлен анизотропией поглощения, к-рое, в свою очередь, зависит от длины волны и поляризации излучения. Чаще всего П. наблюдается в кристаллах. У одноосных кристаллов различают 2 «главные» (основные) окраски — при наблюдении вдоль оптич. оси и перпендикулярно к ней; у двуосных кристаллов — 3 осн. окраски — при наблюдении по 3 направлениям, к-рые обычно совпадают с г л а в н ы м и н а п р а в л е н и я м и кристалла (см. Кристаллооптика). По др. направлениям кристалл виден окрашенным в иные, т. н. промежуточные, цвета. Сильным П. отличаются, напр., турмалин (одноосный кристалл) и ацетат меди (двуосный кристалл). Разновидностями П. явл. к р у г о в о й д и х р о и з м (Коттона эффект) — различие поглощения для света правой и левой круговых поляризаций, и л и н е й н ы й д и х р о и з м — неодинаковость поглощения обыкновенного и необыкновенного лучей. Анизотропией поглощения, кроме кристаллов, могут обладать и отд. молекулы; преимуществ. ориентация таких молекул вызывает П. содержащих их в-в (напр., мн. красителей). Преимуществ. ориентация анизотропно поглощающих молекул, ведущая к П., может быть естественной и искусственной — вызванной внеш. полем или механич. деформациями. Очень важным практич. применением П. явл. использование поляроидов, действие к-рых основано на явлении линейного дихроизма.
• Белянкин Д. С., Петров В. П., Кристаллооптика, 4 изд., М., 1951; К о с т о в И., Кристаллография, пер. с болг., М., 1965. См. также лит. при ст. Кристаллоптика.
ПЛЕЧО СИЛЫ, кратчайшее расстояние от данной точки (центра) до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы (см. Момент силы).
ПЛОСКАЯ ВОЛНА, волна, у к-рой направление распространения одинаково во всех точках пространства. Простейший пример — однородная монохроматич. незатухающая П. в.:
и(z, t)=Aeit±ikz, (1)
где А — амплитуда, = t±kz — фаза, =2/Т — круговая частота, Т -период колебаний, k — волновое число. Поверхности постоянной фазы (фазовые фронты) =const П. в. являются плоскостями.
При отсутствии дисперсии, когда фазовая скорость vф и групповая скорость vгр одинаковы и постоянны (vгр=vф= v), существуют стационарные (т. е. перемещающиеся как целое) бегущие П. в., к-рые допускают общее представление вида:
u(z, t)=f(z±vt), (2)
где f — произвольная функция. В нелинейных средах с дисперсией также возможны стационарные бегущие П. в. типа (2), но их форма уже не произвольна, а зависит как от параметров системы, так и от характера движения волны. В поглощающих (диссипативных) средах П. в. уменьшают свою амплитуду по мере распространения; при линейном затухании это может быть учтено путём замены в (1) k на комплексное волновое число kд ± ikм, где kм — коэфф. затухания П. в.
Однородная П. в., занимающая всё бесконечное пространство, является идеализацией, однако любое волновое поле, сосредоточенное в конечной области (напр., направляемое линиями передачи или волноводами), можно представить как суперпозицию П. в. с тем или иным пространств. спектром k. При этом волна может по-прежнему иметь плоский фазовый фронт, но неоднородное распределение амплитуды. Такие П. в. наз. плоскими неоднородными волнами. Отдельные участки сферич. и цилиндрич. волн, малые по сравнению с радиусом кривизны фазового фронта, приближённо ведут себя как П. в.
• См. лит. при ст. Волны.
М. А. Миллер, Л. А. Островский.
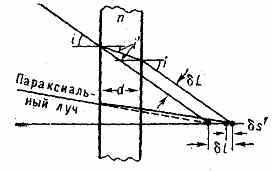
ПЛОСКОПАРАЛЛЕЛЬНАЯ ПЛАСТИНКА, слой однородной прозрачной среды с показателем преломления n, ограниченный параллельными плоскостями на расстоянии d друг от друга. Оптич. толщина П. п. равна nd, оптическая сила — нулю, увеличение оптическое — единице. П. п., поставленная на пути гомоцентрического пучка лучей, смещает (вдоль оси пучка) изображение, даваемое этим пучком, на расстояние l=d(1-tgi'/tgi) (рис.), где i — угол падения пучка лучей, a i' — угол преломления. В случае параксиальных пучков лучей l= d(1-1/n) П. п. сохраняет направление падающего на неё параллельного пучка лучей, но смещает ось этого пучка на величину L=lsini.
П. п. как оптич. элемент обладает аберрациями (см. Аберрации оптических систем), в частности сферической аберрацией (к-рая при больших углах i даёт дополнит. смещение s'), хроматической аберрацией и астигматизмом (для достаточно удалённых объектов и малых d — незначительными).
П. п. применяют как защитные стёкла, для окон, светофильтров (П. п. из окрашенных материалов), в угломерных приборах для малых угловых смещений изображения, в нек-рых интерферометрах (см. Люммера — Герке пластинка, Майкельсона эшелон], в качестве оптич. компенсаторов и т. д.
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ (плоское движение) твёрдого тела, движение тв. тела, при к-ром все его точки перемещаются параллельно нек-рой неподвижной плоскости. Изучение П. д. сводится к изучению движения неизменяемой плоской фигуры в её плоскости, к-рое слагается из поступательного движения вместе с нек-рым произвольно выбранным полюсом и вращательного движения вокруг этого полюса. П. д. можно также представить как серию элем. поворотов вокруг непрерывно меняющих своё положение мгновенных центров вращения.
ПЛОСКОПАРАЛЛЕЛЬНОЕ ТЕЧЕНИЕ, движение жидкости или газа параллельно к.-л. плоскости, при к-ром во всех точках, находящихся на одном перпендикуляре к этой плоскости, скорости ч-ц, давление и др. хар-ки потока одинаковы. Примеры П. т.: обтекание крыла бесконечно большого размаха потоком, перпендикулярным размаху, водослив через прямую плотину бесконечно большой ширины и др. Исследование П. т. значительно проще, чем исследование пространств. потока, т. к. все величины, характеризующие движение, не зависят от координаты, перпендикулярной к плоскости движения. При решении конкретных технич. задач в результаты, даваемые теорией П. т., вносятся соответствующие поправки (см., напр., Индуктивное сопротивление).
ПЛОСКОСТЬ ПОЛЯРИЗАЦИИ, плоскость, проходящая через направление колебаний электрич. вектора линейно поляризованной световой волны (см. Поляризация света) и направление распространения этой волны.
ПЛОТНОМЕР, прибор для измерения плотности в-в. Наиб. распространены
549
П. для измерения плотности жидкостей; они делятся на поплавковые, весовые, гидростатические, радиоизотопные, вибрационные, ультразвуковые. К П. примыкают приборы для измерения концентрации р-ров (спиртомеры, сахаромеры, нефтеденсиметры и др.). П о п л а в к о в ы е П. представляют собой ареометры пост. массы или пост. объёма. В е с о в ы е П. основаны на непрерывном взвешивании определённого объёма жидкости. В г и д р о с т а т и ч е с к и х П. плотность определяют по разности давлений двух столбов жидкости разной высоты. Действие р а д и о и з о т о п н ы х П. основано на измерении ослабления пучка - или -лучей в результате их поглощения или рассеяния слоем жидкости. В в и б р а ц и о н н о м П. используется зависимость резонансной частоты возбуждаемых в жидкости колебаний от её плотности, в ультразвуковом — зависимость скорости звука в среде от её плотности. Радиоизотопный, ультразвуковой, вибрационный и др. методы могут быть применены для определения плотности тв. и газообразных в-в.
•-Кивилис С. Ш., Приборы для измерения плотности жидкостей и газов, в кн.: Приборостроение и средства автоматики, т. 2, кн. 2, М., 1964; Измерение массы, объема и плотности, М., 1972; Глыбин И. П., Автоматические плотномеры, К., 1965.
С. Ш. Кивилис.
ПЛОТНОСТЬ (), величина, определяемая для однородного в-ва его массой в единице объёма. П. неоднородного в-ва в определённой точке — предел отношения массы т тела к его объёму V, когда объём стягивается к этой точке. Средняя П. неоднородного тела также есть отношение m/V. Часто применяется понятие о т н о с и т е л ь н о й П.; напр., П. жидких и тв. в-в может определяться по отношению к П. дистиллированной воды при 4°С, а газов — по отношению к П. сухого воздуха или водорода при нормальных условиях. Единица П. в СИ — кг/м3, в системе СГС — г/см3. П. и уд. вес связаны между собой отношением =ag, где g — местное ускорение свободного падения тела, а — коэфф. пропорциональности, зависящий от выбора единиц измерения. П. в-в, как правило, уменьшается с ростом темп-ры и увеличивается с повышением давления (П. воды с понижением темп-ры Т до 4°С растёт, при дальнейшем понижении Т — уменьшается). При переходах в-ва из одного агрегатного состояния в другое П. изменяется скачкообразно: резко увеличивается при переходе в газообразное состояние и, как правило, уменьшается при затвердевании (П. воды и чугуна аномально уменьшается при переходе из жидкой фазы в твёрдую). Методы измерения П. в-в весьма разнообразны. II. идеальных газов определяется из ур-ния состояния: =p/RT, где р — давление, — мол. масса, R — универсальная газовая постоянная, Т — абс. темп-pa. П. сухого газа, имеющего при нормальных условиях П. н, при давлении р и темп-ре Т определяется ф-лой: =нрТн/рнТК, где К — коэфф. сжимаемости, характеризующий отклонение данного реального газа от идеального. Для влажного газа =н(р-pв)Тн/рнТК+в>, где — относит. влажность газа, рв и в табличные значения максимально возможного давления при темп-ре Т и максимально возможной П. водяного пара при данных р и Т. П. жидкостей и тв. тел находят путём точного определения массы тела и его объёма с помощью разл. типов плотномеров. Для определения П. используют также зависимость П. от скорости распространения звуковых волн, интенсивности - и -излучения, прошедшего через в-во, и т. д.
• ГОСТ 2939—63. Газы. Условия для определения объема, М., 1965; Измерение массы объема и плотности, М., 1972.
