Вопросы к экзамену по математическому анализу (зимняя сессия)
| Вид материала | Вопросы к экзамену |
- Вопросы к экзамену по математическому анализу для студентов, обучающихся по специальности, 25.22kb.
- Вопросы к экзамену по математическому анализу для 1 курса д/о, 33.33kb.
- Вопросы к экзамену по математическому анализу для студентов 1-го курса специальности, 25.55kb.
- Вопросы к экзамену по общей психологии 2-й курс, д/о, 2011-2012 уч г., зимняя сессия, 24.94kb.
- Вопросы к экзамену по математическому анализу, 26.87kb.
- Экзаменационные вопросы по математическому анализу для студентов 1 курса 6 факультета, 33.76kb.
- Экзаменационные вопросы по математическому анализу для студентов i-го курса 6 факультета, 27.4kb.
- Лекций: 18 Практических: 16 Лабораторных: 0 end. 9 Модели плоскости Лобачевского ects:, 15.95kb.
- Лекций: 34 Практических: 18 Лабораторных: 0 taс. 9 Теория автоматического управления, 21.9kb.
- Программа по математическому анализу, 15.51kb.
ВОПРОСЫ
к экзамену по математическому анализу (зимняя сессия)
1 курс 1 семестр РТФ
Преподаватель Коломиец Л.В.
2008-2009 учебный год
- Множества, операции над множествами. Примеры множеств. Метод математической индукции.
- Понятие функции. Способы задания функций. Примеры. Элементарные функции, гиперболические функции. Обратные, неявные, параметрически заданные функции. Циклоида, астроида.
- Декартовы и полярные координаты на плоскости. Примеры кривых в полярных координатах.
- Определение числовой последовательности. Определение монотонной, ограниченной, неограниченной последовательности. Определение последовательности, ограниченной сверху, ограниченной снизу. Теорема о свойстве верхней грани.
- Два определения предела числовой последовательности. Примеры.
- Свойства сходящихся последовательностей (единственность предела, ограниченность).
- Теорема об арифметических операциях со сходящимися последовательностями.
- Теоремы о продельном переходе в неравенствах.
- Бесконечно большие и бесконечно малые последовательности. Теорема об их связи.
- Теоремы о произведении ограниченной последовательности на бесконечно малую и о связи членов последовательности со своим пределом.
- Признаки сходимости монотонных последовательностей (три теоремы Вейерштрасса).
- По признаку Вейерштрасса доказать, что последовательность
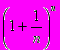 имеет предел.
имеет предел.
- Определения предела функции по Гейне и по Коши. Геометрическая интерпретация. Эквивалентность определений предела функции по Гейне и по Коши.
- Односторонние пределы. Теорема о существовании предела в точке.
- Свойства функций, имеющих конечный предел.
- Бесконечно малые и бесконечно большие функции. Теоремы об их связи, о связи функции со своим пределом. Свойства бесконечно малых функций.
- Первый замечательный предел. Следствия.
- Второй замечательный предел. Следствия.
- Сравнение бесконечно малых. Примеры.
- Свойства эквивалентных бесконечно малых.
- Определения функции, непрерывной в точке. Их эквивалентность. Примеры. Непрерывность элементарных функций и доказательство для
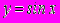 .
.
- Локальные свойства функций, непрерывных в точке.
- Первая теорема Больцано - Коши о функции, имеющей на концах отрезка значения разных знаков.
- Вторая теорема Больцано - Коши о прохождении непрерывной функции через любое промежуточное значение.
- Первая теорема Вейерштрасса об ограниченности функции, непрерывной на отрезке.
- Вторая теорема Вейерштрасса о достижении функцией, непрерывной нà отрезке, наибольшего и наименьшего значений.
- Определение производной функции в точке. Односторонние производные. Примеры функций, не имеющих производной в точке.
- Физический и геометрический смысл производной. Уравнение касательной и нормали к кривой.
- Определение дифференцируемости функции в точке. Теоремы о связи дифференцируемости и существовании конечной производной, дифференцируемости и непрерывности.
- Формулы производных произведения и частного функций.
- Теоремы о производных обратной и сложной функций.
- Определение дифференциала, его геометрический смысл. Теорема об эквивалентности дифференциала и приращения функции, ее применение к приближенным вычислениям.
- Определение производных и дифференциалов высших порядков. Примеры. Формула Лейбница. Производные высших порядков от функций, заданных параметрически.
- Теорема Ферма о дифференцируемой функции.
- Теорема Ролля и ее геометрический смысл.
- Теорема Лагранжа о конечных приращениях и ее геометрический смысл.
- Теорема Коши о конечных приращениях.
- Правило Лопиталя для неопределенностей
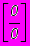 и
и  .
.
- Формула Тейлора с остаточным членом в форме Лагранжа и Пеано.
- Формулы Маклорена для функций
 .
.
- Теорема о необходимых и достаточных условиях возрастания и убывания функции.
- Необходимое условие существования экстремума. Достаточные признаки экстремума.
- Определение выпуклой и вогнутой функции. Достаточный признак выпуклости и вогнутости.
- Определение точки перегиба. Необходимый признак точки перегиба. Достаточные признаки точки перегиба.
- Определение вертикальной, горизонтальной и наклонной асимптот графика функции. Правило вычисления наклонной асимптоты.
ЗАДАЧИ
к экзамену по математическому анализу
- Доказать, что
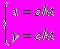 - параметрическое уравнение гиперболы и построить гиперболу.
- параметрическое уравнение гиперболы и построить гиперболу.
- Найти область определения и построить лемнискату Бернулли:
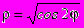 . Записать эту кривую в декартовых координатах.
. Записать эту кривую в декартовых координатах.
- Доказать, что последовательность
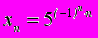 не ограничена. Является ли она бесконечно большой?
не ограничена. Является ли она бесконечно большой?
- Записать на языке
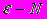 следующее выражение:
следующее выражение: 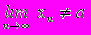 .
.
- Доказать, что последовательность
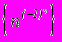 не имеет предела.
не имеет предела.
- Доказать методом математической индукции неравенство Бернулли:
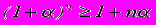 .
.
- Доказать методом математической индукции формулу:
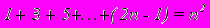 .
.
- Верно ли утверждение: если
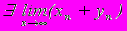 , то
, то 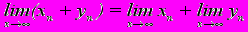 ?
?
- Верно ли утверждение: если
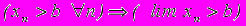 ?
?
- Сформулировать и доказать теорему о свойстве нижней грани.
- Доказать по определению, что
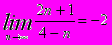 .
.
- Какие из утверждений неверны и почему:
а) если немонотонная последовательность сходится, то она ограничена;
б) если последовательность сходится, то она ограничена и монотонна;
в) если немонотонная последовательность ограничена сверху и снизу, то она сходится.
- Доказать, что предел функции
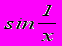 при
при  не существует.
не существует.
- Доказать, что предел функции
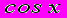 при
при  не существует.
не существует.
- .Доказать по определению Коши, что
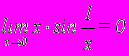 .
.
- Доказать по определению, что
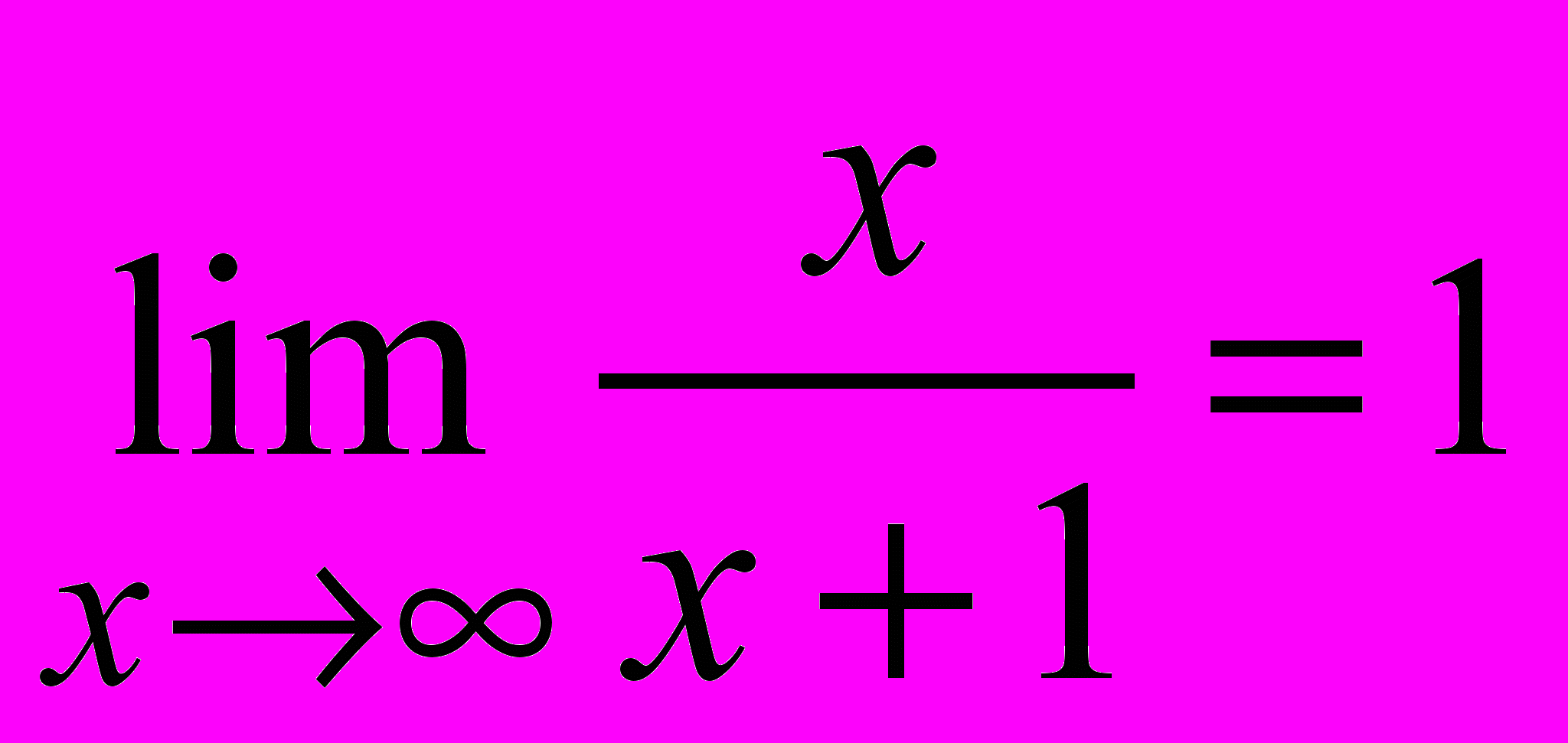 .
.
- Доказать по определению, что
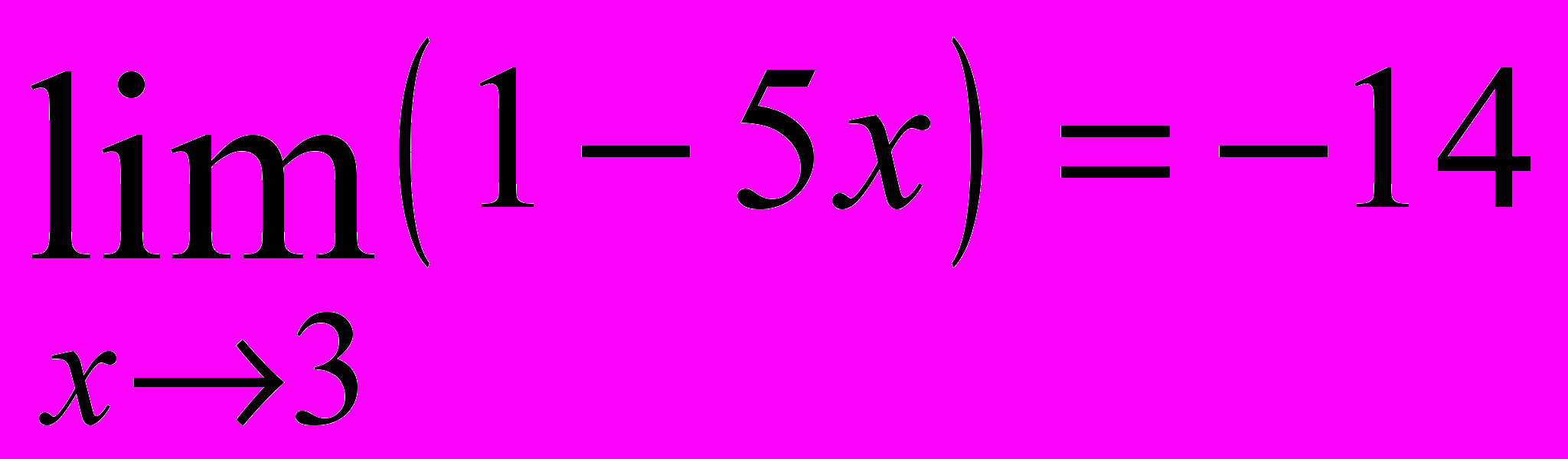
- Доказать на основании 2 замечательного предела следующие эквивалентности:
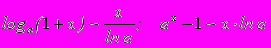 .
.
- Привести примеры функций, непрерывных в точке, но не дифференцируемых в этой точке:
а) функция непрерывна, производная не существует;
б) функция непрерывна, производная равна бесконечности.
- Найти с помощью определения производную функции
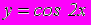 .
.
- Найти с помощью свойств производных производную функции
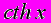 .
.
- Найти с помощью теоремы о производной обратной функции производную функции
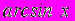 .
.
- Найти с помощью теоремы о производной обратной функции производную функции
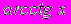 .
.
- Доказать с помощью логарифмического дифференцирования формулу производной функции
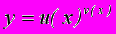 .
.
- Записать по формуле Маклорена разложение функций:
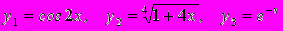 .
.
- Доказать с помощью правила Лопиталя, что показательная функции
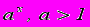 растет быстрее любой степенной
растет быстрее любой степенной 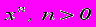 , а степенная, в свою очередь, быстрее любой логарифмической
, а степенная, в свою очередь, быстрее любой логарифмической 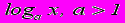 .
.
- Доказать с помощью правила Лопиталя, что
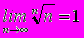 .
.
