Geum.ru

Вопросы к экзамену по математическому анализу для 1 курса д/о

Вид материалаВопросы к экзамену
Подобный материал:
Проф. Корешкова Т.А.


Вопросы к экзамену по математическому анализу для 1 курса д/о,

специальность математика.


  1. Множество действительных чисел, его основные свойства.
  2. Различные формулировки свойства непрерывности множества действительных чисел, их эквивалентность.
  3. Принцип разделяющего числа. Критерий единственности разделяющего числа.
  4. Рациональные и иррациональные числа. Числовая прямая, числовые промежутки, окрестности. Модуль числа и его свойства.
  5. Числовая функция и способы ее задания. График функции. Сужение функции.
  6. Свойства функций: четность, нечетность, периодичность, монотонность, ограниченность; особенности графиков.
  7. Числовая последовательность, способы ее задания. Предел последовательности: определение, геометрический смысл.
  8. Свойства сходящейся последовательности (теоремы о единственности предела и об ограниченности сходящейся последовательности).
  9. Теорема Вейерштрасса о сходимости монотонной ограниченной последовательности.
  10. Теорема о сходимости подпоследовательности, сходящейся к последовательности.
  11. Теорема о выделении из ограниченной последовательности сходящейся подпоследовательности.
  12. Теорема о стягивающейся последовательности вложенных отрезков.
  13. Число «е» как предел последовательности.
  14. Бесконечно малые функции при х 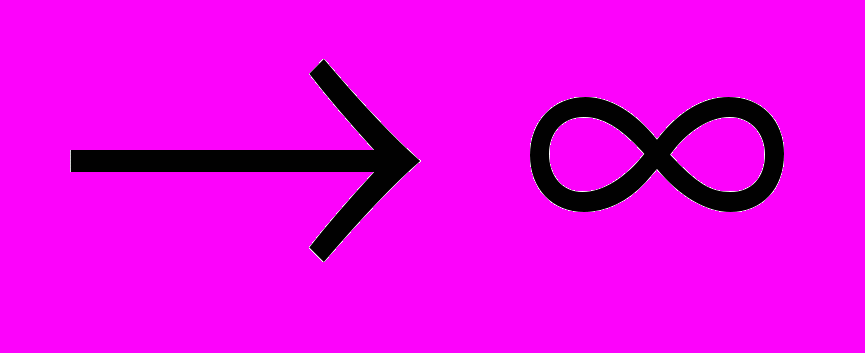и х: определение, геометрический смысл, свойства.
  15. Бесконечно большие функции при х 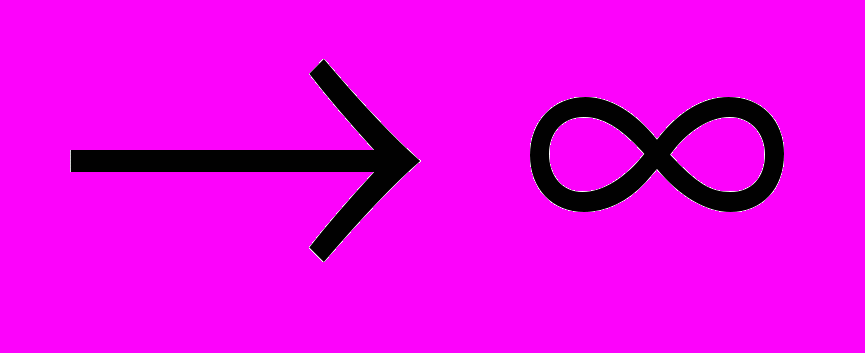и х: определение, геометрический смысл, свойства, связь с бесконечно малыми.
  16. Предел функции при : определение и геометрический смысл. Теорема о единственности предела.
  17. Предел функции при , различные формулировки и их эквивалентность. Односторонние пределы и их связь с пределом функции в точке.
  18. Теоремы о предельном переходе в неравенствах.
  19. Теорема о пределе промежуточной функции при , при .
  20. Теорема об ограниченности на луче функции, имеющей предел при .
  21. Теоремы о пределе суммы и произведения функций при , при .
  22. Теорема о пределе частного при и .
  23. Теорема о пределе отношения многочленов при .
  24. Отыскание асимптот графика функции. Горизонтальные, наклонные, вертикальные асимптоты.
  25. Различные определения непрерывности функции в точке, их эквивалентность. Непрерывность функции на промежутке.
  26. Определение непрерывности по Гейне, его эквивалентность определению непрерывности по Коши.
  27. Локальные свойства функции, непрерывной в точке: ограниченность и сохранение знака в окрестности точки.
  28. Необходимое и достаточное условия непрерывности функции в точке. Классификация точек разрыва.
  29. Арифметические операции над непрерывными функциями.
  30. Функция y = sinx: определение, свойства, график, непрерывность.
  31. Функция y = cosx: определение, свойства, график, непрерывность.
  32. Функции y = tgx, y = ctgx: определение, свойства, график, непрерывность.
  33. Функции y = arcsinx, y = arctgx: определение, свойства, график, непрерывность.
  34. Функции y = arccosx, y = arcctgx: определение, свойства, график, непрерывность.
  35. Композиция функции, непрерывность композиции. Переход к пределу под знаком непрерывной функции.
  36. Теорема о точках разрыва монотонной функции.
  37. Сравнение бесконечно малых. Эквивалентные бесконечно малые и их использование для вычисления пределов.
  38. Первый замечательный предел и связанные с ним эквивалентные бесконечно малые.
  39. Второй замечательный предел.
  40. Теорема о нулях непрерывной функции и ее использование для решения уравнений и неравенств.
  41. Теорема о промежуточном значении непрерывной функции.
  42. Необходимое и достаточное условие непрерывности монотонной функции.
  43. Теорема об ограниченности функции, непрерывной на отрезке.
  44. Теорема о достижении непрерывной функцией на отрезке своих наибольшего и наименьшего значений.
  45. Обратимая функция, обратная функция, график обратной функции. Теорема существования и непрерывности обратной функции.
  46. Существование арифметического корня. Степенная функция с рациональным показателем, ее непрерывность, графики (для различных значений показателя).
  47. Показательная функция на множестве рациональных чисел.
  48. Определение степени с иррациональным показателем.
  49. Показательная функция, ее свойства, график.
  50. Логарифмическая функция: определение, свойства, график.
  51. Гиперболические функции: определение, свойства, график.
  52. Пределы связанные с показательной и логарифмической функциями; соответствующие эквивалентные бесконечно малые.