Geum.ru

Экзаменационные вопросы по математическому анализу для студентов i-го курса 6 факультета (специалисты)

Вид материалаЭкзаменационные вопросы

Содержание


Раздел III.
Подобный материал:

Кафедра 803


Экзаменационные вопросы по математическому анализу

для студентов I-го курса 6 факультета (специалисты),

осенний семестр 2011/2012 учебного года.


Раздел 1. Последовательности. Функции. Теория пределов. Непрерывность функций одной переменной.

  1. Конечный предел числовой последовательности. Необходимое условие его существования. Формулировка критерия Коши сходимости числовой последовательности.
  2. Критерий сходимости монотонной последовательности.
  3. Бесконечно малые последовательности, их свойства. Бесконечно большие последовательности, их связь с бесконечно малыми.
  4. Теоремы о пределах суммы, произведения и частного сходящихся последовательностей.
  5. Теоремы о пределах последовательностей, связанных неравенствами.
  6. Число е, как предел последовательности с общим членом .
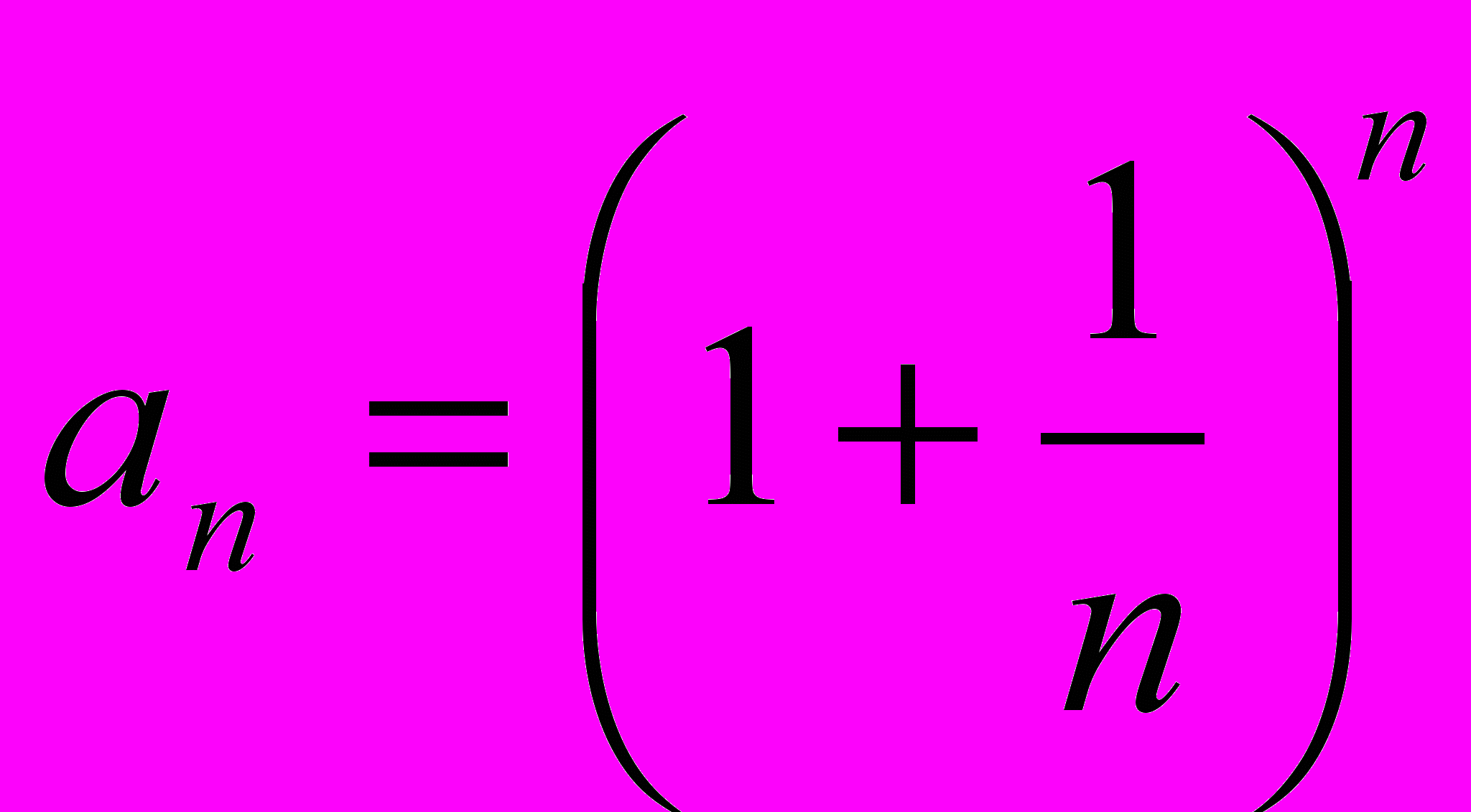  7. Конечный предел функции действительного переменного ( по Коши и по Гейне) при ха ( а - число или символ  ). Бесконечно большие функции при ха. Односторонние пределы.
  8. Основные теоремы о пределах функций (о пределе суммы, произведения и частного функций, о пределах функций, связанных неравенствами, о пределе сложной функции).
  9. Замечательные пределы.
  10. Сравнение функций. О и о символика. Эквивалентные бесконечно малые функции и их свойства.
  11. Функции действительного переменного, непрерывные в точке, их свойства. Непрерывность элементарных функций.
  12. Точки разрыва функции, их классификация.
  13. Непрерывность функции на интервале, на отрезке. Формулировка свойств функций, непрерывных на отрезке.


Раздел II. Дифференциальное исчисление функции одной переменной.

  1. Производная функции действительного переменного, её геометрический и механический смысл. Касательная и нормаль к кривой. Односторонние производные. Необходимые условия существования производной.
  2. Общие правила дифференцирования. Дифференцирование сложной функции, обратной функции.
  3. Производные элементарных функций. Логарифмическое дифференцирование.
  4. Дифференциал функции, его геометрический смысл, свойства, инвариантная форма записи, приложения.
  5. Производные и дифференциалы высших порядков, их свойства. Неинвариантность форма записи дифференциалов высших порядков.
  6. Функции , заданные параметрически, их дифференцирование.
  7. Теоремы Ферма, Ролля, их геометрический смысл.
  8. Теорема Лагранжа , её геометрический смысл. Теорема Коши.
  9. Правила Лопиталя.
  10. Формула Тейлора с остаточным членом в форме Пеано и Лагранжа. Формула Маклорена.
  11. Разложение по формуле Маклорена функций ex, sin x, cos x, ln (1+x), (1+х)n.
  12. Необходимые и достаточные условия монотонности функции. Экстремум функции, его необходимое условие, достаточные условия экстремума.
  13. Необходимые и достаточные условия выпуклости (вогнутости) графика функции. Необходимые и достаточные условия существования точки перегиба. Асимптоты графика функции.


Раздел III. Дифференциальное исчисление функции нескольких переменных. Предел. Непрерывность.

  1. Открытые и замкнутые множества в Rn, связные множества. Область, замкнутая область. Односвязные и многосвязные области.
  2. Функции нескольких переменных. Предел функции. Непрерывность функции в точке, области, замкнутой области. Формулировка свойств функций, непрерывных в ограниченных замкнутых областях.
  3. Частные производные и дифференцируемость функции нескольких переменных. Необходимые и достаточные условия дифференцируемости.
  4. Дифференциал функции нескольких переменных, его свойства.
  5. Производные сложных функций. Формула полной производной.
  6. Частные производные и дифференциалы высших порядков. Формула Тейлора.
  7. Экстремум функций нескольких переменных.
  8. Условный экстремум функции нескольких переменных.