Программа коллоквиума №1 по математическому анализу для студентов 1 курса экономического факультета ргу
| Вид материала | Программа |
СодержаниеОбразцы билетов Билет № 2 Билет № 3 Билет № 4 Программа коллоквиума № 2 по математическому анализу Образцы билетов Билет № 2 |
- Экзаменационные вопросы по математическому анализу для студентов 1 курса 6 факультета, 33.76kb.
- Экзаменационные вопросы по математическому анализу для студентов i-го курса 6 факультета, 27.4kb.
- Методические указания по организации и проведению преддипломной практики для студентов, 314.8kb.
- Вопросы к зачету по дисциплине математическое программирование для студентов 2 курса, 25.03kb.
- Планы семинарских занятий по курсу микроэкономика, часть 1 Для студентов 1 курса факультета, 124.35kb.
- Вопросы к экзамену по математическому анализу для студентов 1-го курса специальности, 25.55kb.
- Учебно-методический комплекс элективного курса «политико-правовой менеджмент» для студентов, 176.37kb.
- Бакалаврская программа № Кафедра региональной экономики и географии экономического, 143.68kb.
- Вопросы к экзамену по математическому анализу для студентов, обучающихся по специальности, 25.22kb.
- Вопросы к экзамену по математическому анализу для 1 курса д/о, 33.33kb.
ПРОГРАММА КОЛЛОКВИУМА № 1 ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
для студентов 1 курса экономического факультета РГУ
(специальность «Менеджмент организаций»»)
2004/2005 учебный год, 2-й семестр
1. Модуль вещественного числа, его свойства. Что представляют собой множества, описанные неравенствами: |x|<6; |x-3|>4; |x+2|=5; |x-4|2; |x|3 …
2. Окрестности числа и бесконечно удаленной точки (определения и примеры).
3. Функция одного переменного и ее график (определения). Построение графиков функций –f(x), f(-x), |f(x)| при известном графике f(x). Знать и уметь использовать свойства и графики элементарных функций.
4. Четность-нечетность функций (знать определения, свойства графиков; уметь проверить наличие одного из этих свойств).
5. Ограниченность функции (определения, примеры ограниченных и неограниченных функций). Уметь доказывать по определению ограниченность функций вида f(x)=x2/( x2+1); f(x)=cosx/(2+cos2x)
6. Числовая последовательность как функция. Предел числовой последовательности, сходимость.
7. Понятие о монотонной и ограниченной числовой последовательностях, теорема о пределе монотонной ограниченной последовательности. Число «e», функции «экспонента» и «натуральный логарифм».
8. Различные определения предела функции (общие и варианты для конкретных случаев).
9. Конечный предел функции (определение) и его единственность (с доказательством).
10. Теорема об ограниченности функции, имеющей конечный предел (доказывать). Подобрать пример функции, ограниченной, но не имеющей предела в окрестности какой-либо точки.
11. Теорема о переходе к пределу в неравенствах (формулировка). Найти limx0 f(x), если в окрестности x=0 выполняется неравенство sinx f(x) x/(x+1).
12. Бесконечно малые функции, их свойства (c доказательством). Уметь обоснованно (с учетом свойств) доказывать, что данная функция является бесконечно малой (например, для функций f(x)=sinx/(x+1) в окрестности x=0; f(x)=tg(x-1)+x-1 в окрестности x=1).
13. Бесконечно большие функции, их свойства. Уметь обоснованно (с учетом свойств) доказывать, что данная функция является бесконечно большой (например, для функций f(x)=cosx+x при x; f(x)=x+1/x при x).
14. Определения бесконечно малой и бесконечно большой функции, теорема о связи между ними (доказывать).
15. На примерах объяснить, почему отношение бесконечно малых функций является неопределенностью.
16. Бесконечно малые функции (определение), лемма о представлении функции, имеющей конечный предел (доказывать).
17. Теорема об арифметических действиях с пределами функций (доказывать утверждения для суммы и произведения).
18. Понятие о сложной функции, теорема о пределе сложной функции(формулировка).
19. Замечательные пределы, эквивалентные функции, теорема о замене эквивалентных функций, цепочки эквивалентностей.
20. Односторонние пределы (определения), теорема о связи с обычным пределом.
21. Функция знака, построение графиков функции sgnf(x).
22. Приращения аргумента и функции, определение непрерывности функции в точке и на множестве, критерий непрерывности функции (доказывать).
23. Теоремы о непрерывных функциях (формулировки).
24. Проверка непрерывности строчно заданных функций в точках «склейки».
Образцы билетов
Билет № 1
1. Конечный предел функции (определение) и его единственность (доказать).
2. Сформулируйте теоремы о непрерывных функциях. Является ли непрерывной на (-3;3) функция
f(x) = cosx / (x+5)?
3. Построить график функции f(x)=|x2 –6x-7|
Билет № 2
1. Конечный предел функции (определение). Теорема об ограниченности функции, имеющей конечный предел (доказать).
2. Бесконечно большие функции и их свойства. Докажите, что lim x (x2– cosx)=.
3. Проверьте наличие свойства четности-нечетности у функции f(x)=( 3x-1) / (3x+1).
Билет № 3
1. Определение бесконечно малой функции, лемма о представлении функции, имеющей конечный предел (доказать).
2. Дайте определение ограниченной функции, покажите ограниченность на множестве (-4;4) функции
f(x) = cosx(x-10).
3.Какие числовые интервалы представляют собой множества, описанные неравенствами |x+3| 5; |x| 4?
Билет № 4
1. Теорема об арифметических действиях с пределами (доказать утверждение о сумме).
2. Дать определение модуля вещественного числа, перечислить его свойства. Описать с помощью числовых неравенств и интервалами множество чисел, удовлетворяющих неравенству |x|100.
3. Проверить непрерывность в точке x = 1 функции
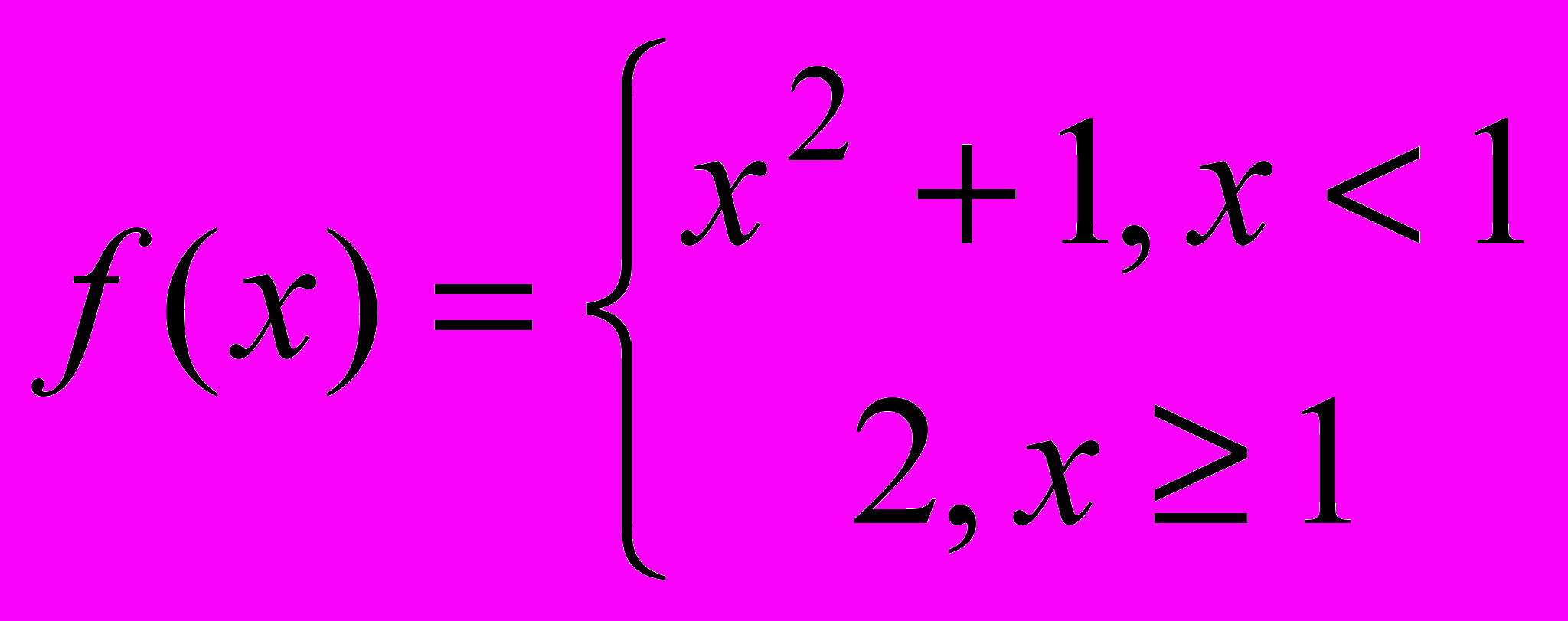
ПРОГРАММА КОЛЛОКВИУМА № 2 ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
для студентов 1 курса экономического факультета РГУ
(специальность «Менеджмент организаций»»)
2004/2005 учебный год, 2-й семестр
Знаком * выделены дополнительные вопросы, частично не рассмотренные на лекциях, но использующие материал этого и прошлого семестров, предлагаемые на оценку «5»
1. Определение непрерывности функции в точке, приращения аргумента и функции, критерий непрерывности функции в точке (доказать).
2. Приращения аргумента и функции, определение производной функции в точке, физический смысл производной.
3. Приращения аргумента и функции, определение производной функции в точке, геометрический смысл производной (доказать).
4 (*). Геометрический смысл производной функции в точке. Составить уравнение касательной, проходящей к графику заданной функции в указанной точке.
5 (*). Считая, что угол между линиями можно рассматривать как угол между касательными к их графикам, проведенными в точке пересечения линий, найти угол между заданными кривыми (например, между графиками функций
; 
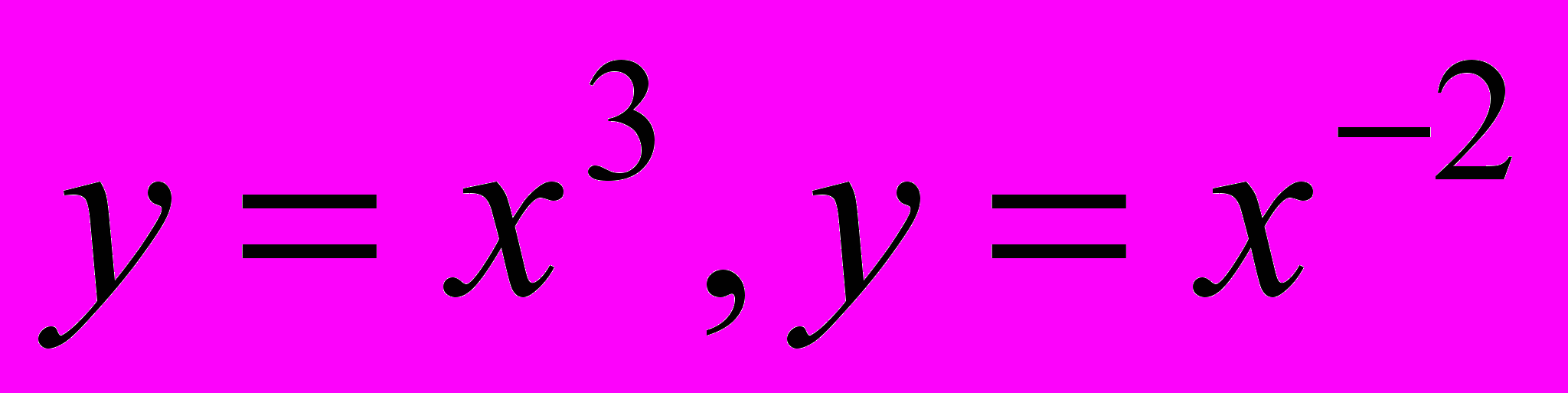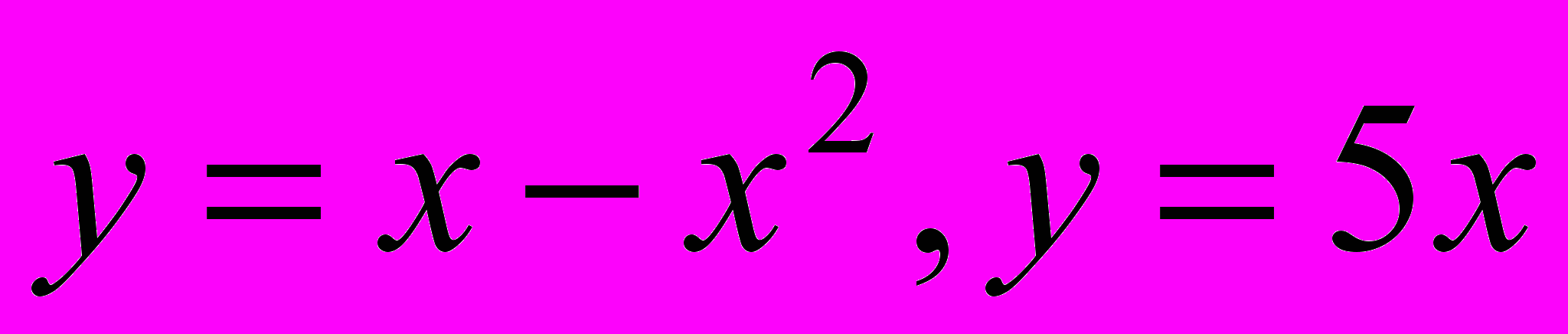),6. Приращения аргумента и функции, определение производной функции в точке, понятие о бесконечной производной и дифференцируемой функции.
7. Основные правила дифференцирования (теоремы о производной суммы, произведения, частного (*) – доказывать, производная сложной функции – только формулировка).
8. Приращения аргумента и функции, определение производной функции в точке, вывод производной функции y=sin x, y=cos x (*).
9. Основные правила дифференцирования, вывод производной функции y=tgx, y=ctgx (*).
10. Теорема о дифференцируемости (доказывать), определение дифференциала функции, формула для его вычисления.
11.Определение дифференциала функции, нахождение по определению дифференциала для y=x2, y=x3(*).
12. Правило Лопиталя (формулировка).
13. Теорема Лагранжа (с геометрической иллюстрацией).
14. Теорема Лагранжа (формулировка), два следствия (с доказательством).
15 (*). Определение возрастания (убывания) функции, критерий нестрогой монотонности (доказывать отдельно для случая убывания и возрастания), критерий строгой монотонности (формулировки).
16. Определения точек экстремума и экстремумов функции (локальных максимума и минимума).
17 (*). Необходимое условие экстремума (доказательство для случая точки максимума и точки минимума).
18. Формулировка первого достаточного условия точки экстремума.
19. Понятие об абсолютном экстремуме функции, теорема о наибольшем и наименьшем значениях функции на отрезке (формулировка).
20 (*). Наибольшее и наименьшее значение функции на интервале, прикладные задачи, например:
- Сыр реализуется по цене 150 р. за кг, x - объем выпуска сыра (в кг), функция издержек производства имеет вид S(x)=50x-3x3. Найти объем сыра, производство которого дает максимальную прибыль (и значение этой максимальной прибыли).
- Цена одной порции мороженого – х руб. Функция суточного спроса (объема продаж) в зависимости от цены имеет вид
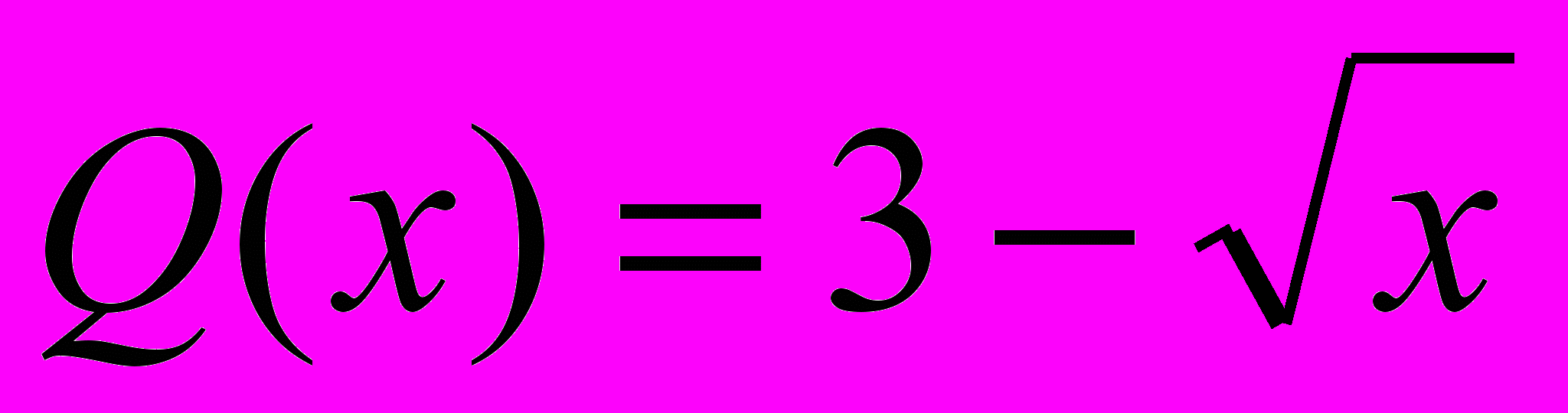(в сотнях порций). При какой цене за порцию выручка будет максимальной (найти значение этой выручки).
21. Понятие о направлениях выпуклости графика функции (для непрерывной и дифференцируемой функций).
22. Понятие о направлениях выпуклости графика для дифференцируемой функции, связь со знаком второй производной.
23. Определение точки перегиба графика функции, необходимое и достаточное условие (формулировки).
24. Второе достаточное условие экстремума, его применение на практике (например, используя второе достаточное условие, найти точки экстремума функций
, 
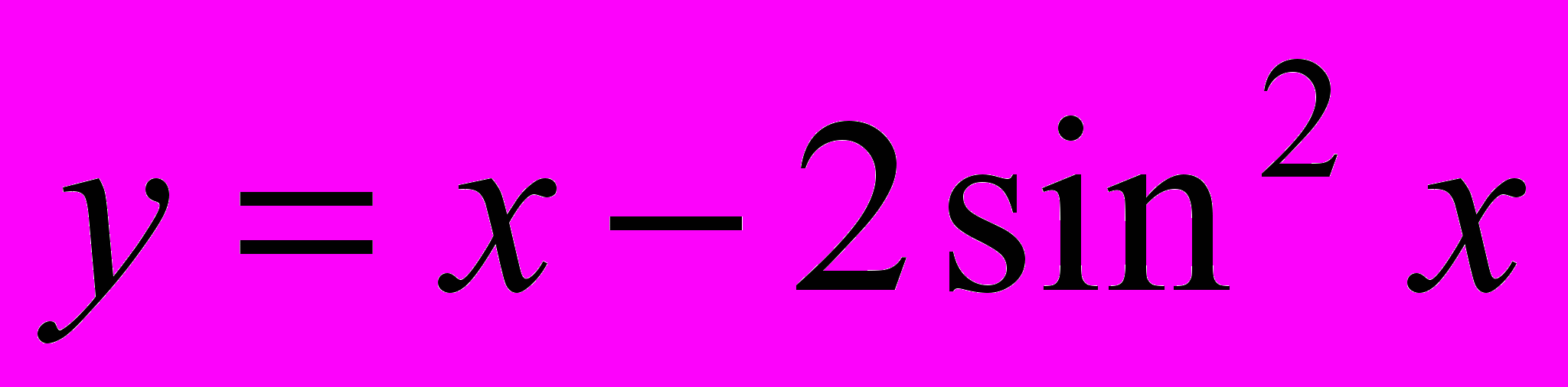).25. Вертикальные и наклонные асимптоты графика функции, определение и их нахождение (ПРИМЕРЫ: найти асимптоты графика функций
; 
; 
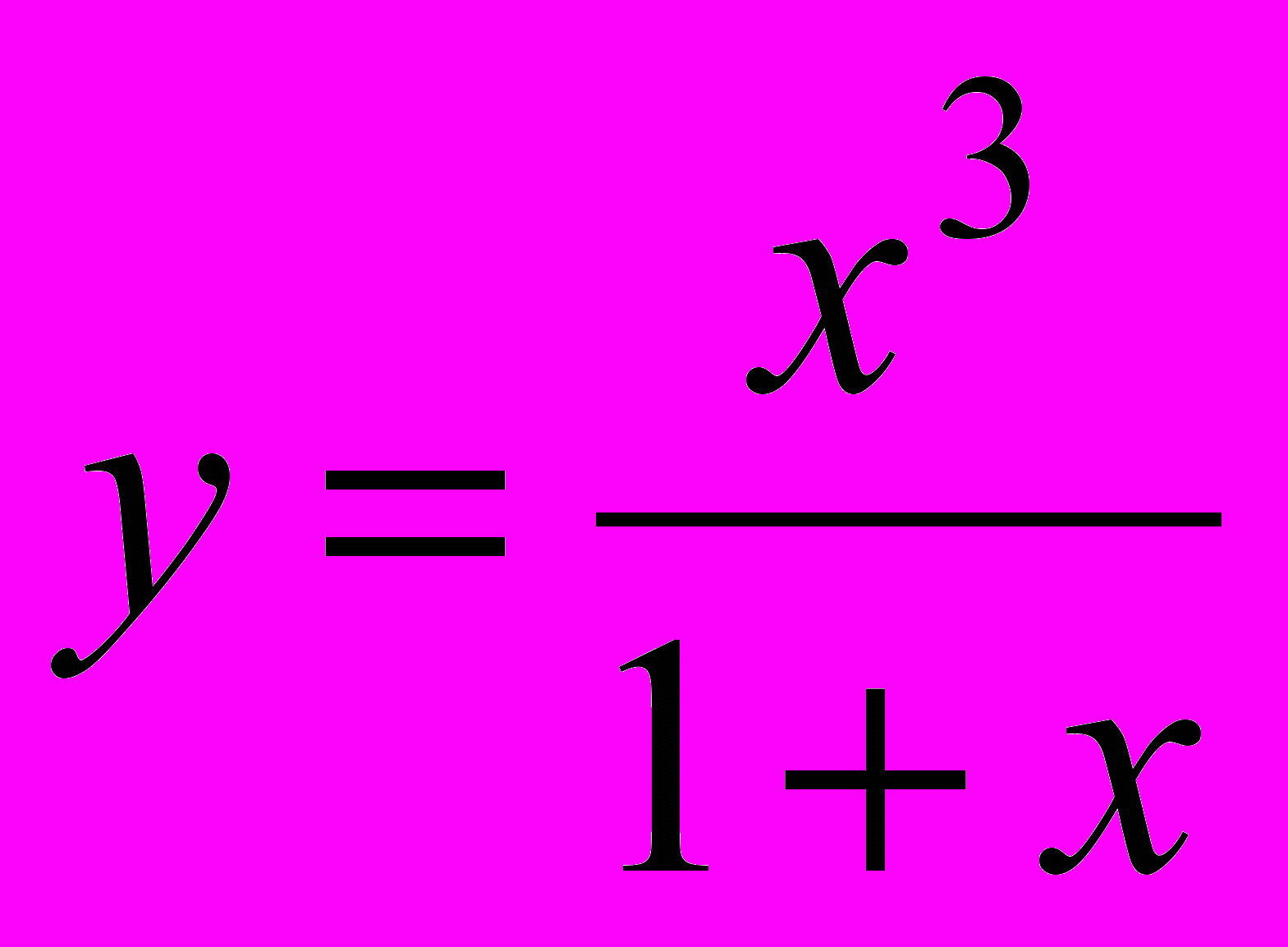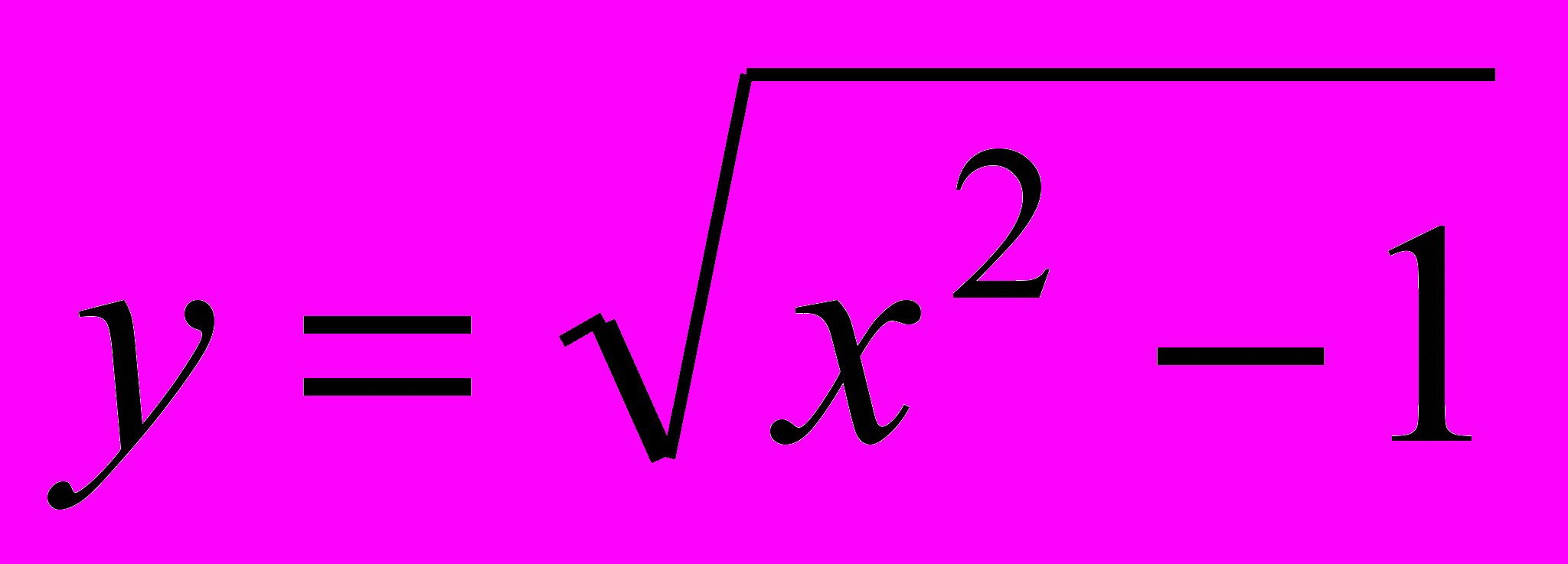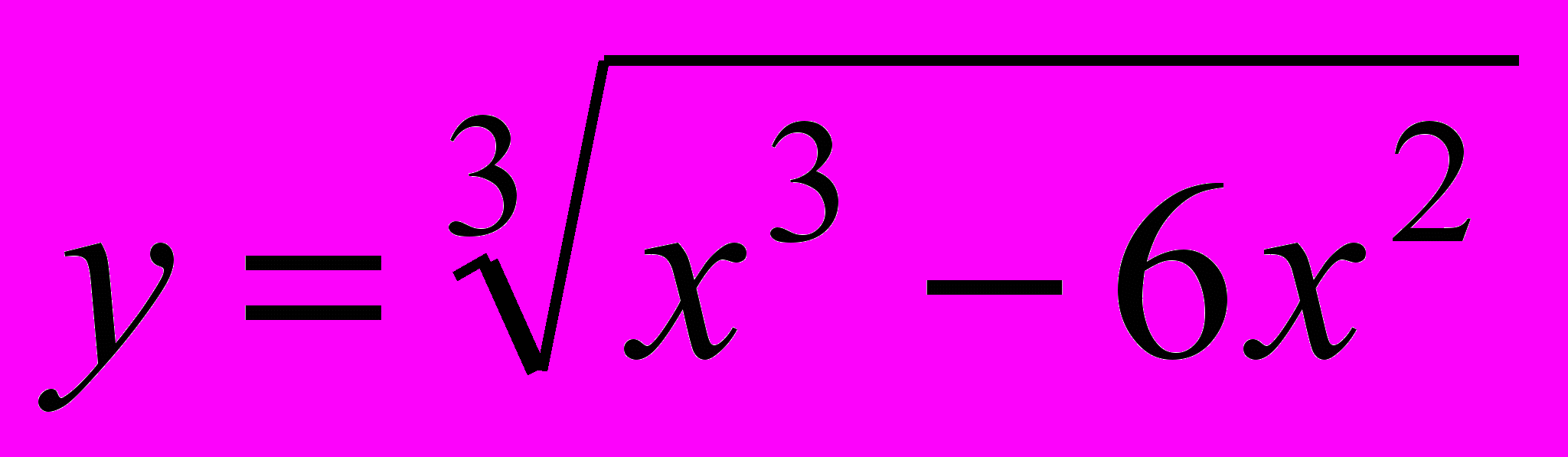).ОБРАЗЦЫ БИЛЕТОВ:
БИЛЕТ № 1
1. Приращения аргумента и функции, определение производной функции в точке, физический смысл производной.
2. Определение возрастания функции в точке, критерий нестрогого возрастания (сформулировать, доказать).
3. Дать определение наклонной асимптоты графика функции, найти наклонные асимптоты к графику функции
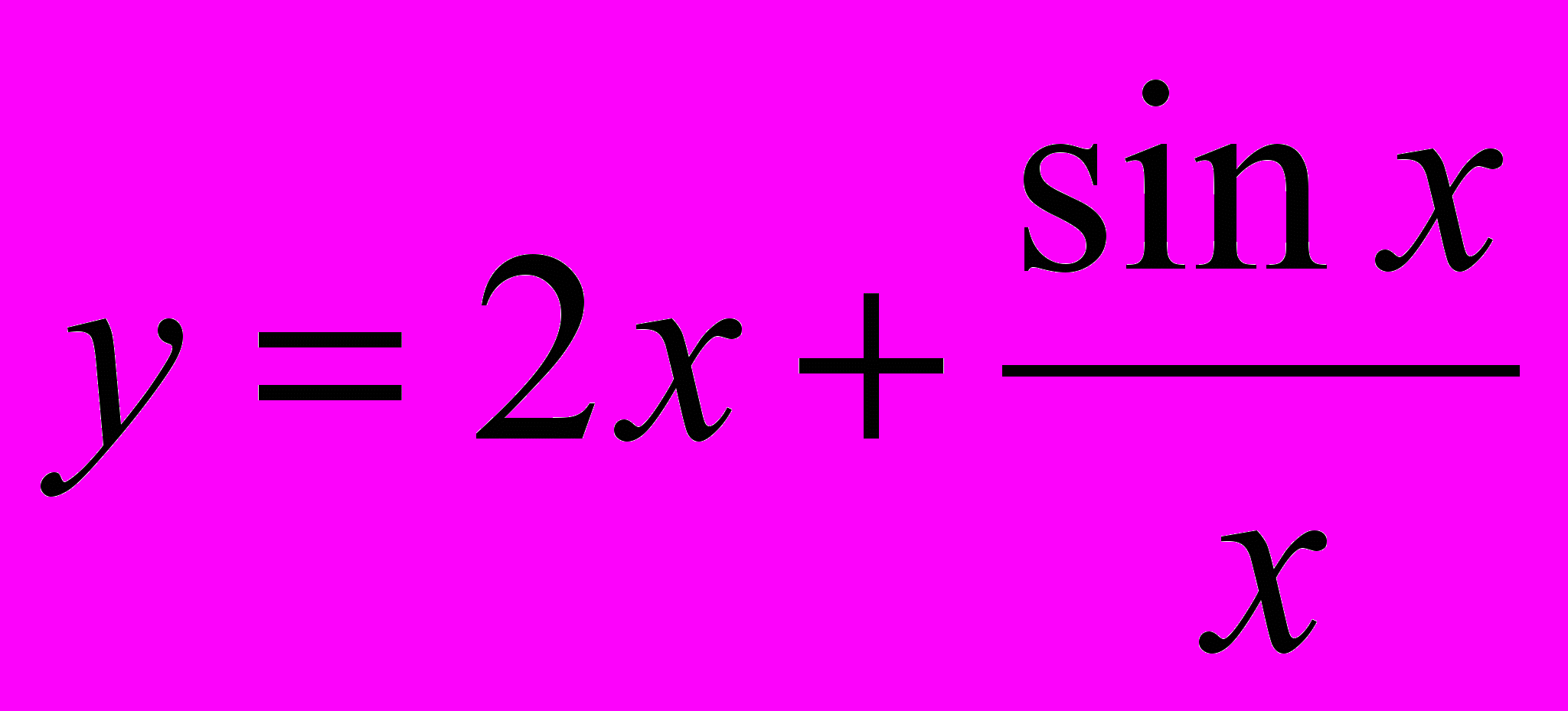.БИЛЕТ № 2
1 Определение точки перегиба графика функции, достаточное условие (формулировка).
2 Приращения аргумента и функции, определение производной функции в точке, геометрический смысл производной (доказать).
3. Издержки производства товара определяются функцией
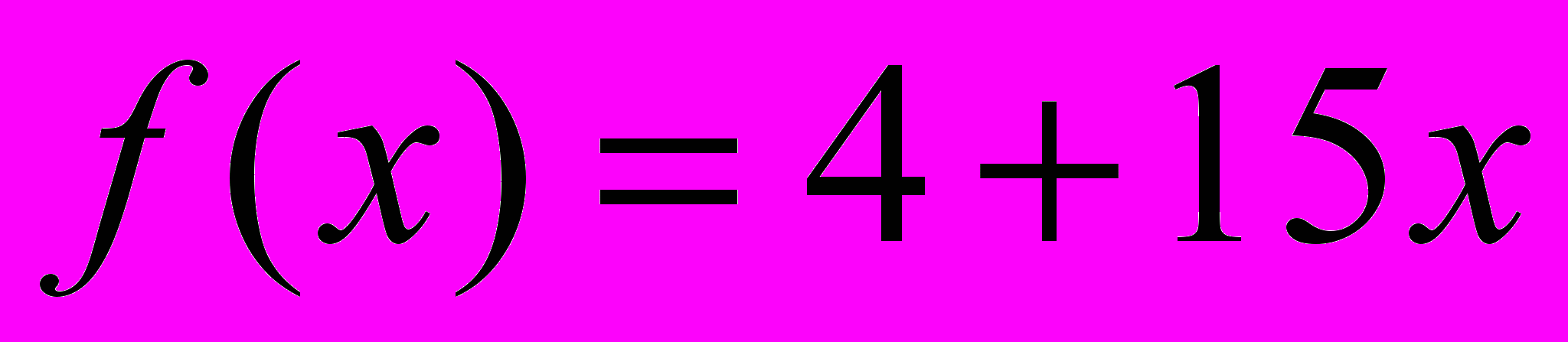, функция спроса (цена на товар) имеет вид 
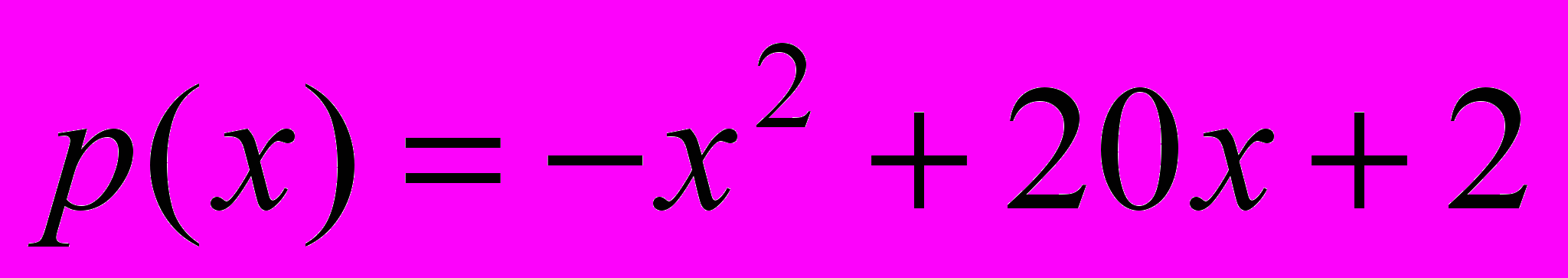, x – объем произведенного товара. Определить объем товара, при котором полученная прибыль будет максимальной.БИЛЕТ № 3
1 Определение точки перегиба графика функции, необходимое условие (формулировка).
2. Основные правила дифференцирования (теоремы о производной суммы, произведения, частного – сформулировать, теорему о производной произведения доказать).
3. Составить уравнение касательной к графику параболы
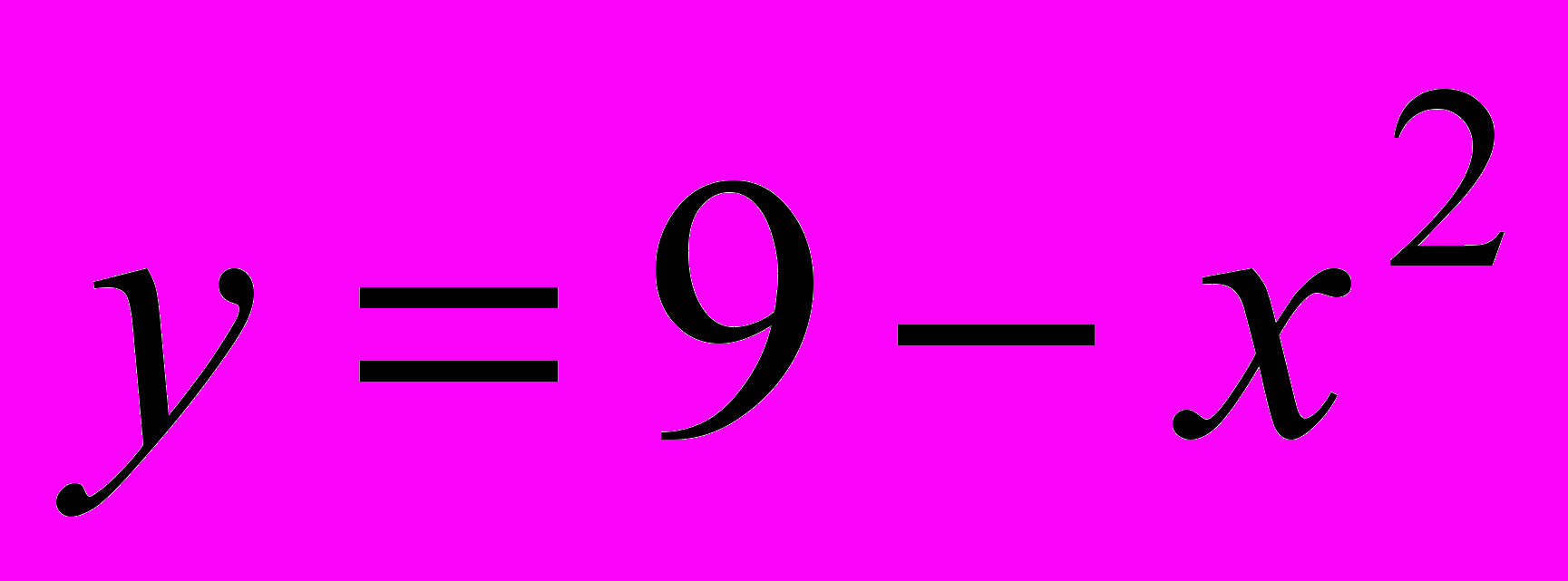в точках ее пересечения с осью OX.