«Теория вероятностей»

Вид материала

Документы

Содержание Ориентировочные (укрупненные) вопросы к зачету по «Анализу данных в социологии» (зимняя зачетная сессия на третьем курсе)

Подобный материал:

• Примерная программа наименование дисциплины «теория вероятностей и математическая статистика», 165.37kb.
• Конспект лекций по курсу "Теория вероятностей и математическая статистика", 1417.24kb.
• Рабочая учебная программа дисциплины (модуля) Теория вероятностей и математическая, 217.23kb.
• Рабочая программа дисциплины "теория вероятностей и математическая статистика", 112.61kb.
• Рабочая программа учебной дисциплины теория вероятностей и математическая статистика, 830.1kb.
• Программа курса лекций "Теория вероятностей и математическая статистика", 18.69kb.
• Рабочая программа учебной дисциплины «Теория вероятностей и математическая статистика», 165.42kb.
• Теория информации, 26.84kb.
• Теория вероятностей и математическая статистика Лектор 2010/11 уч года: д ф. м н.,, 41.34kb.
• Название курса, 73.05kb.

Ориентировочные (укрупненные) вопросы

к зачету по «Анализу данных в социологии»

(зимняя зачетная сессия на третьем курсе):

1. Таблицы сопряженности и меры связи признаков.
   
2. Сравнительный анализ различных мер связи в таблицах сопряженности.
   
3. Модель дисперсионного анализа в анализе данных социологического исследования.
   
4. Модель латинского квадрата в планировании социологического исследования.
   
5. Модель регрессионного анализа в анализе данных социологического исследования.
   
6. Модель номинального регрессионного анализа при проведении социологического исследования.
   
7. Оценивание качества регрессионной модели при проведении социологического исследования.
   
8. Использование понятий полной, множественной, частной корреляции при интерпретации данных социологического исследования.
   
9. Модель главных компонентов в анализе данных социологического исследования.
   
10. Модель факторного анализа в анализе данных социологического исследования.
    
11. Интерпретация результатов факторного анализа с помощью атрибутивной карты восприятия.
    
12. Модель канонических корреляций в анализе данных социологического исследования.
    
13. Модель кластерного анализа данных социологического исследования.
    
14. Модель дискриминантного анализа данных социологического исследования.
    
15. Модель конджойнт-анализа данных социологического исследования.
    
16. Модель пат-анализа данных социологического исследования.
    
17. Модель лонгитюдного анализа данных социологического исследования.
    
18. Модель контент-анализа данных социологического исследования.
    

Некоторые вспомогательные

вероятностно-статистические таблицы


Таблица 1. Биномиальная случайная величина Bi (n;p).


В таблице приведены значения биномиальных вероятностей (вероятностей для количества «успехов» 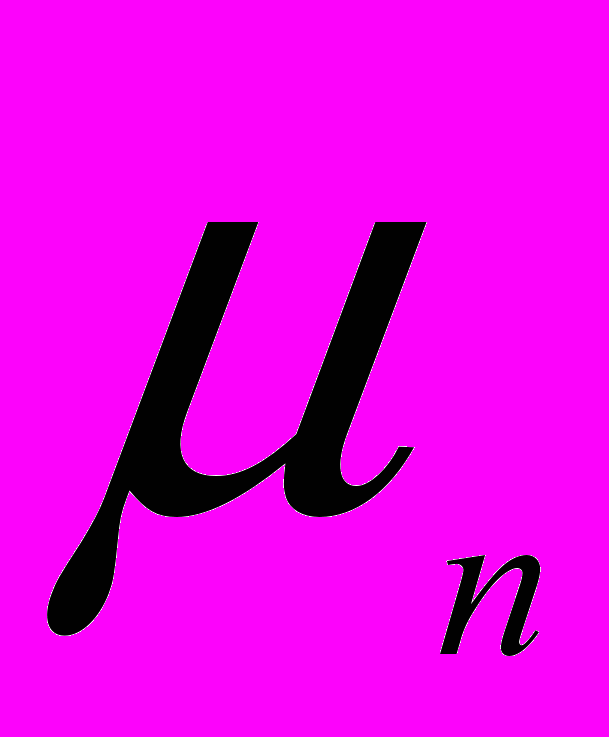в схеме Бернулли)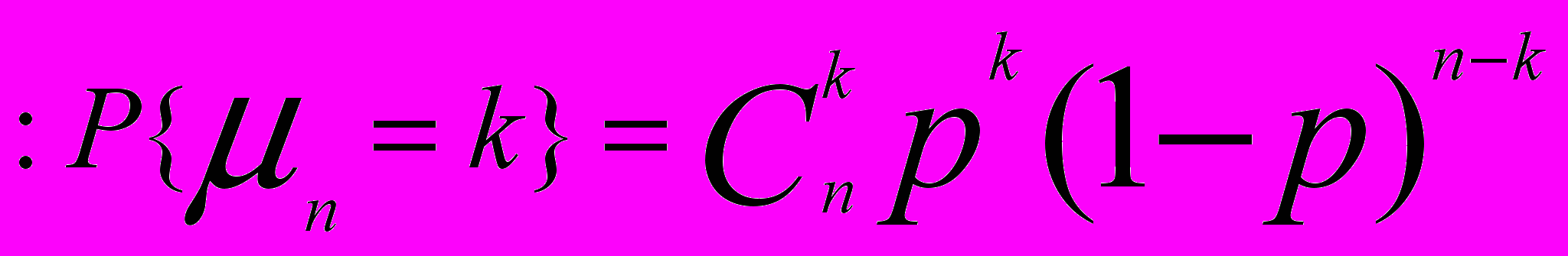, k=0, 1, 2, …, n, при некоторых значениях количества испытаний n схемы Бернулли и вероятности «успеха» p в одном испытании (значения биномиальных вероятностей приведены с округлением до тысячных долей единицы).


n=5

p k	0,1	0,2	0,3	0,4	0,5
0	0,590	0,328	0,168	0,078	0,031
1	0,328	0,410	0,360	0,259	0,156
2	0,073	0,205	0,309	0,346	0,313
3	0,008	0,051	0,132	0,230	0,313
4	0,000	0,006	0,028	0,077	0,156
5	0,000	0,000	0,002	0,010	0,031

n=10

p k	0,1	0,2	0,3	0,4	0,5
0	0,349	0,107	0,028	0,006	0,001
1	0,387	0,268	0,121	0,040	0,010
2	0,194	0,302	0,233	0,121	0,044
3	0,057	0,201	0,269	0,215	0,117
4	0,011	0,088	0,200	0,251	0,205
5	0,001	0,026	0,103	0,201	0,246
6	0,000	0,006	0,037	0,111	0,205
7	0,000	0,001	0,009	0,042	0,117
8	0,000	0,000	0,001	0,011	0,044
9	0,000	0,000	0,000	0,002	0,010
10	0,000	0,000	0,000	0,000	0,001

n=15

p k	0,1	0,2	0,3	0,4	0,5
0	0,206	0,035	0,005	0,000	0,000
1	0,343	0,132	0,031	0,005	0,000
2	0,267	0,231	0,092	0,022	0,003
3	0,129	0,250	0,170	0,063	0,014
4	0,043	0,188	0,219	0,127	0,042
5	0,010	0,103	0,206	0,186	0,092
6	0,002	0,043	0,147	0,207	0,153
7	0,000	0,014	0,081	0,177	0,196
8	0,000	0,003	0,035	0,118	0,196
9	0,000	0,001	0,012	0,061	0,153
10	0,000	0,000	0,003	0,024	0,092
11	0,000	0,000	0,001	0,007	0,042
12	0,000	0,000	0,000	0,002	0,014
13	0,000	0,000	0,000	0,000	0,003
14	0,000	0,000	0,000	0,000	0,000
15	0,000	0,000	0,000	0,000	0,000

n=20

p k	0,1	0,2	0,3	0,4	0,5
0	0,122	0,012	0,001	0,000	0,000
1	0,270	0,058	0,007	0,000	0,000
2	0,285	0,137	0,028	0,003	0,000
3	0,190	0,205	0,072	0,012	0,001
4	0,090	0,218	0,130	0,035	0,005
5	0,032	0,175	0,179	0,075	0,015
6	0,009	0,109	0,192	0,124	0,037
7	0,002	0,055	0,164	0,166	0,074
8	0,000	0,022	0,114	0,180	0,120
9	0,000	0,007	0,065	0,160	0,160
10	0,000	0,002	0,031	0,117	0,176
11	0,000	0,000	0,012	0,071	0,160
12	0,000	0,000	0,004	0,036	0,120
13	0,000	0,000	0,001	0,015	0,074
14	0,000	0,000	0,000	0,005	0,037
15	0,000	0,000	0,000	0,001	0,015
16	0,000	0,000	0,000	0,000	0,005
17	0,000	0,000	0,000	0,000	0,001
18	0,000	0,000	0,000	0,000	0,000
19	0,000	0,000	0,000	0,000	0,000
20	0,000	0,000	0,000	0,000	0,000

Таблица 2. Пуассоновская случайная величина Po (λ).

В таблице приведены значения пуассоновских вероятностей 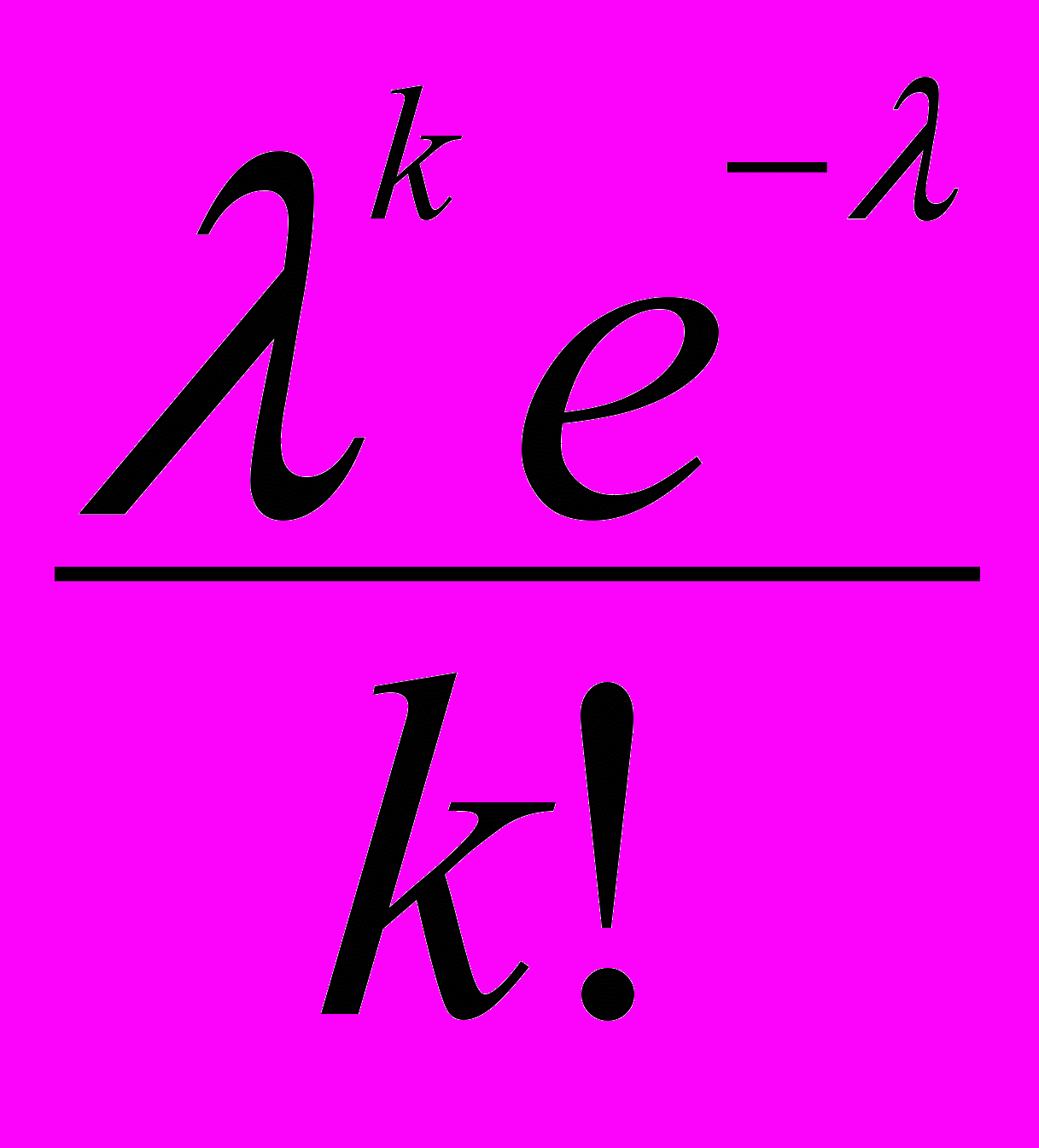при некоторых значениях параметра k (количество «успехов» в «длинной»: n→∞ схеме Бернулли с «редкими»: p→0 успехами) и параметра λ (λ=np), а также значения суммы вида 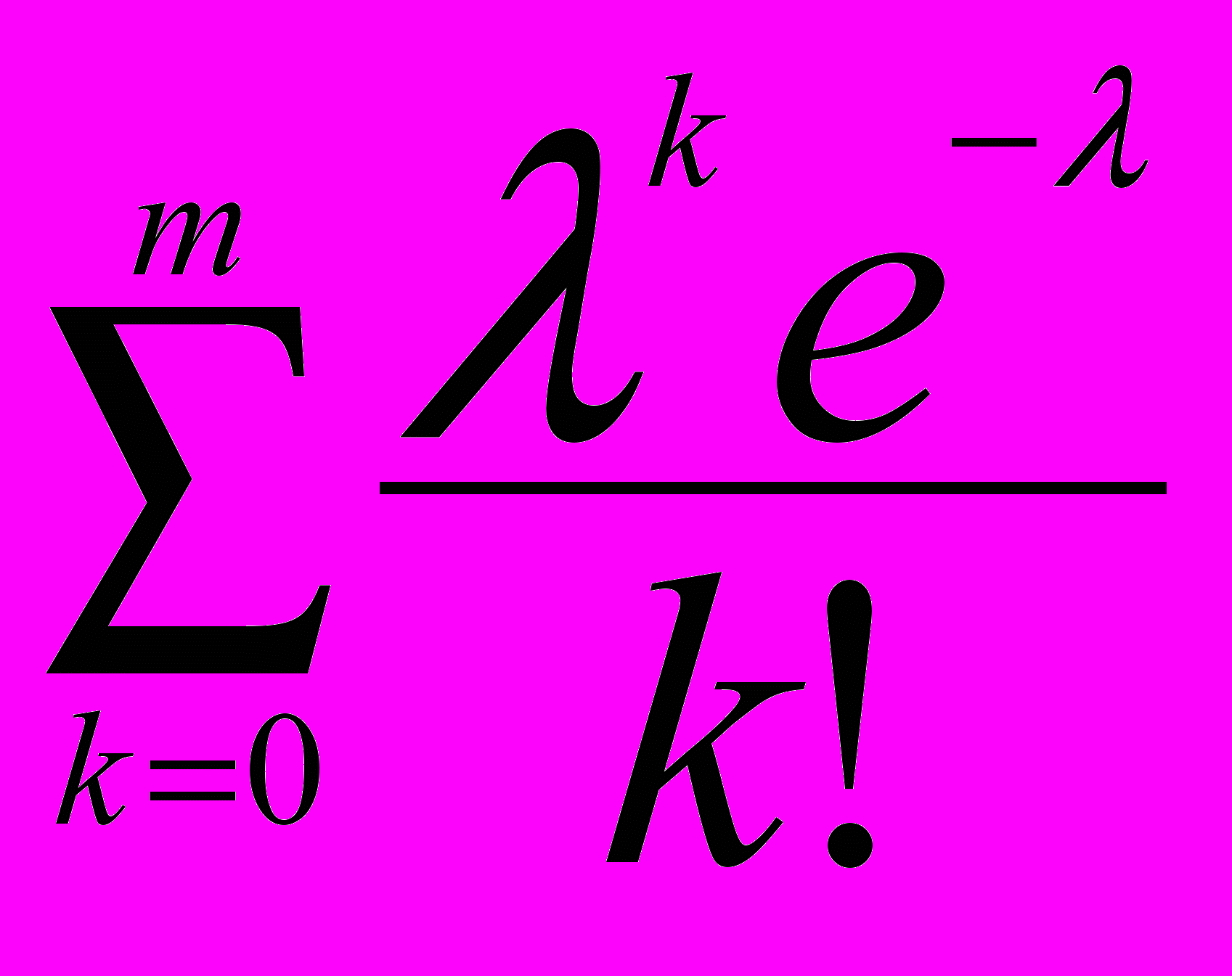при некоторых значениях параметров λ и m (значения пуассоновских вероятностей и их сумм приведены с округлением до сотых долей единицы).


Значения величины

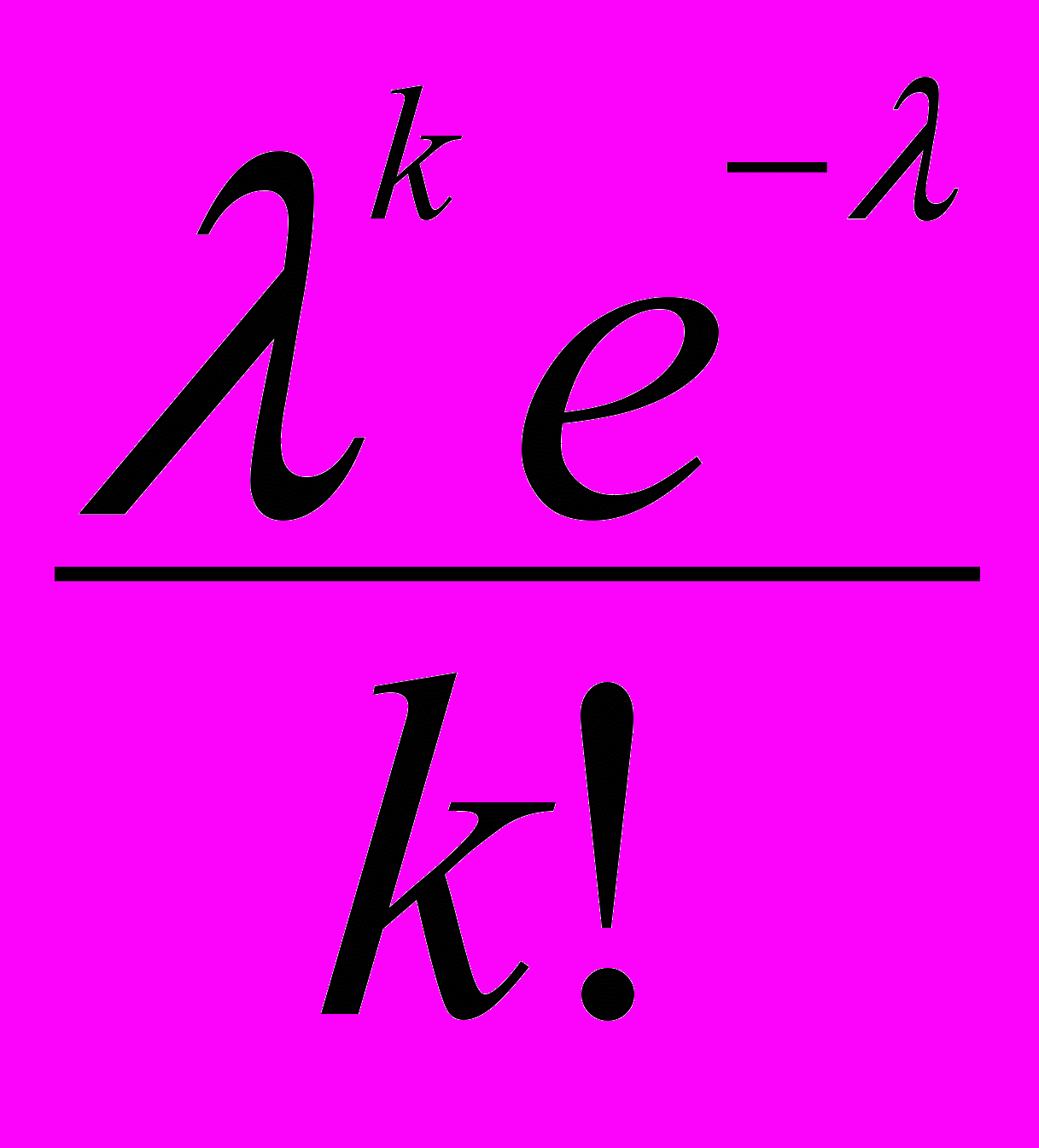
λ k	0,5	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0
0	0,61	0,37	0,14	0,05	0,02	0,01	0,00	0,00	0,00	0,00
1	0,30	0,37	0,27	0,15	0,07	0,03	0,01	0,01	0,00	0,00
2	0,08	0,18	0,27	0,22	0,15	0,08	0,04	0,02	0,01	0,00
3	0,01	0,06	0,18	0,22	0,20	0,14	0,09	0,05	0,03	0,01
4	0,00	0,02	0,09	0,17	0,20	0,18	0,13	0,09	0,06	0,03
5	0,00	0,00	0,04	0,10	0,16	0,18	0,16	0,13	0,09	0,06
6	0,00	0,00	0,01	0,05	0,10	0,15	0,16	0,15	0,12	0,09
7	0,00	0,00	0,00	0,02	0,06	0,10	0,14	0,15	0,14	0,12
8	0,00	0,00	0,00	0,01	0,03	0,07	0,10	0,13	0,14	0,13
9	0,00	0,00	0,00	0,00	0,01	0,04	0,07	0,10	0,12	0,13
10	0,00	0,00	0,00	0,00	0,01	0,02	0,04	0,07	0,10	0,12
11	0,00	0,00	0,00	0,00	0,00	0,01	0,02	0,05	0,07	0,10
12	0,00	0,00	0,00	0,00	0,00	0,00	0,01	0,03	0,05	0,07
13	0,00	0,00	0,00	0,00	0,00	0,00	0,01	0,01	0,03	0,05
14	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,01	0,02	0,03
15	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,01	0,02
16	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,01
17	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,01
18	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00

Значения величины