Рецензенты: И. Б. Левицкая проректор по научной работе гоу «Государственный институт развития образования», к п. н., доцент
| Вид материала | Книга |
- Н. А. Добролюбова, проректор по научной работе, 50.95kb.
- Учебно-методическое пособие удк 796/799 (075. 8) Печатается по решению ббк 74. 267., 3134.91kb.
- «Использование потенциала семьи в системе коррекционного воздействия на ребёнка», 138.16kb.
- Русские в Турции. 1920-1921, 352.95kb.
- Содержание подготовки методистов-организаторов в системе повышения квалификации работников, 284.53kb.
- Ильина Нина Федоровна,, 93.42kb.
- А. А. Левицкая, кандидат педагогических наук, доцент, 158.25kb.
- Тезисы выступления, 2699.95kb.
- Программа Челябинск 2011 г. Министерство образования науки Российской Федерации Южно-Уральский, 580.08kb.
- С. Х. Мухаметгалиева Елабуга, Елабужский государственный педагогический университет, 3598.14kb.
471. Определите площадь передней стены сарая, изображенного на рис. 8.
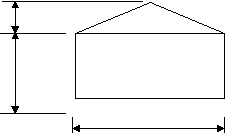2 м4 м
8 м
Рис. 8
8 · 4 + 8 · 2 : 2 = 40 (м2.)
472. На участке, который имеет форму прямоугольного треугольника АВС (рис.9), отгородили часть АЕF. Во сколько раз площадь всего участка больше площади отгороженной части?
С
20 м F
4 м
В Е А
60 м
12 м
^ Рис. 9
Ответ :(60 · 20 : 2): (12 · 4 : 2) = 600 : 24 = 25 (раз.)
- Прямоугольник разделен на квадраты. На некоторых квадратах отмечены шесть точек. Необходимо разрезать прямоугольник вдоль сторон квадратов на 6 одинаковых частей так, чтобы в каждой части было по одной точке.
Ответ:
- Р
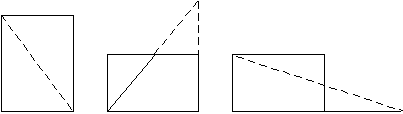азрезать прямоугольник прямой линией на две части так, чтобы из них можно было сложить треугольник.
Ответ:
- Деревянный окрашенный куб с ребром 3 см распилили на кубические сантиметры. Сколько среди них кубиков, которые окрашены с трех сторон?
8 кубиков.
- К
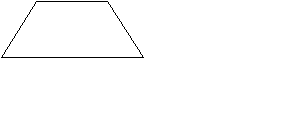ак разрезать фигуру (см.рисунок 10) на две части так, чтобы из них можно было сложить прямоугольник.
Ответ:
Рис. 10
- Прямоугольный брусок, окрашенный в зеленый цвет, имеет измерения 12 см, 8 см и 6 см. Этот брусок распилили на кубики, каждое ребро которых 2 см. Сколько получилось кубиков у которых окрашены в зеленый цвет: а) три грани; б) две грани; в) одна грань; г) ни одна грань не окрашена в зеленый цвет?
6 · 3 · 4 = 72 (куб) – всего; а) 8; б) 2 · 4 + 4 · 4 + 4 · 1 = 28; в) 4 · 2 + 2 · 2 + 8 · 2 = 28; 72 – (8 + 28 + 28) = 8.
478. Как разрезать фигуру, показанную на (рис.11), на две одинаковые части?
Ответ:
Рис. 11
479. Арбуз разрезали на четыре части и съели. Получилось пять корок. Может ли такое быть?
Если постараться, то можно из арбуза вырезать кусок в виде столбика, идущего сквозь весь арбуз. У этого куска будут две корки, соединяемые арбузной мякотью. Оставшуюся часть арбуза можно разрезать на «нормальные» куски.
480. Четыре страны имеют форму треугольников. Как расположены страны одна относительно другой, если у каждой из них есть общие границы с тремя другими. Нарисуйте.
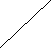Ответ:4 2
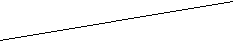
1
3
481. Сколько одинаковых квадратов надо взять, чтобы из них можно было сложить в два раза больший квадрат? Сколько одинаковых кубиков надо для составления в два раза большего куба?
Если считать, что в два раза больший квадрат – это квадрат, сторона которого в два раза больше стороны исходного квадрата, то для его получения надо взять четыре одинаковых исходных квадрата. А для получения куба надо взять 8 кубиков.
482. На какое самое большое число частей можно разрезать блин тремя разрезами? Сколько частей может получиться при трех разрезах каравая?
Блин можно разделить на семь частей (рис. 12). а); в отличие от блина каравай не плоский и его сначала можно разрезать горизонтально, а потом вертикально (рис. 12, б). Таким образом, каравай можно разрезать на восемь частей.
а) б)
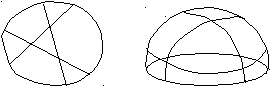
Рис. 12
- Можно ли куб завернуть в букву Т в один слой? Если да, то нарисуйте эту букву. Укажите её размеры, если ребро куба равно 1 см.
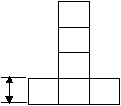
Буква Т составлена из шести квадратов со стороной 1 см.
1 СМ484. Из фигур изображенных на рисунке 13, выберите те, которые являются развертками куба, и перенесите их в тетрадь. Объясните, почему вы выбрали именно их.
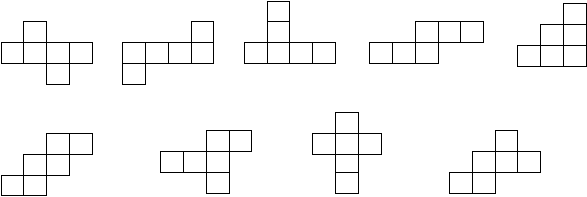
1 2 3 4 5
6 7 8 9
Рис. 13
^ Развертками куба являются 1, 2, 4, 6 – 9.
- Дана развертка куба (рис. 14). Какие из изображенных кубиков на рисунке 15, а – в можно из развертки склеить кубики? Выберите кубик и обоснуйте выбор.
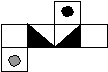
Рис. 14
а) б) в)Рис. 15
Ответ: Из представленной развертки можно склеить кубики а) и б)
486. Имеется куб со стороной 3 см. Сколько надо сделать распилов, чтобы распилить его на кубики со стороной в 1 см?
^ Шесть распилов.
- На рисунке 16, показан способ разрезания квадрата со стороной в четыре клетки по сторонам клеток на две равные части. Найдите пять других способов. Сколько существует способов разрезания квадрата на две равные части линиями, идущими по сторонам маленьких квадратиков?
Рис. 16
Ответ:
- Эта задача посложнее, так как фигура на рисунке 17, которую также нужно разрезать на две равные части, не такая простая.
Ответ:
Рис. 17
489. Представленные ниже фигуры (рис. 18) разрежьте на две равные части.
З а м е ч а н и е. Разрезать можно не только по сторонам, но и по диагоналям клеточек.
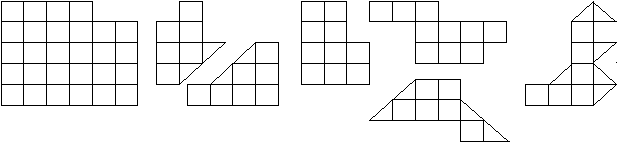
Рис. 18
Ответ:
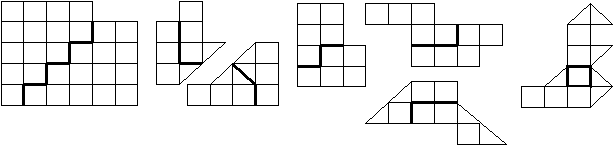
490. Прямоугольный лист бумаги разделили двумя разрезами на два листа треугольной формы и два четырехугольной. Как это сделали?
Ответ:
491. Дан треугольник, длины сторон которого равны 7, 12, 9 см. Объясните, как построить отрезок, соединяющий его вершину и противоположную сторону, длиной в 9 см так, чтобы периметр двух полученных треугольников был одинаков?
I способ
Так как в полученных треугольниках сторона AD общая, то для того, чтобы периметры треугольников были равны, необходимо, чтобы сторона в 9 см была разбита на части, разность длин которых равнялась бы разности двух сторон (12 – 7 = 5 см). Исходя из этого, число 9 следует представить в виде суммы двух слагаемых, одно из которых на 5 больше другого. Числами, удовлетворяющими этому условию, являются 2 и 7. Таким образом, получаем следующее решение:
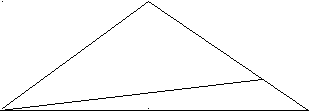В7 см 7 см
D
2 см
А 12 см С
II способ
Решение этой задачи будет легко найдено, если периметр представить в виде суммы отрезков:
PABD = AB + BD + DA;
A B D A A C D A
PADC = AC + CD + DA.
- 12 – 7 = 5 (см) – на столько длина отрезка BD должна быть больше отрезка CD.
- 9 – 5 = 4 (см) – длина двух отрезков CD.
- 4 : 2 = 2 (см) – длина отрезка CD.
- 2 + 5 = 7 (см) – длина отрезка BD.
492. В прямоугольнике ABCD периметр треугольников, из которых он состоит, равен 180 см. BK = KC = AE = ED. AK = KD = 17. Найдите периметр прямоугольника, у которого одна сторона в 2 раза больше длины отрезка AB, а другая сторона равна длине отрезка BC.
К
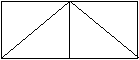В СА D
Е
I способ
Данную фигуру можно дополнить до прямоугольника, периметр которого необходимо найти.
^ Периметр фигуры NBCM равен 2 · АВ + 2 · ВК + 2 · CD + 2 · DE = 2 · (AB + BK) + 2 · (CD + DE). Периметр этой фигуры от исходного периметра отличается на длину
К
В CА Е D
N М
О
четырех отрезков АК (17 · 4 = 68). Таким образом, периметр искомой фигуры равен 180 – 68 = 112 см.
II способ
Исходя из условия задачи, можно определить периметр одного треугольника. Он равен АВ + ВК + 17. Тогда можно составить уравнение (АВ + ВК + 17) · 4 = 180. Отсюда находим, что АВ + ВК = 28. Умножая обе части последнего равенства на 2, получим: 2 · АВ + 2 · ВК = 56 или 2 · (АВ + ВС) = 56. Тогда периметр прямоугольника равен 2 · 56 = 112 см.
493. За всю историю шахмат было 19 чемпионов мира мужчин и женщин. Чемпионов мужчин было на 7 больше, чем женщин. Сколько мужчин и сколько женщин были чемпионами мира по шахматам?
Используем схематический чертеж для краткой записи условия задачи. Обозначим число мужчин и женщин чемпионов определенными отрезками. Первый отрезок должен быть больше, чем второй.
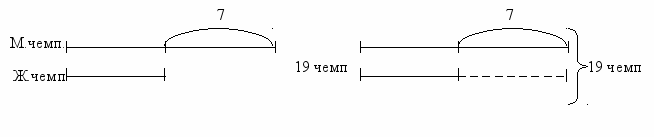а) б)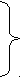
^ Из данной краткой записи можно определить решение:
1 способ.
- 19 – 7 = 12 – удвоенное количество женщин чемпионок;
2) 12 : 2 = 6 (чемп.) – женщин;
^ 3) 6 + 7 = 13 (чемп.) – мужчин;
В данном решении можно объединить первое и второе действие для удобства объяснения.
1) (19 – 7) : 2 = 6 (чемп.) – женщин;
2) 6 + 7 = 13 (чемп.) – мужчин или
19 – 6 = 13 (чемп.) – мужчин.
2 способ
1) 19 + 7 = 26 (чемп.) – удвоенное количество мужчин чемпионов;
2) 26 : 2 = 13 (чемп.) – мужчин;
^ 3) 13 – 7 = 6 (чемп.) – женщин или
19 – 13 = 6 (чемп.) – женщин.
Другая запись:
1) (19 + 7) : 2 = 13 (чемп.) – мужчин;
2) 13 – 7 = 6 (чемп.) – женщин или
19 – 13 = 6 (чемп.) – женщин.
494. Витя и Сережа проплыли вместе 19 метров. Витя проплыл на 5 метров больше, чем Сережа. Сколько метров проплыл каждый мальчик?
12м; 7м.
495. Композитор Чайковский П.И. написал на 1 балет больше, чем Хачатурян. Сколько балетов написал каждый из этих композиторов, если оба вместе написали 5 балетов?
^ 3 балета написал П.И.Чайковский и 2 балета Хачатурян .
496. У бабушки два внука: Коля и маленький Олег. Бабушка купила им 16 конфет и сказала Коле, чтобы он дал Олегу на 2 конфеты больше, чем себе. Как Коля должен разделить конфеты?
7 конфет; 9 конфет.
497. Прямой отрезок длиной 30 см разрезали на две части так, что одна часть в 4 раза больше другой. Найти длину каждой части.
6 см; 24 см.
498. У песца 30 входов в нору. Количество входов, которые он использует в два раза меньше чем те, которые он не использует. Сколько входов в нору не использует песец?
^ Задача легко решается схематическим изображением условия в виде:
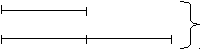Исп. норы30 входов
Неисп. норы в нору
Решение:
30 : 3 = 10 (нор) – использует песец;
10 · 2 = 20 (нор) – не использует песец.
499. У планеты Земля и планеты Нептун вместе 10 спутников. У планеты Нептун в 9 раз больше спутников, чем у планеты Земля. Сколько спутников у планеты Нептун?
9 спутников.
500. В Олимпийских играх 1912 года участвовало 24 русских легкоатлета и гимнаста. Гимнастов было в 7 раз больше, чем легкоатлетов. Сколько было гимнастов?
21.
501. У Тани и Саши было одинаковое количество книг. Сначала Саша подарил Тане одну книгу, а затем Таня подарила Саше три книги. На сколько книг больше стало у Саши, чем у Тани?
У Саши стало на 4 книги больше.
502. Длина прямоугольника на 2 см больше, чем его ширина. Нарисуйте этот прямоугольник, если его полупериметр равен 10см.
Длина – 6 см, ширина – 4 см.
503. Италию омывают на 3 моря больше, чем Германию. Всего эти две страны омываются 7 морями. Сколько морей омывают каждую страну?
^ 5 морей; 2 моря.
504. Папа-пингвин нянчит своего малыша в два раза меньше дней, чем он высиживает яйцо. Всего 90 дней папа-пингвин заботится о малыше и высиживает яйцо. Сколько дней он высиживает яйцо?
60 дней.
505. Мартышке в зоопарке добавляет в пищу определенное количество масла в сутки, макаке добавляют столько же, сколько мартышке, а горилле столько, сколько макаке и мартышке вместе. Сколько растительного масла добавляют в пищу ежедневно горилле, если всем троим вместе добавляют 20 г масла?
10 г.
506. Одно число в 4 раза больше, чем другое, и на 30 больше, чем то же число. Найти эти два числа.
10; 40.
507. Дед, отец и сын во время прогулки встретили знакомого, который спросил их, сколько им лет. «Нам 121 год», – ответил за всех дед и важно зашагал вперед. Тогда знакомый, продолжая интересоваться их возрастом, спросил отца: «Ну, скажите же, сколько вам лет?» – «Мне вместе с сыном 44 года», – отвечал отец, – «а сын на 28 лет моложе меня». Так знакомому и не пришлось узнать, сколько лет каждому из них. Не сообразишь ли ты?
77 лет; 36 лет; 8 лет.
508. В портфеле 15 тетрадей: в одну линейку, в две линейки и в клетку. Тетрадей в клетку на 10 больше, чем тетрадей в одну линейку. Сколько может быть в портфеле тетрадей в одну линейку, в две линейки, в клетку?
^ 12 тетрадей в клетку, 2 тетради в одну линейку, 1 тетрадь в две линейки или 11 тетрадей в клетку, 1 тетрадь в одну линейку и 3 тетради в две линейки.
509. Увеличивая на 4 утроенное какое-то натуральное число, получим число на 28 больше, чем первоначальное число. Найди соответствующее число.
12.
510. Если количество башен Кремля, увенчанных рубиновыми звездами умножить на 4, то получится тот же результат, что и при прибавлении к нему числа 15 (15 - количество остальных башен Кремля). Сколько всего башен имеет Кремль?
20.
511. Среднее арифметическое между числом, его половиной и его четвертью составляет число 21. Найди это число.
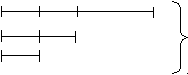
21 · 3
Ответ: 36.
512. Школьник прочитал 18 страниц за три дня. Если бы в первый день он прочитал на одну страницу больше, а во второй день на одну страницу меньше, то каждый день он читал бы поровну. По сколько страниц читал каждый день школьник?
1 д. – 5 стр.; 2 д. – 6 стр.; 3 д. – 7 стр.
513. Щука вчетверо тяжелее окуня, но на 2 кг легче судака. Если к весу всех троих прибавить вес корзины, в которой они лежат – 1 кг 250 г, то получится 10 кг. Определить вес каждой рыбы в отдельности?
10000 – 1250 = 7500(г)
Щ
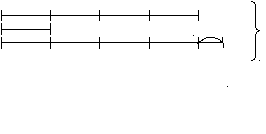.О. 2 7500 г
С.
Щука – 3 кг; Сом – 5 кг; Окунь – 750 г;
514. Мы с Володей собирали марки. У нас вместе на 25 марок больше, чем у меня, и на 15 марок больше, чем у Володи. Сколько марок у каждого из нас и сколько марок у нас вместе?
^ 15 и 25; вместе 40 марок.
515. На вопрос учеников о дне своего рождения учитель математики ответил так: «Если сложить день и номер месяца моего рождения, то получится 20; если из дня рождения вычесть номер месяца рождения, то получится 14; если к произведению дня и номера месяца моего рождения прибавить 1900, то получится год моего рождения». Когда родился учитель математики?
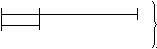
20
14
Ответ: 17 марта 1951.
516. Через пять лет, Женя будет вдвое старше, чем сейчас. Сколько лет ему сейчас?
5 лет.
517. Красная Шапочка несла бабушке 14 пирожков с мясом, с грибами и с капустой. Пирожков с капустой на два больше, чем пирожков с мясом. А пирожков с грибами в два раза больше, чем пирожков с мясом. Сколько пирожков с грибами, с мясом и с капустой в отдельности?
^ С грибами – 6 пир.; с мясом – 3 пир.; с капустой – 5 пир.
518. Попрыгунья Стрекоза половину времени каждых суток красного лета спала, третью часть времени каждых суток танцевала, шестую часть – пела. Остальное время она решила посвятить подготовке к зиме. Сколько часов в сутки Стрекоза готовилась к зиме?
0 часов.
519. У двух детей были орехи. У одного было на 30 орехов меньше, чем у другого. На сколько орехов будет меньше у первого, чем у второго, если он второму отдаст 16 орехов?
30 + 16 + 16 = 62 (ореха).
520. У первого мальчика было вдвое больше цветных карандашей, чем у второго. Когда первый мальчик купил еще 4 цветных карандаша, то у него стало цветных карандашей в 3 раза больше, чем у второго мальчика. Сколько цветных карандашей было у каждого мальчика?
8; 4.
521. На трех березках сидели 36 грачей. Когда с одной березы поднялись в воздух 4 грача, с другой 6 и с третьей 8, то на трех березках осталось грачей поровну. Сколько грачей сидело на каждой березе?
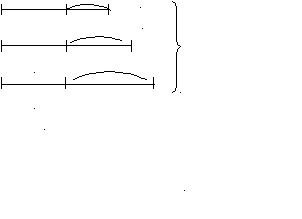4 6
36
8
I б. – 10 гр.; II б. – 12 гр.; III б. – 14 г.
522. Один рыбак поймал на 20 окуней больше, чем другой. Но когда он отдал товарищу в обмен за щуку 15 окуней, то у него их стало вдвое меньше, чем у товарища. Сколько окуней было у каждого?
15
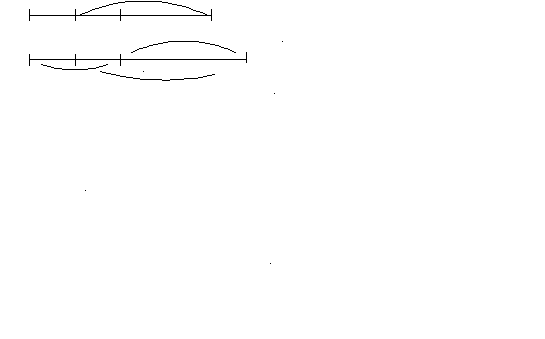
15
20
^ 1 рыбак – 5 окуней; 2 рыбак – 25 окуней.
5
23. В Японии осьминогов ловят так: на дно опускают на веревках горшки и туда забираются любопытные осьминоги. В двух горшках у одного рыбака находятся осьминоги. Если переложить из первого горшка во второй 2 осьминога, то их количество в обоих горшках станет одинаковым. А если из второго горшка переложить 2 осьминога в первый, то в первом горшке количество осьминогов станет в 3 раза больше, чем во втором. Сколько было первоначально осьминогов в каждом горшке?2
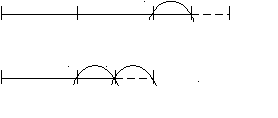
2
2 2
^ Ответ: 10 осьминогов; 6 осьминогов.
524. В XVIII веке в России был построен Оперный театр. Для постройки этого театра были задействованы каменщики, живописцы, кузнецы и столяры – всего 68 человек. Какое количество мастеров каждого вида было задействовано на строительстве Оперного театра, если известно, что живописцев было на 8 больше, чем каменщиков, кузнецов на 6 меньше, чем каменщиков, а столяров на 2 человека меньше, чем каменщиков и живописцев вместе?
^ 20 живописцев; 12 каменщиков; 6 кузнецов; 30 столяров.
525. В футбольной команде 10 игроков и вратарь. Защитников на 1 больше, чем полузащитников, а нападающих столько, сколько вместе защитников и полузащитников. Сколько нападающих в футбольной команде?
5 нападающих.
526. Гонки парусных кораблей (яхт) называются регатой. Число яхт достигших финиша в регате в 5 раз больше, чем число яхт оставивших гонку из-за поломок. Число возвратившихся яхт из-за шторма в 4 раза больше, чем число яхт прекративших гонку из-за поломок. Сколько яхт возвратились из-за шторма, если общее количество яхт участвовавших в регате равно 30?
12 яхт.
527. Царь Борис Годунов во время приема послов надевал на себя одежду, шапку и башмаки украшенные драгоценными камнями. Их вес выражается тремя нечетными последовательными числами. Сколько весит одежда, шапка и башмаки в отдельности, если на царе было 9 кг груза?
^ Одежда – 5 кг; шапка – 3 кг; башмаки – 1 кг.
528. В морской битве у города Симон участвовало 22 русских и турецких корабля. Русских кораблей под командованием адмирала Нахимова было на 10 меньше, чем турецких. Сколько осталось турецких кораблей после битвы, если 15 турецких кораблей было потоплено?
1 корабль.
529. В муравейнике кроме муравьев живут некоторые виды кузнечиков и мух. Видов мух на 10 больше, чем видов кузнечиков. Среднее арифметическое числа видов мух и числа видов кузнечиков 13. Сколько видов мух гостят в муравейнике?
^ 18 видов мух.
530. После появления всходов морковка растет на 10 дней дольше, чем редис, а свекла растет 70 дней, т.е. столько сколько редис и морковка вместе. Через сколько дней можно собрать урожай редиса?
^ Через 30 дней.
531. П.И.Чайковский написал свыше 100 фортепианных пьес, в том числе циклы «Времена года» и «Детский альбом». Количество пьес включенных о «Времена года» в два раза меньше, чем количество пьес в «Детском альбоме», а количество остальных пьес на 28 больше, чем количество пьес включенных в эти два цикла. Сколько пьес содержит каждый цикл?
24; 12.
5
32. Первая в мире вооруженная ракетами подводная лодка появилась в России в 1934 году. На ней было определенное количество ракет. Если увеличить на 12 удвоенное это число, то получим число на 18 больше, чем первоначальное число. Сколько ракет было на первой вооруженной подводной лодке?12
18
^ Ответ: 6 ракет было на подводной лодке.
533. Самые крупные в мире жуки: дровосек-титан и геркулес. Их длина вместе 33 см. Самая крупная в мире бабочка-агриппина. Она вместе с дровосеком имеет длину 42 см, а вместе с геркулесом – 45 см. Найти длину этих жуков в отдельности, а также бабочки.
^ 15 см – дровосек – титан; 18 см – геркулес; 27 см – бабочка – агриппина.
534. Кот Леопольд и 2 мыши, серая и белая «отпраздновали» свою юбилейную стычку. После этого у кота и серой мышки было 15 шишек, а у 2-х мышей вместе 12 шишек, а у кота Леопольда и белой мышки – 17 шишек. Сколько шишек у каждого из них?
^ Кот Леопольд – 10 шишек; серая мышка – 5 шишек; белая мышка – 7 шишек.535. Если количество зубов улитки поделить на 5, получим тот же результат, как при вычитании 20 тысяч из этого числа. Найти количество зубов улитки.
20 тыс.
Ответ: 25 тыс. количество зубов улитки.
536. Среднее арифметическое количества месяцев, что кормят своего малыша дельфины и синие киты равно 10. Первое число на 4 меньше, чем второе. Сколько месяцев кормят своего малыша синие киты? А дельфины?
12 месяцев; 8 месяцев.
537. Разность двух чисел равна 59. Если поделить большее число на меньшее получим неполное частное 5 и остаток 7. Найди эти два числа.
Для выполнения схематической модели данной задачи, необходимо вспомнить запись деления с остатком:
a : в = d (остаток r) или a = в · d + r, где r < b;
Так как в задаче а и в неизвестные, a : в = 5 и r = 7, то, обозначив через какой-то отрезок второе число (в), зная, что, а = 5 · в + 7 получим следующую схематическую модель условия задачи:
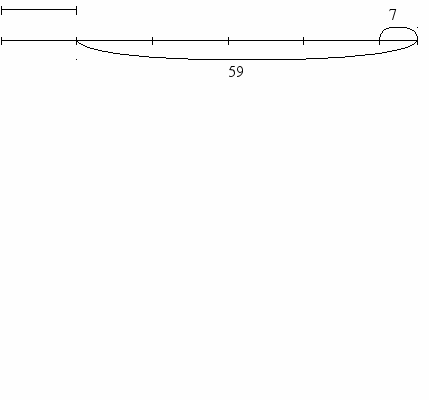а) в)
Решение:
(59 – 7) : 4 = 13
13 · 5 + 7 = 72
Проверка
72 : 13 = 5 (ост.7)
Ответ: 72; 13;
538. Сумма двух натуральных чисел равна 72, а частное при их делении равно 3. Найти эти два числа.
18; 54.
539. Если сложить количество перьев, из которых состоят хвосты двух пингвинов, а потом полученный результат поделить на 3, получим число 10. Зная, что у одно из пингвинов в хвосте на 4 пера больше, чем у другого, найдите количество перьев в хвосте каждого пингвина.
^ 13 перьев в хвосте у одного пингвина; 17 перьев у другого.
540. Петя поймал в Днестре 3 карася массой 1260г. Найти массу каждого карася, если она выражена тремя последовательными натуральными числами.
419 г; 420г; 421 г.
541. Вычитая из утроенного первого числа второе число, получим 140. Зная, что разность этих двух чисел равна 30, найти эти два числа.
55; 25.
542. Сумма двух натуральных чисел равна 100. Неполное частное при делении этих чисел это число 2 и остаток 10. Найти эти два числа.
10100
70; 30.
543. Около медузы плавали 45 рыб: ставрида и треска. Если сложить утроенное первое число ставрид и удвоенное число рыбок трески, то получим 100 рыбок. Найти количество ставрид и количество рыбок трески, плавающих около медузы.
45 
45 100
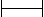
Ответ: 10 ставрид и 35 рыбок трески.
544. Во время битвы на Куликовом поле сошлись 16 русских и татарских полков. Татарских полков было на два больше, чем русских. Число татарских полков разбитых после битвы на 5 больше, чем русских, а всего было разбито 11 полков. Сколько полков уцелело после битвы с каждой стороны отдельно?
4 русских полка; 1 татарский полк.
545. Бутылка с маслом весит 900 г. Масло на 100 г тяжелее бутылки. Сколько весит масло?
500 г.
546. Разница между двумя числами равна 87. Если разделить первое число на второе, то получится неполное частное 11 и остаток 7. Найти эти числа.
95; 8.
547. Если Алена купит одну конфету, то у нее останется 10 копеек, а на 2 конфеты у нее не хватает 30 копеек. Сколько стоит конфета?
40 копеек.
548. Банка с медом весит 500 г. Та же банка с керосином весит 350 г. Керосин легче меда в 2 раза. Сколько весит пустая банка?
200 г.
549. Крестьянин хочет купить лошадь и для этого продает рожь. Если он продаст 15 ц ржи, то ему не хватит для покупки лошади 80 руб., а если он продаст 20 ц ржи, то после покупки у него останется 150 руб. Сколько стоит лошадь?
770 руб.
550. В коробке лежали синие, красные и черные карандаши – всего 60 штук. Красных карандашей было на 4 меньше, чем черных, и на 8 меньше, чем синих. Сколько красных карандашей было в коробке?
^ 16 красных карандашей.
551. Масса африканского слона в 2 раза больше массы бегемота. А масса самого крупного на земле животного - синего кита в 12 раз больше, чем масса бегемота и слона вместе взятого. Определите массу каждого животного в отдельности, если все три вместе весят 156 тонн.
^ 4 т – масса бегемота; 8 т – масса африканского слона; 144 т – масса синего кита.
552. Трем коммерческим организациям была распределена клубника, собранная с одного участка прямоугольной формы периметром 200 м, ширина которого в 3 раза меньше его длины. В среднем с 1 м2 собрали по 6 кг клубники. По сколько килограммов клубники получила каждая коммерческая организация, если известно, что полученная масса выражается тремя последующими числами натурального ряда?
3749 кг; 3750 кг; 3751 кг.
553. Если количество карандашей находящихся в коробке увеличить вдвое, то до полной коробки не хватит 2-х карандашей. Если то же количество карандашей увеличить втрое, то 3 карандаша не поместятся в коробке. На какое количество карандашей рассчитана коробка?
12 карандашей.
554. Спортивная площадка прямоугольной формы имеет периметр 420 м. Ее длина в 2 раза больше ширины. Площадь разделена на две части так, что одна часть на 450 м2 больше другой. Какова площадь каждой части?
4675 м2; 5125 м2.
555. Четыре участка заняты зерновыми культурами. Второй участок в 2 раза больше первого, площадь третьего участка равна сумме площадей первого и второго участков, а площадь четвертого участка – сумма площадей первых трех участков. Определить площадь каждого участка, если всего собрано 14 976 ц зерна при среднем урожае 26 ц с гектара.
48 га; 96 га; 144 га; 288 га.
556. В нашем классе 15 двухместных парт. Одна парта пустует. Сколько девочек и сколько мальчиков в классе, если количество девочек в 3 раза больше, чем количество мальчиков?
21 девочка; 7 мальчиков.
557. Который теперь час, если оставшаяся часть суток в 5 раз больше прошедшей части?
4 часа.
558. Который теперь час, если через два часа до конца суток останется в три раза больше, чем уже пройдет?
^ Сейчас 4 часа.
559. На двух смежных станциях вместе было 120 вагонов. После того, как с первой станции на вторую перешел состав в 30 вагонов, а со второй станции на первую перешел состав в 20 вагонов, на первой станции стало вагонов столько же, сколько и на второй. Сколько вагонов было на каждой станции первоначально?
I ст. – 70 ваг.; II ст. – 50 ваг.
560. Длина прямоугольного участка в 4 раза больше его ширины, причем ширина на 600 м меньше длины. Сколько риса получено с участка, если с каждого гектара получено по 35 ц риса?
560 ц риса.
561. На шапке царя Ивана Грозного было 24 драгоценных камня. Алмазов было в 8 раз больше, чем изумрудов и на 7 меньше, чем сапфиров. Сколько алмазов, изумрудов и сапфиров в отдельности было на шапке у Ивана Грозного?
^ 8 алмазов; 1 изумруд; 15 сапфиров.
562. Мать разделила поровну мандарины между 3-мя детьми. Когда каждый из них съел по 4 мандарина, у них осталось вместе столько мандаринов, сколько получил каждый. По сколько мандаринов досталось каждому?
^ По 6 мандаринов.
563. Как-то рано по утру
Птицы плавали в пруду.
Белоснежных лебедей
Втрое больше, чем гусей.
Уток было восемь пар –
Вдвое больше, чем гагар
Сколько было птиц всего,
Если нам еще дано,
Что всех уток и гусей
Столько, сколько лебедей. 56 птиц.
5
64. Белуга может прожить столько, сколько щука, да еще 20 лет, щука может прожить столько, сколько сом, да еще 20 лет, а сом в два раза больше золотой рыбки. Сколько лет могут прожить белуга и золотая рыбка в отдельности, если первая может прожить больше золотой рыбки в три раза да еще 10 лет?10
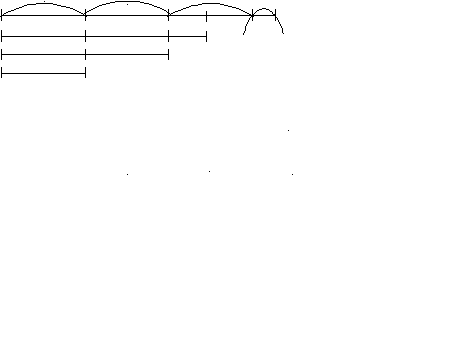
Б.
Щ. 20
С. 20
З.Р.
^ Белуга – 100 лет; золотая рыбка – 30 лет.
5
65. Яблоки двух сортов – красные и желтые разложили в две вазы – высокую и низкую. В высокой вазе красных яблок оказалось на 7 больше, чем желтых. В низкой вазе красных яблок на 5 меньше, чем желтых, а желтых на 20 больше, чем красных в высокой вазе. Каких яблок больше красных или желтых и на сколько?
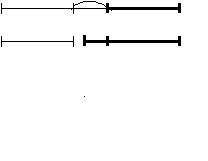К. 7Ж.
5
^ Красных яблок на 2 больше, чем желтых.
566. В один магазин для продажи привезли 1800 кг овощей: картошку, помидоры и капусту. В первый день продали десятую часть всех овощей. А во второй день на каждый кг помидор продавались 2 кг капусты и 3 кг картошки. Сколько килограммов помидор, капусты и картошки было продано во второй день?
^ 270 кг помидор; 540 кг капусты; 810 кг картошки.
567. Три рыбака поймали 96 ершей. Один из рыбаков был шутником. Он из котелка первого рыбака переложил в котелок другого 3 ерша, а потом из котелка второго рыбака в свой одного ерша. После подсчета оказалось, что у всех рыбаков стало ершей поровну. Сколько ершей поймал каждый рыбак?
35; 30; 31.
568. Скорость теплохода по течению реки равна 18 км/ч, а против течения реки – 12 км/ч. Найти скорость течения реки.
3 км/час.
569. Теплоход по течению реки проходит на 6 км/ч больше, чем против течения. Какова скорость течения реки?
3 км/час.
570. В двух кусках одинаковое количество ткани. Когда от первого куска отрезали 8 м, а от другого 18 м, в первом куске осталось в 3 раза больше ткани, чем во втором. Сколько метров ткани осталось в каждом куске?
15 м; 5 м.
571. Старинная задача. Спросил некто учителя: «Скажи, сколько у тебя в классе учеников, так как хочу отдать к тебе в ученики своего сына». Учитель ответил: «Если придет еще учеников столько же, сколько я имею, и пол столько и четверть столько и твой сын, то будет у меня учеников 100». Спрашивается, сколько учеников в классе?
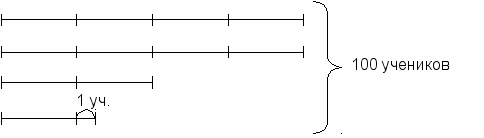
^ Ответ: 36 учеников.
572.. Старинная задача. У пятерых крестьян – Ивана, Петра, Якова, Михаила и Герасима было 10 овец. Не могли они найти пастуха, чтобы пасти овец, и говорит Иван остальным: «Будем, братцы, пасти овец по очереди: по столько дней, сколько каждый из нас имеет овец». Поскольку дней должен каждый крестьянин пасти овец, если известно, что у Ивана в два раза меньше овец, чем у Петра, у Якова в два раза меньше, чем у Ивана. Михаил имеет овец в два раза больше, чем Яков, а Герасим – вчетверо меньше, чем Петр?
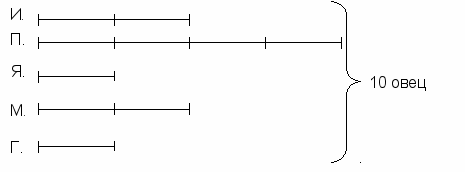
^ Иван – 2 дня; Пётр – 4 дня; Яков – 1 день; Михаил – 2 дня; Герасим – 1 день.
573. Старинная задача. Говорит дед внукам. «Вот вам 130 орехов. Разделите их на две части так, чтобы меньшая часть, увеличенная в 4 раза равнялась бы большей части, уменьшенной в 3 раза». Как разделить орехи?
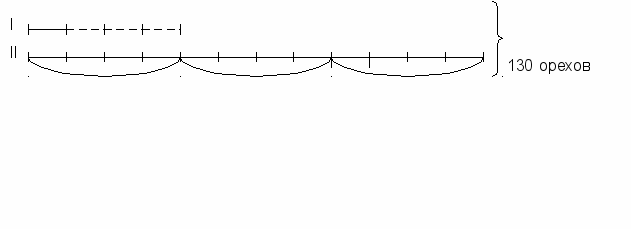
10; 120.
574. Старинная задача. Двое ели сливы. Один сказал другому: «Дай мне свои две сливы, тогда у нас слив будет поровну». На что другой ответил: «Нет, лучше ты мне отдай свои две сливы, – тогда у меня будет в два раза больше, чем у тебя». Сколько слив было у каждого?
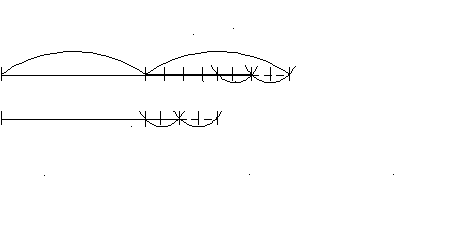
2 2
2 2
^ У одного 14 слив, у другого 10 слив.
575. Старинная задача. Прохожий, догнавший другого спросил: «Как далеко до деревни, которая у нас впереди?». Ответил другой прохожий: «Расстояние от той деревни, от которой ты идешь, равно третьей части всего расстояния между деревнями, а если пройдешь 2 версты (верста – старинная русская мера длины, 1 верста =1,067 км), тогда будешь ровно посередине между деревнями». Сколько верст осталось еще идти первому прохожему и какое расстояние между деревнями?
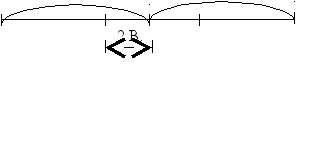
^ Ответ: 8 вёрст.
576. Старинная задача. Из четырех пожертвователей, второй отдал денег вдвое больше первого, третий втрое больше второго, а четвертый в четыре раза больше третьего. Все вместе дали 132 руб. Сколько денег дал первый?
^ Ответ: первый дал 4 рубля.
577. На детской площадке 8 двух- и трехколесных велосипедов. Всего колес у них 21. Сколько двух и трехколесных велосипедов на детской площадке?
Для решения этой задачи обозначим 8 велосипедов треугольниками.
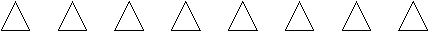
^ А теперь дорисуем колеса в виде кружочков. Мы знаем, что любой детский велосипед имеет не менее 2-х колес. Дорисуем каждому треугольнику по 2 кружочка.
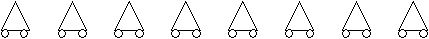
Мы использовали 2 · 8 = 16 (колес) и у нас осталось 21 – 16 = 5(колес). Как их расположить? Каждый велосипед уже имеет по 2 колеса. Дорисуем по одному колесу начиная с первого велосипеда, пока не закончим оставшиеся 5 колес, таким образом, находим число трехколесных велосипедов. Остальные велосипеды двухколесные.
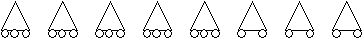
^ Проверка. 3 · 5 + 2 · 3 = 21(колесо)
2 способ. Предположим, что все 8 велосипедов – 3-х колесные, тогда должно быть 8 · 3 = 24 колеса, но их 21 колесо. Почему получилось на 3 колеса больше? Потому что каждому двухколесному велосипеду тоже добавили по 1 колесу. Следовательно, 2-х колесных велосипедов было 3, а трехколесных 8 – 3 = 5 велосипедов.
578. В зоопарке было 8 голов львов и страусов. Ног у них было всего 26. Сколько в зоопарке львов и сколько страусов?
5 львов и 3 страуса.
579. Папа купил 6 пакетов пшеничной и кукурузной муки. Масса всей муки составляет 10 кг. Сколько папа купил пакетов с кукурузной мукой и сколько с пшеничной, если масса одного пакета с кукурузной мукой равняется 1 кг, а масса одного пакета с пшеничной мукой равна 2 кг?
^ 2 пакета с кукурузной мукой и 4 пакета с пшеничной мукой
.580. Играли в прятки белки и дятлы. Из-под кустов выглядывают 12 носов и 34 лапки. Сколько их играло в прятки?
5 белок и 7 дятлов.
581. У 30 штук 3-х ножных табуреток и стульев 100 ножек. Сколько табуреток и сколько стульев, если у каждого стула по 4 ножки?
^ 10 стульев и 20 табуреток.
582. На выставку привезли 9 чайных сервизов. Всего в них было 84 чашки. Сколько было сервизов на 6 человек и сколько на 12 человек?
^ 5 сервизов на 12 человек и 4 сервиза на 6 человек.
583. В клетку посажены кролики и фазаны. У них вместе 35 голов и 94 ноги. Сколько было кроликов и сколько фазанов?
^ Мы знаем, что у кроликов 4 ноги, а у фазанов – 2. Обозначим 35 голов (т.е. общее число кроликов и фазанов) при помощи кружков.
35
^ Теперь дорисуем каждому кружочку по 2 палочки (ноги).
Всего используем: 2 · 35 = 70 (ног)
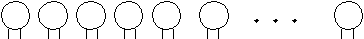
Осталось 94 – 70 = 24 (ноги), которые мы не дорисовали. Дорисуем по 2 ноги второму и т.д. до тех пор, пока не закончим те 24 «ноги», которые обозначают число кроликов с четырьмя ногами.
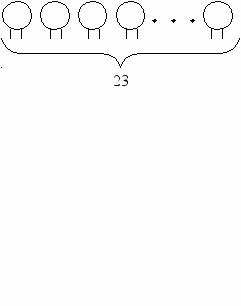
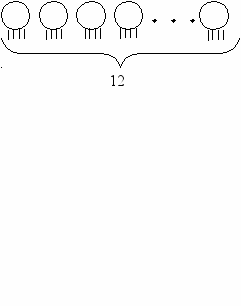
^ 24 : 2 = 12 – это число кроликов, а остальные
35 – 12 = 23 – фазаны.
Проверка: 12 + 23 = 35 (кролики и фазаны)
4 · 12 + 2 · 23 = 94 (ноги).
2 способ. Предположим, что все 35 голов являются кроликами, тогда они имели бы 35 · 4 = 140 ног, т.е. на 140 – 94 = 46 ног больше, чем было на самом деле. Почему получились лишние ноги? Потому, что всех фазанов посчитали как кроликов добавив каждому еще по 2 ноги. То есть было 46 : 2 = 23 фазана, а остальные 35 – 23 = 12 – кролики.
584. Цирковой артист на одноколесном велосипеде следил за президентским кортежем, который двигался по городу. Всего насчитали 45 колес. Сколько было автомобилей и сколько мотоциклов, если транспортных единиц было 16 да еще цирковой артист на одноколесном велосипеде?
^ 6 автомобилей и 10 мотоциклов.
585. Настасья Петровна из сказки Л.Н. Толстого «Три медведя» приготовила на десерт землянику и чернику. Земляники оказалось в 3 раза больше, чем черники. Когда каждый взял по одной землянике и одной чернике, в вазе осталось земляники в 4 раза больше, чем черники. Сколько было первоначально в вазе земляники и сколько черники?
Так как первоначально земляники было в 3 раза больше, чем черники, значит, каждой чернике соответствуют 3 земляники. Обозначим квадратом землянику, а кругом – чернику и составим группы:
Т
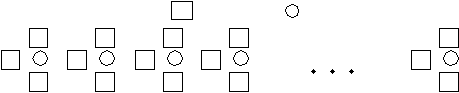ак как первоначально земляники было в 3 раза больше, чем черники, значит, каждой чернике соответствуют 3 земляники. Обозначим – землянику, а – чернику и составим группы:^ Все три медведя взяли по одной землянике и одной чернике. Покажем это на схеме, вычеркивая их из нее.
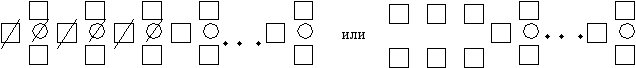
Во второй части условия задачи говорится, что когда каждый из 3-х медведей взял по одной землянике и одной чернике в вазе осталось земляники в 4 раза больше, чем черники, т.е. каждой чернике соответствует по 4 земляники. Чтобы это осуществить, к каждой чернике добавляем по одной из оставшихся 6 земляник. Очевидно, что таких групп получится 6.
После того, как каждый медведь взял по одной землянике и одной чернике, в вазе осталось 6 черник и 24 земляники.
А первоначально черники было 6 + 3 = 9 и земляники 24 + 3 = 27.
Проверка: 27 : 9 = 3 (раза) – больше земляники, чем черники.
586. У одного селянина число кур в 4 раза больше, чем число уток. Продав 5 кур и купив 3-х уток, общее число кур стало в 3 раза больше, чем число уток. Сколько кур и сколько уток было первоначально?
^ 14 уток; 56 кур.
587. В одной столовой посчитали, что если из имеющейся муки расходовать по 8 кг каждый день, тогда 4 кг не хватит, а если расходовать по 7 кг, то останется 12 кг муки. Сколько килограммов муки в столовой и на сколько дней она была рассчитана?
^ 124 кг муки; 16 дней.
588. Если посадить всех учеников данного класса по одному за партой, то останутся 6 учеников без мест, а если посадить по два ученика за 1 парту, то останутся свободными 4 парты и за одной партой будет сидеть один ученик. Сколько учеников и сколько парт было в классе?
^ Обозначим ученика буквой «У», а парту буквой «П». «Посадим» за каждую парту по одному ученику и получим следующие группы:
У У У … У
П П П … П и 6 учеников
Но если посадить за парту по 2 ученика, получим:
У У У … У У У У … У
П П П … П П П П … П
У У У … У
Но, из второй части задания, когда рассаживаем учащихся по двое за парту, то 4 парты остаются свободными, и за одной партой будет сидеть один ученик. Поднимем с тех парт, где сидят по одному – 4-х учеников, и освободим 4 парты, а их рассадим на другие парты, где сидят по одному ученику. Тогда получим следующую схему:
У У У У У У У У
П
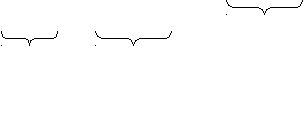П П П П П П П П П П ПУ У У У У У У 4 1
6 4
Всего в классе находятся 6 + 4 + 4 + 1 = 15 (парт), а учеников 1 · 15 + 6 = 21.
589. Если пришить на каждое пальто по 4 пуговицы, то останется 3 пуговицы. Если пришить по 5 пуговиц на эти же пальто, то на одном пальто будет только 3 пуговицы. Сколько всего было пальто и пуговиц?
5 пальто и 23 пуговицы.
590. Украшали новогоднюю елку. Если на каждую ветку повесить по 3 игрушки, то 2 игрушки останутся, а если на каждую ветку повесить по 4, то 9 игрушек не хватит. Сколько веток на елке, сколько новогодних игрушек?
^ 11 веток; 35 игрушек.
591. После окончания концерта, 174 зрителя пошли пешком, остальные поехали на электричке, заняв 18 вагонов. В каждый вагон сели на 8 человек больше, чем посадочных мест. Если зрители, уехавшие на электричке, занимали бы только места на скамейках, то потребовалось бы еще 3 вагона и в последнем вагоне осталось бы 6 свободных мест. Найти общее число зрителей.
1218 зрителей.
592. Если в каждую байдарку посадить по 2 спортсмена, то на берегу останутся 3 спортсмена. А если в каждую байдарку посадить по 3 спортсмена, то не хватит 2-х спортсменов, чтобы полностью загрузить все байдарки. Сколько было спортсменов и сколько байдарок?
Делая анализ задачи, выясним, что в задаче говорится о спортсменах и байдарках. Обозначим спортсменов кружками, а байдарки – прямоугольниками. Из первой части задачи нам известно, что если посадить в каждую байдарку по 2 спортсмена, то 3 спортсмена останутся на берегу, без места. Представим это при помощи следующего рисунка:
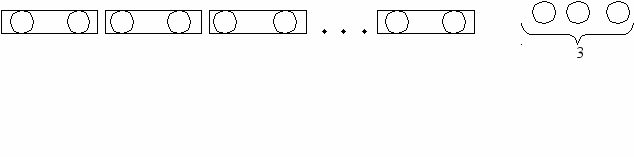
Вторая часть условия задачи говорит о том, что если сделать перегруппировку, т.е. в каждую байдарку посадить по 3 спортсмена, то не хватит 2-х спортсменов, чтобы в каждой байдарке стало по 3 спортсмена. Постараемся это показать схематически. Можно сделать другой рисунок, где в каждом прямоугольнике нарисовано по 3 спортсмена (кружочка), а в последнем прямоугольнике один кружочек, т.к. не хватает 2-х спортсменов, чтобы во всех байдарках было по 3 спортсмена. Но тогда непонятно, как же мы найдем ответ на вопрос задачи? А может быть можно сделать по-другому? Давайте вернемся к рисунку, где в каждой байдарке сидят по 2 спортсмена, а 3 остались на берегу. Оставшихся 3 спортсменов рассадим к остальным по одному в каждую байдарку. Тремя спортсменами будут заняты 3 байдарки.
Так как двух спортсменов не хватает, чтобы в каждой байдарке было по 3 спортсмена, в двух байдарках сидят по двое. Отсюда можно сделать вывод: в трех байдарках по 3 спортсмена, в двух байдарках – по 2 спортсмена, т.е. число байдарок было 3 + 2 = 5, а спортсменов 3 · 3 + 2 · 2 = 13.
^ Проверка: 2 · 5 = 10 (спортсменов) – если посадить по 2 в байдарки, 13-10=3(спортсмена) – останутся на берегу.
593. В доме мама раскладывала на окна цветы. Если на окно поставить по 3 цветка, то 2 цветка останутся, а если по 4 – то одно окно останется без цветков. Сколько цветков и сколько окон в доме?
^ 6 окон; 20 цветков.
594. В стопке было в 4 раза больше тетрадей по математике, чем по русскому языку. Если добавить 2 тетради по русскому языку и забрать 4 тетради по математике, то тетрадей по математике будут в два раза больше, чем по русскому языку. Сколько тетрадей по математике и по русскому языку было первоначально?
^ 4 тетради по русскому языку и 16 тетрадей по математике.
595. «Палки и галки» (народная задача)