Рецензенты: И. Б. Левицкая проректор по научной работе гоу «Государственный институт развития образования», к п. н., доцент

Вид материала

Книга

Содержание Володя – 1 место 12 · 2 = 24 (мм) – две длины второго прямоугольника 48 : 16 = 3 (мм) – ширина первого прямоугольника Ii вариант 1 км =1000 м – дистанция Миши. 36 : 4 = 9 (см) – сторона квадрата. 10 · 8 = 80 (см) – площадь прямоугольника. Городской или районный тур 175 рублей 20 копеек. Может, это квадрат со стороной 3 ед. Буратино обманул 4 раза. Лесничий прав, так как количество зверей должно быть числом натуральным. Тестовые задания

Подобный материал:

• Н. А. Добролюбова, проректор по научной работе, 50.95kb.
• Учебно-методическое пособие удк 796/799 (075. 8) Печатается по решению ббк 74. 267., 3134.91kb.
• «Использование потенциала семьи в системе коррекционного воздействия на ребёнка», 138.16kb.
• Русские в Турции. 1920-1921, 352.95kb.
• Содержание подготовки методистов-организаторов в системе повышения квалификации работников, 284.53kb.
• Ильина Нина Федоровна,, 93.42kb.
• А. А. Левицкая, кандидат педагогических наук, доцент, 158.25kb.
• Тезисы выступления, 2699.95kb.
• Программа Челябинск 2011 г. Министерство образования науки Российской Федерации Южно-Уральский, 580.08kb.
• С. Х. Мухаметгалиева Елабуга, Елабужский государственный педагогический университет, 3598.14kb.

5. Володя пробежал 400 м за 1 мин 25 сек, Коля – за 125 сек, а Петя бежал со скоростью 4 м/с. Кто из них занял I, II, III место?

^ Володя – 1 место;

Петя – 2 место;

Коля – 3 место.

6. Какие уравнения имеют одинаковые корни? Найдите их.

а) 38 · 7 + х = 1 066;

б) 37 · 8 + х = 1 066;

в) х + 38 · 7 = 1 000 + 66.

Одинаковые корни имеют уравнения а) и в).

38 · 7 + х = 1 066; х = 800;

х + 38 · 7 = 1 000 + 66; х = 800.

7. Два прямоугольника имеют одинаковую площадь. Длина первого – 16 мм, второго – 12 мм. Найдите ширину первого прямоугольника, если периметр второго равен 32 мм.

^ 12 · 2 = 24 (мм) – две длины второго прямоугольника;

32 – 24 = 8 (мм) – две ширины второго прямоугольника;

8 : 2 = 4 (мм) – ширина второго прямоугольника;

12 · 4 = 48 (мм) – площадь каждого прямоугольника;

^ 48 : 16 = 3 (мм) – ширина первого прямоугольника.

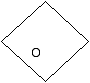
8. Площадь, какой фигуры больше: круга, радиус которого 3 см или квадрата, диагональ которого 6 см?

В


А С

Ответ:


D

Наложением фигур определяем: S _круга > S _{квадрата.}

АС = 6 см; ОС = 3 см.


^

II ВАРИАНТ

1. Определите, по какому правилу записаны числа в столбике, и, если возможно, дополните его:
   

349 200

394 200

439 200

493 200

По принципу использования одинаковых цифр в разряде сотен, тысяч, десятков тысяч и единиц тысяч: 349 200, 394 200, 439 200, 493 200, 934 200, 943 200.

2. Выберите выражение, соответствующее данному условию, и вычислите его значение: частное двух чисел уменьшили на несколько единиц и полученный результат увеличили в несколько раз.

а) (72 : 8 + 3) · (15 – 6); 9 6 9

б) 72 : 8 – 3 · 15 – 6; Ответ: (72 : 8 – 3) · (15 – 6) = 54

в) (72 : 8 – 3) · (15 – 6).

2. Вставьте пропущенные числа. Какие из них могут иметь несколько значений?
   

( ) · = 72 Ответ: ( ) · = 72

9 15 6

9 0

54 27 18

4. Вместо точек поставьте соответствующие единицы измерения:

а) масса батона 500 …;

б) расстояние между селами 5 … ;

в) площадь комнаты 20 … .

а) 500 г;

б) 5 км;

в) 20м².

5. Костя пробежал 100 м за 18 сек, а Миша пробежал 1 км за 2 мин 30 сек. Кто из мальчиков бегает быстрее?

^ 1 км =1000 м – дистанция Миши.

1000 : 100 = 10 (раз).

2 мин 30 сек = 120 сек + 30 сек = 150 сек – время Миши.

18 · 10 = 180 (сек) – время Кости на дистанции 1 км.

150 сек < 180 сек.

Скорость Миши больше, значит, Миша бегает быстрее.

6. Какие уравнения имеют одинаковые корни? Найдите их.
   

а) 46 · 8 + у = 868;

б) у + 46 · 8 = 860 + 8;

в) у + 48 · 6 = 860 + 8.

Одинаковые корни имеют уравнения а) и б).

46 · 8 + у = 868; у = 500;

у + 46 · 8 = 860 + 8; у = 500.

6. Квадрат и прямоугольник имеют одинаковый периметр – 36 см. Площадь, какой фигуры больше, если длина прямоугольника 10 см?
   

^ 36 : 4 = 9 (см) – сторона квадрата.

9 · 9 = 81 (см²) – площадь квадрата.

36 : 2 = 18 (см) – сумма двух сторон прямоугольника.

18 – 10 = 8 (см) – сторона прямоугольника.

^ 10 · 8 = 80 (см²) – площадь прямоугольника.

S _{квадрата >}S _{прямоугольника}

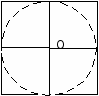
6. Площадь какой фигуры больше: круга, диаметр которого 8 см или квадрата, сторона которого 8 см.
   

Наложением фигур определяем: S _круга < S _{квадрата}

В С



М Р


А D

^

ГОРОДСКОЙ ИЛИ РАЙОННЫЙ ТУР

1. Старинная задача. Если одна лошадь на 10 верст пути стоит 15 копеек, то, сколько должны заплатить за 16 лошадей на 730 верст пути?

^ 175 рублей 20 копеек.

2. Один человек решил проверить, насколько сообразительны его трое сыновей. Взяв три шапки, каждая из которых была белая или черная, он велел сыновьям закрыть глаза, надел каждому на голову шапку, и спросил: « Как, видя цвет шапок своих братьев, отгадать цвет своей шапки?» Как сыновья пришли к верному решению?

Так как каждого цвета была, по крайней мере, одна шапка, то их могло быть две белые и одна черная или одна белая и две черные. Поэтому один из братьев, видя, что цвет шапок у двух других братьев одинаковый – белый (черный), мог сказать, что он знает цвет своей шапки. Другой брат, видя, что на братьях шапки белого и черного цветов и один брат сказал какого цвета его шапка – черного (белого) цвета, может сделать вывод, что на нем белая (черная) шапка. То же самое может сказать и третий брат.

3. Задумано трехзначное число, у которого с любым из трех чисел 543, 142 и 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?

163.

4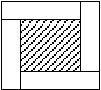. Квадрат со стороной 7 ед., разбит на 5 прямоугольников, как изображено на рисунке (рис.1). Известно, что площадь прямоугольников, прилежащих к границе заштрихованного прямоугольника, равна 10 кв. ед. Длины сторон всех прямоугольников выражены целыми числами. Может ли заштрихованный прямоугольник быть квадратом?


Рис. 1


^ Может, это квадрат со стороной 3 ед.


5. Рост Буратино 1 м 4 дм, а длина его носа раньше была 9 см. Каждый раз, когда Буратино обманывал, длина его носа удваивалась. Как только длина его носа стала больше его роста, Буратино перестал обманывать. Сколько раз он обманул?

^ Буратино обманул 4 раза.

6. Таблицу нужно заполнить, используя числа 1, 2, 3, 4, 5 так, чтобы каждое число появилось в каждом столбике, каждой строчке и каждой диагонали ровно по одному разу. Первые несколько чисел уже расставлены. Какое число будет в центральной клетке?




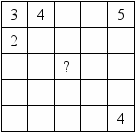
В левом нижнем углу не может стоять 2, 3, 4, 5, так как каждое число должно быть написано в каждой строчке, в каждом столбце и в каждой диагонали по одному разу. Поэтому там записано число 1. В центральной клетке не могут стоять числа 1, 3, 4, 5. Следовательно, там записано число 2.

7. Сын лесничего помогал отцу вести подсчет зверей в лесу. После подсчета он сказал отцу: «Я считал белок, зайцев и оленей. Всего зверей 1000, зайцев на 250 больше, чем оленей, белок на 300 больше, чем зайцев». Услышав такой ответ, лесничий сказал, что такого быть не может. Прав ли лесничий?

^ Лесничий прав, так как количество зверей должно быть числом натуральным.

8. Коля заметил, что во время липового медосбора пчела вылетает из улья со скоростью 4 м/с и возвращается обратно через 7 мин со скоростью 2 м/сек. На каком расстоянии от улья расположена липа, с которой пчела взяла мед, если на сбор меда с липы во время одного полета пчела затрачивает 1 мин?

Время полета составляет 7 – 1 = 6 мин. Так как пчела без меда летит вдвое быстрее, то времени на полет без меда потребуется вдвое больше, т.е. одну часть времени пчела тратит на полет туда и две части на обратный полет. Получается, что до липы пчела летит 6 : 3 = 2 (мин) = 120 (с). Расстояние между ульем и липой составляет 4 · 120 = 480 (м).


^

ТЕСТОВЫЕ ЗАДАНИЯ