Рецензенты: И. Б. Левицкая проректор по научной работе гоу «Государственный институт развития образования», к п. н., доцент
| Вид материала | Книга |
- Н. А. Добролюбова, проректор по научной работе, 50.95kb.
- Учебно-методическое пособие удк 796/799 (075. 8) Печатается по решению ббк 74. 267., 3134.91kb.
- «Использование потенциала семьи в системе коррекционного воздействия на ребёнка», 138.16kb.
- Русские в Турции. 1920-1921, 352.95kb.
- Содержание подготовки методистов-организаторов в системе повышения квалификации работников, 284.53kb.
- Ильина Нина Федоровна,, 93.42kb.
- А. А. Левицкая, кандидат педагогических наук, доцент, 158.25kb.
- Тезисы выступления, 2699.95kb.
- Программа Челябинск 2011 г. Министерство образования науки Российской Федерации Южно-Уральский, 580.08kb.
- С. Х. Мухаметгалиева Елабуга, Елабужский государственный педагогический университет, 3598.14kb.
ОЛИМПИАДНЫЕ ЗАДАНИЯ ПО МАТЕМАТИКЕ
В 4-х КЛАССАХ
(2005 / 06 УЧЕБНЫЙ ГОД)
МОУ «ТИРАСПОЛЬСКАЯ СРЕДНЯЯ ШКОЛА № 17 им. В.Ф. РАЕВСКОГО»
^ ШКОЛЬНЫЙ ТУР
Восстанови числовые выражения.
х* * 5 _9 0 * * 0 *
 4 * * 7 6 5 * 3
4 * * 7 6 5 * 33 * * * 0 4 5 7
2 * *
1 * * * *
2 б.
2. Поставь скобки, чтобы равенства были верные. Напиши промежуточные ответы.
5206 – 180 : 6 · 10 = 4906
720 – 480 : 6 + 530 = 570
2 б.
3. Запиши уравнение, где сумма чисел равна 50 000, второе слагаемое – наименьшее шестизначное число, записанное разными числами, кроме 0. Найди первое слагаемое.
3 б.
4. Какая величина лишняя в каждой строке?
5 м 7 см 570 см 57 дм 5 м 50 см
7214 км 4073 дм 6507 кг 2800 м
2 б.
5. Найди периметр прямоугольника, если его площадь равна площади квадрата, периметр которого 240 м, а длина этого прямоугольника в 2 раза больше стороны квадрата.
8 б.
6. Стол и тумбочка стоят 680 рублей. Три стола и две тумбочки стоят 1840 рублей. Найди цену 1 стола, а также одной тумбочки.
8 б.
7. Три курицы за три дня снесли 3 яйца. Сколько яиц снесут 12 кур за 12 дней, если они будут нести такое же одинаковое количество яиц за один и тот же промежуток времени?
10 б.
8. Малыш может съесть 600 г варенья за 6 мин, а Карлсон в 2 раза быстрее. За какое время они съедят это варенье вместе?
8 б.
Приложение 5
^
ОЛИМПИАДНАЯ РАБОТА
ПО МАТЕМАТИКЕ (2000 / 01 УЧЕБНЫЙ ГОД) ДЛЯ
НАЧАЛЬНЫХ КЛАССОВ
(ТИРАСПОЛЬСКОЕ УНО)
III тур
1. Трехзначное число записано разными цифрами в порядке увеличения их значений, но в его названии все слова начинаются с одной буквы.
Другое трехзначное число состоит из одинаковых цифр, а в его названии все слова начинаются с разных букв.
Какие это числа?
- Знайка перемножил все целые числа до 200 включительно. Сколько цифр у него получилось в значении произведения?
- На первом поле работало на 12 на человек больше, чем на втором. На сколько больше человек будет работать на первом поле, если со второго уйдут 2 человека?
- Улитка с седьмой страницы книги переползла на двадцатую страницу. Через сколько листов пришлось переползти улитке, если она на каждой странице побывала 1 раз?
- На реке один рыбак поймал 3 щуки, второй 16 – карасей, а третий 40 – пескарей. Чей улов тяжелее, если 1 щука весит столько же, сколько 5 карасей или 13 пескарей?
- В ящике лежало 64 кубика. Пятеро мальчиков договорились брать из него по очереди по половине имеющихся в нем кубиков. Первый взял половину кубиков от 64, второй половину оставшихся там кубиков и т. д.
Сколько кубиков взял каждый мальчик?
7. Найди значение выражения:
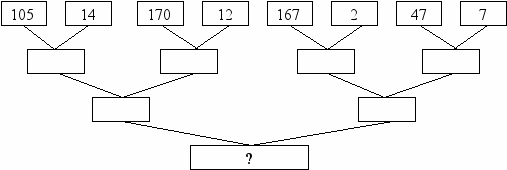
+ -
:
Приложение 6
^ ОЛИМПИАДНЫЕ ЗАДАНИЯ ПО МАТЕМАТИКЕ ДЛЯ УЧАЩИХСЯ
4 - х КЛАССОВ
(2006 г., РЫБНИЦКОЕ УНО)
РАЙОННЫЙ И ГОРОДСКОЙ ТУР
Задачи, оцениваемые в 3 балла.
1. В этом году ежегодный конкурс «Кенгуру» проводится в России уже в 13 раз. В каком году был первый конкурс?
а) 1993 г; б) 1994 г; в) 1894 г; г) 1994 г.
2. Общий вес троих детей 72 кг. Маша весит столько же, сколько два её младших брата вместе. Сколько весит Маша?
а) 18 кг; б) 24 кг; в) 32 кг; г) 36 кг; д) 52 кг.
- Вместо ? знака напишите необходимое число:
420 : х : 10 14
56 : 2 : х ?
а) 5; б) 8; в) 6; г) 7; д) 9; е)10.
4. В магазин привезли 4 полные одинаковые коробки. В одной – апельсины, в другой – мандарины, в четвёртой – вишни. В какой коробке наибольшее число плодов?
а) в коробке с апельсинами; б) в коробке с яблоками;
в) в коробке с мандаринами; г) в коробке с вишнями;
д) невозможно определить.
 5. Цапля села на записанное в тетради верное равенство. Какое число она закрыла?
5. Цапля села на записанное в тетради верное равенство. Какое число она закрыла? 6400 – 2396 = – 3496
а) 5900; б) 6000; в) 6200; г) 4004; д) 7500.
6. Какое число обладает такими свойствами: оно чётное, все его цифры различны, а число сотен в 2 раза больше числа единиц?
а) 1236; б) 3478; в) 4683; г) 4874; д) 8462.
7. Квадрат разрезали на 3 кусочка. Два из них изображены на рисунке справа. Укажите третий кусочек
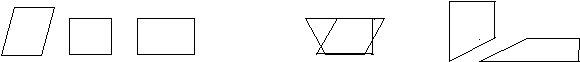
а) б) в) г) д)
8. В летнем лагере «Кенгуру» Алёша решал по 6 задач в день, а Андрей – по 3 задачи. Алёша решил все задачи за 5 дней. За сколько дней решил эти же задачи Андрей?
а) 4; б) 5; в) 6; г) 8; д) 10.
9. Денис живёт в своем доме вместе с папой, мамой, братом, дедушкой и бабушкой. А ещё с ними живут собака, кошка, 3 канарейки и 6 золотых рыбок. Сколько всего ног у обитателей этого дома?
а) 22; б) 26; в) 28; г)24; д) 30; е) 20.
10. Если одно из чисел увеличить в 10 раз, а другое уменьшить в 5 раз, то произведение этих чисел …
а) увеличится в 2 раза; б) уменьшится в 2 раза;
в) увеличится в 20 раз; г) уменьшится в 5 раз;
е) не изменится.
Задачи, оцениваемые в 4 балла.
11. В ящике лежало 64 кубика. Пятеро мальчиков договорились брать из него по очереди по половине имеющихся в нём кубиков. Первый берет половину всех кубиков, второй – половину оставшихся и так далее. Сколько кубиков возьмёт пятый мальчик?
а) 3; б) 4; в) 2; г) 5; д) 1; е) 0.
12. Галя записала числа по порядку от 1 до 99. Сколько раз Галя написала цифру 6?
а) 10; б) 12; в) 15; г) 20; д) 25; е) 30.
13. У Даши было 9 кусочков бумаги. Некоторые из них она разрезала на 3 части. Всего получилось 15 кусочков. Сколько кусочков разрезала Даша?
а) 1; б) 2; в) 3; г) 4; д) 5; е) 6.
14. Расшифруйте и запишите комбинацию кодового замка, если:
а) третья цифра на 3 больше, чем первая;
б) вторая цифра на 2 больше, чем четвёртая;
в) в сумме все цифры дают 17;
г) вторая цифра 3;
д) число четырехзначное.
15. Царь Кощей подобрел и решил потратить 50 золотых монет на подарки детям. В сундуке у него хранится 5 ларцов, в каждом ларце по 3 шкатулки, а в каждой шкатулке по 10 золотых монет. Сундук, ларцы и шкатулки заперты на замки. Какое наименьшее число замков потребуется открыть Кощею, чтобы достать 50 монет?
а) 5; б) 6; в) 7; г) 8; д) 9; е) 10.
16. У коллекционера 4000 марок. Половина всех марок – о млекопитающих, четверть – о птицах, половина оставшихся – о рыбах, а остальные – о рептилиях. Сколько марок с рептилиями у коллекционера? Запиши решение своё на листочке.
а) 1000; б) 2000; в) 500; г) 250; д) 1500.
17. В двузначном числе 7 десятков и несколько единиц. Между цифрами этого числа вписали ноль. На сколько полученное трехзначное число больше двухзначного?
а) 50; б) 60; в) 600 г) 630; д) 650; е) 700.
18. Дед Опанас был на свадьбе в соседнем селе. Туда он шёл пешком, а обратно ехал. Первую половину пути он ехал на волах, причём двигался со скоростью, вдвое меньшей, чем на пешем пути. А другую половину он ехал на коне – в 5 раз быстрее, чем шёл пешком. Какой путь занял больше времени: на свадьбу или домой?
а) на свадьбу шёл быстрее; б) домой приехал быстрее;
в) одинаково; г) невозможно определить.
19. Две девочки и три мальчика съели 16 порций мороженого. Каждый мальчик съел в 2 раза больше порций, чем каждая девочка. Сколько порций съедят 3 девочки и 2 мальчика с такими же аппетитами? (Запиши решение на листке своим).
а) 12; б) 13; в) 14; г) 16; д) 17; е) 18.
20. Вокруг прямоугольного сквера проложена дорожка, которая на всём своём протяжении имеет одинаковую ширину. Наружная граница дорожки на 8 метров длиннее внутренней. Чему равна ширина дорожки?
а) 50 см; б) 1 м; в) 2 м; г) 3 м; д) 4 м.
Задачи, оцениваемые в 5 баллов.
21. Алёна начала делать уроки в 16 ч 10 мин. Через 1 ч 55 мин к ней подошла младшая сестрёнка и попросила почитать ей сказку. Сколько времени Алёнка может потратить на чтение, если ей необходимо закончить приготовление уроков в 8 ч вечера, а ей осталось ещё сделать математику, на которую она потратит 45 минут? Запиши решение на листочке.
а) 1 ч; б) 50 мин; в) 40 мин; г) 1 ч 10 мин; д) 1 ч 30 мин; е) 2 ч.
22. В семье четверо детей. Им 5, 8, 13 и 15 лет, а зовут их Таня, Юра, Света и Лена. Одна девочка ходит в детский сад, Таня старше Юры, а сумма лет Тани и Светы делится на 3. Сколько лет Лене?
а) 5; б) ?; в) 13; г) 15;
д) невозможно определить.
23. Между некоторыми цифрами 1 2 3 4 5 поставь знаки действий и скобки так, чтобы получилось 40. Запиши решение на листочке.
24. Две бригады посадили 220 яблонь. Первая бригада сажала в день 40 яблонь, вторая – 50 яблонь. Вторая бригада начала работу на 1 день позже, чем первая. Сколько яблонь посадила первая бригада? Запиши решение на листочке.
а) 80; б) 100; в) 120; г) 140; д) 160; е) 180.
25. Купили 2 торта одинаковой толщины, прямоугольной формы. Длина и ширина одного торта в 2 раза больше, чем другого. Масса большего торта 2 кг. Какова масса меньшего торта? Начерти прямоугольники. Запиши решение на листочке.
а) 500 г; б) 1000 г; в) 1500 г.
26. Три курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 12 кур за 12 дней?
а) 6; б) 9; в) 12; г) 24; д) 30; е) 48.
27. Из глиняного кувшина кефир разделили в 4 одинаковые чашки. В кувшине осталось кефира ровно на 1 чашку. Во всех сосудах сейчас 1 кг 200 г кефира. Сколько граммов кефира помещается в 1 чашке? Запиши решение.
а) 200 г; б) 240 г; в) 250 г; г) 150 г; д) 300 г.
28. Квадрат со стороной 4 дм распилили на квадратики со стороной 1 см и выложили их в полоску толщиной 1 см. Какой длины получилась полоска? Запиши решение на листочке.
а) 10 м; б) 12 м; в) 14 м; г) 16 м; д) 18 м; е) 20 м.
29. В магазине № 5 Разве хватит здесь сапожек?
Очередь стоит опять! 15 хвостиков подряд
Покупают кошки Рядом с продавцом дрожат!
Для себя сапожки! Уточки и кошки –
Рядом с кошками стоят Все хотят сапожки!
Стайка желтеньких утят. Спрашиваем мы ребят:
46 у нас здесь ножек – Сколько кошек и утят?
Запиши решение.
Приложение 7
^ ИНТЕГРИРОВАННАЯ ОЛИМПИАДА
Задания I тура
1. Числовой биологический диктант:
- количество конечностей у человека умножить на количество конечностей у насекомых и прибавить количество звуков в слове подъём;
- от количества глаз у рыбы отними количество глаз у лягушки и умножь на количество составных частей (морфем) в слове пальто;
- к количеству лёгких у человека прибавь количество лёгких у рыбы и умножь на количество звуков [и] в предложении: ^ В густом лесу под ёлками лежит мешок с иголками;
- количество почек у человека раздели на количество его желудков, и прибавь количество согласных звуков в слове яблоневая;
- сложи все получившиеся числа и прибавь количество пальцев на ногах у человека и количество твёрдых согласных звуков в слове человек;
(За каждое правильно выполненное задание начисляется 1 балл, максимальное количество баллов – 5.)
2. На трёх участках земли высадили 57 000 кустов: на первом – 12 900 кустов, а на втором – в 4 раза больше, чем на третьем. На каждом квадратном метре высадили по 3 куста. Какую площадь занимает второй участок? По какому существенному признаку дерево отличается от кустарника? Найди и подчеркни слово, которое произошло от латинского q u a t t u o r (кваттуор).
(Математика – 3 балла, экология – 1 балл, русский язык – 1 балл, максимальное количество баллов – 5.)
3. Мышке до норки 20 шагов. Кошке до мышки 5 прыжков. Пока кошка совершит один прыжок, мышка сделает 3 шага, а один кошачий прыжок равен 10 мышиным шагам. Догонит ли кошка мышку? Назови как можно больше признаков, согласно которым мышка похожа на кошку. Определи подлежащее и сказуемое во втором предложении задачи.
(Математика - 3 балла, экология – 1 балл за каждый существенный признак, русский язык – 1 балл.)
4. Число яблок в корзине – двузначное. Яблоки можно разделить поровну между 2, 3 и 5 детьми, но нельзя разделить поровну между 4 детьми. Сколько яблок в корзине?
Составь список из трёх слов так, чтобы слово яблоко оказалось лишним, объясни свой выбор. Запиши второе предложение, заменив числа словами.
(Математика – 2 балла, экология – 3 балла, русский язык – по 1 баллу за каждое правильно написанное числительное.)
^ Задания II тура
- Волки живут стаями, а рыси и лисы – нет. Предложи объяснение такого поведения животных. Выпиши все словосочетания из первого предложения.
Вместо букв вставь в пример числа 0, 1, 2, 3, 5, 6, 7, 8. Одинаковым буквам соответствуют одинаковые числа. Букве И соответствует число 7. Какой это пример?
Р
 ЫСИ
ЫСИЛИСЫ
ВОЛКИ
(Математика – 2 балла, экология – 3 балла, русский язык – 1 балл за правильно выписанное словосочетание.)
2. В углах квадратной клумбы растут кусты – всего 4 куста. Площадь клумбы увеличили в 2 раза, не выкапывая кустов. Расширенная клумба тоже квадратная, и внутри неё кустов нет. Как это сделали? Выполни рисунок. Сколько орфограмм в слове площадь? Укажи их. Заполни таблицу так, чтобы в горизонтальных и вертикальных рядах не оказалось рядом два дерева или два кустарника.

(Математика – 1 балл, экология – 1 балл за каждое правильное расположение, русский язык – 1 балл за каждую правильно обозначенную орфограмму.)
3. Аня, Боря, Вера и Гена вместе поймали 10 рыбок, причём каждый из детей поймал разное количество рыбок. Аня поймала больше всех, а Вера меньше всех. Кто поймал больше рыбок, мальчики или девочки? Закончи фразу «Окунь – рыба, потому что…». Можно ли рыбу превратить в человека? Как?
(Математика – 2 балла, экология – 1 балл за каждый правильно названный признак, русский язык – 2 балла.)
4. Коля заметил, что во время липового медосбора пчела вылетает из улья со скоростью 4 м/с и возвращается обратно через 7 минут со скоростью 2 м/с. На каком расстоянии от улья расположена липа, с которой пчела взяла мёд? Учти, что на сбор мёда с липы во время одного полёта пчела затрачивает 1 минуту.
Найди в задаче слова, в которых разное количество звуков и букв.
В столбиках слов обведи множество всех птиц одной окружностью, а множество всех животных, умеющих летать, - другой окружностью. Кто оказался в пересечении двух окружностей?
-
Пчела
Ласточка
Пингвин
Бабочка
Воробей
Страус
Летучая
мышь
Орёл
Киви
(Математика – 2 балла, экология – 1 балл за правильно выполненное первое задание и 1 балл за правильный ответ, русский язык – 1 балл за каждое найденное слово.)
^ Задания III тура
1. В четырёх ящиках по одному лежат: груздь, боровик мухомор, и рыжик. На первом ящике надпись – «Груздь», на втором – «Рыжик или груздь», на третьем – «Мухомор или рыжик», на четвёртом – «Боровик, или рыжик, или мухомор». При этом ни одна надпись не соответствует действительности. Какой гриб лежит в каждом ящике?
Найди в задаче слово, звуковая оболочка которого может обозначить печальное настроение, запиши звуковую форму этого слова.
Обобщи одним словом: груздь, боровик, мухомор, рыжик. Исключи лишнее, объясни.
(Математика – 1 балл, экология – по 1 баллу за каждое правильно выполненное задание, русский язык – по 1 баллу за каждое правильно выполненное задание.)
2. Жила в реке большая прожорливая щука. Все рыбы её боялись. Как-то стая в 55 рыбок – плотва, окуньки и пескари – гуляла близ осоки. Щука задумала полакомиться рыбками и напала на стаю. Когда испуганные рыбки вновь собрались в стаю, то увидели, что их осталось лишь 42. Причём пескарей осталось вдвое меньше, чем окуньков, а плотвы – вдвое больше, чем окуньков. Рыбки также заметили, что лишились одной плотвы, тогда как окуньков погибло в 8 раз больше, чем плотвы. Помоги рыбкам разобраться, сколько у них погибло и сколько осталось плотвы, пескарей и окуньков?
Просклоняй числительное 42.
Составь цепь питания из организмов, которые «обитают» в математической задаче.
(Математика – 3 балла, экология – по 1 баллу за каждое правильное звено в цепи, русский язык – по 1 баллу за правильную форму числительного в косвенном падеже.)
3. Школьник Паша собрал в коробку пауков и жуков – всего восемь штук. Если пересчитать, сколько всего ног в коробке, то окажется 54 ноги. Сколько в коробке жуков и сколько пауков?
Чем пауки отличаются от жуков?
Чем является слово ученик по отношению к слову школьник? Разбери по составу слово ученик.
(Математика – 2 балла, экология – 1 балл за каждый правильный признак, русский язык – по 1 баллу за правильный ответ.)
4. Нильс летел в стае на спине гуся Мартина. Он обратил внимание, что построение стаи напоминает треугольник: впереди вожак, затем – два гуся, в третьем ряду – три гуся и т.д.
Стая остановилась на ночлег на льдине. Нильс увидел, что расположение гусей на этот раз напоминает квадрат, состоящий из рядов, в каждом из которых располагается одинаковое количество гусей, причём число гусей в каждом ряду равно числу рядов.
Гусей в стае меньше 50. Сколько именно гусей в стае? Почему стая гусей летит клином, а во время ночлега принимает форму квадрата или круга?
Из перечня слов исключи лишнее и объясни свой выбор: летел, льдина, ночлег, Нильс, увидел, Мартин, количество.
(Математика – 3 балла, экология – 1 балл, русский язык – 2 балла.)
ЛИТЕРАТУРА
Белицкая Н.Г., Орг А.О. Школьные олимпиады // Начальная школа. – М.: Айрис-пресс, 2005.
- Большой справочник // Начальная школа. – М.: АСТ, Астрель, 2000.
- Воронина О.В. Сценарии внеклассных мероприятий // Начальное образование, 2007, № 1.
- Valeriu Guţu, Jgor Musteaţă, Galina Râbacova. Matematicile cangurului – 97. –
Сhişinǎu,1997.
Дробышев Ю.А. Олимпиады по математике: 1 – 4 классы: – М.: «Первое сентября», 2003.
- Ивакина Г.Н. Задания для проведения олимпиад по русскому языку // Начальная школа. – № 5. – 2006.
- Клепинина З.А. Тесты в системе повторения учебного материала при изучении окружающего мира // Начальная школа, 2004, № 1.
- Керова Г.В. Нестандартные задачи по математике: 1 – 4 классы: – М.: ВАКО, 2006.
- Мошнина Р.Ш. Окружающий мир. Материалы для проведения контрольных и проверочных работ 1 – 4 кл. – М.: АСТ – АСТРЕЛЬ, 2001.
- НаговскаяФ.Ш., Пивоварова Н.И., Талапова Т.А. Организация и проведение интегрированной олимпиады среди учащихся 4-х классов // Начальная школа плюс: до и после, 2006, № 12.
- Николау Л.Л. Задачи по математике повышенной трудности для начальных классов: Учебно-методическое пособие. – Бендеры: Полиграфист, 2000.
12. Николау Л.Л. Использование схематического моделирования при решении задач: Учебно-методическое пособие. – Тирасполь: Литера, 2006.
- Николау Л.Л. Учимся решать задачи на движение (3 – 5 классы): Учебно-методическое пособие. – Тирасполь, 2004.
- Олехник С.Н.., Нестеренко Ю.В., Потапов М.С. Старинные занимательные задачи. – М.: Наука, 1985.
- Пупышева О.Н. Олимпиадные задания по математике, русскому языку и курсу «Окружающий мир»: 1 - 4 классы. – М.: ВАКО, 2006.
- Русанов В.Н. Математические олимпиады младших школьников: Книга для учителя: – М.: Просвещение, 1990.
- Тарабарина Т.И., Соколова Е.И. И учеба, и игра: русский язык. – Ярославль: Академия развития, 1998.
18. Я иду на урок в начальную школу: Внеклассная работа. Олимпиады и интеллектуальные игры. – М.: Первое сентября, 2000.
