Рецензенты: И. Б. Левицкая проректор по научной работе гоу «Государственный институт развития образования», к п. н., доцент
| Вид материала | Книга |
- Н. А. Добролюбова, проректор по научной работе, 50.95kb.
- Учебно-методическое пособие удк 796/799 (075. 8) Печатается по решению ббк 74. 267., 3134.91kb.
- «Использование потенциала семьи в системе коррекционного воздействия на ребёнка», 138.16kb.
- Русские в Турции. 1920-1921, 352.95kb.
- Содержание подготовки методистов-организаторов в системе повышения квалификации работников, 284.53kb.
- Ильина Нина Федоровна,, 93.42kb.
- А. А. Левицкая, кандидат педагогических наук, доцент, 158.25kb.
- Тезисы выступления, 2699.95kb.
- Программа Челябинск 2011 г. Министерство образования науки Российской Федерации Южно-Уральский, 580.08kb.
- С. Х. Мухаметгалиева Елабуга, Елабужский государственный педагогический университет, 3598.14kb.
250. Борис, Андрей, Миша и Слава гуляли по парку с родителями и попросили их купить каждому по стакану сока. Все ребята разного возраста (8, 9, 10, 11 лет) и любят разные соки – грушевый, яблочный, вишневый и томатный. Определите их возраст и вкус, исходя из следующего:
Борису 8 лет и любит яблочный сок, Андрею – 10 лет – вишневый сок, Славе – 11 лет – томатный сок, Мише – 9 лет – грушевый сок. 251. Бригада трактористов вспахала в первый день третью часть площади одного участка, во второй день – четверть остатка, а в третий день вспахала оставшиеся 21 га. Определите общую площадь участка. 42 га. 252. Петя купил себе книгу, потратив на нее четверть из денег, которые имел, а на четверть из остатка он купил конфеты. Сколько денег было у него, если осталось 9 рублей? 16 рублей. 253. Всем знакома известная сказка «Репка», где дед, бабушка, внучка, собачка Жучка, кошка и мышка тянули репку и вытянули. Известно, что дед в 2 раза сильнее бабки, а бабка в 2 раза сильнее внучки, внучка в 2 раза сильнее Жучки, Жучка в 2 раза сильнее кошки, кошка в 2 раза сильнее мышки. Сколько мышек потребуется, чтобы вытянуть репку (если заменить остальных мышками)? 63 мышки. 254. В кассе Одесского театра продавались билеты на спектакль. 1/5 часть билетов была продана по 10 гривен за билет, половина из остатка по 20 гривен, а остальные билеты в количестве 1200 штук по 30 гривен каждый. Сколько денег собрал кассир после продажи билетов? 66 000 гривен. 255. Половина одного числа, увеличенная на 8 была умножена на 6. Полученное произведение уменьшено на 18, а результат разделен на 6 и получили 10. Найдите число? При нахождении числа, воспользуемся методом решения с конца ((8 · 6 + 18) : 6 – 8)·2 = 6. 256. Найдите значение x, используя метод решения с конца: 1) 12000 -(2x+50):1000+2800=10000; 2) ((5x+178) ·15+90):45=63; 3) ((x:7+108):4.10 -192):4=87; 4) 2520 : (480-3000:x)+48)·8=576; 5) (((134·x -3179)+856).81):333=315; 6) ((8600-325· (576:x))·42):165 - 220=480. 1) 275; 2) 1; 3)756; 4) 8; 5) 27; 6) 32. 257.Трое мужчин пришли в парикмахерскую. Побрив первого, парикмахер сказал: «Посмотри, сколько денег в ящике стола, положи еще столько и возьми сдачи 2 рубля». То же самое сказал парикмахер и второму, и третьему. После того как трое ушли, оказалось, что в кассе нет денег. Сколько денег было в кассе перед тем, как заплатил первый мужчина? 1 руб. 75 коп. 258. Два дровосека Николай и Павел работали в лесу и сели обедать. У Николая было четыре ломтика хлеба, у Павла – семь. К ним подошел охотник и попросил: «Братцы, я заблудился в лесу, до деревни далеко, а я голоден. Поделитесь вашим хлебом». «Давай пообедаем вместе», – ответили лесорубы. 11 ломтиков хлеба были поровну разделены между тремя, для этого каждый ломтик был разделен на три части. Пообедав, охотник дал лесорубам 11 рублей за хлеб, которым его накормили. После ухода охотника Николай сказал: «По-моему, деньги нужно разделить поровну». Павел возразил: «За 11 ломтиков имеем 11 рублей. У тебя было 4 ломтика, тебе и полагается 4 рубля, а за мои 7 ломтиков мне полагается 7 рублей». Кто из них правильно рассуждал? Оба дровосека ошибались. Николай должен получить 1 руб., а Павел 10 руб. 259. Одного старика спросили, в скольких войнах он участвовал. Старик ответил: «В стольких войнах, сколько будет, если взять 1/27 от моих лет или 1/8 от возраста моего внука, или столько, сколько лет его сыну. А мой возраст ближе к 80, чем к 90». В скольких войнах участвовал старик? В трех войнах. 260. Мальчик и овчарка весят столько, сколько 5 ящиков. Овчарка весит столько, сколько четыре кошки. 2 кошки и овчарка весят сколько, сколько 3 ящика. Сколько кошек уравновесят мальчика? 6 кошек. 261. Гусеница бабочки – капустницы съедает за день до 10 г капусты. Синица съедает ежедневно до 100 гусениц. Посчитайте, сколько капусты «экономит» за один месяц «работы» (30 дней) семья синиц, состоящая из самца, самки и пяти птенцов, если считать, что птенец съедает в два раза меньше взрослой синицы? 135 кг. 262. Петя купил 2 ручки и 4 карандаша и заплатил 8 рублей. Зная, что одна ручка в 2 раза дороже карандаша, определите стоимость ручки. 2руб. 263. Для школы купили 3 больших мяча и 2 маленьких на сумму 33 гривны. Найти сколько стоит один мяч каждого вида, если большие мячи в 3 раза дороже, чем маленькие. 3 гривны; 9 гривен. 264. Окопали 4 ряда черной смородины и 10 рядов красной смородины. Всего окопали 120 кустов смородины. Сколько кустов красной смородины в одном ряду, если их в 2 раза больше, чем черной? 10 кустов. 265. 57 л молока разлили в 4 бидона и 3 банки. Сколько литров молока в 1 бидоне и в 1 банке, если емкость банки в 4 раза меньше, чем бидона? 12 л; 3 л. 266. На 6 кофт и на 4 пальто пришито 64 пуговицы. Сколько пуговиц пришили на одно пальто и на одну кофту, если на 1 кофту понадобилось в 2 раза больше пуговиц, чем на одно пальто? 4 пуговицы; 8 пуговиц. 267. Найти числа a, b, c, d, зная, что: а) a = b · 3; c = b + 10; d = a + 6; a + b + c + d = 80; б) b + c = 399; c – d = 325; d · 2 = 108; a + b + c + d = 1000. а) а = 24; b = 8; с = 18; d = 30; б) а = 547; b = 20; с = 379; d = 54. 268. 594 литра вина было разлито в сосуды емкостью по 1 л, 5 л и 50 л. Число сосудов емкостью 1 л в 6 раз больше, чем число сосудов емкостью 50 л, а число сосудов емкостью 5 л в 3 раза меньше, чем число сосудов емкостью 1 л. Сколько сосудов каждой емкости было использовано? 54 сосуда ёмкостью 1 л; 18 сосудов ёмкостью 5 л; 9 сосудов емкостью 50 л. 269. (Старинная). 5 волов и 3 барана стоят 13 золотых монет, а 2 вола и 8 баранов стоят 12 золотых монет. Сколько стоит 1 вол и 1 баран? Решение: Решим эту задачу методом уравнивания данных (или методом сравнения). Для этого запишем условие задачи в следующем виде: 5в; 3б; 13 золотых монет. 2в; 8б; 12 золотых монет. Нужно приравнять количество волов и баранов. Сравним количество волов, для этого 1 строку данных умножим на 2, а вторую на 5. Получим: 10в; 6б; 26 золотых монет. 10в; 40б; 60 золотых монет. Отсюда, 40 – 6 = 34 (барана) будут стоить 60 – 26 = 34 (золотые монеты), а один баран стоить: 34 : 34 = 1 (золотую монету). Подставляя этот результат в первую строку данных, получим, что 3 барана стоят 3 золотые монеты, а 5 волов будут стоить 13 – 3 = 10 (золотых монет). Откуда 1 вол стоит 10 : 5 = 2 (золотые монеты) 270. На товарную станцию прибыли вагоны с зерном и овощами. 4 вагона с зерном и 3 вагона с овощами имеют груз массой 2568 ц, а 2 вагона с зерном и 2 вагона с овощами имеют груз массой 1382 ц. Сколько центнеров зерна было в одном вагоне? 495 ц зерна. 271. На одном складе было 10 мешков гороха и 6 мешков фасоли общим весом 900 кг. А на другом складе было 4 мешка фасоли и 5 мешков гороха общим весом 500 кг. Сколько весит мешок фасоли и мешок гороха в отдельности? 1 мешок гороха – 60 кг; 1 мешок фасоли – 50 кг. 272. На 4 детских платья и на 3 платья для взрослых израсходовали 13 м ткани, а на 3 детских и 5 взрослых платьев израсходовали 18 м ткани. Сколько метров ткани нужно для одного детского платья? А для взрослого? 1 м; 3 м. 273. Для 4-х коз и 2-х телят было израсходовано 40 кг сена. А если было бы 3 козы и 4 теленка, то они бы съедали 50 кг сена. Сколько кг сена съедает за один день 1 коза и 1 теленок в отдельности? Коза – 6 кг; телёнок – 8 кг. 274. 6 мотоциклов и 4 легковых автомобиля израсходовали 62 л бензина на 100 км, а 7 мотоциклов и 8 легковых автомобилей израсходовали 99 л бензина на 100 км. Сколько литров бензина израсходовал один мотоцикл на 100 км? А легковой автомобиль? Мотоцикл – 5 л, лёгковой автомобиль – 8 л. 275. Для пошивки … простыней и … наволочек израсходовано … метров бельевого материала, а для пошива … простыней и … наволочек израсходовано … … метров бельевого материала. Определите расход материала на одну простыню и на одну наволочку. (Подберите данные и решите задачу). 276. В магазине для продажи картофель разложили в пакеты по 3 кг и 5 кг, всего 24 пакета. Масса всех пакетов по 5 кг равна массе всех пакетов по 3 кг. Сколько пакетов по 3 кг? Предположим, что 3 пакета по 5 кг и 5 пакетов по 3 кг. Тогда 5 · 3 = 3 · 5, а пакетов будет 3 + 5 = 8. Но пакетов 24, что в 3 раза больше чем 8. Значит в 3 раза нужно увеличить предполагаемые числа: 5 · 3 = 15 (пакетов) по 3 кг. 277. Для туристической поездки на теплоходе по Черному морю было продано 124 билета I и II класса на сумму 4944 гривны. Один билет I класса стоит 56 гривен, а один билет II класса – 36 гривен. Сколько билетов каждого класса было продано? Предположим, что все 124 билета были 1 класса, тогда 56 · 124 = 6 944 (гривны) заплатили за них. Это на 2000 гривен больше (6 944 – 4 944 = 2 000), чем настоящая выручка. Билет I класса дороже, чем билет II класса на 20 гривен. 2 000 : 20 = 100 (билетов) – II класса были проданы. 124 – 100 = 24 (билета) – I класса были проданы. 278. Велосипедист поднимается на горку со скоростью 6 км/час, а возвращается со скоростью 20 км/час. Зная, что на дорогу туда и обратно он потратил 3 ч 15 мин., найти длину пути. 15 км. Эту задачу можно решить также методом предположения. 279. Товарный состав из паровоза с тендером и 50 груженых вагонов имеет общий вес 1472 т, причем паровоз с тендером весит 84 т. Груженые вагоны были весом по 22 т и по 34 т. Сколько было в составе вагонов по 22 т и по 34т? 24 вагона по 34 т и 26 вагонов по 22 т. 280. На платформу погрузили по 70 сосновых и еловых бревен, общим весом 165 ц. Сосновое бревно весило 210 кг, а еловое – на 40 кг больше, чем сосновое. Сколько было тех и других бревен? 45 брёвен еловых и 25 брёвен сосновых. 281. Из … м шерстяной материи сшито … мужских и женских костюмов. На один мужской костюм израсходовано … м материи, а на женский … м. Сколько сшито женских костюмов? (Подобрать данные и решить задачу). 282. Магазин получил а пакетов пшеничной и гречневой крупы общим весом b кг. Гречневая крупа расфасована по 2 кг в каждый пакет, а пшеничная – по 3 кг в каждый пакет. Сколько пакетов тех и других получил магазин? (в - 2а) – пакетов пшеничной крупы; (3а – в) – пакетов гречневой крупы. 283. Чтобы открылись ворота Руслан должен был набрать шифр к замку, состоящий из десятизначных чисел чисел, в записи каждого из которых крайняя левая цифра обозначает количество единиц в этом числе; вторая – количество двоек, третья – количество троек, а последняя цифра 5 – количество нулей. Помогите Руслану набрать шифр. Запишем последние цифры в таком виде: 000 005. К этому числу слева надо приписать цифры, среди которых имеются цифры 1, 2, 3. Двоек и троек должно быть по одной, тогда единиц две. В результате имеем одно число 2 113 000 005. Все остальные числа получим, меняя местами 3 и 0. Имеем: 2 110 300 005; 2 110 030 005; 2 110 003 005; 2 110 000 035 – требуемый шифр. 284. В битве с трехглавым и треххвостым змеем Иван-царевич одним ударом меча может срубить либо одну голову, либо две головы, либо один хвост, либо два хвоста. Если срубить одну голову – новая вырастет, если срубить один хвост – два новых вырастут, если срубить два хвоста – голова вырастет, если срубить две головы – не вырастет ничего. Посоветуйте Ивану-царевичу, как быть, чтобы он смог срубить змею все головы и хвосты. Срубить одну голову нельзя – новая вырастает. Надо добиться такого положения, чтобы голов осталось чётное количество, хвостов – ни одного. Но для этого сначала надо добиться, чтобы хвостов было чётное количество. Получаем такое решение: 1 удар: срубить 2 хвоста – станет 4 головы и 1 хвост; 2 удар: срубить 1 хвост – станет 4 головы и 2 хвоста; 3 удар: срубить 1 хвост – станет 4 головы и 3 хвоста; 4 удар срубить 1 хвост – станет 4 головы и 1 хвост; 5 удар: срубить 2 хвоста – станет 5 голов и 2 хвоста; 6 удар: срубить 2 хвоста – станет 6 голов; 7, 8, 9 удары; срубить по 2 головы. 285. Периметр листа картона, имеющего форму квадрата, равен 28 дм. Сколько квадратных сантиметров содержит его площадь? 1) 28 : 4 = 7 (дм) – длина стороны квадрата;
Площадь квадрата равна 4 900 см2. 286. Из металлической заготовки вытачивают деталь. Стружки, которые получились при вытачивании 8 деталей, можно переплавить в одну заготовку. Сколько можно сделать деталей из 64 заготовок? 1) 64 : 8 = 8 (заготовок) – можно изготовить из отходов при вытачивании 64 деталей; 2) 8 : 8 = 1 (деталь) – может быть изготовлена из отходов при вытачивании 8 деталей; 3) 64 + 8 + 1 = 73 (детали) Из 64 заготовок можно изготовить 73 детали. 287. Сколько всего ударов в сутки делают часы, если они бьют каждые полчаса по одному разу, а каждый час соответственно 1, 2, 3, … 12 раз? 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12) х 2 + 24 = 180 (ударов.) 288. Периметр квадрата равен 20 см. На сколько квадратных сантиметров увеличится площадь квадрата, если его периметр увеличить на 12 см? Так как у квадрата все стороны равны, то: 1) 20 : 4 = 5 (см) – длина одной стороны; 2) 5 х 5 = 25 (см2) – площадь квадрата; 3) 12 : 4 = 3 (см) – на столько увеличилась сторона;
Можно решить эту задачу иначе, 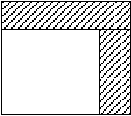 3 см 3 см5 см 5 см 3 см Для того чтобы ответить на вопрос задачи, следует найти сумму площадей заштрихованных прямоугольников. 1) 20 : 4 = 5 (см) – длина стороны квадрата; 2) 5 + 3 = 8 (см) – длина верхнего прямоугольника; 3) 8 х 3 = 24 (см2) – площадь верхнего прямоугольника; 4) 5 х 3 = 15 (см2) – площадь правого прямоугольника; 5) 24 + 15 = 39 (см2) – увеличилась площадь квадрата. 289. Нарисуйте прямоугольник, площадь которого 12 см2, а сумма длин сторон 26 см. Так как площадь прямоугольника равна произведению длины на ширину, то нам нужно представить число 12 в виде произведения двух множителей. Это можно сделать следующим образом: 12 = 1 х 12 12 = 2 х 6 12 = 3 х 4 Стороны прямоугольника могут быть равны: а = 1 а = 2 а = 3 b = 12 b = 6 b = 4 Выберем из них те, которые удовлетворяют второму условию. Для этого вычислим сумму их длин: 1 х 2 + 12 х 2 = 2 + 24 = 26 – удовлетворяет условию; 2 х 2 + 6 х 2 = 4 + 12 = 16 – не удовлетворяет; 3 х 2 + 4 х 2 = 14 – не удовлетворяет.  1 см 1 см12 см 290. Сколько понадобится времени, чтобы записать подряд все числа от 5 до 105, если на запись каждой цифры расходуется секунда? Ответ вырази в минутах. Узнаём сначала, сколько однозначных, двузначных и трёхзначных чисел находится в промежутке от 5 до 105. Однозначных: 5 (от 5 до 9). Двузначных: 90 (от 10 до 99). Трёхзначных: 6 (от 100 до 105). Теперь узнаём, сколько времени понадобится для записи всех чисел от 5 до 105. 1 х 5 + 2 х 90 + 3 х 6 = 5 + 180 + 18 = 203 (с). 203 с = 3 мин 23 сек. 291. Однажды в вагоне Таня стала зашифровывать слова, заменяя буквы их номерами в алфавите. Когда она зашифровала пункты прибытия и отправления поезда, то с удивлением обнаружила, что они записываются с помощью лишь двух цифр: 211221 – 21221. Откуда и куда идёт поезд? Выпишем все буквы алфавита.  А Б В Г Д Е Ё Ж З И Й К Л М Н О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Первое слово может начинаться либо на вторую, либо на двадцать первую букву алфавита: Б или У. Вторая буква тогда может быть либо 1 или 11, либо 1 или 12 (А или Й, А или К). БА или БЙ, УА или УК. Рассмотрим сначала первый вариант: БА. Третьей буквой может быть либо А (1), либо К (12), то есть имеем буквосочетания БАА или БАК. Тогда четвёртая буква для буквосочетания БАА будет либо Б (2), либо Ф (22), то есть получаем БААБ или БААФ. Заканчивая анализ этого варианта, имеем БААБУ, БААФА, БААББА. Очевидно, что полученные буквосочетания не являются названиями городов. Четвёртой буквой буквосочетания БАК может быть либо У (21), либо Б (2). В первом случае имеем слово БАКУ, во втором – название города не получилось. Таким образом, город из которого идёт поезд, это БАКУ. Второе слово может начинаться либо с буквы Б (2), либо с буквы У (21). Тогда за буквой Б может следовать либо А (1), либо К (12). В этом случае имеем буквосочетание БА или БК. За буквой У может следовать либо буква Ф (22), либо Б (2). Тогда имеем буквосочетания УФ и УБ. Очевидно, что присоединяя к буквосочетанию УФ последнюю букву А (1), получаем город УФА. Таким образом, поезд следовал по маршруту БАКУ - УФА. 292. Вставьте пропущенное слово. х – 1 = 1 февраль 18 – 2х = 10 апрель 48 = 5х + 3 ? Решим первое уравнение. х – 1 = 1 х = 2 Справа написан месяц февраль. Он является вторым месяцем в году. Проверим подмеченную закономерность на следующем примере. Для этого решим второе уравнение. 18 – 2х = 10 2х = 18 – 10 2х = 8 х = 4 Апрель является четвёртым месяцем в году. Значит, найденная закономерность правильная. Решаем третье уравнение. 48 = 5х + 3 5х = 48 – 3 5х = 45 х = 9 Следовательно, справа должен стоять девятый месяц. Им является сентябрь. 293. Определите неизвестное число. 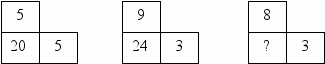 Ответ: 21 = 8 · 3 – 3 либо 22 = (8 + 3) · 2
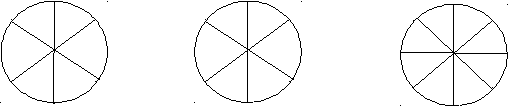 а) б) в) а) б) в)? 10 ? 8 ? 4 0 6 39 13 4 9 3 16 1 3 24 18 2 25 Ответ: а) 15; б) 6 или 54; в) 5 или 625. 295. Запишите пропущенное число. 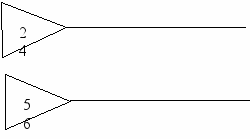 1; 2; 3; 4; 6; 8; 12; 24. 1; 2; ?; 7; ?; 14; ?; 56. Ответ: 4; 8. 296. Запишите пропущенное число. 5 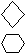 х – 3 17 х – 3 17х – 5 ? Ответ: 1.
МАТЕМАТИКА 3 ≤ Х ≤ 6 ТЕМА ДЕЦИМЕТР 5 ≤ Х ≤ 8 … Ответ: МЕТР.
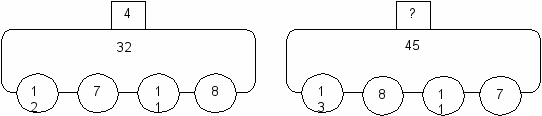 Ответ: 5. 299. Вместо вопросительного знака найдите число или рисунок. 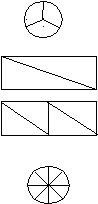 а) 25 · 3 – 9 · 6 7 б) 8 + 17 · 4 – 68 4 в) 3 · 15 – 3 · 3 ? г) ? + 13 5 д) 27 + 30 : 15 – 11 ? 6 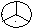 Ответ: в) 9; г) 27; д) |
