Рецензенты: И. Б. Левицкая проректор по научной работе гоу «Государственный институт развития образования», к п. н., доцент
| Вид материала | Книга |
- Н. А. Добролюбова, проректор по научной работе, 50.95kb.
- Учебно-методическое пособие удк 796/799 (075. 8) Печатается по решению ббк 74. 267., 3134.91kb.
- «Использование потенциала семьи в системе коррекционного воздействия на ребёнка», 138.16kb.
- Русские в Турции. 1920-1921, 352.95kb.
- Содержание подготовки методистов-организаторов в системе повышения квалификации работников, 284.53kb.
- Ильина Нина Федоровна,, 93.42kb.
- А. А. Левицкая, кандидат педагогических наук, доцент, 158.25kb.
- Тезисы выступления, 2699.95kb.
- Программа Челябинск 2011 г. Министерство образования науки Российской Федерации Южно-Уральский, 580.08kb.
- С. Х. Мухаметгалиева Елабуга, Елабужский государственный педагогический университет, 3598.14kb.
200. В соревнованиях по гимнастике Заяц, Мартышка, Удав и Попугай заняли первые 4 места. Определите, кто какое место занял, если известно, что Заяц – 2, Попугай не стал победителем, но в призеры попал, а Удав уступил Мартышке. Занесем условие задачи в таблицу 2, и, где возможно, расставим плюсы и минусы: Таблица 2
Получилось, что Мартышка и Удав на первом и четвертом месте, но так как по условию Удав уступил Мартышке, то получается, что на первом месте – Мартышка, на втором – Заяц, на третьем – Попугай и на четвертом – Удав. 201. На новогоднем утреннике три подруги, Аня, Вера и Даша, были активными участниками, одна из них была Снегурочкой. Когда их подруги спросили, кто же из них был Снегурочкой, то Аня им сказала: «На ваш вопрос каждая из нас даст свой ответ. По этим ответам вы должны догадаться сами, кто из нас в действительности был Снегурочкой. Но знайте, что Даша всегда говорит правду». – «Хорошо, – ответили подруги, - послушаем ваши ответы. Это даже интересно». Аня: «Снегурочкой была я». Вера: «Я не была Снегурочкой». Даша: «Одна из них говорит правду, а другая неправду». Так кто же из подруг на новогоднем утреннике была снегурочкой? Из утверждения Даши получаем, что среди высказываний Ани и Веры одно истинное, а другое – ложное. Если ложным будет высказывание Веры, то получим, что и Аня, и Вера были Снегурочками, чего быть не может. Значит, ложным должно быть высказывание Ани. В этом случае получаем, что Аня Снегурочкой не была, не была Снегурочкой и Вера. Остается, что Снегурочкой была Даша. 202. Три ученицы, Алла, Вера и Даша, на новогодний бал пришли одна в красном платье, другая в белом, третья в синем платье. Среди высказываний: Алла была в красном; Вера не в красном; Даша не в синем плате; – одно верно, а два других неверны. В каком платье была каждая из учениц? Рассмотрим три случая, когда верным было первое высказывание, второе и третье (таб.3). Таблица 3
Вера – в красном, Даша – в белом, Алла – в синем. 203. Вике на день рождения подарили книгу Дж. Родари «Приключения Чипполино», а Симе – «Приключения Буратино». Прочитав эти книги, девочки дали их своим друзьям. Вика дала книгу Поле, Катя взяла у Симы, Оля читала книгу «Приключения Чипполино» после Димы, а Дима брал ее у Поли. Миша читал книгу после Кати, и, прочитав, отдал ее Гале. После Гали книгу читала Аня и отдала ее Яне. Сколько человек прочитали книгу «Приключения Чипполино» и сколько – «Приключения Буратино»?  Рассмотрим отношение «прочитать книгу раньше». Поскольку по условию задачи дети читали две книги – «Приключения Чипполино» и «Приключения Буратино», то мы получим сразу два графа. Все условия задачи представим графически, после чего один из графов для наглядности выделим другим цветом. Поскольку Симе подарили «Приключения Буратино», то, судя по графу (пунктирной линии), эту же книгу прочитали еще 5 человек, а «Приключения Буратино» вместе с Викой прочитали еще 3 человека. К С М О В П Я Д Г А 204. На карточке нарисованы отрезок, круг, треугольник, звезда и квадрат. В каком порядке они нарисованы, если известно, что: отрезок не рядом с треугольником; треугольник не рядом с кругом; круг не рядом со звездой, а звезда не рядом с отрезком; треугольник не рядом с квадратом, а квадрат не рядом с кругом; звезда располагается рядом с квадратом и находится справа от него? Начнем с условия, что звезда располагается рядом с квадратом и находится справа от него. По условию рядом с квадратом не треугольник и не круг, остается, что рядом с квадратом (слева от него) находится отрезок. Рядом с отрезком – не треугольник; остается, что слева от отрезка находится круг, а справа от звезды – треугольник. В итоге получили, что геометрические фигуры расположены в следующем порядке: круг, отрезок, квадрат, звезда, треугольник. 205. Есть краски зеленого, красного, синего, желтого, оранжевого цветов. Сколькими способами можно раскрасить трехэтажные домики в три цвета, при условии, что цвета не должны повторяться? Проведем рассуждения для домика, верхний этаж которого покрасили зеленой краской. Итак, если верхний этаж зеленый, то второй этаж можно покрасить в любой из оставшихся четырех цветов, т.е. от верхней точки проводим четыре отрезка. Если верхний этаж зеленый, а второй, например, красный, то третий этаж может быть одним из оставшихся трех цветов, т.е. от точки «к» второго этажа вниз проводим три отрезка. Таким образом, если верхний этаж дома покрашен в зеленый цвет, то имеющимися красками его этажи можно покрасить 12 способами. Если же верхний этаж дома покрасили, например, красным цветом, то все дальнейшие рассуждения будут такими же, как и в предыдущем случае, т.е. дом так же можно будет покрасить 12 способами. Поэтому можно ограничиться построением графа только для случая покраски верхнего этажа дома каким-либо одним цветом. Если при покраске верхнего этажа определенным цветом получается 12 вариантов, а верхний этаж, в свою очередь, можно покрасить 5 способами, то всего имеющимися красками дом можно раскрасить 60 способами. 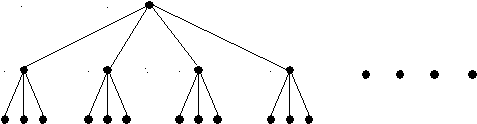 зк с ж о к ж с о ж с о к с о к ж о к ж с 206. На одной планете люди ходят только парами, причем один человек всегда говорит только правду, а другой всегда лжет. Случайно залетевший на эту планету путешественник спросил одного человека из пары: «Куда я попал?» – «Вы на планете, где все говорят правду», – был ответ. Тогда путешественник спросил его спутника: «Как тебя зовут?». – «Джон», – ответил тот. Правда ли это? Да, это правда, так как первый человек сказал неправду. Это значит, что второй человек из пары должен сказать правду. 207. Принесли 5 чемоданов и 5 ключей от этих чемоданов, но неизвестно, какой ключ от какого чемодана. Сколько проб придется сделать в самом худшем случае, чтобы подобрать к каждому чемодану свой ключ? Чтобы подобрать первый ключ к чемодану, требуется 4 пробы, второй ключ – 3 пробы, третий ключ – 2 пробы и четвертый ключ – 1 проба. Всего потребуется 4 + 3 + 2 + 1 = 10 проб. 208. В коробке лежат одинаковые по форме конфеты двух сортов: 10 конфет с мармеладной начинкой и 6 конфет с шоколадной. Карлсон съел 8 конфет. Была ли среди них конфета с шоколадной начинкой? Какое наименьшее число конфет надо съесть, чтобы среди них была хоть одна конфета с шоколадной начинкой? Ответ: Конфеты с шоколадной начинкой среди съеденных могло и не быть, так как Карлсон мог съесть все 8 конфет с мармеладной начинкой. Надо съесть 11 конфет, чтобы среди них была обязательно хотя бы одна конфета с шоколадной начинкой. 209. В классе 30 человек. В диктанте Витя Малеев сделал 12 ошибок, а каждый из остальных – не больше. Докажите, что, по крайней мере, трое учеников сделали одинаковое количество (быть может, и ноль) ошибок. Решение: Разделим учеников на группы следующим образом: в одну группу войдут ученики, сделавшие одинаковое число ошибок. Таких групп будет 13. Если бы в каждой группе было только по 2 ученика, то всего было бы 26 учеников, а у нас их 30. Тогда 27-й ученик сделает столько же ошибок, как и два других их любой группы. 210. В ящике лежали цветные карандаши: 10 красных, 8 синих и 4 желтых. В темноте берем из ящика карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них заведомо было: а) не менее 4-х карандашей одного цвета; б) не менее 6-ти карандашей одного цвета; в) хотя бы 1 карандаш каждого цвета; г) не менее 6-ти синих карандашей? а) 10 карандашей; б) 15 карандашей; в) 19 карандашей; г) 20 карандашей. 211. У одного путешественника не было денег, но была золотая цепочка из семи звеньев. Хозяин гостиницы, к которому обратился путешественник с просьбой о ночлеге, согласился держать постояльца неделю, если тот будет отдавать ему ежедневно в виде платы одно из звеньев цепочки. Какое одно звено надо распилить, чтобы путешественник мог ежедневно в течение семи дней расплачиваться с хозяином гостиницы? (При расчете хозяин может возвращать постояльцу полученные у него раньше звенья.) Надо распилить третье звено, тогда получится одно звено и два обрывка длиной 2 звена и 4 звена. В первый день путешественник может расплачиваться одним звеном; во второй день хозяин возвращает постояльцу это звено, а путешественник отдает ему 2 звена; за третий день 2 + 1 звено, за четвертый день 3 звена возвращаются, и постоялец отдает 4 звена и т.д. 212. В семье трое детей: два мальчика и девочка. Их имена начинаются с букв А, В, Г. Среди А и В есть начальная буква имени одного мальчика. Среди В и Г есть начальная буква имени одного мальчика. С какой буквы начинается имя девочки? Имя девочки начинается с буквы В. 213. Вдоль дороги расположено 5 домов. Расстояние между двумя соседними домами равно 10 км. Возле какого дома надо вырыть колодец, чтобы сумма расстояний от колодца до домов была как можно меньше? Чему равно это расстояние? Колодец выгоднее вырыть возле среднего дома. Проверим это, сделав необходимые вычисления. Если вырыть колодец около крайнего дома, то сумма всех расстояний до остальных домов равна 10 + 20 + 30 + 40 = 100 (м). Если вырыть колодец возле второго с краю дома, то сумма всех расстояний до остальных домов равна 10 + 10 + 20 + 30 = 70 (м). Если вырыть колодец возле среднего дома, то сумма всех расстояний до остальных домов равна 10 + 20 + 10 + 20 = 60 (м) – наименьшая сумма расстояний. 214. С хозяйством попа справляются 10 работников. Каждый работник в день съедает каравай хлеба и другие продукты. Поп принял на работу Балду. Живет Балда в поповом доме, Спит себе на соломе, ест за четверых, Работает за семерых. Поп прогнал лишних работников. Сколько караваев хлеба экономил поп ежедневно? 3 каравая. 215. Поросята Ниф-Ниф и Нуф-Нуф бежали от волка к домику Наф-Нафа. Волку бежать до поросят (если бы они стояли на месте) 4 мин. Поросятам бежать до домика Наф-Нафа 6мин. Волк бежит в два раза быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа? Успеют. 216. Сколько всего можно составить 4-х значных чисел, сумма цифр которых равна 3? Перечислите эти числа. 3000, 2100,2001, 2010, 1200, 1002, 1020, 1110, 1011, 1101. 217. Полтрети числа – число 100. Найдите это число. 600. 218. Расшифруйте запись, если известно, что оба слагаемых и сумма не изменяется, если прочитать их справа налево. аа + всв = кллк Ответ: 22 + 979 = 1001. 219. Собака усмотрела зайца в 150 саженях от себя. Заяц пробегает за 2 мин 500 саженей, а собака за 5 мин 1300 саженей. За какое время собака догонит зайца? За 15 мин. 220. Бидон с молоком весит 18 кг, а бидон без молока – 2 кг. Сколько весит бидон, заполненный молоком на четверть? 6 кг. 221. Журавли обычно летают так, что образуют треугольник: впереди один журавль (вожак). За ним два, потом три журавля и т.д. Сколько летело журавлей, если в последнем ряду их было 15? 15 + 14 + 13 + 12+11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 120. 222. Как поставить скобки, чтобы получить верное равенство: 9664 : 32 – 2 . 195 – 37 . 5 = 3000? (9664 : 32 – 2) · (195 – 37 · 5) = 3000. 223. Для окраски кубика с ребром 2 см требуется 1 г краски. Сколько краски потребуется для окраски кубика с ребром 6 см? На одной грани большого кубика можно уложить 9 граней меньшего кубика, поэтому для окраски одной грани большого кубика краски надо в 9 раз больше, чем для окраски меньшего кубика, а следовательно, для окраски всего большого куба надо краски в 9 раз больше, т.е. 9 грамм. 224. При делении некоторого числа на 180 в остатке получилось 120. Разделится ли данное число на 60? Да. 225. Как изменится четырехзначное число, написанное различными цифрами, среди которых нет нуля, если поменять местами его цифры в разряде тысяч и разряде сотен? Если число сотен больше числа тысяч, тогда увеличится. Если же число сотен меньше числа тысяч, тогда уменьшится. 226. К двузначному числу прибавили 3, оказалось, что сумма делится на 3. К этому же двузначному числу прибавили 7, полученная сумма разделилась на 7. Когда от него отняли 4, то оказалось, что полученная разность делится на 4. Найдите это двузначное число. 3 · 4 · 7 = 84. 227. В ящике 10 пар черных перчаток и 10 пар красных. Сколько перчаток необходимо вынуть из ящика наугад, чтобы наверняка среди них были две перчатки одного цвета? (Две черных, безразлично на какую руку). 22 перчатки. 228. Белая мышка бежала от сарая к дому, а серая – от дома к сараю. Они выбежали (одна из дома, другая из сарая) одновременно. Через 5 мин белая мышка была ближе к дому, чем серая к сараю. Какая мышка бежала медленнее? Серая мышка. 229. Сколько всего 4-х значных чисел можно составить из цифр 0 и 1, если каждая цифра повторяется два раза? Перечислите эти числа. 1001; 1100; 1010. 230. В вершинах квадратной клумбы растут кусты – всего 4 куста. Площадь клумбы увеличили в 2 раза, не выкапывая кустов. Расширенная клумба тоже квадратная и внутри нее кустов нет. Как это сделали? Выполни рисунок. 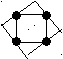 Ответ: 231. На какое однозначное число, не равное 0, надо умножить 142857, чтобы получилось число, записанное одинаковыми цифрами? 142 857 · 7 = 999 999. 232. Замените буквы в фигуре числами, если известно, что А – в 2 раза больше С, В – 1/4 от А + С, С – произведение 3 и 4, D – сумма А, В, С.
С = 12; А = 24; В = 9; Д = 45. 233. В трех ящиках 22, 14 и 12 яблок. Требуется путем трех перекладываний уравнять число яблок в этих ящиках, но из одного ящика можно перекладывать в другой ящик столько, сколько яблок имеется во втором ящике. Как это можно сделать? 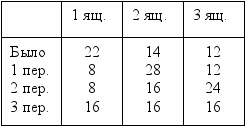 234. Нарисуйте прямоугольник с наибольшей площадью, периметр которого равен 12 см. Квадрат со стороной 3 см. 235. Как надо расположить 16 палочек длиной 1 дм таким образом, чтобы они образовали прямоугольник наименьшей площади? Чему равна эта площадь? 7 · 1 = 7 (кв. дм.) 236. Начертите прямоугольники, периметры которых равны 12 см. Длины сторон могут быть выражены только целыми числами в см. Определите площадь начерченных прямоугольников. 2 · 4 = 8 см2; 1 · 5 = 5 см2. 237. Турист проходит 6 км за 1 час. Сколько метров он проходит за 1 мин? 100 м. 238. Квадратный лист бумаги со стороной 8 см разрезали следующим образом: через середины каждой пары соседних сторон провели карандашом отрезки и по ним выполнили разрезы. Какова площадь получившегося квадрата? 32 см2. 239. Нарисуйте прямоугольник, площадь которого 12 см2, а сумма длин сторон 26 см. Это прямоугольник со сторонами 1 см и 12 см.
0. 241. На какое однозначное число нужно умножить 123 456 789, чтобы в результате получилось новое число, записанное одними единицами? 123 456 789 · 9 = 111 111 111. 242. В каждом из четырех полков выбрано по 4 офицера разных званий (a, b, c, d). Требуется разместить этих шестнадцать офицеров в виде квадрата так, чтобы в каждом горизонтальном и вертикальном ряду был офицер каждого звания и представитель каждого полка. Как это сделать? Ответ: а 1 в2 с3 d4 с4 d3 а2 в1 в3 а4 d1 с2 d2 с1 в4 а3 243. Запишите шесть однозначных чисел при помощи четырех четверок, знаков действий и скобок. 4 · 4 + 4 : 4 = 1; 4 : 4 + 4 : 4 = 2; (4 · 4 – 4) : 4 = 3. 244. Маленький Мук и королевский скороход соревновались в беге по дорожке длиной – 30 км, которая шла вокруг леса. По условию соревнования выигрывает тот, кто обгонит другого, пробежав на круг больше. Скороход делает круг за 10 минут, а маленький Мук – за 6 минут. Оба бегут равномерно. Через сколько минут маленький Мук обгонит скорохода? 15 минут. 245. Школьная медсестра измерила рост Кати, Раи, Миши, Антона, Лизы и Гриши, но уронила свои записи и перепутала их. Помогите ей определить рост ребят, если известны числа, которые она написала (150, 152, 153, 155, 158, 159), и следующие факты:
2) Рая выше Миши на 2 см; 3) Лиза выше остальных девочек и Миши, но ниже, чем Гриша и Антон. Катя – 153 см; Рая – 152 см; Миша – 150 см; Антон – 158 см; Лиза – 155 см; Гриша – 159 см. 246. Дима, Боря и Света любят разные цвета – красный, синий и белый, но кто какой, неизвестно. Возраст ребят тоже неизвестен, мы знаем только, что кому-то из них 9 лет, кому-то 10 лет, а кому-то 11. Известно также следующее:
2) Самый молодой любит белый цвет. Определите возраст каждого ребенка, и кто из них какой цвет любит. Света (белый) – 9 лет; Дима (синий) – 10 лет; Боря (красный) – 11 лет. 247.Три мамы, которым 32, 38 и 41 год, варили варенье. Одна – из яблок, другая из слив, третья – из вишен. Их фамилии мы знаем: Белова, Краснова и Чернова. Определите возраст каждой, и что за варенье каждая из них варила, исходя и следующего: 1) Белова старше Красновой, но моложе той мамы, которая варила варенье из яблок; 2) Самая молодая из них приготовила варенье из слив. Белова – 38 лет, варила варенье из вишни; Краснова – 32 года, варила варенье из слив; Чернова – 41 год, варила варенье из яблок. 248. Родители Тани, Славы и Томы рассказывали в классе о своих профессиях, для того, чтобы помочь ребятам сделать выбор. Их фамилии Дьяков, Ершова и Громов. Они рассказали о профессии инженера, юриста и ученого. Определите, кто, о чем рассказывал, с учетом следующих сведений: 1) Танина мама выступала на 1 неделю позже инженера и на 4 недели позже Громова; 2) Лекция о профессии юриста была последней; 3) Томин папа – ученый. Танина мама рассказала о профессии юриста; родители Славы – о профессии инженера; Томин папа – о работе ученого. 249. Три девочки (Вера, Зоя и Наташа) едят мороженое. Одна из них взяла себе порцию, другая – две порции, а третья сразу три. При этом у одной из них мороженое красного цвета, у другой – белого, а у третьей – желтого. Определите, какого цвета мороженое было у них и какое количество порций взяла себе каждая из девочек, по следующим условиям:
2) Зоя ест белое мороженое; 3) У Веры порция больше, чем у той девочки, которая ест желтое мороженое, но меньше Зоиной порции. Вера съела 2 порции красного мороженого, Зоя 3 порции белого мороженого, Наташа – 1 порцию желтого мороженого. |