Современный этап реформирования экономического образования в России: тезисы

Вид материала

Содержание

Подобный материал:

1 2 3 4 5 6 7 8 9

26. Аппроксимационные свойства смешанных стратегий в играх со сравнимыми состояниями природы // Математика. Компьютер. Образование: Тезисы докладов и выступлений на X Международной конференции (г. Пущино, 20-25 января 2003 г.) / МОО «женщины в науке и образовании», Пущинский научный центр, Институт теоретической и экспериментальной биофизики РАН, Институт биофизики клетки РАН, Пущинский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Объединенный ин-т ядерных исследований (г.Дубна), Центральный экономико-математический ин-т РАН, Ин-т прикладной математики им. М. В. Келдыша, Ин-т философии РАН.-Москва-Ижевск: R&C Dynamics, 2003.-Выпуск 10.-С. 130.

Вводятся в рассмотрение игры со сравнимыми состояниями природы, в которых при поиске оптимальных стратегий по Обобщенному критерию Гурвица можно ограничиться только чистыми стратегиями. Изучаются аппроксимационные свойства смешанных стратегий в таких играх.

27. Игры со сравнимыми состояниями природы // Современные методы теории функций и смежные проблемы: Материалы конференции. Воронежская зимняя математическая школа (г. Воронеж, 26 января – 2 февраля 2003 г.) / Воронежский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Ин-т математики РАН им. В. А. Стеклова. – Воронеж: Воронежский гос. ун-т, 2003.-С.139-141.

Дается критерий игр со сравнимыми состояниями природы. Утверждается равенство цен игры в чистых и смешанных стратегиях. Сформулированы и доказаны критерий и достаточные условия оптимальности чистых стратегий по Обобщенному критерию Гурвица.

28. Игры со сравнимыми состояниями природы и маркетинг транспортных услуг // Транспорт: наука, техника, управление. -2003.-№ 2.-С. 7-13.

Рассмотрена задача определения транспортной фирмой оптимального уровня своих провозных возможностей с целью удовлетворения неизвестного спроса клиентов на транспортные услуги на планируемый период. Для решения этой задачи вводится в рассмотрение и используется класс игр со сравнимыми состояниями природы, в которых оптимальность чистых стратегий определяется Обобщенным критерием Гурвица.

29. Применение смешанных стратегий в игре со сравнимыми состояниями природы для принятия решений в маркетинге транспортных услуг // Транспорт: наука. техника, управление. -2003.-№ 4.-С. 18-28.

Для решения задачи, рассмотренной в работе под номером 27 настоящего списка, определяется Обобщенный критерий Гурвица относительно выигрышей для оптимальности смешанных стратегий. Изучаются аппроксимационные свойства смешанных стратегий. Находится приближенное смешанное решение задачи с наперед заданной точностью.

30. Применение критерия Гурвица к решению задачи об оптимальной покупке промышленными предприятиями газотурбинных двигателей для производства собственной электроэнергии // Консультант директора (Журнал для руководителя). -2003.-№ 22 (ноябрь).-С. 29-36.

Для решения задачи об оптимальной закупке промышленными предприятиями газотурбинных двигателей с целью производства собственной электроэнергии в качестве математической модели используется игра с природой размера 2х2, не являющаяся игрой со сравнимыми состояниями природы и в которой вероятности состояний природы не известны, Оптимальные стратегии определяются классическим критерием пессимизма-оптимизма Гурвица с показателем оптимизма

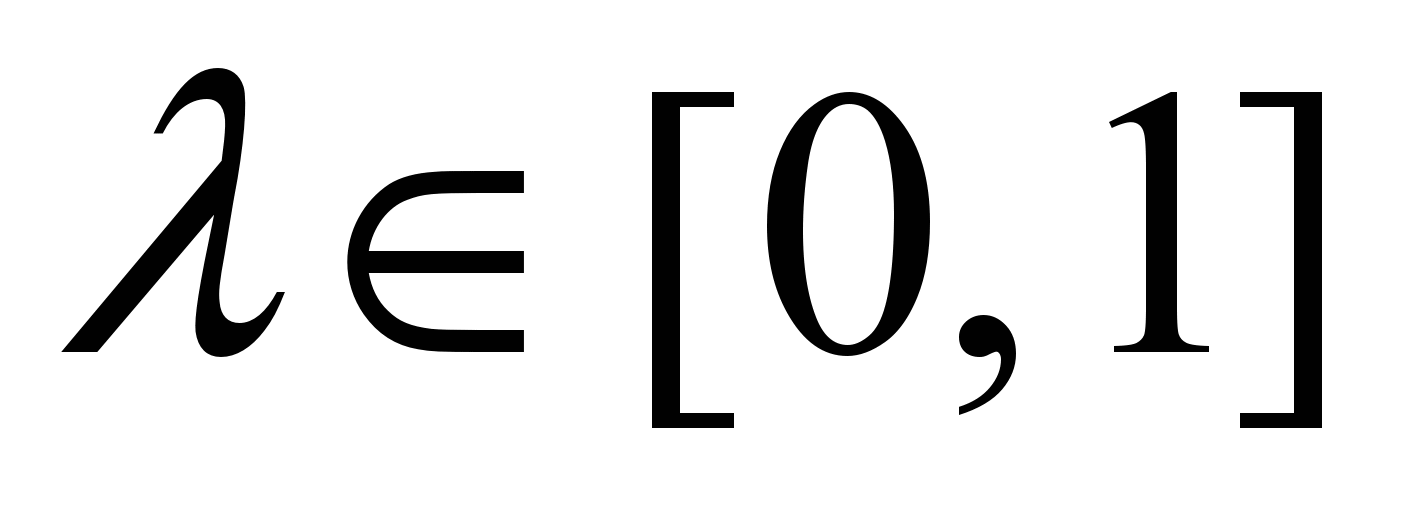. Дается полный анализ существования и нахождения оптимальных смешанных стратегий в зависимости от значения

.

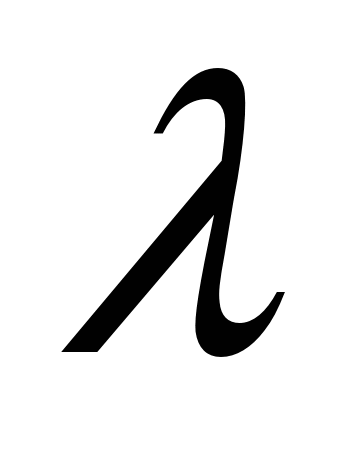31. О норме смешанной стратегии // Модели экономических систем и информационные технологии: Сборник научных трудов; Финансовая академия при Правительстве РФ. -М.: ФА, 2003.–Вып. XI.-С. 142 – 148.

Доказано существование смешанной стратегии с минимальной нормой. В терминах норм смешанных стратегий описываются чистые стратегии в классе всех смешанных стратегий и формулируется критерий того, что все чистые стратегии входят в смешанную стратегию с равными вероятностями.

32. Экономико-математическое моделирование. (Учебник. Гриф УМО. Авторские главы 2,5,6). - М.: ЭКЗАМЕН, 2004 г.-800 с. (В соавторстве с Абламской Л. В., Бабешко Л. О., Баусовым Л. И., Бывшевым В. А., Гриневой Н. В., Дрогобыцким И. Н., Ильинским А. И., Михеевым И. М., Серегиным Р. А).

Учебник подготовлен в соответствии с учебной программой по экономико-математическому моделированию, действующей в Финансовой академии при Правительстве РФ. Детально освещены вопросы методологии экономико-математического моделирования, теории игр, математического программирования, метод сетевого планирования, Марковские процессы и теория массового обслуживания, моделирование производственных процессов и сферы потребления, межотраслевые модели.

33. Теорема существования в игре с природой смешанной стратегии, оптимальной в смысле обобщенного критерия Гурвица // Компьютерное моделирование: Труды 5-й Международной научно-технической кон- ференции (29 июня - 3 июля 2004 г.) / Министерство образования РФ, Санкт-Петербургский гос. политехнический университет. - Санкт-Петербург, 2004.- Ч.1.-С. 55-64.

Доказано, что для любой игры с природой в любом замкнутом подмножестве множества смешанных стратегий существует стратегия, оптимальная в смысле Обобщенного критерия Гурвица относительно выигрышей. Отсюда в частности вытекает существование решения во множестве смешанных стратегий по Обобщенному критерию Гурвица относительно выигрышей.

34. Экономико-математическое моделирование. (Учебник. Электрон- ное издание.).-М.: Министерство РФ по связи и информатизации. ФГУП НТЦ «Информрегистр». Федеральный депозитарий электронных изданий, Ин-т открытого образования Финансовой академии при Правительстве РФ, 2004.-Номер государственной регистрации 0320400414.-CD-R(1ед.). (В соавторстве с Ланских А. Н., Жировым В. Ф.).

В учебнике освещен материал в соответствии с учебной программой по дисциплине «Экономико-математическое моделирование», действующей в Финансовой академии при Правительстве РФ.

35. Об оптимальных по критерию Байеса дублирующих стратегиях в играх с природой // Наука и образование в ВУЗе: направления и пути интеграции: Материалы I Межвузовской конференции по научно-исследовательской работе (27-28 июня 2005 г.) / Министерство образования и науки РФ, Федеральное агентство по образованию, Вятский гос. гуманитарный ун-т, Филиал в г. Ижевске. - Ижевск, 2005.- С.53-65.

Сформулировано и доказано необходимое и достаточное условие существования в игре с природой разных взаимно дублирующих смешанных стратегий, оптимальных по критерию Байеса относительно выигрышей. Дан алгоритм отыскания таких стратегий.

36. Анализ задачи страхования космических рисков с применением комбинированного критерия Гермейра-Гурвица // Вестник Финансовой академии, 2005.-№ 3.-С. 43-57. (В соавторстве со Штоховой И. Н.).

Рассмотрена задача о выборе страховой компанией оптимального метода страхования космических рисков при запуске объектов ракетно-космической техники. Для ее решения определяется на основе синтеза классических критериев Гермейера и Гурвица новый критерий оптимальности чистых стратегий в игре с Природой, названный комбинированным критерием Гермейера-Гурвица. В построенной модели состояния Природы предполагаются известными, и потому решение о выборе оптимальной стратегии принимается в условиях риска. Предложен новый метод вычисления показателя оптимизма лица, принимающего решение, основанный только на матрице Гермейера. Дается полное решение задачи для каждого значения показателя оптимизма страховой компании.

37. Выбор инвестиционного проекта по критерию Ходжа-Лемана. Часть 1. (Постановка задачи и формирование критерия) // Инновации и инвестиции (научно-аналитический журнал).-2005.-№6.-С. 29-44. (В соавторстве с Клюевым А. Н.).

Формулируется задача о выборе инвестором наиболее эффективного инвестиционного проекта при таких ограничениях, как срок окупаемости проекта, рентабельность проекта и др., которые ставит перед инвестором окружающая экономическая конъюнктура. В качестве математической модели выбрана игра с природой, в которой оптимальность стратегий определяется критерием Ходжа-Лемана. Дается подробное описание этого критерия относительно выигрышей и рисков для оптимальности чистых и смешанных стратегий. Решение принимается в условиях полунеопределенности, т. е. вероятности состояний природы известны, но лицо, принимающее решение, относится к ним с некоторой степенью доверия.

38. Геометрическая структура множества оптимальных по критерию Байеса смешанных стратегий в играх с природой // Современные проблемы прикладной математики и математического моделирования: Материалы Международной научной конференции (12-17 декабря 2005 г.)/Воронежская гос. технологическая академия, Воронежский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Воронежский областной ин-т повышения квалификации работников образования. - Воронеж: Воронежская гос. технологическая академия, 2005.-С.131.

Выявляется геометрическая структура множества смешанных стратегий, оптимальных во множестве смешанных стратегий по критерию Байеса относительно выигрышей.

39. Выбор инвестиционного проекта по критерию Ходжа-Лемана. Часть 2. (Математическая формализация и решение задачи)//Инновации и инвестиции (научно-аналитический журнал).-2006.-№ 7.-С.2-10. (В соавторстве с Клюевым А.Н.).

Дается математическая формализация задачи, поставленной в работе под номером 36 в этом списке, т. е. формируется реализационная структура модели игра с природой. Приводятся решения этой задачи в чистых и смешанных стратегиях по критерию Ходжа-Лемана относительно выигрышей и рисков на примере строительства элитного и доступного жилья Ленинградской области.

40. О существовании и алгоритме нахождения дублирующих смешанных стратегий в играх с природой// Актуальные проблемы математического моделирования в финансово-экономической области: Сборник научных статей; ФГОУВПО «Финансовая академия при Правительстве Российской Федерации».–М.: ФА, 2006.-Выпуск 6.-С.57-70.

Сформулировано и доказано необходимое и достаточное условие существования в игре с природой разных взаимно дублирующих смешанных стратегий. Дан алгоритм отыскания таких стратегий. Приведены примеры.

41. Критерий максимальной вероятности // Современные методы теории функций и смежные проблемы: Материалы Воронежской зимней математической школы / Воронежский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Математический ин-т им. В. А. Стеклова РАН.- Воронеж: Воронежский гос. ун-т, 2007.-С.124-125.

Определяются основные понятия критерия максимальной вероятности для оптимальности смешанных стратегий и проводится детальный анализ этого критерия.

42. О критерии Гермейера // Современные методы теории краевых задач: Материалы Воронежской весенней математической школы «Понтрягинские чтения - XVIII» / Воронежский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Математический ин-т им. В. А. Стеклова РАН.- Воронеж: Воронежский гос. ун-т, 2007.-С. 104-105.

Определяется и анализируется критерий Гермейера относительно выигрышей для оптимальности стратегий в непустом замкнутом подмножестве множества всех смешанных стратегий.

43. Применение модели “Игра с природой” с критериями оптимальности относительно рисков для анализа задачи эффективности утилизации атомных подводных лодок//Управление риском.- 2007.- № 3.-С. 11-20.

Решается задача определения приоритетного порядка реализации мероприятий по снижению риска возможных ядерных и радиационных аварий пр утилизации атомных подводных лодок с использованием математической модели «Игра с природой», в которой оптимальность определяется критериями относительно рисков: Байеса, Лапласа, Сэвиджа, Ходжа-Лемана, Гермейера, произведений, миниминного, Гурвица, максимальной вероятности и Обобщенного критерия Гурвица.

44. Обобщенный критерий пессимизма-оптимизма Гурвица оптимальности стратегий в играх с природой//В кн. Дрогобыцкий И. Н. Системный анализ в экономике.–М.:Финансы и статистика, 2007.- Приложение 10.-С. 393-442.

Дано подробное определение Обобщенного критерия Гурвица относительно выигрышей и рисков для оптимальности чистых и смешанных стратегий. Определены показатели пессимизма и оптимизма статистика. Предложен математико-формализованный метод выбора коэффициентов Обобщенного критерия Гурвица для чистых и смешанных стратегий. Доказана теорема существования решения в смешанных стратегиях. Определяются игры со сравнимыми состояниями природы. Приведены примеры.

45. Некоторые замечания о критерии Вальда// Современные проблемы прикладной математики и математического моделирования: Материалы II Международной научной конференции (г. Воронеж, 11-16 декабря 2007 г.) / Воронежская гос. технологическая академия, Воронежский гос. ун-т, Воронежский гос. технический ун-т, Московский гос. ун-т им. М. В. Ломоносова, Воронежский областной ин-т повышения квалификации работников образования.-Воронеж: Воронежская гос. технологическая академия, 2007.-С. 110-111.

Детально изучены новые свойства критерия Вальда оптимальности стратегий в играх с природой.

46. Теория критериев оптимальности и экономические решения (Монография).-М.: КноРус, 2008.-744 с.

Монография посвящена оценочному аспекту теории игр с природой. Проведено глубокое исследование критериев оптимальности чистых и смешанных стратегий относительно выигрышей и относительно рисков при принятии решений в условиях риска, неопределенности и полунеопределенности. Рассмотрены критерии Байеса, Лапласа, относительных значений вероятностей состояний природы, максимальной вероятности, Гермейера, Вальда, Сэвиджа, Ходжа-Лемана, Гурвица, произведений, Гермейера-Гурвица, максимаксный и миниминный критерии, Обобщенный критерий Гурвица. Дано приложение рассмотренных критериев к решению задач оптимизации риска при утилизации атомных подводных лодок, выбора оптимального метода страхования космических рисков и оптимизации инвестиций в строительство жилья.

47. Комбинация критерия Гермейера и обобщенного критерия Гурвица для оптимальности чистых стратегий относительно выигрышей в играх с природой // Современные методы теории краевых задач: Материалы Воронежской весенней математической школы “Понтрягинские чтения – XIX” (г. Воронеж, 3-9 мая 2008 г.) / Воронежский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Математический институт им. В. А. Стеклова РАН.- Воронеж: ВГУ, 2008.-С. 123-124. (В соавторстве с Гулюгиным А. Н.).

В играх с природой вводится в рассмотрение новый комбинированный критерий оптимальности чистых стратегий во множестве чистых стратегий относительно выигрышей, представляющий собой результат применения Обобщенного критерия Гурвица относительно выигрышей к матрице Гермейера. Сформулированы теоремы о нижней и верхней границах цены игры в чистых стратегиях, о структуре множества оптимальных стратегий и о необходимом и достаточном условии оптимальности чистой стратегии.

48. О структуре множества чистых стратегий, оптимальных по критерию Гурвица относительно выигрышей // Математика. Экономика. Образование: XVI Международная конференция (27 мая – 3 июня 2008 г. База отдыха «Моряк» Новороссийского морского пароходства) / Тезисы докладов / Министерство образования и науки, Московский гос. ун-т им. М. В. Ломоносова, Математический ин-т им. В. А. Стеклова РАН, Московский физико-технический ин-т (гос. ун-т), Южный Федеральный ун-т, Ростовский гос. экономический ун-т (РИНХ), МОО “Женщины в науке и образовании”, НОУ “Учебный центр “Знание”. – Ростов-на-Дону: Южный Федеральный ун-т, 2008.-С. 186-187.

Проведен анализ с формулировкой некоторых новых утверждений о структуре множества чистых стратегий, оптимальных по критерию Гурвица относительно выигрышей.

49. Комбинация критерия Гермейера и обобщенного критерия Гурвица для оптимальности чистых стратегий относительно выигрышей в играх с природой//Управление риском, 2008.-№2(46).-С.43-52. (В соавторстве с Гулюгиным А. Н.).

Приводятся подробные доказательства результатов, анонсированных в тезисах под номером 47 в настоящем списке.

50. О критерии максимальной вероятности для оптимальности стратегий в играх с природой // Актуальные проблемы математического моделирования в финансово-экономической области: Сборник научных статей; ФГОУВПО «Финансовая академия при Правительстве РФ».-М.:ФА,2008.-Выпуск 7.-С. 74-87.

Определяются основные понятия принципа максимальной вероятности в общем виде и проводится его детальный анализ для смешанных стратегий в играх с природой. При этом оптимальность стратегий рассматривается с точки зрения выигрышей статистика. Доказаны теорема существования оптимальной стратегии, равенство цен игры в чистых и в смешанных стратегиях, критерий оптимальности стратегии, а также теорема о структуре множества оптимальных смешанных стратегий. Приведены примеры.

51. Анализ коммерческой стратегии при неопределенной конъюнктуре с помощью обобщенного критерия Гурвица с формализовано выбранными коэффициентами//Стабилизация экономического развития Российской Федерации: VII Международная научно-практическая конференция (г. Пенза, октябрь 2008 г.). Сборник статей/Министерство образования и науки РФ, Международная академия инвестиций, Самарский гос. экономический ун-т, Нижегородский гос. техн. ун-т, Межотраслевой научно-информационный центр Пензенской гос. сельскохозяйственной академии. - Пенза, 2008.-Ч.1.-С.279-287.

Приведена задача о выборе оптимальной коммерческой стратегии при неопределенной конъюнктуре, в которой классический критерий Гурвица с любым показателем оптимизма

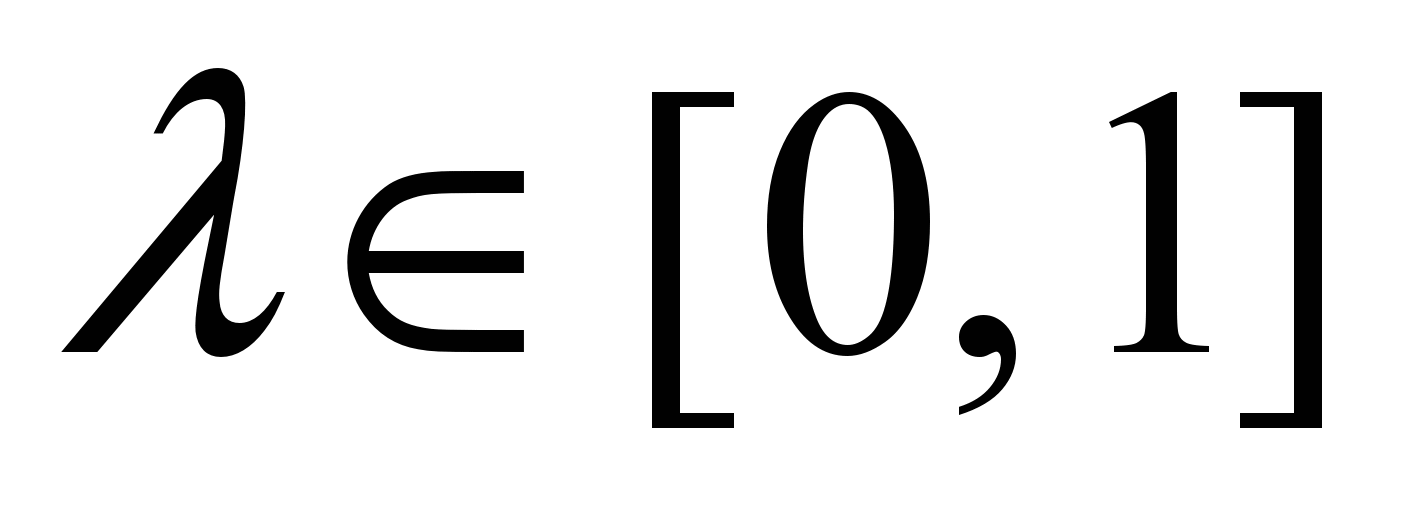не исполняет основной своей роли сглаживания экстремальностей - крайнего пессимизма критерия Вальда и крайнего оптимизма максимаксного критерия. Применяется к указанной задаче Обобщенный критерий Гурвица с формализовано выбранными коэффициентами по различным принципам и формулам.

Михалева Мария Юрьевна

1. Применение методов многокритериальной оптимизации при формировании портфеля инвестиционных проектов [Электронный ресурс] // Ломоносов-2005: Сборник тезисов докладов на Международной конференция студентов, аспирантов и молодых учёных (12 – 15 апреля 2005 г.) / МГУ им. М. В. Ломоносова.- М.: МГУ им. М. В. Ломоносова, 2005.-Т. 1.-С. 176 – 177.

Представлены принципы формирования оптимального портфеля инвестиционных проектов и предпосылки математического моделирования портфеля в рамках многокритериального подхода.

2. Алгоритмы многокритериального выбора в задаче формирования портфеля инвестиционных проектов // Актуальные проблемы математического моделирования в финансово-экономической области: Сборник научных статей; ФГОУ ВПО «Финансовая академия при Правительстве Российской Федерации». – М.: ФА, 2006. – Вып. 6. – С. 83 – 96.

Представлена математическая постановка задачи многокритериальной оптимизации портфеля, проанализированы и описаны алгоритмы многокритериального отбора проектов. Алгоритмы могут быть использованы в процессе формирования оптимального портфеля инвестиционных проектов.

3. Обобщенная модель портфеля инвестиционных проектов в формате концепции комплексного инвестиционного проектирования // Современные методы теории функций и смежные проблемы: Материалы Воронежской зимней математической школы / Воронежский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Математический ин-т им. В. А. Стеклова РАН.- Воронеж: Воронежский гос. ун-т, 2007. – С. 155 – 156.

Разработана модель оптимизации инвестиционного портфеля как системы, элементами которой являются проекты, объединенные единой стратегией предприятия и направленные на решение различных долго-, средне- и краткосрочных задач.

4. Модель оптимизации портфеля инвестиционных проектов в формате концепции комплексного инвестиционного проектирования [Электронный ресурс] // Ломоносов: Материалы XIV Международной конференции студентов, аспирантов и молодых ученых / Факультет журналистики.–М.: Издательский центр Факультета журналистики МГУ им. М. В. Ломоносова.- 2007. – 1 электрон. опт. диск (CD ROM).

Рассмотрен обобщенный портфель инвестиционных проектов, включающий основные и вспомогательные проекты. Вспомогательные проекты подразделяются на проекты-доноры и проекты-акцепторы. Основные проекты выполняют долгосрочные задачи высокой значимости для предприятия, вспомогательные проекты решают тактические задачи финансового обеспечения.

5. Многоступенчатая динамическая модель оптимизации портфеля коммерческих и некоммерческих инвестиционных проектов // Современные проблемы прикладной математики и математического моделирования: Материалы II Международной научной конференции (г. Воронеж, 11-16 декабря 2007 г.) / Воронежская гос. технологическая академия, Воронежский гос. ун-т, Воронежский гос. технический ун-т, Московский гос. ун-т им. М. В. Ломоносова, Воронежский областной ин-т повышения квалификации работников образования.- Воронеж: Воронежская гос. технологическая академия, 2007.- С. 134 – 135.

Построена модель оптимизации инвестиционного портфеля, включающего как коммерческие, так и некоммерческие проекты. Для решения задачи используется алгоритм многоступенчатой динамической оптимизации.

6. Портфель инвестиционных проектов как объект моделирования // Вестник Финансовой академии. – М., 2008. – № 1(45). – С. 176 – 180.

Рассмотрены основополагающие принципы формирования портфеля инвестиционных проектов: многокритериальность отбора проектов в портфель, дифференциация критериев отбора по типам инвестиционных проектов, учёт объективных ограничений инвестиционной деятельности предприятия.

Blog

Содержание