Бабешко Людмила Олеговна. Об одном неравенстве и его использовании в теории массового обслуживания // Современный этап реформирования экономического образования в России: тезисы
| Вид материала | Тезисы |
СодержаниеКружилов Сергей Иванович Лабскер Лев Григорьевич |
- Задачи теории массового обслуживания. Классификация систем массового обслуживания, 38.01kb.
- Введение в теорию массового обслуживания, 10.41kb.
- Задачи теории массового обслуживания (тмо). Типы систем массового обслуживания (смо), 95.6kb.
- Утверждаю, 89.56kb.
- Компьютерное моделирование массового обслуживания клиентов на фармацевтическом рынке, 202.1kb.
- Основные сведения из теории массового обслуживания, 47.41kb.
- Системы массового обслуживания, 754.03kb.
- Рабочей программы дисциплины «Введение в теорию систем массового обслуживания» по направлению, 20.17kb.
- Содержание занятия «Модели массового обслуживания», 547.79kb.
- Оценка эффективности реструктуризации предприятия, 54.64kb.
19. Прикладные проблемы радиационной теплофизики в гляциологии //Тр. высокогорного геофизич. Ин-та, Госкомгидро-мет, 2006-С. 34-44. (В соавторстве с Мерзликиным В. Г. и др.). Разработана классификация прикладных проблем теплофизики снежных и ледовых массивов, актуальная при исследовании процессов их тепло- и массообмена с окружающей средой, а также вопросов их устойчивости. 20. Математика в экономике. Основы математики (Учебник. Гриф Министерства образования РФ).-М.: ФБК-Пресс, 2005.-472с. Приведены все разделы математики, необходимые для высшего экономического образования. Представлено большое число задач с экономическим содержанием, имеется подборка упражнений для практических занятий. Учебник соответствует Госстандарту ВПО для экономических специальностей. 21. Математика для экономического бакалавриата (Учебник. Гриф УМО).-М.: Дело, 2005.- 576 с. (В соавторстве с Чупрыновым Б. П.). Представлена совокупность математических дисциплин, соответствующая государственному образовательному стандарту высшего профессионального образования направления "Экономика", степень - бакалавр экономики. 22. Математические методы и модели для магистрантов экономики (Учебник. Грифом УМО) –СПб.: Питер, 2006.-496 с. (В соавторстве с Чупрыновым Б. П.). Изложены основные математические методы и модели, необходимые в образовании магистрантов по направлению "Экономика": математическое программирование и эконометрика, эколого-экономические системы, финансовая математика, инфляция и государственный долг. 23. Лучистая инверсия температурного поля в снежных покровах высокогорных ледников //-М.: МГИ, Хроника, обсуждения. -Вып.117, Наука, 2007.-С.113-118. (В соавторстве с Мерзликиным В. Г., Гутиэррес-Охеда М., и Аджиевым И.). Приведены сравнения расчетных и температурных профилей верхних слоев снега и льда на ледниках и их внутрисуточные изменения в условиях высокогорья. 24. Математика в экономике. Математические методы и модели (Учебник. Гриф Министерства образования РФ). - М.: Финансы и статистика, 2007. -542 с. (В соавторстве с Чупрыновым Б. П.). Изложены основы разделов прикладной математики: математической статистики, методов оптимизации, эконометрики. Представлены методы и модели, наиболее актуальные в современной экономике: расчеты рисков, финансовая математика, глобальные модели экономики. 25. Методы реинжиниринга и оптимизации в решении проблем экономики //Инновационные факторы во внешнеэкономической сфере России: Материалы конференции.-Ставрополь: АГРУС, 2008.-С.209-217. (В соавторстве с Приваловым А. И.). Разработана концепция и основная схема решения проблем экономики, имеющих системный характер. В ней воедино связаны методы реинжиниринга бизнес-процессов и многокритериальной оптимизации по ограниченному множеству допустимых сценариев. Кружилов Сергей Иванович 1. Технологии подготовки документов в среде текстового процессора Microsoft Word (Учебник. Гриф УМО). - М.: ФА, 2003.- 324 с. (В соавторстве с Нвежиным В. П.). Рассмотрены как теоретические, так и практические вопросы использования текстового процессора Microsoft Word при подготовке документов. Приводятся примеры подготовки отдельных компонент документа с соблюдением существующего ГОСТа. 2. Сборник задач по курсу «Экономико-математическое моделирование». - М.: Городец, 2005.- 320 с. (В соавторстве с Нвежиным В. П). В сборнике подобраны и систематизированы примеры и задачи по таким разделам курса Экономико-математическое моделирование, как: линейному, нелинейному и динамическому программированию, системам массового обслуживания, принятию решений и теории игр, моделям управления запасами, системам массового обслуживания, сетевому моделированию и др. 3. Системные принципы образования при подготовке специалистов // Системный анализ в проектировании и управлении: Труды XI Международной научно-практической конференции (г. Санкт-Петербург, 28 - 30 июня 2007 г.) - СПб.: Изд-во Политехнического ун-та, 2007. - Ч.3.- 315 с. (В соавторстве с Нвежиным В. П.). Обсуждаются вопросы системного подхода к обучению специалистов. Приводятся узкие места в образовательном процессе, в которых просто необходимо использовать системные подходы. 4. Организационные принципы социальных систем. // Системный анализ в проектировании и управлении: Труды XII Международной научно-практической конференции (г. Санкт-Петербург, 24 - 26 июня 2008 г.) - СПб.: Изд-во Политехнического ун-та, 2008. - Ч.1.- 324 с. (В соавторстве с Нвежиным В. П.). Рассматривается системный анализ правовых основ общества, в том числе приводится моделирование основных категорий правовой системы: власти, права и законов. Лабскер Лев Григорьевич 1. Математическое моделирование финансово-экономических ситуаций с применением компьютера (на основе Марковских случайных процессов) (Учебное пособие для проведения практических занятий. Издание 2-е, исправленное. Гриф УМО). – М.: Финансовая академия при Правительстве РФ. Кафедра математического моделирования экономических процессов, 1998.-226 с. (В соавторстве с Михайловой В. П. и Серегиным Р. А.). Изложены (без доказательств) основы теории дискретных Марковских процессов с дискретным и непрерывным временем и дана иллюстрация их приложения к моделированию различных финансово-экономических ситуаций с применением IBM PC. Предназначено для студентов, магистрантов и аспирантов финансовых и экономических специальностей ВУЗов, изучающих курс экономико-математического моделирования с исследованием операций. Может быть полезным для преподавателей, ведущих соответствующих курс, и специалистов, занимающихся вопросами устойчивости, прогнозирования и управления финансово-экономическими процессами. 2. Об одном неравенстве и его использовании в теории массового обслуживания // Современный этап реформирования экономического образования в России: Тезисы докладов и выступлений на Международной учебно-методической конференции (25-27 марта 1998 г.) / Финансовая академия при Правительстве РФ.-М.: ФА, 1998.–Ч.4.-С. 200-202 (В соавторстве с Бабешко Л. О.). Дается краткое объяснение доказательства неравенства 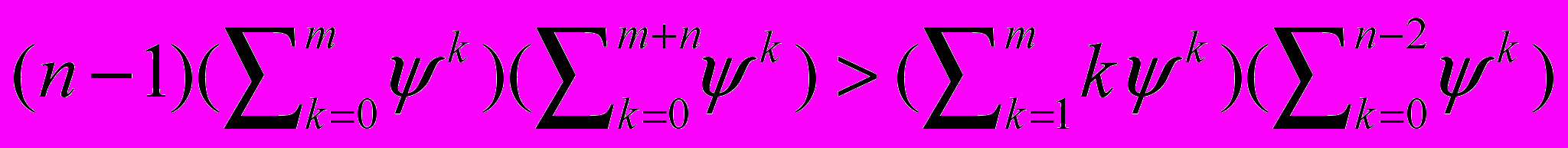 , ,где 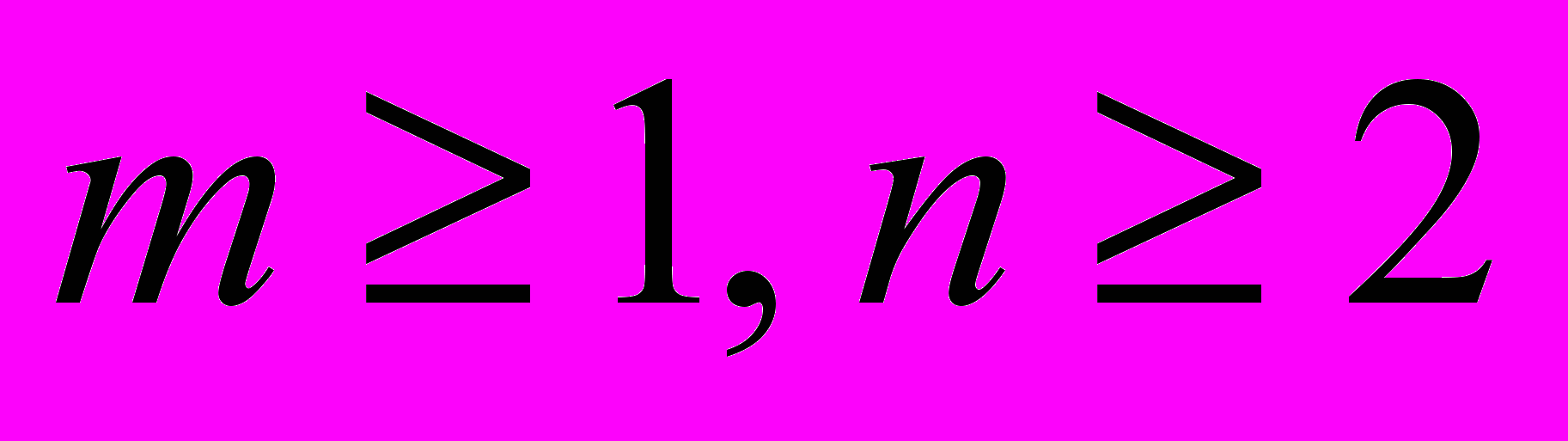 - произвольные натуральные числа, а - произвольные натуральные числа, а 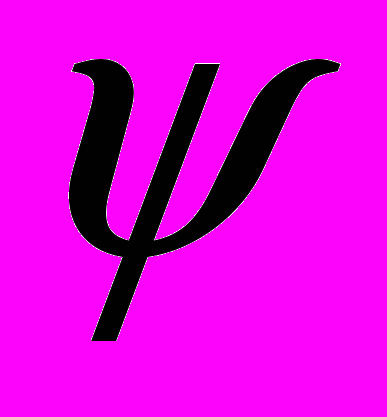 - любое положительное число. Это неравенство может быть использовано в теории массового обслуживания при доказательстве того, что среднее время пребывания заявки в системе при взаимопомощи между каналами меньше среднего времени пребывания заявки в системе без взаимопомощи. - любое положительное число. Это неравенство может быть использовано в теории массового обслуживания при доказательстве того, что среднее время пребывания заявки в системе при взаимопомощи между каналами меньше среднего времени пребывания заявки в системе без взаимопомощи.3. Теория массового обслуживания в экономической сфере. (Учебное пособие. Рекомендательный гриф Министерства общего и профессионального образования РФ).– М.: “Банки и биржи”, Издательское объединение ЮНИТИ, 1998.-320 с. (В соавторстве с Бабешко Л.О.). Рассмотрены основы теории массового обслуживания, ее применение в моделировании система массового обслуживания в различных областях экономики, проанализированы простейшие системы, в которых протекает Марковский процесс «гибели и размножения». Представлены тексты разработанных программ, позволяющие использовать при решении задач персональный компьютер. Для студентов, магистрантов и аспирантов, изучающих в вузах курс экономико-математического моделирования. 4. О математической интерпретации понятия отдачи производственной функции от расширения масштаба производства//Научные основы преподавания финансово-кредитных и учетных дисциплин: Тезисы докладов и выступлений на Международной научно-методической конференции (г. Москва, 22-24 марта 1999 г.)/Финансовая академия при Правительстве РФ.-М.:ФА,1999.-Ч. IV.-С.217-219. Пусть 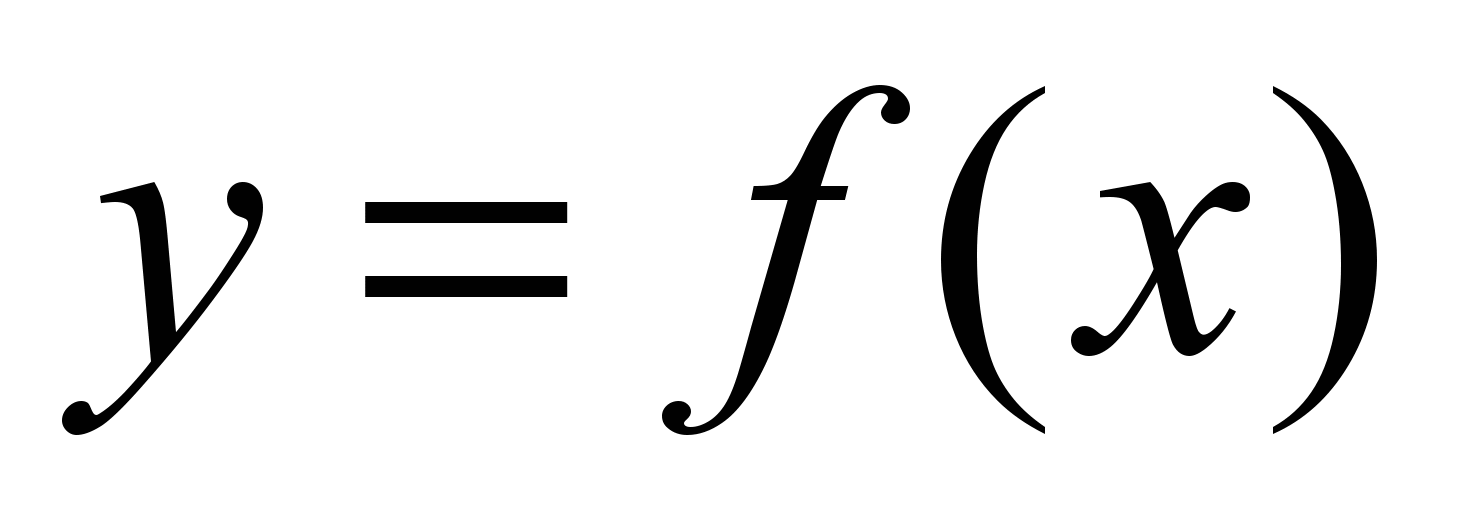 - производственная функция выпуска продукции, где - производственная функция выпуска продукции, где 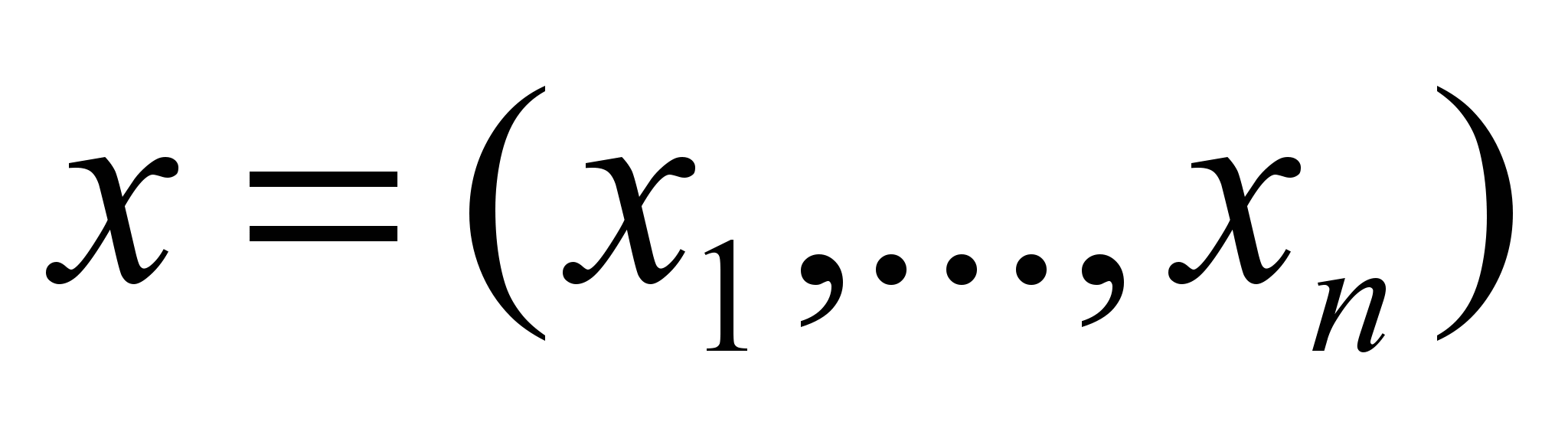 - - 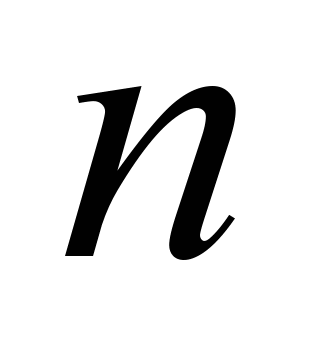 -мерный вектор затрачиваемых в производстве -мерный вектор затрачиваемых в производстве 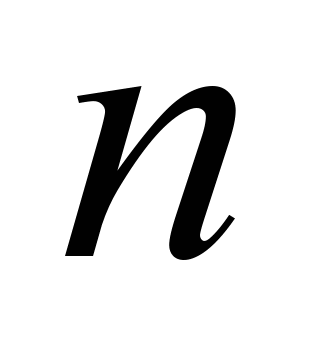 видов ресурсов в количествах соответственно видов ресурсов в количествах соответственно 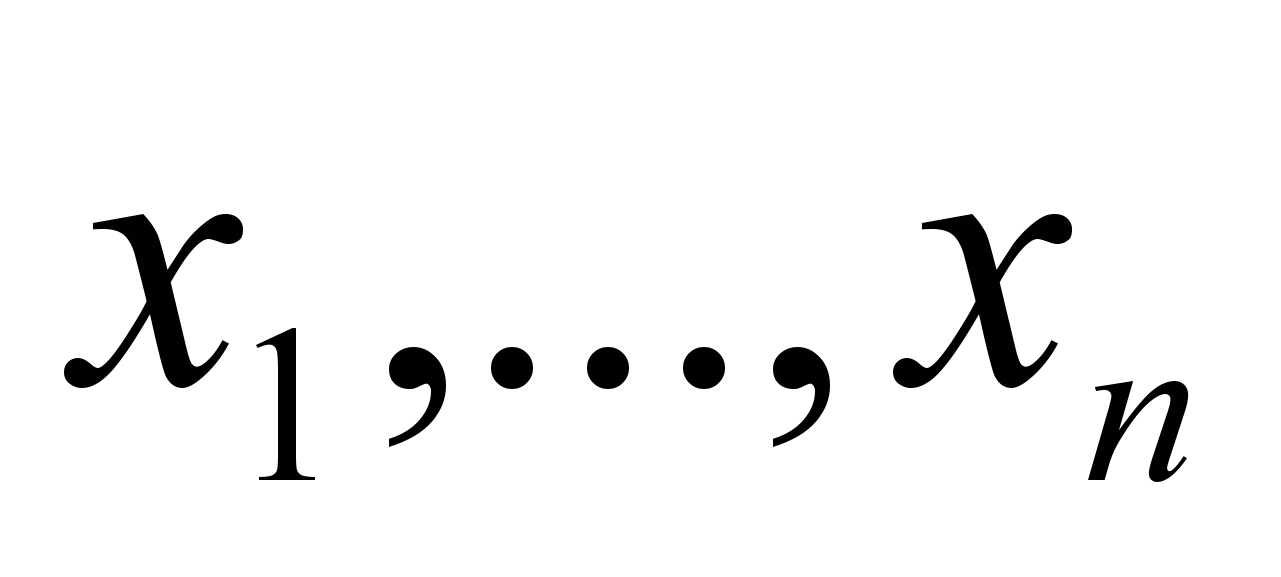 , а , а 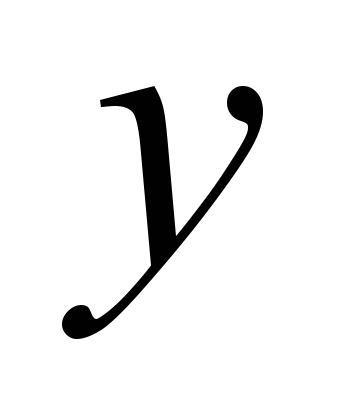 -скалярная величина, обозначающая объем выпускаемой продукции. Отдача производственной функции -скалярная величина, обозначающая объем выпускаемой продукции. Отдача производственной функции 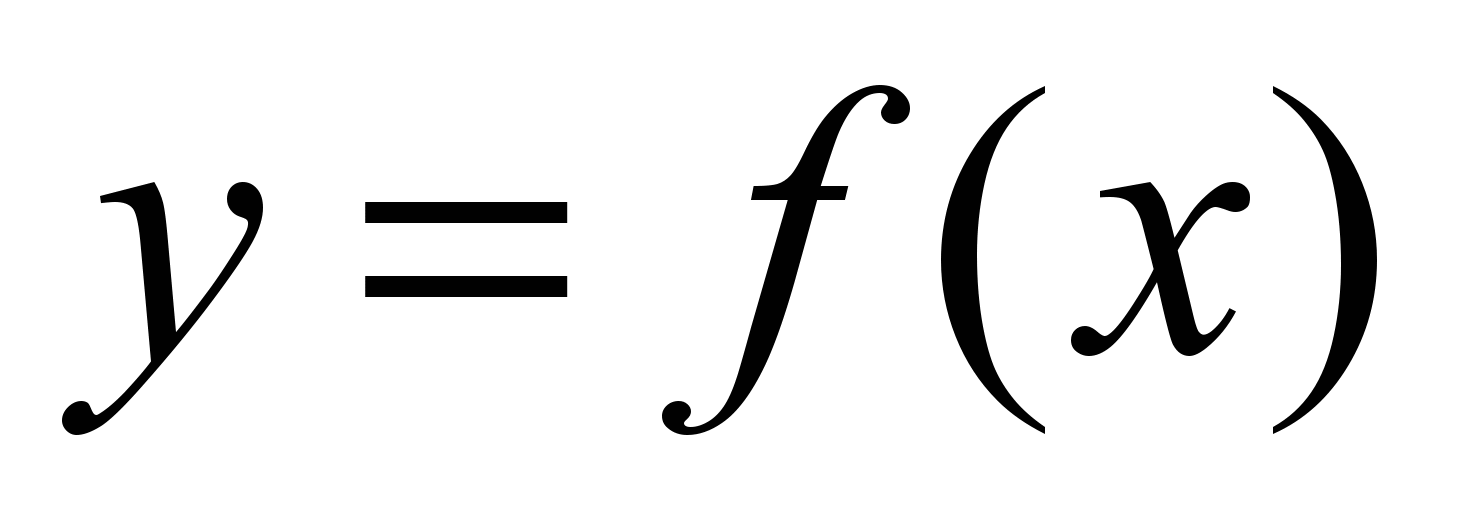 в зависимости от масштаба затрат в зависимости от масштаба затрат 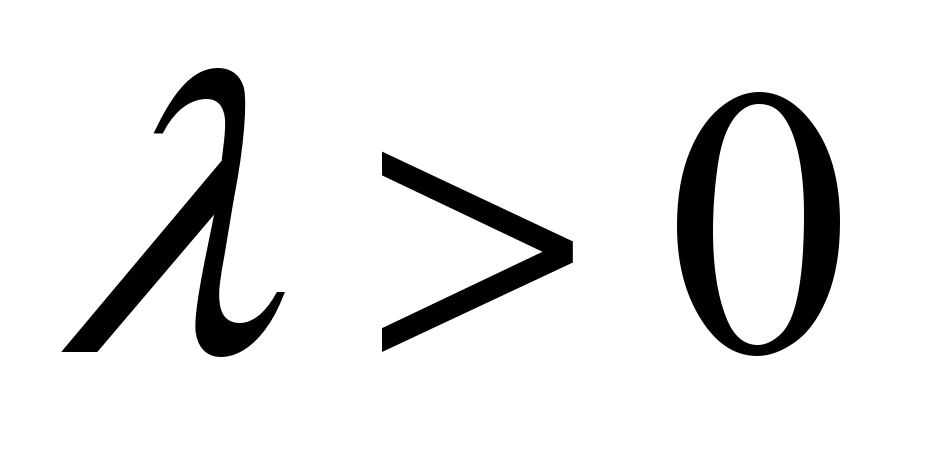 определяется как функция определяется как функция 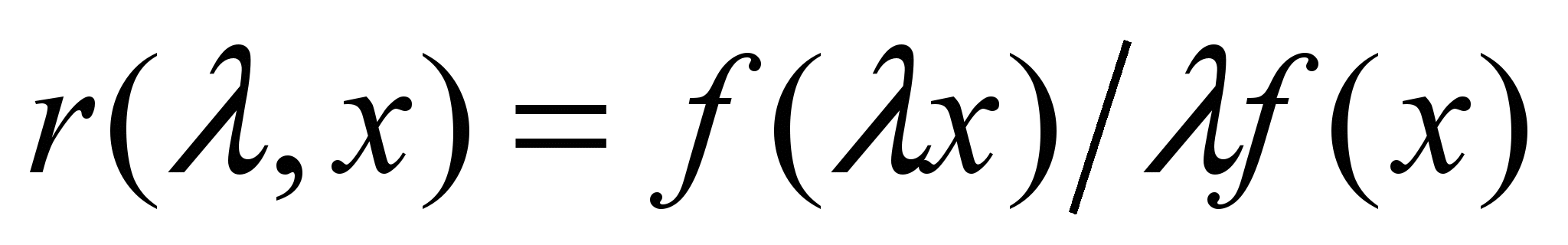 . . 5. О среднем времени пребывания заявки в системе массового обслуживания//Актуальные проблемы математического моделирования в финансово-экономической области: Сб. научных статей; Финансовая академия при Правительстве РФ. Кафедра математического моделирования экономических процессов.–М.:ФА,1999.-С.3-10.( В соавторстве с Бабешко Л. О.). Дано подробное аналитическое доказательство тому, что среднее время пребывания заявки в многоканальной СМО с отказами и равномерной взаимопомощью между каналами меньше среднего времени пребывания заявки в СМО без взаимопомощи. 6. О влиянии равномерной взаимопомощи между каналами на среднее время пребывания заявки в многоканальной системе массового обслуживания // XXI век: новая модель специалиста-экономиста: Тезисы докладов на Международной научно-методической конференции (г. Москва, 28-30 марта 2000 г.) / Москва, Финансовая академия при Правительстве РФ.- М.: ФА, 2000.-Часть 5.-С. 143-147. (В соавторстве с Бабешко Л. О.). Сформулировано утверждение о том, что равномерная взаимопомощь между каналами в многоканальной СМО с ожиданием и ограничением на длину очереди уменьшает среднее число заявок в очереди, среднее число заявок под обслуживанием и, следовательно, уменьшает среднее время ожидания заявки в очереди и среднее время обслуживания заявки. 7. Обобщенный критерий пессимизма-оптимизма Гурвица // XXI век: новая модель специалиста-экономиста: Тезисы докладов на Международной научно-методической конференции (г. Москва, 28-30 марта 2000 г.) / Москва, Финансовая академия при Правительстве РФ.-М.: ФА, 2000.-Часть 5.-С.148-151. Определяется новый критерий, названный Обобщенным критерием Гурвица оптимальности чистых стратегий относительно выигрышей, позволяющий выбирать оптимальные стратегии в условиях полной неопределенности, учитывающий все выигрыши при каждой чистой стратегии и обобщающий критерий Вальда, максимаксный критерий и классический критерий Гурвица. Предложен формализованный метод выбора коэффициентов этого критерия. 8. О влиянии равномерной взаимопомощи между каналами на среднее время пребывания заявки в многоканальной системе массового обслуживания // Качество информационных услуг: Сб. научных трудов; Министерство образования РФ, Финансовая академия при Правительстве РФ, Московский гос. ун-т коммерции, Тамбовский гос. техн. университет.-Тамбов: ТГТУ, 2000.-Вып. III.-С. 43-52 (В соавторстве с Бабешко Л. О.). Дано развернутое изложение вместе с доказательствами результатов, анонсированных в тезисах под номером 6 в настоящем списке. 9. Обобщенный критерий пессимизма-оптимизма Гурвица // Качество информационных услуг: Сб. научных трудов; Министерство образования РФ, Финансовая академия при Правительстве РФ, Московский гос. ун-т коммерции, Тамбовский гос. техн. университет.-Тамбов: ТГТУ, 2000.-Вып. III.-С. 34-43. Даны полные доказательства результатов, анонсированных в тезисах под номером 7 в настоящем списке. 10. О некоторой общей схеме формирования критериев оптимальности в играх с природой // Вестник Финансовой академии, 2000.-№ 2.-С. 61-76. Предложена общая схема формирования критериев оптимальности чистых стратегий в играх с природой. На основе этой схемы выделены некоторые классы критериев, которые, с одной стороны, включают в себя в качестве частных случаев известные классические критерии такие, как критерии Вальда, Сэвиджа, Гурвица и др., а с другой стороны, дают возможность формировать новые критерии. Устанавливается эквивалентность некоторых из рассмотренных критериев. Приведен пример нахождения оптимальных стратегий по рассмотренным критериям. 11. Об одном неравенстве и его использовании в теории массового обслуживания // Актуальные проблемы математического моделирования в финансово-экономической области; Сб. научных статей; Финансовая академия при Правительстве РФ. – М.: ФА, 2000.-С.3-15. (В соавторстве с Бабешко Л. О.). Дано подробное доказательство справедливости неравенства, анонсированного в тезисах под номером 2 в настоящем списке. 12. Обобщенный критерий пессимизма-оптимизма Гурвица // Финансовая математика (Коллективная монография): Московский гос. ун-т им. М. В. Ломоносова, Экономический факультет, Центр общественных наук.-М.: МГУ им. М. В. Ломоносова, 2001.-С. 401-414. Предложен критерий выбора оптимальной стратегии в условиях полной неопределенности учитывающий все выигрыши лица, принимающего решение, при каждой возможной его стратегии. Предложенный критерий обобщает критерий крайнего пессимизма Вальда, критерий крайнего оптимизма и критерий пессимизма-оптимизма Гурвица. Предложен метод выбора коэффициентов, основанный на принципе «невозрастания средних выигрышей» в случае опасной ситуации и на принципе «неубывания средних выигрышей» в случае ситуации благоприятной. Приведен пример из финансовой области. 13. Обобщенный критерий Гурвица относительно рисков. // Современные методы в теории краевых задач. “Понтрягинские чтения - XII”: Тезисы докладов. Воронежская весенняя математическая школа (3-9 мая 2001 г.)/Воронежский гос. ун-т, Московский гос. ун-т им. М. В. Ломоносова, Институт математики РАН им. В. А. Стеклова.–Воронеж: Воронежский гос. ун-т, 2001.-С.101-102. Основные идеи оптимальности стратегий в играх с природой по Обобщенному критерию Гурвица относительно выигрышей распространяются на Обобщенный критерий Гурвица относительно рисков. 14. Обобщенный критерий пессимизма-оптимизма Гурвица относительно рисков. Часть 1 // Управление риском, 2001.- № 2.-С. 35-37. Определяется новый критерий оптимальности чистых стратегий относительно рисков, названный Обобщенным критерием Гурвица. Вводятся в рассмотрение коэффициенты этого критерия, на основе которых определяются количественные показатели оптимизма и пессимизма лица, принимающего решение. Предлагается математико-формализованный выбор указанных коэффициентов. 15. Обобщенный критерий пессимизма-оптимизма Гурвица относительно рисков. Часть 2 // Управление риском, 2001.-№ 3.-С. 16-20. Приводятся частные случаи предложенного Обобщенного критерия Гурвица относительно рисков, который при соответствующих значениях коэффициентов превращается в критерии Байеса, Лапласа относительно рисков, в классический критерий Гурвица относительно рисков, а также в критерий Сэвиджа и миниминный критерий. Приведен пример инвестирования средств в покупку акций. 16. Об одной модели стоимостной функции объекта недвижимости // Московский оценщик, 2001.-№ 5.-С. 39-53 (В соавторстве с Румянцевым С. И.). Статья посвящена одному из методов построения стоимостной функции массовой оценки объектов недвижимости. Аргументом этой функции является объект недвижимости, определяемый количественными значениями выбранных характеристик, а значением – его стоимость. В основе построения указанной функции лежат ценообразующие факторы, коэффициенты их значимости и понятие интерполяционной функции. Приведен пример массово оценки объектов жилого фонда. 17. Обобщенный критерий Гурвица относительно рисков для принятия оптимальных решений в условиях неопределенности // Современные образовательные технологии подготовки специалистов-экономистов в вузах России: Тезисы докладов и выступлений на Международной научно - методической конференции (Москва, 27-30 марта 2001 г.) / Финансовая академия при Правительстве РФ.– М.: ФА, 2001.-Ч. 4.-С. 177-181. В играх с природой для оценивания оптимальности стратегий с точки зрения рисков определяется Обобщенный критерий Гурвица относительно рисков. Приводятся примеры. 18. Стоимостная функция объектов недвижимости // Современные образовательные технологии подготовки специалистов- экономистов в вузах России: Тезисы докладов и выступлений на Международной научно- методической конференции (Москва, 27-30 марта 2001 г.) / Финансовая академия при Правительстве РФ. – М.: ФА, 2001.-Ч.4.-С. 182-187. (В соавторстве с Румянцевым С.И.). Определяется некоторая стоимостная функция для массовой оценки объектов недвижимости. Приводится пример оценки стоимости квартир. 19. Игровые методы в управлении экономикой и бизнесом. (Учебное пособие. Гриф УМО). -М.: ДЕЛО, 2001.-465 с. (В соавторстве с Бабешко Л. О.). Излагаются основы теории игр, охватывающие вопросы принятия оптимальных решений в условиях антагонистической конкуренции, риска и неопределенности. Иллюстрируется их применение в качестве математических моделей различных задач из области экономики, финансов и бизнеса. Приведено большое количество разобранных примеров и упражнений с ответами. Предназначается для студентов, обучающихся по специальностям финансово-экономического направления, магистрантов и аспирантов. Может быть полезной преподавателям, ведущим курс экономико-математических моделей и методов, а также различным специалистам, желающим познакомиться с основами игровых методов в управлении экономикой и бизнесом. 20. Вероятностное моделирование в финансово-экономической области. (Учебное пособие. Гриф Министерства образования РФ). - М.: Альпина Паблишер, 2002.-224 с. Изложены основы теории Марковских процессов, протекающих в дискретных системах с дискретным и непрерывным временем. Иллюстрируется их применение в качестве вероятностных моделей различных финансово-экономических ситуаций. Приведено достаточное количество детально разобранных примеров и заданий с ответами для самостоятельной работы читателя. Адресовано студентам очной, заочной и очно-заочной форм обучения, магистрантам, аспирантам и слушателям институтов профессиональной подготовки по специальностям финансово-экономического направления. Может оказаться полезным преподавателям, ведущим лекционные курсы и практические занятия по дисциплине экономико-математического моделирования. 21. Обобщенный критерий Гурвица оптимальности смешанных стратегий относительно выигрышей // Финансовый Менеджмент, 2002.-№ 2.- С. 57-66. ссылка скрытаk Определяется Обобщенный критерий Гурвица оптимальности смешанных стратегий относительно выигрышей. Предлагается формализованный выбор коэффициентов рассматриваемого критерия. Приведен пример из финансовой области. 22. Сплайн-интерполяционная модель стоимостной функции объектов недвижимости // Московский оценщик, 2002.-№ 2 (15), апрель.-С. 10-25. (В соавторстве с Румянцевым С. И.). Построена сплайн-интерполяционная модель, которая реализует кусочно-линейное представление стоимостной функции массовой оценки недвижимости. Предложенная модель удовлетворяет естественным экономическим требованиям и обеспечивает адекватные вычисления стоимости объектов недвижимости. 23. Об одном формализованном методе выбора коэффициентов Обобщенного критерия Гурвица оптимальности смешанных стратегий в условиях неопределенности // Модели экономических систем и информационные технологии: Сборник научных трудов / Финансовая академия при Правительстве РФ. - М.: ФА, 2002.- Вып. VI.-С. 139 – 146. Определяется Обобщенный критерий Гурвица оптимальности стратегий в произвольном подмножестве  множества смешанных стратегий, которое в частности может быть множеством чистых стратегий или множеством всех смешанных стратегий. Выбор оптимальной стратегии происходит в условиях неопределенности. Для конечного множества множества смешанных стратегий, которое в частности может быть множеством чистых стратегий или множеством всех смешанных стратегий. Выбор оптимальной стратегии происходит в условиях неопределенности. Для конечного множества  определяется формализованный метод выбора коэффициентов Обобщенного критерия Гурвица. определяется формализованный метод выбора коэффициентов Обобщенного критерия Гурвица. 24. Общая методика конструирования критериев оптимальности решений в условиях риска и неопределенности // Финансовый менеджмент, 2002.-№ 5.-С. 58-74. (В соавторстве с Яновской Е. В.). Описывается модифицированный матрично-векторный подход к построению критериев оптимальности стратегий относительно выигрышей в статистических играх, обобщающий принципы конструирования известных критериев. Приложение рассмотренных критериев дается на примере принятия решения инвестором о строительстве жилья определенного типа в определенном месте. 25. Общая методика конструирования критериев оптимальности решений в условиях риска и неопределенности // Управление риском, 2002.- № 4.-С. 13-24. (В соавторстве с Яновской Е. В.) Предложена общая методика формирования критериев для принятия решений в условиях риска и неопределенности, оптимальных с точки зрения выигрышей лица, принимающего решение. Описанная методика включает в себя в качестве частных случаев методики конструирования критериев Байеса, Лапласа, Вальда, Ходжа-Лемана, Гермейера, Гурвица, а также критерия произведений, максимаксного критерия и Обобщенного критерия Гурвица. Приведен пример из финансовой области. |
