Бабешко Людмила Олеговна. Об одном неравенстве и его использовании в теории массового обслуживания // Современный этап реформирования экономического образования в России: тезисы
| Вид материала | Тезисы |
- Задачи теории массового обслуживания. Классификация систем массового обслуживания, 38.01kb.
- Введение в теорию массового обслуживания, 10.41kb.
- Задачи теории массового обслуживания (тмо). Типы систем массового обслуживания (смо), 95.6kb.
- Утверждаю, 89.56kb.
- Компьютерное моделирование массового обслуживания клиентов на фармацевтическом рынке, 202.1kb.
- Основные сведения из теории массового обслуживания, 47.41kb.
- Системы массового обслуживания, 754.03kb.
- Рабочей программы дисциплины «Введение в теорию систем массового обслуживания» по направлению, 20.17kb.
- Содержание занятия «Модели массового обслуживания», 547.79kb.
- Оценка эффективности реструктуризации предприятия, 54.64kb.
Аннотированные научные публикации
профессорско-преподавательского состава кафедры
за период с 1998 года по 2008 год.
Бабешко Людмила Олеговна.
1. Об одном неравенстве и его использовании в теории массового обслуживания // Современный этап реформирования экономического образования в России: Тезисы докладов и выступлений на Международной учебно-методической конференции (25-27 марта 1998 г.) / Финансовая академия при Правительстве РФ.-М.: ФА, 1998.–Ч.4.-С. 200-202 (В соавторстве с Лабскером Л. Г.).
Дается краткое объяснение доказательства неравенства
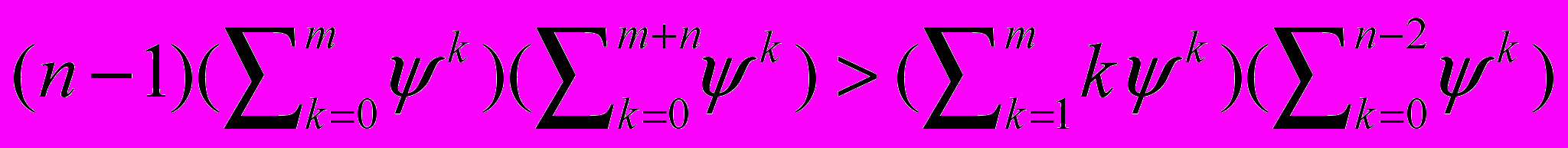,где
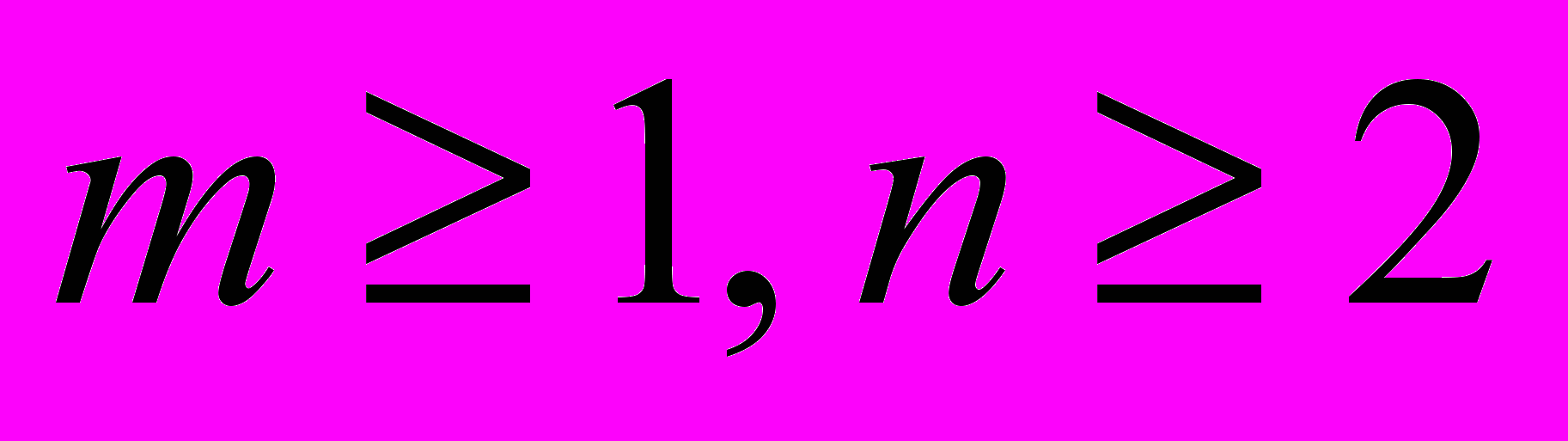- произвольные натуральные числа, а 
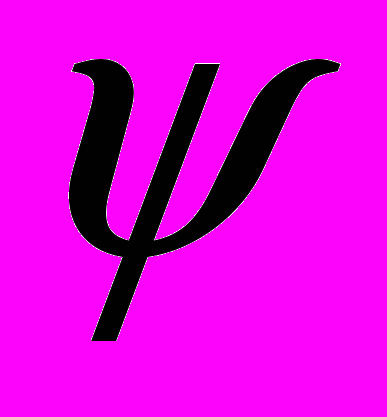- любое положительное число. Это неравенство может быть использовано в теории массового обслуживания при доказательстве того, что среднее время пребывания заявки в системе при взаимопомощи между каналами меньше среднего времени пребывания заявки в системе без взаимопомощи.2. Теория массового обслуживания в экономической сфере. (Учебное пособие. Рекомендательный гриф Министерства общего и профессионального образования РФ).– М.: “Банки и биржи”, Издательское объединение ЮНИТИ, 1998.-320 с. (В соавторстве с Лабскером Л. Г.).
Рассмотрены основы теории массового обслуживания, ее применение в моделировании система массового обслуживания в различных областях экономики, проанализированы простейшие системы, в которых протекает Марковский процесс «гибели и размножения». Представлены тексты разработанных программ, позволяющие использовать при решении задач персональный компьютер. Для студентов, магистрантов и аспирантов, изучающих в вузах курс экономико-математического моделирования.
3. О среднем времени пребывания заявки в системе массового обслуживания//Актуальные проблемы математического моделирования в финансово-экономической области: Сб. научных статей; Финансовая
академия при Правительстве РФ. Кафедра математического моделирования экономических процессов.–М.:ФА,1999.-С.3-10.( В соавторстве с Лабскером Л. Г.).
Дано подробное аналитическое доказательство тому, что среднее время пребывания заявки в многоканальной СМО с отказами и равномерной взаимопомощью между каналами меньше среднего времени пребывания заявки в СМО без взаимопомощи.
4. Основы финансового анализа рынка ценных бумаг (Учебное пособие). — М.: Финансовая академия при Правительстве РФ, 1999. — 120 с. (В соавторстве с Абламской Л. В.).
Изложены основы математических методов и моделей, используемых для количественного анализа рынка ценных бумаг.
5. Прогнозирование финансовых индексов по данным временных рядов (Монография). — М.: Перспектива, 1999 г. — 112 с.
Посвящена моделям финансовой эконометрики. Предложен новый подход к решению задач прогнозирования финансовых индексов, основанный на применении коллокационных методов.
6. Параметрическая модель среднеквадратической коллокации и равновесные модели формирования доходности финансовых активов// Информационный бизнес в России: Сборник научных трудов; Тамбовский гос. техн. ун-т. — Тамбов: ТГТУ,1999.- Вып. II.-С.3-9.
Модель параметрической коллокации рассматривается как обобщение регрессионных моделей, учитывающее помимо тренда и случайного возмущения стохастическую составляющую случайного процесса — сигнальную. В работе показана взаимосвязь параметрической коллокации и равновесных моделей формирования доходностей ценных бумаг.
7. Обзор коллокационных моделей прогнозирования финансовых индексов//Математические и информационные методы исследования экономики: Сборник научных трудов. — М.: Перспектива, 1999.- С. 31-44.
Приводится формулировка и решение задач локальной и глобальной коллокаций применительно к построению прогнозов финансовых индексов. Выполнен сравнительный анализ прогнозов финансовых индексов в рамках моделей чистой и параметрической коллокаций.
8. Сопоставление объясняющих способностей современных моделей стохастического прогнозирования финансовых индексов// Математические и информационные методы исследования экономики: Сборник научных трудов.— М.: Перспектива, 1999.-С.50-60. (В соавторстве с Бывшевым В. А.).
Обсуждается процедура прогноза значений финансовых индексов в рамках модели П. Самуэльсона экономического броуновского движения с дискретным временем и алгоритма прогнозирования уровней финансовых индексов по разнородной информации в рамках стационарной модели “логарифмической прибыли”. Выполнено сопоставление точностных характеристик краткосрочного прогнозирования финансовых индексов РТС, при помощи процедур, обсужденных в этой работе, а также программных модулей, реализованных в системе STATISTICA.
9. О влиянии равномерной взаимопомощи между каналами на среднее время пребывания заявки в многоканальной системе массового обслуживания // XXI век: новая модель специалиста-экономиста: Тезисы докладов на Международной научно-методической конференции (г. Москва, 28-30 марта 2000 г.) / Москва, Финансовая академия при Правительстве РФ.- М.: ФА, 2000.-Часть 5.-С. 143-147. (В соавторстве с Лабскером Л. Г.).
Сформулировано утверждение о том, что равномерная взаимопомощь между каналами в многоканальной СМО с ожиданием и ограничением на длину очереди уменьшает среднее число заявок в очереди, среднее число заявок под обслуживанием и, следовательно, уменьшает среднее время ожидания заявки в очереди и среднее время обслуживания заявки.
10. О влиянии равномерной взаимопомощи между каналами на среднее время пребывания заявки в многоканальной системе массового обслуживания // Качество информационных услуг: Сб. научных трудов; Министерство образования РФ, Финансовая академия при Правительстве РФ, Московский гос. ун-т коммерции, Тамбовский гос. техн. ун-т.-Тамбов: ТГТУ, 2000.-Вып. III.-С. 43-52. (В соавторстве с Лабскером Л. Г.).
Дано развернутое изложение вместе с доказательствами результатов, анонсированных в тезисах под номером 9 в настоящем списке.
11. Об одном неравенстве и его использовании в теории массового обслуживания // Актуальные проблемы математического моделирования в финансово-экономической области; Сб. научных статей; Финансовая академия при Правительстве РФ. – М.: ФА, 2000.-С.3-15. (В соавторстве с Лабскером Л. Г.).
Дано подробное доказательство справедливости неравенства, анонсированного в тезисах под номером 1 в настоящем списке.
12. Регрессионные модели финансового анализа (Учебное пособие. Гриф УМО). — М.: Финансовая академия при Правительстве РФ, 2000 г. — 124 с.
Рассмотрены вопросы построения классических регрессионных моделей и некоторые их обобщения, связанные с преодолением нарушений предпосылок Гаусса-Маркова.
13. Коллокационная модель прогнозирования количественных характеристик основных финансовых инструментов фондового рынка // Вестник Финансовой Академии.-2000.-№ 2.-С.77-86.
Излагается алгоритм средней квадратической коллокации, используемый для построения оптимальных прогнозов инструментов фондового рынка.
14. Выбор ковариационных функций в коллокационных моделях прогнозирования // Модели экономических систем и информационные технологии: Сборник научных трудов; Финансовая академия при Правительстве РФ.-М.: ФА, 2000.- Вып. II.-С.8-15.
Обсуждаются модели ковариационных функций и методы оценки их параметров по выборочным данным.
15. Сравнительный анализ прогнозов финансовых индексов в рамках моделей экономического броуновского движения и авторегрессии проинтегрированного скользящего среднего // Модели экономических систем и информационные технологии: Сборник научных трудов.—М.: Перспектива, 2000.- Выпуск III.- С.16 -22.
В работе получена формула для оценки "логарифмической прибыли" за определенный период упреждения в рамках модели ЭБД и выполнен сравнительный анализ прогнозов индекса РТС по моделям ЭБД и АРПСС.
16. Модели прогнозирования финансовых индексов по данным временного ряда//Вестник Финансовой Академии/ —М.: 2000.- № 4. С.55-65.
Выполнено прогнозирование значений индекса РТС в рамках модели АРПСС в программном модуле системы STATISTICA и коллокационных моделей. Приводится сравнительный анализ прогнозов.
17. Алгоритм оценивания основных инвестиционных характеристик финансовых активов при помощи оптимальной статистической процедуры Эйткена // Управление риском. —М.: 2000.- № 4.- С.31 -37. (В соавторстве с Бывшевым В. А. и Арсеньевой Л. В.).
Обсуждается применение процедуры МНК Эйткена для оценки основных числовых характеристик вектора доходности финансового инструмента. Выполнено оценивание инвестиционных характеристик казначейских векселей США при помощи процедуры Эйткена.
18. Алгоритм оценивания основных инвестиционных характеристик финансовых активов при помощи оптимальной статистической процедуры Эйткена//XXI век: новая модель специалиста – экономиста: Тезисы докладов и выступлений на Международной научно-методической конференции —М.: ФА, 2000.- Ч. 5.- С.130-131. (В соавторстве с Бывшевым В. А. и Арсеньевой Л. В.).
Обсуждается применение процедуры МНК Эйткена для оценки основных числовых характеристик вектора доходности финансового инструмента. Выполнено оценивание инвестиционных характеристик казначейских векселей США при помощи процедуры Эйткена.
19. Параметрическая модель среднеквадратической коллокации и модель оценки капитальных активов//XXI век: новая модель специалиста – экономиста: Тезисы докладов и выступлений на Международной научно-методической конференции.- М.: ФА, 2000.- Ч. 5.—С.127-129.
Модель параметрической коллокации рассматривается как обобщение регрессионных моделей, учитывающее помимо тренда и случайного возмущения стохастическую составляющую случайного процесса — сигнальную. В работе показана взаимосвязь параметрической коллокации и равновесных моделей формирования доходностей ценных бумаг.
20. Краткий обзор стохастических моделей прогнозирования характеристик фондового рынка//Актуальные проблемы математического моделирования в финансово-экономической области: Сборник научных статей.-М.: ФА, 2000.- Вып. 2.-С. 81-89.
В статье рассматриваются математические модели фондового рынка, составляющие (начиная с 50-х годов) основу инструментария управления инвестициями.
21. Коллокационные модели прогнозирования и их применение в финансовой сфере (Монография).- М.: Экзамен, 2001 г. — 288 с.
Изложены функциональный и статистический подходы построения коллокационных моделей. Приводятся алгоритмы прогнозирования финансовых индексов и оценки точности прогнозов в рамках моделей средней квадратической и параметрической коллокаций.
22. Игровые методы в управлении экономикой и бизнесом (Учебное пособие. Гриф УМО). — М.: ДЕЛО, 2001. — 464 с. (В соавторстве с Лабскером Л. Г.).
В пособии излагаются основы теории игр, охватывающие вопросы принятия оптимальных решений в условиях антагонистической конкуренции, риска и неопределенности.
23. Связь оценок параметрической коллокации с решением некорректно поставленных задач//Актуальные проблемы математического моделирования в финансово-экономической области: Сборник научных трудов; Финансовая академия при Правительстве РФ. — М.: ФА, Вып. 3.- 2001.- С. 4-13.
Приводится вывод основных уравнений параметрической коллокации, основанный на использовании стандартной техники вариационного исчисления в гильбертовом пространстве.
24. Алгоритм прогнозирования финансовых индексов в рамках стационарной модели Колмогорова-Винера. // Финансовая математика. — М.: ТЕИС, 2001.-С.156-165. (В соавторстве с Бывшевым В. А.).
Построен алгоритм, комбинирующий процедуры оптимального несмещенного оценивания математического ожидания логарифмической прибыли и оптимального прогноза Колмогорова- Винера.
25. Прогнозирование финансовых показателей и концепции финансовых рынков//Модели экономических систем и информационные технологии: Сб. научных трудов. —М.: ФА, 2001.-Вып. IV.-С. 8 - 15.
В работе рассмотрена взаимосвязь стохастических моделей описания динамики финансовых индексов и концепций финансовых рынков, положенных в их основу.
26. Коллокационные модели прогнозирования доходности ценных бумаг// Монография "Финансовая математика". —М.: ТЕИС, 2001.-С.105-115.
Приводится вывод основных формул алгоритма параметрической коллокации в рамках обобщенного принципа наименьших квадратов, критерий оптимальности которого включает блочный вектор, частями которого являются вектор возмущений и вектор сигналов.
27. Прогнозирование финансовых индексов в рамках стационарных моделей "логарифмической прибыли”// Качество информационных услуг: Сборник научных трудов.— Тамбов.:ТГТУ, 2001 г.,— Вып. IV.- Т. 2.- С. 19 -34. (В соавторстве с Бывшевым В. А.).
Выполнено обобщение алгоритма прогнозирования финансовых индексов в рамках стационарной модели логарифмической прибыли на случай разнородной информации.
28. Прогнозирование финансовых индексов в рамках стационарных моделей "логарифмической прибыли”//Современные образовательные технологии подготовки специалистов-экономистов в вузах России: Тезисы докладов и выступлений на Международной научно-методической конференции (г. Москва, 27-30 марта 2001 г.)/ Финансовая академия при Правительстве РФ. —М.: ФА, 2001.- Ч. 4.-С.126-129.
Приведен результат сравнения прогнозной способности коллокационных моделей при использовании однородной и разнородной информации.
29. Алгоритм прогнозирования финансовых индексов в рамках модели экономического броуновского движения// Модели экономических систем и информационные технологии: Сборник научных трудов; Финансовая академия при Правительстве РФ.-М.-ФА, 2002.- Выпуск VI.-С.75-85. (В соавторстве с Бывшевым В. А.).
Обсуждаемый в статье рандомизированный алгоритм предусматривает возможность оптимального (в среднем квадратическом) прогноза в рамках модели Самуэльсона экономического броуновского движения (со сносом).
30. Экономико-математическое моделирование (Учебник. Гриф УМО) Главы 2,6./ Под общ. ред. И. Н. Дрогобыцкого.- М.: ЭКЗАМЕН, 2004.- 800 с.
Детально проанализированы: основы теории игр, методы математического программирования в построении и анализе экономико-математических моделей. Особое место занимают Марковские процессы и элементы теории массового обслуживания, моделирование производственных процессов и сферы потребления.
31. Прогнозирование динамических рядов финансово-экономической информации рандомизированным алгоритмом коллокации//Управление риском. — М.: 2004.-№ 1.-С. 35-39. (В соавторстве с Бывшевым В. А. и Клапко А. О.).
Обсуждается рандомизированный алгоритм стохастического прогнозирования финансовых индексов, в рамках стационарной модели логарифмической прибыли.
32. Эквивалентность двух алгоритмов оценивания параметров системы одновременных уравнений двухшаговым методом наименьших квадратов // Математические и инструментальные методы экономического анализа: управление качеством: Сборник научных трудов; Тамбовский техн. гос. ун-т.—Тамбов: ТГТУ, 2004.- Выпуск 12.- С. 142-153.
Показана взаимосвязь: оценок параметров структурной формы СОУ двухшаговым методом наименьших квадратов (ДМНК) и оценок, полученных в рамках метода инструментальных переменных; оценок ДМНК и оценок второго шага трехшагового метода (ТМНК).
33. Уточнение рисковой надбавки тарифной ставки в рисковых видах страхования// Вестник Финансовой Академии. — 2004-№ 4-С.40-47. (В соавторстве с Груздевой Л. В.).
Выполнен сравнительный анализ значений тарифных ставок в рисковых видах страхования, оцененных в рамках эконометрической модели и методики, рекомендованной Федеральной службой России по надзору за страховой деятельностью.
34. Сравнительный анализ методов проверки гипотезы стационарности динамического ряда значений “логарифмической прибыли”// Актуальные проблемы математического моделирования в финансово-экономической области: Сборник научных статей. - М.: Финансовая академия при Правительстве РФ, Кафедра Математического моделирования экономических процессов.- 2004.- Вып. 6. С. 4-13 (В соавторстве с Клапко А. О.).
Получены формулы для вычисления оценок математического ожидания и дисперсии показателей обнаружения тенденции изменения основных характеристик уровней ряда в рамках метода Фостера-Стюарта. Выполнен сравнительный анализ методов разности средних уровней ряда и Фостера-Стюарта, как наиболее простых в практической реализации.
35. Основы эконометрического моделирования (Учебное пособие. Гриф УМО).— М.: КомКнига, 2006.— 432 с.
Приводится подробное описание этапов построения эконометрических моделей, принципов составления спецификации, алгоритмов оценки параметров и проверки адекватности. Рассматриваются вопросы оценки параметров систем одновременных уравнений и анализа временных рядов. Первое место по номинации "Учебное пособие" в ежегодном конкурсе на лучшие учебно-научные издания в 2006 году в ФГОУ ВПО «Финансовая академия при Правительстве Российской Федерации», приказ №57-1/0 от 19.03.07 г.
36. Проверка адекватности прогнозов финансовых индексов в рамках модели рандомизированной коллокации//Актуальные проблемы математического моделирования в финансово-экономической области: Сборник научных статей; Финансовая академия при Правительстве РФ, Кафедра математического моделирования экономических процессов.-М.:ФА,2006.- Выпуск 6.-С.27-35. (В соавторстве с Бывшевым В. А. и Клапко А. О.).
Получены формулы для вычисления границ доверительных интервалов для каждой ветви рандомизированного алгоритма прогнозирования финансовых индексов. Выполнена проверка адекватности рандомизированной модели коллокации.
37. Проверка адекватности рандомизированной модели коллокации // Экономическое прогнозирование: модели и методы: Материалы IV Международной научно-практической конференции (г. Воронеж, 10-11 апреля 2008 г.)/ Воронежский гос. ун-т. - Воронеж: Издательско-полиграфический центр ВГУ.-2008.- Ч.2.—С. 30-33. (Совместно с Бывшевым В. А.).
Обсуждается рандомизированный алгоритм точечного и интервального прогнозирования финансовых индексов в рамках коллокационных моделей. Выполнена проверка адекватности рандомизированной модели коллокации.
38. Математическое моделирование финансовой деятельности (Учебное пособие. Гриф УМО).— М.: Финансовая академия при Правительстве РФ, 2008. — 226 с.
Содержит вопросы моделирования динамики внешнего долга, экономические приложения моделей финансовой эконометрики.
39. Оценка точности прогноза резерва позднего убытка в Excel// Электронный бизнес: проблемы, развитие и перспективы: VII Всероссийская заочная научно-практическая конференция (г. Воронеж, 4-5 декабря 2008 г.).-Воронеж: 2008.- С. 6-11.
Формула для оценки точности резерва позднего убытка выражена через статистики, приведенные в функции ЛИНЕЙН табличного процессора Excel.
Бакушева Галина Вячеславовна
1. Потребности вузов как стимул развития социальной инфраструктуры // Университеты как центры развития региона: Материалы II Российско-Американской региональной конференции (г. Йошкар-Ола, 9-11 декабря 1999 г.). - Йошкар-Ола: МарГУ, 1999.-С.170-171 (в соавторстве с Паймаковой Г. А.).
Дается краткое описание основных элементов инфраструктуры сферы образования Республики Марий Эл. Система образования в ряду социальных проблем региона играет особенно важную роль.
2. Обучающие Internet - технологии глазами студента // Диалог науки и практики в поисках новой парадигмы общественного развития России в новом тысячелетии: Всероссийская постоянно действующая научная конференция. Четвертые Вавиловские чтения. - Йошкар-Ола, 2000.- Ч. 2.-С. 109-110.
Рассматриваются достоинства Internet-лекций с точки зрения студента: легкий поиск нужной информации, доступность данных в любой момент времени для любого количества пользователей, возможность дополнения актуальной информацией и т.д.
3. Информационные ресурсы как фактор экономических противоречий // Актуальные проблемы современной науки: Тезисы докладов 2-й Международной конференции молодых ученых и студентов (г. Самара, 11-13 сентября 2001 г.). – Самара: СамГУ, 2001.- Ч. 6.- С.97 (в соавторстве с Царегородцевым Е. И.).
Ставится вопрос о признании информации фактором экономического и социального развития. Один из аргументов: низкий уровень образования – это меньшие возможности использования достижений информационной технологии.
4. Возникновение анимистических представлений о сущности жизни // Материалы 54-й межвузовской студенческой научно-технической конференции (Йошкар-Ола, 16-26 апреля 2001г.). – Йошкар-Ола: МарГТУ, 2001.-С. 142-143 (в соавторстве с Маслихиным А. В.).
Кратко описывается возникновение и развитие анимистических представлений о сущности жизни, которые менялись в ходе истории в зависимости от общего процесса развития культуры и связанного с ним накопления человеческих знаний.
5. Инвестиционный климат в России // Мировое сообщество и Россия на путях модернизации. Экономика и управление в современном обществе: Всероссийская постоянно действующая научная конференция. Пятые Вавиловские чтения. - Йошкар-Ола: МарГТУ, 2002 г.- С.29-34 (в соавторстве с Паймаковой Г.А.).
Рассматривается картина инвестиционного климата России, а также затрагиваются проблемы инвестиционного климата конкретного региона: Республики Марий Эл.