Магистерская программа «Государственные и муниципальные финансы» Кафедра государственного управления и экономики общественного сектора магистерская диссертация

Вид материала

Программа

Содержание 2.3 Анализ факторов, влияющих на занятость на рынке труда врачей. Таблица 3. Уравнение зависимости численности врачей на 10000 человек от относительной заработной платы врачей и ВРП на душу насе Таблица 9. Тест Бройша-Пагана на выбор спецификации модели со сквозной регрессией и модели Random Effect. Таблица 10. Тест Хаусмана на выбор спецификации модели Fixed Effect и Random Effect.

Подобный материал:

• Магистерская программа «Государственные и муниципальные финансы» Кафедра государственного, 867.91kb.
• Программа дисциплины ''Полюса и зоны роста мировой экономики'' для направления 080100., 62.74kb.
• Рабочая программа по дисциплине Государственный кредит и госдолг 06. 04 «Финансы, 389.27kb.
• Магистерская программа Прикладная экономика Кафедра магистерская диссертация роль лизинга, 822.73kb.
• Программа дисциплины информационные системы в экономике и финансах для направления, 208.51kb.
• Программа дисциплины внутренний аудит для направления 080100. 68 «Экономика» подготовки, 319.46kb.
• М. В. Ломоносова Экономический факультет Кафедра «Финансы и кредит» Магистерская диссертация, 895.77kb.
• Программа дисциплины «Экономика общественного сектора» для направления 030900. 68 «Юриспруденция», 213.46kb.
• Методические указания к выполнению контрольной работы. Дисциплина «Государственные, 31.96kb.
• Программа дисциплины внешний аудит и консалтинг для подготовки магистров по направлению, 384.13kb.

2.3 Анализ факторов, влияющих на занятость на рынке труда врачей.

В итоге, учитывая все ограничения данных, описанные выше, была получена выборка, состоящая из 327 наблюдений.

Попытаемся выявить, от каких факторов может зависеть заработная плата врачей в регионе. То есть оценим уравнение регрессии, имеющее следующий общий вид:


Qvrach_i = α + β₁ ozpvr_i + β₂ vrp_i + β₃ bezrabotica_i +ε_i. (2.1)


где qvrach – количество врачей на 10000 человек населения;

ozpvr – относительная заработная плата врачей;

vrp – натуральный логарифм ВРП на душу населения;

bezrabotica – уровень безработицы;

ε – ошибка в модели;

i – индивидуальный идентификатор (регион).


Прежде чем провести сквозное оценивание уравнения нашей модели, игнорирующее панельную природу данных, воспользуемся пошаговой процедурой исключения переменных (табл. 2):


Таблица 2. Процедура исключения переменных в модели зависимости численности врачей на 10000 человек от относительной заработной платы врачей, уровня безработицы и валового регионального продукта на душу населения.



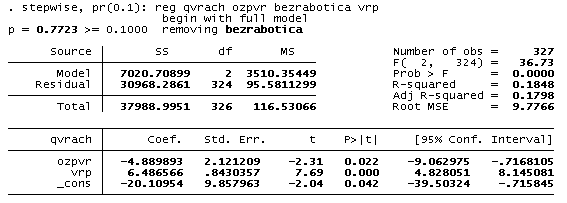
Как видно из таблицы 2, коэффициенты при всех факторах за исключением безработицы значимы на 5% уровне, поэтому все они могут являться объясняющими для данной модели.

Построим сквозную регрессию, исключив из рассмотрения переменную безработицы как незначимый фактор (табл. 3).


Таблица 3. Уравнение зависимости численности врачей на 10000 человек от относительной заработной платы врачей и ВРП на душу населения.



Значения коэффициентов детерминации (R-squared и Adj R-squared) невелико, что типично для такого рода данных и, скорее всего, зависимость может объясняться наличием каких-либо других значимых факторов, которые не были учтены в модели. Однако F-тест показывает значимость зависимости в целом. Все переменные значимы на 5% уровне. Причем число врачей в регионе (qvrach) отрицательно зависит от уровня относительной заработной платы (ozpvr) и положительно от уровня ВРП (lnvrp).

Построим эту же модель без константы (табл. 4).


Таблица 4. Уравнение зависимости численности врачей на 10000 человек от относительной заработной платы врачей и ВРП на душу населения, без константы.



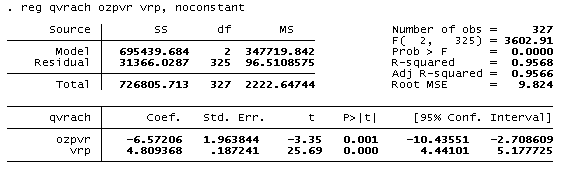
Как видно из таблицы 4, значения коэффициентов несколько снизились. Но в этом случае мы получили неитерпретируемый R-квадрат, потому имеет смысл остановиться на предыдущей спецификации.

Прокомментируем особенности, связанные с оцениванием этой модели. В исследуемой нами панели участвует 327 наблюдений, но не для всех из них оказывается доступной вся запрашиваемая информация. Если в каком-то году результат наблюдения по одному из регионов отсутствует, программа игнорирует все наблюдения, по региону, относящиеся к этому году, поэтому в среднем регионы наблюдаются не 6 лет, а 5.7 года.

Нужно отметить, что, оценивая последние регрессии, мы исходили из предположения о некоррелированности индивидуального эффекта и независимых переменных, но это предположение не вполне обосновано. В ненаблюдаемый индивидуальный эффект входят различные компоненты, например, наличие в регионе крупных городов и предприятий, которые, как правило, коррелируют с уровнем его развития, валовым продуктом. Из сказанного следует, что модель с детерминированным индивидуальным эффектом (Fixed effect - FE) может быть более адекватна данным. Оценим теперь ее (табл. 5):


Qvrach_it = α + β₁ ozpvr_it + β₂ vrp_it + β₃ bezrabotica_it +ε_it. (2.2)


где qvrach – количество врачей на 10000 человек населения;

ozpvr – относительная заработная плата врачей;

vrp – натуральный логарифм ВРП на душу населения;

bezrabotica – уровень безработицы;

ε – ошибка в модели;

i – индивидуальный идентификатор (регион);

t – временной идентификатор (год).


Таблица 5. Уравнение зависимости численности врачей на 10000 человек от относительной заработной платы врачей, уровня безработицы и ВРП на душу населения, в модели Fixed Effect.



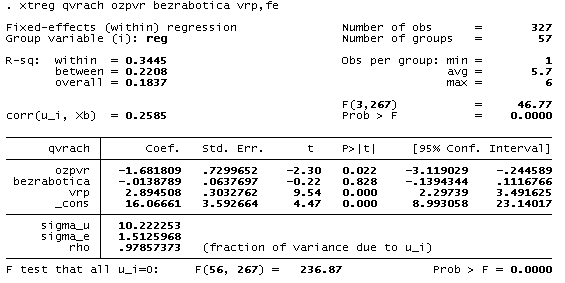
Модель значима по F-тесту. Коэффициенты, за исключением безработицы (bezrabotica) значимы по t-тесту. Исключим из рассмотрения незначимый фактор безработицы и построим новую регрессию (табл. 6):


Таблица 6. Уравнение зависимости численности врачей на 10000 человек от относительной заработной платы врачей и ВРП на душу населения, в модели Fixed Effect.



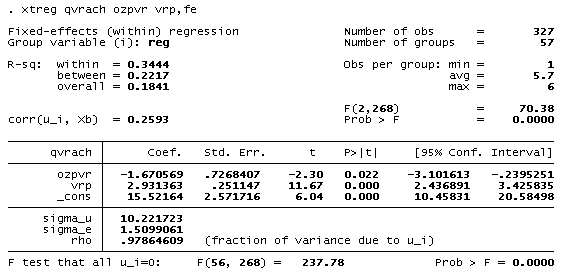
О качестве подгонки в этой модели следует судить по коэффициенту детерминации 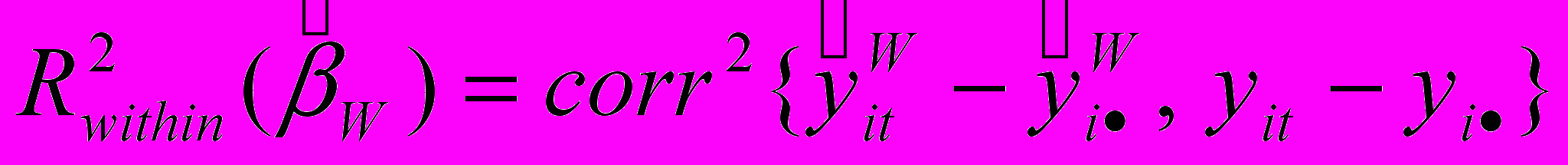=34,44%, который оказывается значительно выше, чем для сквозной регрессии. Большая часть вариации данных (98%) приходится на индивидуальные эффекты: rho = 0.9786. «Объединенная модель» против альтернативы «модели FE» проверяется F-тестом. Таким образом, гипотеза о равенстве нулю всех индивидуальных эффектов отвергается на 1% уровне значимости: модель FE предпочтительнее объединенной модели.

Теперь проверим модель со случайными индивидуальными эффектами (Random Effect – RE) (табл. 7).


Таблица 7. Уравнение зависимости численности врачей на 10000 человек от относительной заработной платы врачей, уровня безработицы и ВРП на душу населения, в модели Random Effect.



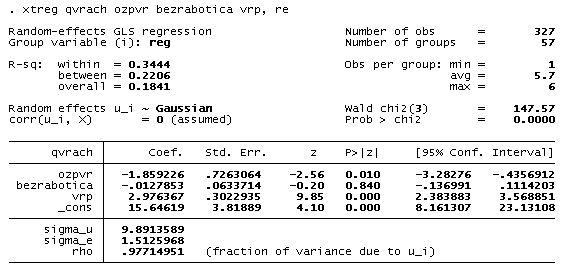
Фактор безработицы, как и в предыдущих спецификациях, является незначимым. Поэтому имеет смысл построить регрессию без него (табл. 8).


Таблица 8. Уравнение зависимости численности врачей на 10000 человек от относительной заработной платы врачей и ВРП на душу населения, в модели Random Effect.



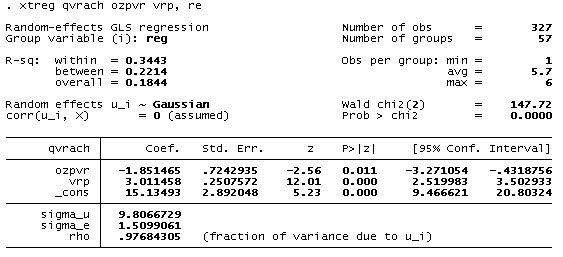
Для осуществления выбора между сквозной регрессией и регрессией со случайным индивидуальным эффектом проделаем тест Бройша-Пагана (табл. 9):


Таблица 9. Тест Бройша-Пагана на выбор спецификации модели со сквозной регрессией и модели Random Effect.



Таким образом, гипотеза о равенстве 0 дисперсии индивидуального эффекта может быть отвергнута на 1% уровне значимости: модель со случайным индивидуальным эффектом (Таблица 8) предпочтительнее объединенной модели (Таблица 3).

И, наконец, с помощью теста Хаусмана проверим, какая из моделей, со случайными или с детерминированными индивидуальными эффектами (таблица 8 и таблица 6) более предпочтительна:


Таблица 10. Тест Хаусмана на выбор спецификации модели Fixed Effect и Random Effect.



По результатам теста, гипотеза о состоятельности оценок модели Random Effect отвергается в пользу альтернативной гипотезы о состоятельности оценок модели Fixed Effect.

Поскольку наиболее предпочтительной является модель с детерминированным индивидуальным эффектом (FE), итоговое уравнение имеет вид (Таблица 6):


Qvrach_it = 15.522 – 1.671 ozpvr_it + 2.931 lnvrp_it + ε_it. (2.3)