Гармонический сигнал основная форма токов в электросиловых цепях. Метод комплексных амплитуд линеаризация уравнений при условии линейности аналогов

Вид материала

Лекция

Содержание То есть в линейных системах гармонический сигнал не порождает новые частоты Z называют импедансом

Подобный материал:

• Лекция 1, 259.64kb.
• Лекция 3, 169.64kb.
• Задание: Составить систему уравнений по законам Кирхгофа для расчета токов ветвей., 17.99kb.
• Календарный план учебных занятий по дисциплине «Математическое моделирование». Лектор, 35.95kb.
• Урок физика-математика «Расчет комплексных сопротивлений в электрических цепях переменного, 117.95kb.
• Методические рекомендации по подготовке к сдаче государственного экзамена Раздел «Математика», 38.2kb.
• Практических: 0 Лабораторных:, 21.53kb.
• Решение. Из анализа схемы следует, что резисторы, 80.22kb.
• Решение. Метод контурных токов, 63.32kb.
• Лекция № Расчет переходных процессов в линейных цепях. Операторный метод. Некоторые, 48.92kb.

Лекция 2. Гармонический сигнал - основная форма токов в электросиловых цепях. Метод комплексных амплитуд – линеаризация уравнений при условии линейности аналогов. Потенциальные и векторные диаграммы. Активная, реактивная и полная мощность. Простые RC- RL-цепи. Электрический резонанс напряжений и токов. Вторичные параметры.


Как уже известно, электрохимические, а также прямого преобразования, источники электропитания обеспечивают потребителя постоянной мощностью. В этом случае реактивная мощность отсутствует, т.е.нет необходимости в применении линейных аналоговых элементов L и С. В схемах замещения при расчётах в режиме постоянного тока они заменяются, соответственно, проводником и разрывом. Это серьёзно упрощает систему уравнений – она становится алгебраической и меньшего порядка. Так как при постоянном токе остаётся только активная мощность, то в основном это приближение применяется для оценки активных потерь или нагрева системы. В отдельных случаях эти источники применяются для получения постоянных электрических и магнитных полей, но здесь просто переходят от напряжений и токов к напряженностям полей Е и Н. Для электростатического поля используют соотношения E=-grad U или q=СU, а для магнитного поля это закон Ампера или полного тока  I=Hdl.

Другой тип источников электропитания - это электромеханические генераторы, которые в основной своей массе основаны на вращении рамки с током в магнитном поле. Магнитный поток, пронизывающий рамку, и, как следует из закона Фарадея или электромагнитной индукции, э.д.с на выходных клеммах, изменяются по гармонической функции е^j(t+) = cos (t+) + jsin (t+) .

Здесь j = -1, мнимая единица, а числа, изображаемые с её помощью – комплексные числа.  - начальный фазовый угол.

Фаза - это событие, которое повторяется с одинаковым временным смещением в каждом периоде гармонических колебаний относительно его начала. Например, ежегодно празднуемый в один и тот же день Ваш день рождения.

Вся прелесть этой функции в том, что она не боится действия интегральных и дифференциальных операторов в том плане, что её зависимость от времени при этом не меняется.

Если U=U_m е^j(t+) , то обобщённый закон Ома для линейных элементов перепишется

I = U/ R = Y U е^j(t+) или I R = U е^j(t+)

I= С dU/dt= jС U е^j(t+) или I/ jС = U е^j(t+) или I/С = U е^j/2

I =1/ L U dt= U_m е^j(t+)/ j L или I j L = U_m е^j(t+) или I L = U е^j/2

Но тогда значит и ток должен меняться по такому же гармоническому закону и с той же частотой , только на реактивных элементах между током и напряжением появляется разность фаз /2. Если бы это было не так, то в какой-то момент времени у нас нарушились бы законы сохранения энергии и заряда (правила Кирхгофа).

То есть в линейных системах гармонический сигнал не порождает новые частоты.

Это очень хорошо для передачи силовой энергии, но плохо для систем передачи информации. И если также учесть, что для систем передачи информации мощность электрического сигнала должна быть минимальной (он служит носителем информации), а в силовых цепях максимальной, то здесь из электротехники начинают выделяться её силовая часть и электроника. Это принципиально разные подходы к созданию электрических устройств. В силовой электротехнике идёт борьба за максимум передаваемой энергии при минимуме частот (все гармоники основной частоты считаются паразитами и с ними идёт жестокая борьба). А в электронике идёт борьба за минимум передаваемой энергии при максимальной ширине области передаваемых частот (в пределе прямоугольный импульс как носитель бита информации).

Изменение тока и напряжения в системах с линейными элементами по гармоническому закону с одной частотой позволяет упростить систему уравнений. Сократив все члены уравнений на временную функцию е^jt , мы просто переведём её из интегральной в алгебраическую формы. Как бы сделаем моментальную фотографию распределения токов и напряжений в системе. Расплатой будет являться переход от действительных чисел, отображаемых на числовой действительной оси х, в область комплексных чисел, отображаемых на плоскости с осями координат (х, j).

В этом случае соотношения обобщенного закона Ома будут выражены как

U_m е^j = R I_m е^j

I_m е^j = jС U_m е^j=( j/Х_C ) U_m е^j U_m е^j=- jХ_C  I_m е^j

U_m е^j = j L  I_m е^j= jХ_L  I_m е^j

Если обозначить комплексные числа 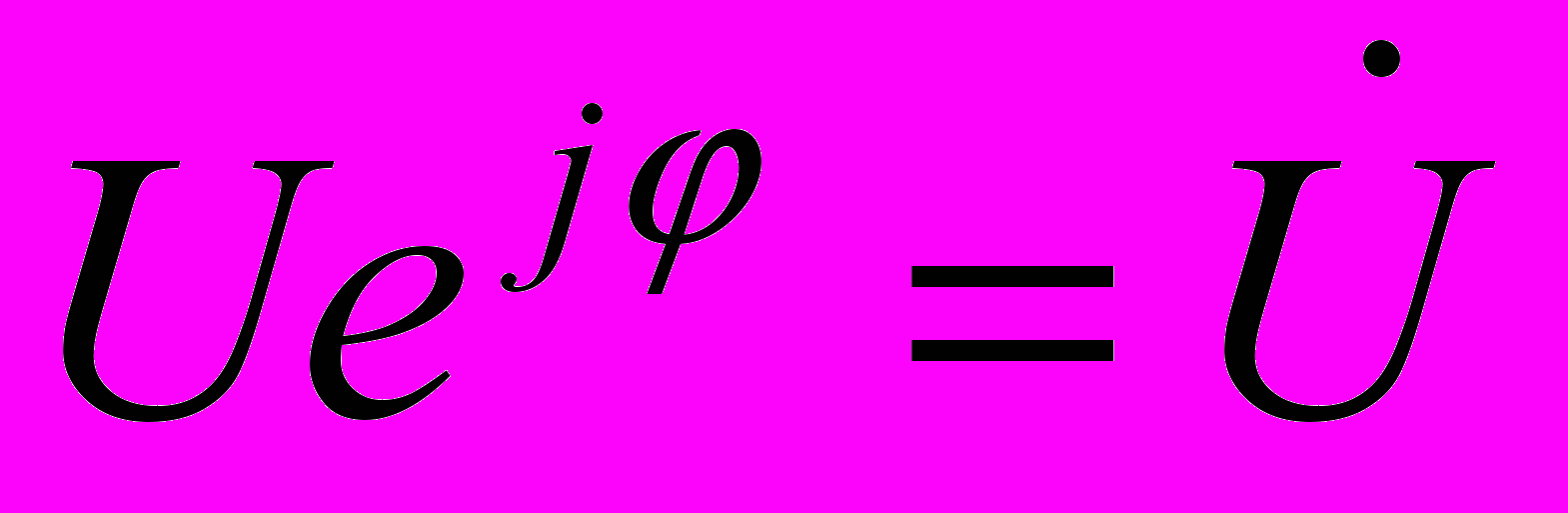и 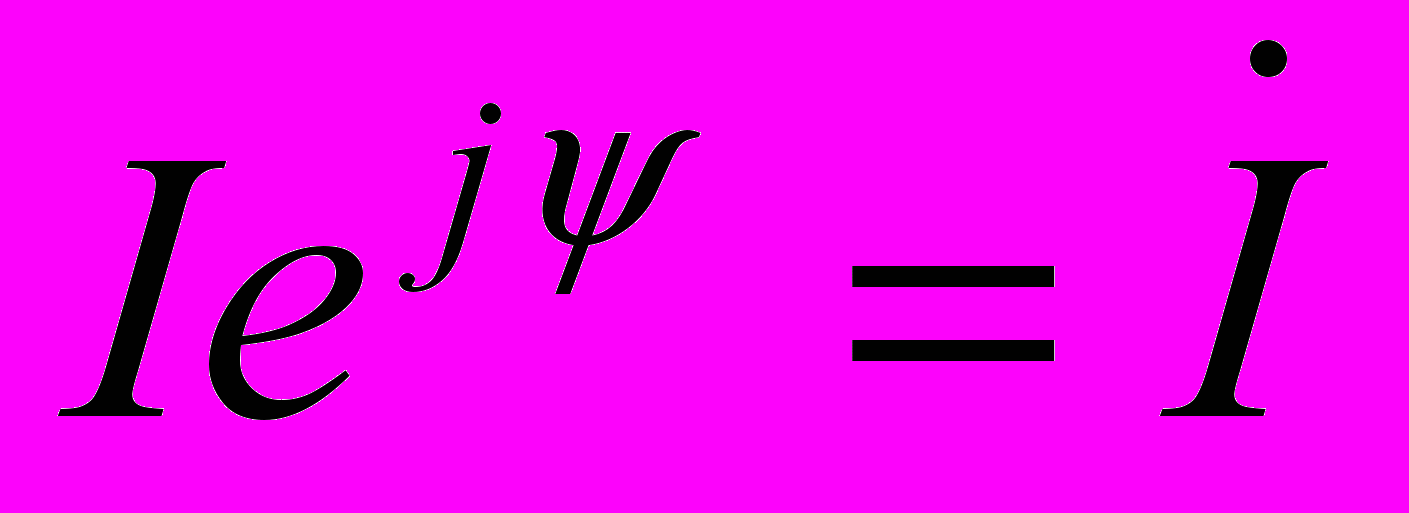, то получим обобщенный закон Ома в виде 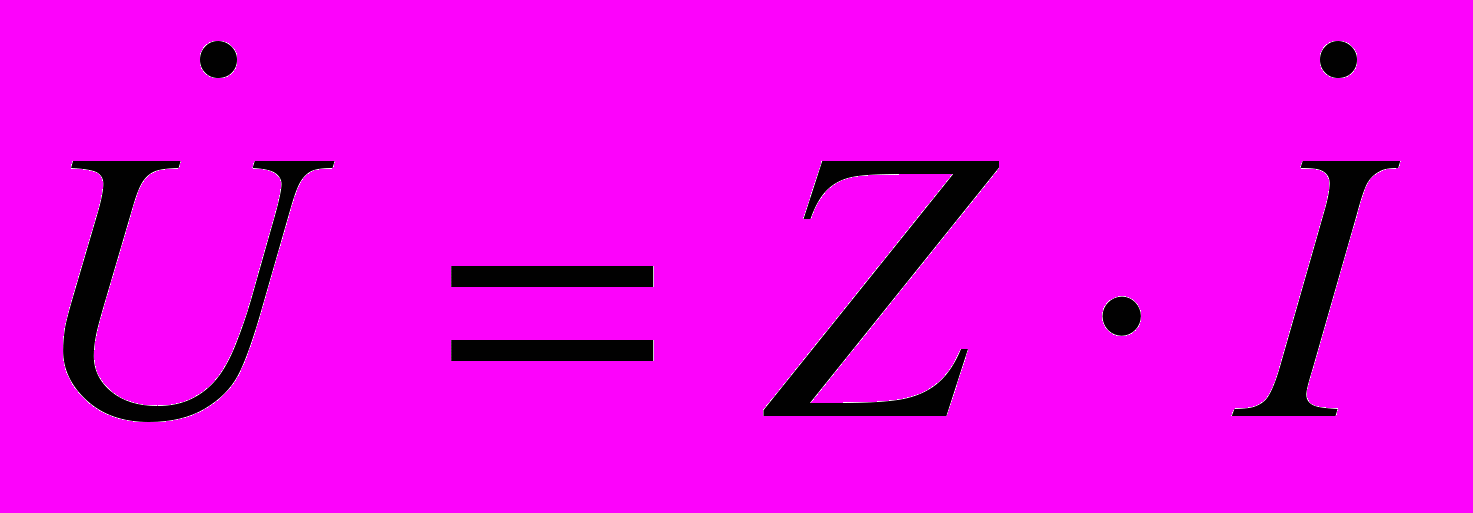. Для отдельных элементов он будет выглядеть следующим образом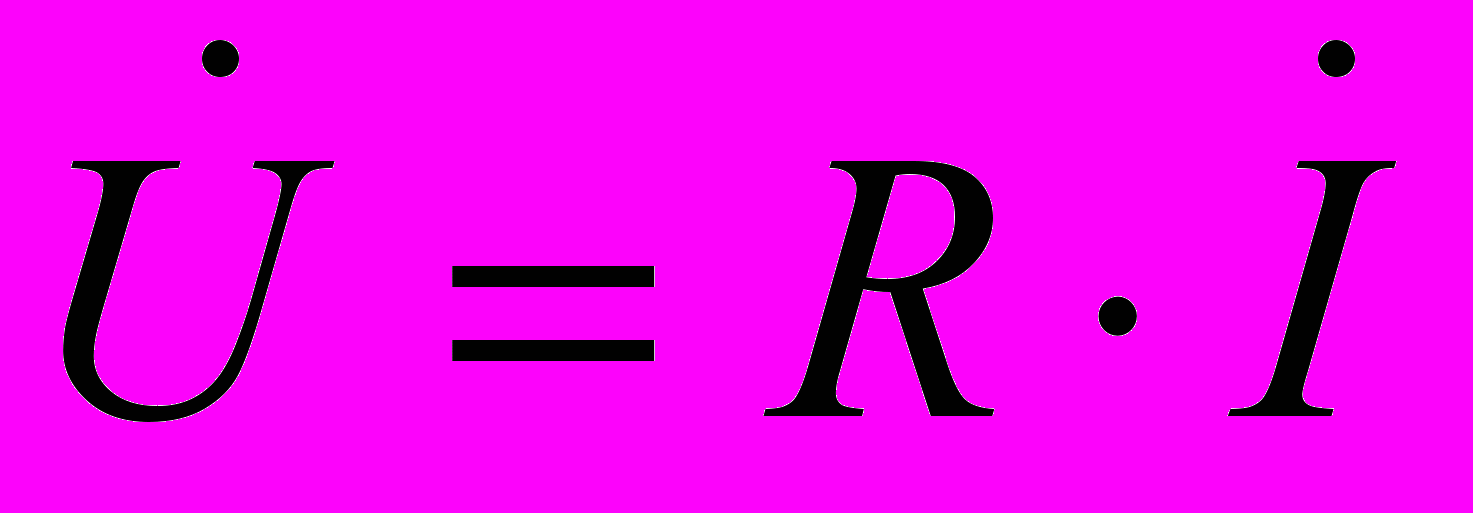







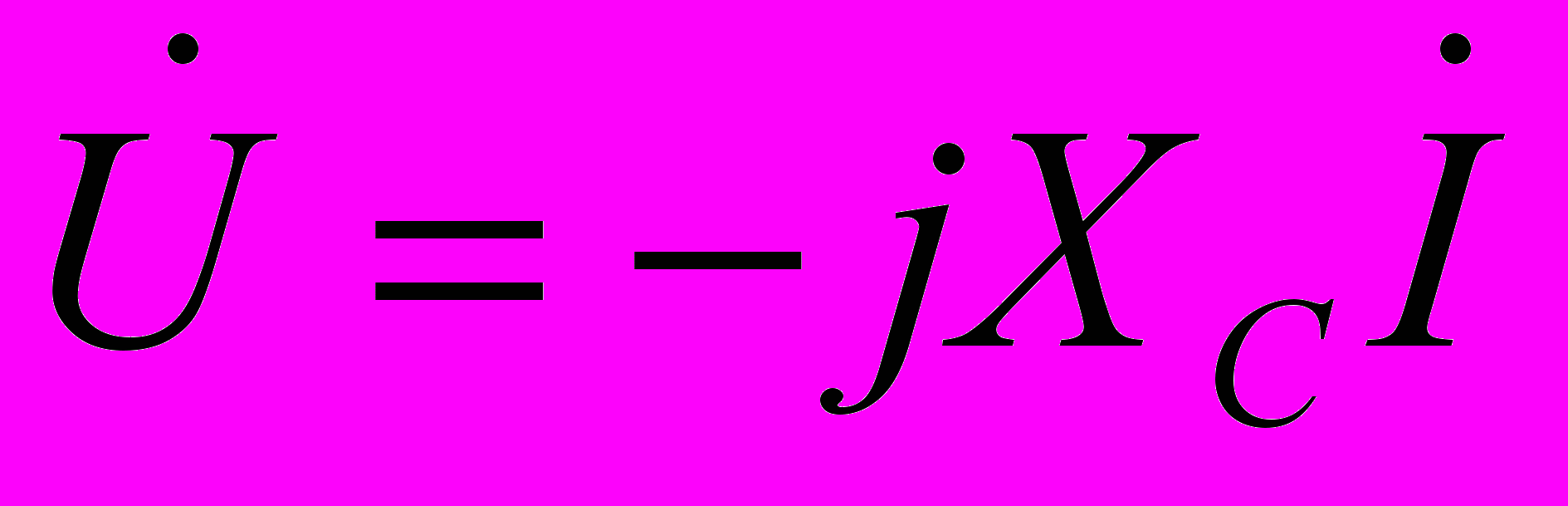
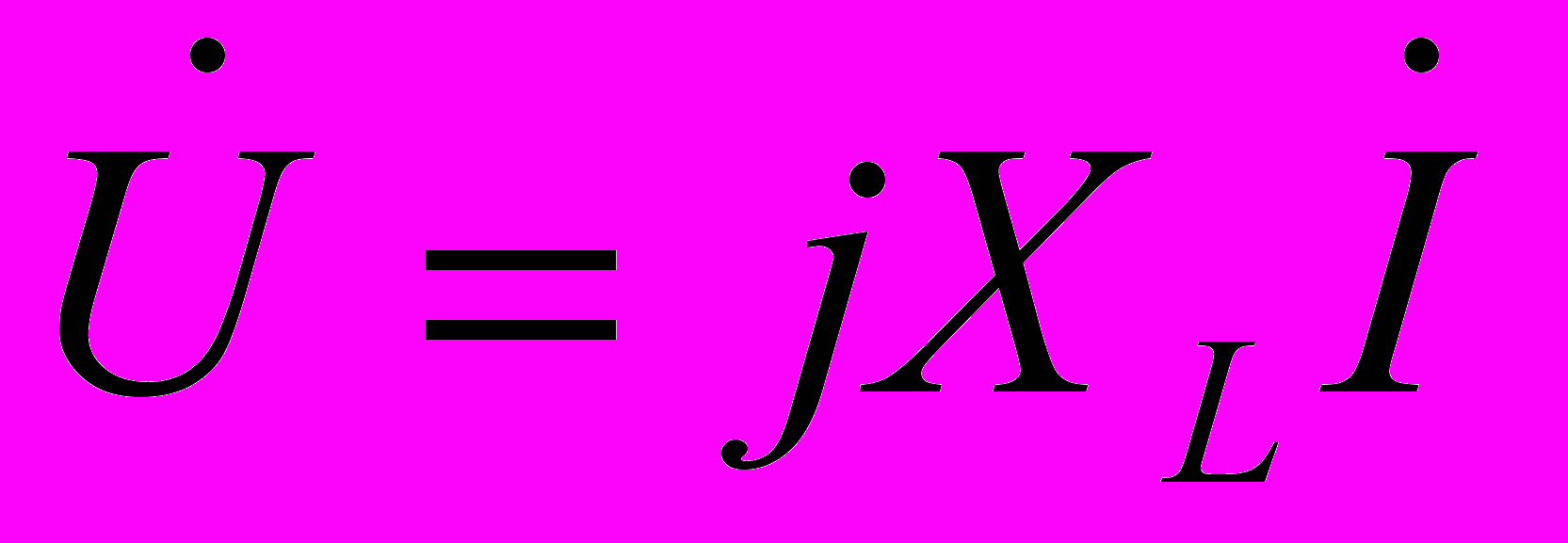
Значения 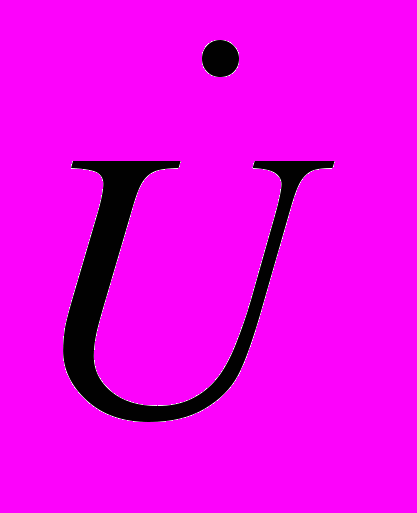и 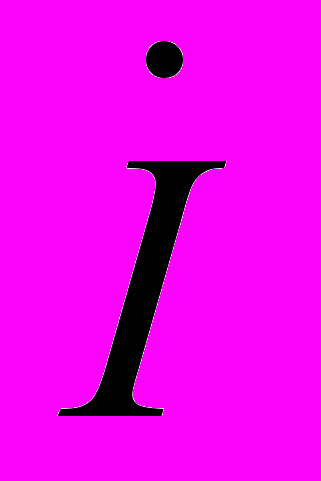получили название комплексов. Эти комплексные числа содержат значение числа и фазовый угол.

На комплексной плоскости они изображаются отрезком прямой с длиной, равной значению параметра, и который расположен под углом равным .

Величину Z называют импедансом или полным сопротивлением, а величины Х_C =1/ωС

и Х_L =ωL называют реактансами участков цепи.

Ясно, что при последовательном соединении всех трёх аналоговых элементов Z=R+j(X_LX_C). То есть мы можем достаточно просто составлять и разрешать алгебраические уравнения, как это делали бы в приближении постоянного тока.

Видно, что данные выражения для комплексов приведены в тригонометрической форме комплексного числа. Их также можно записать в алгебраической форме как a+jb.

Выражения для перехода из одной формы записи в другую также хорошо известны:

U_m (I_m)= (a²+b²) , arctg =b/a . Здесь a и b проекции отрезка на соответствующие оси координат (х, j).

Если на комплексной плоскости нанесены точки потенциалов с соединяющими их отрезками напряжения, то это будет потенциальная диаграмма напряжений. А если на комплексную плоскость нанести значения токов с присущими им направлениями, то это будет векторная диаграмма токов. Таким образом, мы получаем наглядный графический метод решения системы уравнений.

Мгновенное значение полной мощности в комплексной форме



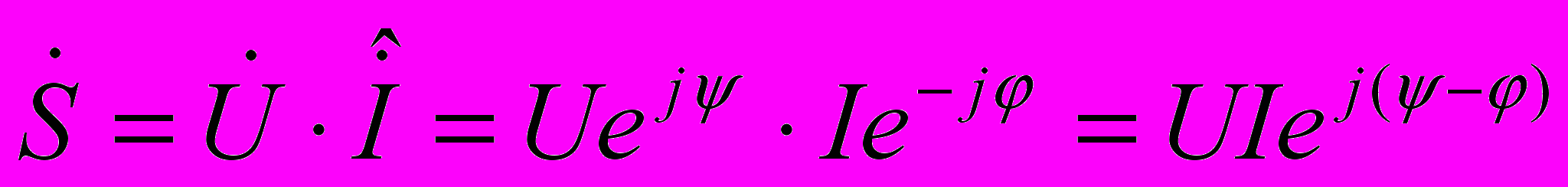
Здесь, чтобы получить более удобное в работе значение разности фаз (), взяли комплексно-сопряженное значение тока.

В алгебраической форме S =U  I cos() + j U  I sin()=Р+jQ ,

где Р= U  I cos() – активная мощность, а Q =U  I sin()=– реактивная.

Если учесть временную функцию е^jt , то мощность изменяется во времени как е^j2t.

Однако практически все нагрузки, особенно в силовой электротехнике, работают с постоянными времени много больше периода колебаний поступающего переменного тока. Поэтому на практике в энергосетях пользуются среднеквадратичным значением параметра, которое называют действующим или эффективным значением напряжения, тока или мощности и т.п.

Для гармонического сигнала среднеквадратичное значение, как нетрудно показать, равно



Отметим, что для обозначения амплитудного значения гармонического параметра применяют индекс m, в то время как для обозначения действующего значения никаких индексов не применяется из-за его большого практического использования.


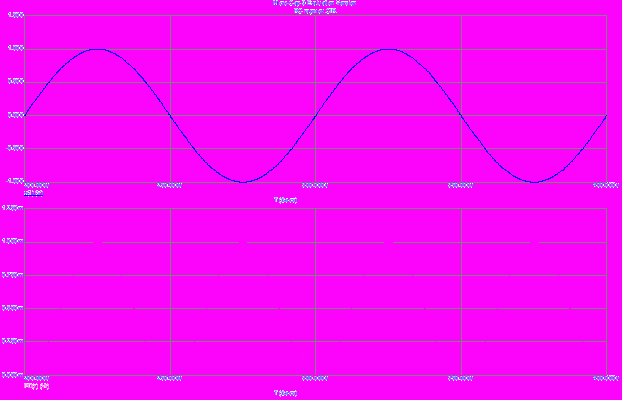
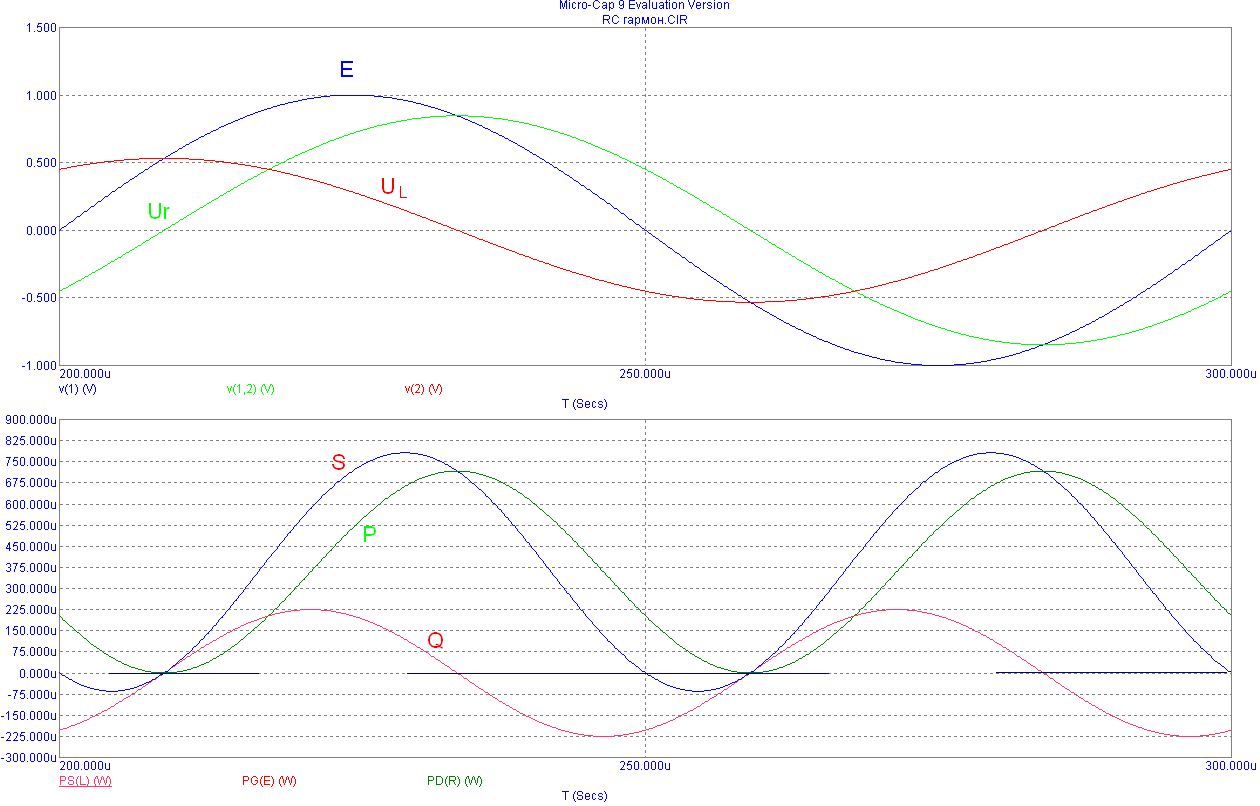
Здесь показано напряжение и активная мощность на сопротивлении R.

Таким образом, мы пришли к очень серьёзному выводу – в системе с гармоническим сигналом кроме активной мощности, постоянно находится и реактивная, которая, проходя через активные элементы, превращается в активную энергию, т.е. в тепло. Так реальные реактивные компоненты – конденсаторы и катушки индуктивности, всегда содержат в себе небольшую долю активного сопротивления (проводящие включения в материал диэлектрика или сопротивление проводов). Поэтому при больших уровнях реактивной мощности, развиваемой этими элементами, они могут существенно нагреваться, что, в свою очередь, может привести к физическому изменению свойств материалов, из которых они изготовлены. Просто говоря – сгореть. Например, категорически запрещается включать электролитический конденсатор в цепь переменного тока. Электролит содержит большие тяжёлые органические молекулы, которые на переменном токе начнут суетиться и толкаться, обеспечивая тем самым серьёзные активные потери. Из-за плохого теплоотвода произойдёт практически мгновенный нагрев электролитной жидкости до температуры кипения. И образовавшийся пар просто разорвёт тонкую алюминиевую колбу конденсатора, со всеми вытекающими тяжёлыми последствиями.

В то же время, наличие индуктивности и ёмкости в распределённой форме вызывает совсем другое распределение энергии в системе, чем при постоянном токе. Так, наличие емкости между проводами линии электропередачи и землёй приводит к существенным емкостным токам утечки энергии из системы, т.е. потерям. А незамкнутые магнитопроводы и одиночные провода с сильными токами создают в пространстве переменные магнитные поля, которые могут навести (индуцировать) токи в близлежащих металлических объектах, вызывая их нагрев и увеличивая активные потери в устройстве.

Но реактивная энергия не уходит из электрической системы, её уменьшение в одном месте компенсируется увеличением в другом. Гармоническое изменение потенциала одной точки приводит к соответствующему изменению потенциала соседней точки, т.к. между ними всегда действуют электрические силы или существует емкостная связь. Но точно таким же образом электрический ток в одном месте будет приводить к индуцированию тока по соседству за счёт действия магнитных сил, то есть возникает магнитная связь. Если не учитывать эти связи, а они порой не всегда очевидны в реальных устройствах, так как для осуществления этих связей нет необходимости устанавливать специальные проводники, то мы можем получить реактивную энергию в том месте, где её не ожидали. То есть у нас возникнут электромагнитные помехи, если эта реактивная энергия нам не нужна, и радиосвязь, если эту реактивную энергию использовать для передачи информации.

Два индуктивных элемента, объединённых магнитной связью, или магнитосвязаные катушки очень широко используют для гальванического разделения цепей и преобразования величин токов и напряжений (трансформатор).


Что же делает реактивная энергия в простейших цепях, содержащих один активный и один реактивный элемент?

Подключим RC-цепочку к источнику гармонического сигнала Е.




Уравнение, записанное в комплексах, выглядит следующим образом



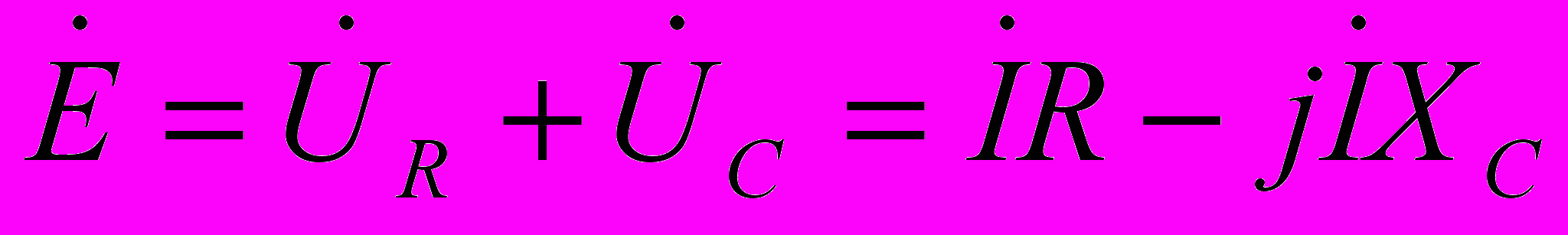
Отсюда 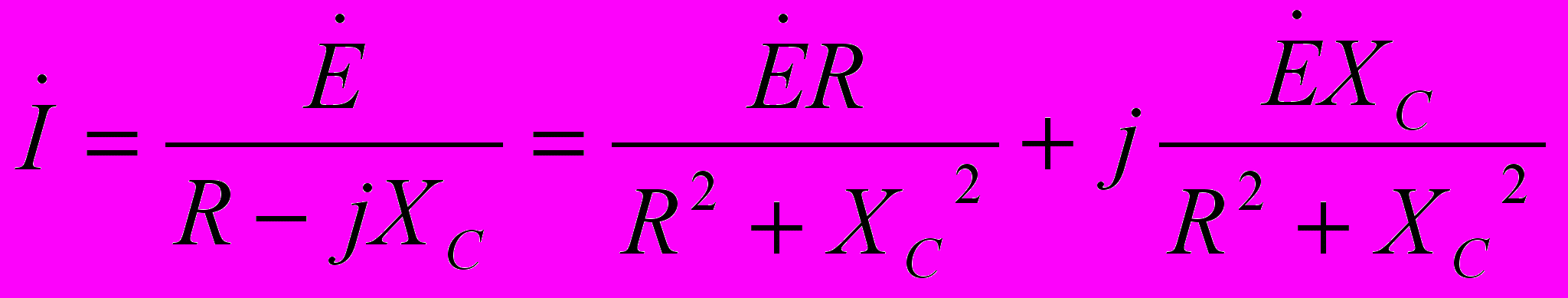, где реактанс X_C=1/С

Для указанных на схеме значений элементов и с учётом фазы источника равной 0


Х_С=1,6 кОм










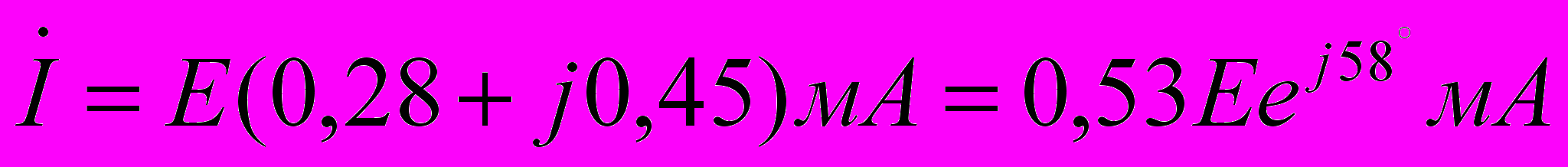
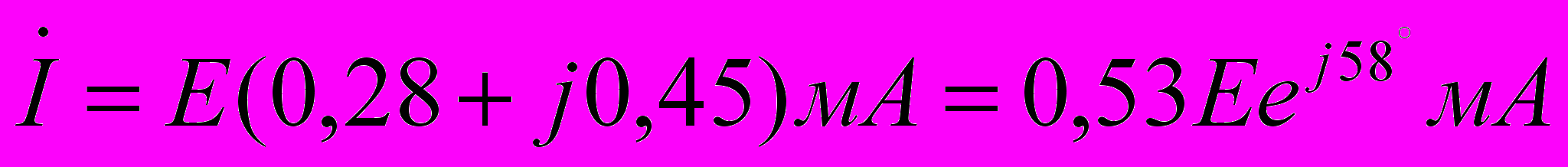
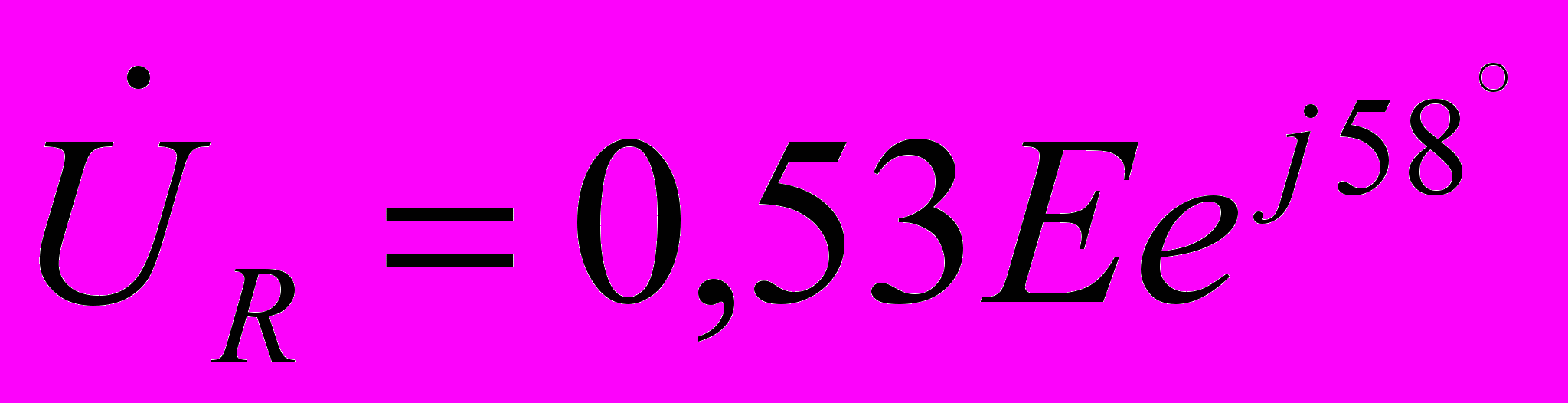
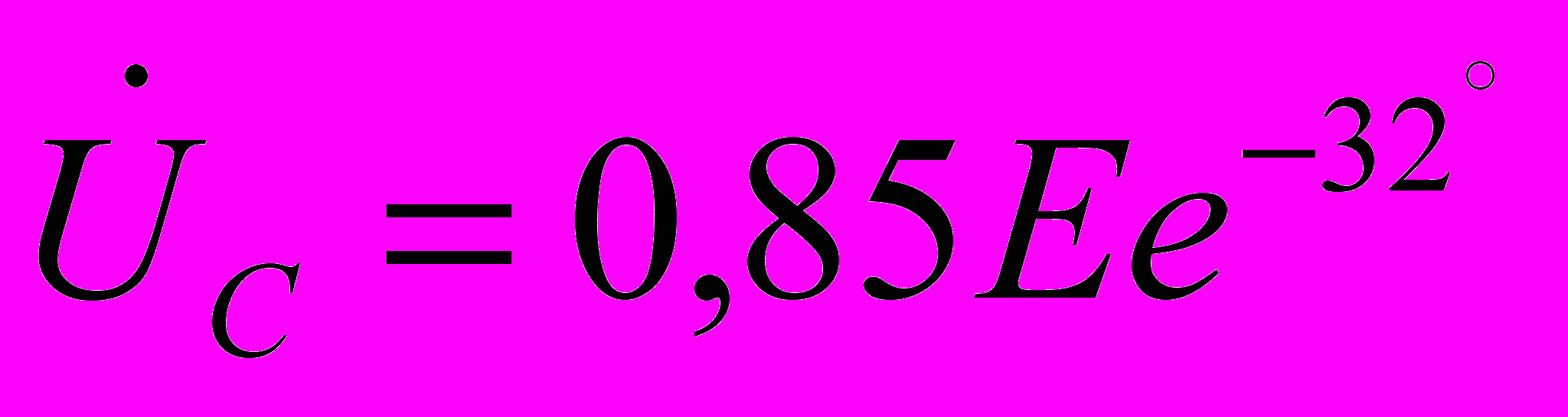
Модули мощности для этих данных Р=0.28 мВт и Q=0,45 мВАр.

Сдвиг фаз между ними /2.

На комплексной плоскости можно отложить значения модулей мощностей, тогда полная мощность будет являться их графической суммой. Мы получим так называемый треугольник мощностей, где P=Scosφ и Q=Ssinφ. Угол φ является разностью фаз между напряжением источника и протекающим через него током.





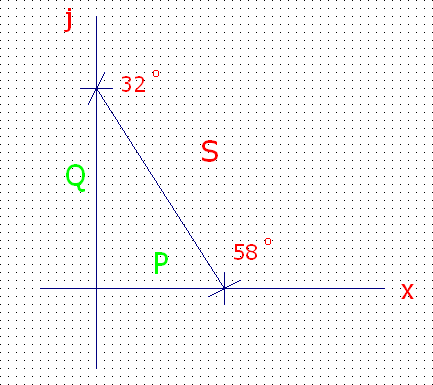
Ниже представлены временные развёртки тока напряжений на элементах U_R и U_C, а также э.д.с. источника и соответствующих мощностей.





Отсюда вытекают очень интересные заключения.

Во-первых, реактивная мощность в течение времени может быть отрицательной и положительной, в то время как активная мощность только положительная. То есть реактивный элемент в течение одного полупериода проходящего через него тока накапливает энергию и отдаёт её в цепь. Это обеспечивает протекание через ёмкость переменного электрического тока. В то же время переменные токи, проходя через конденсатор, совершают определённую механическую работу при перемещении зарядов между обкладками и нагревают этот компонент. Поэтому производители емкостных компонентов накладывают ограничения на величину переменных токов и их частоту.

Во-вторых, источником реактивной мощности являются реактивные элементы в нагрузке, которые обмениваются ею с источником. Протекающая через источник реактивная энергия вызывает дополнительные нагрузки в виде повышенных токов, что приводит к дополнительным потерям на внутреннем сопротивлении источника. Поэтому в силовой энергосети существует понятие фактора мощности, который при учёте одной частоты (основной гармоники) выражается через параметр cos φ=P/S. В соответствии с существующими правилами потребитель электроэнергии не должен допускать работу своего оборудования при значениях cos φ0,8, таким образом, поставщик накладывает ограничения на количество реактивной мощности генерируемой потребителем. В современной трактовке к этому правилу «cos φ» добавляют учёт токов гармоник основной частоты, которые тоже создаёт оборудование потребителя и которые также создают дополнительные нагрузки на оборудование поставщика электроэнергии. Поэтому растущую заботу о повышении фактора мощности иногда называют энергетической экологией.

В электронике, где имеют дело с передачей информационного сигнала в широкой полосе частот, важен такой параметр, как коэффициент передачи цепи К=U_вых/U_вх. В нашем случае 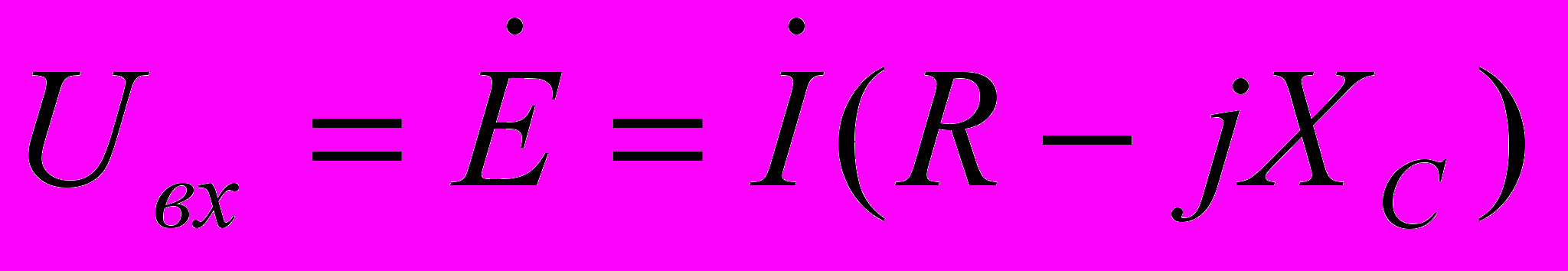, а 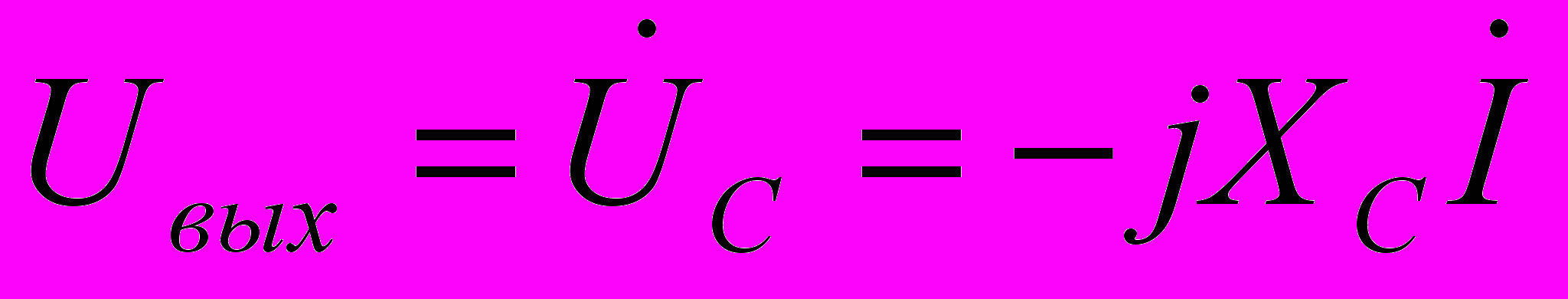. Тогда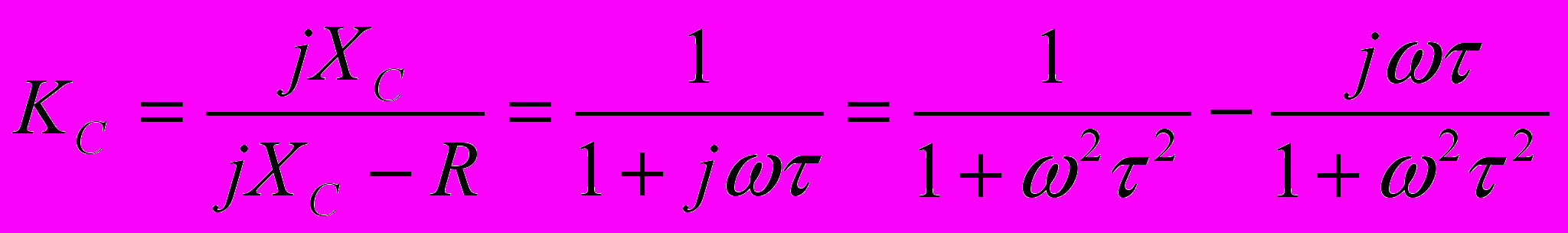



где τ = RC – постоянная времени RC-цепи.


Если исследовать значение модуля и фазы комплексного числа К(), то получим следующие амплитудно-частотные и фазочастотные характеристики, АЧХ и ФЧХ.





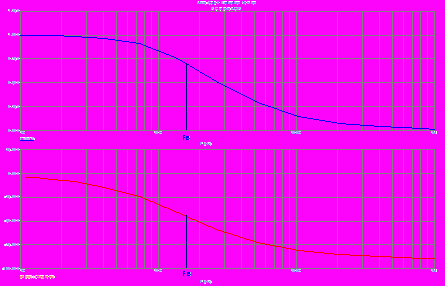
Здесь F_B верхняя граничная частота, при которой модуль К=1/2, а фаза φ= -/4. Это очень характерная точка, которая определяется из условия τ=1, или _в=1/τ. Её физический смысл в том, что при этой частоте реактивная энергия в RC-цепи равна активной. Отсюда видно, что все сигналы с частотами   Fв теряют незначительное количество энергии при прохождении этой цепочки. То есть RC-цепь в рассматриваемом варианте работает как низкочастотный фильтр. Если же в качестве выходного элемента рассматривать сопротивление, то получим высокочастотный фильтр.






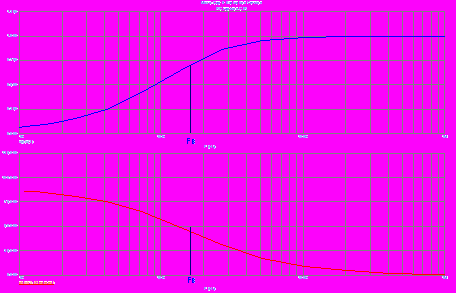
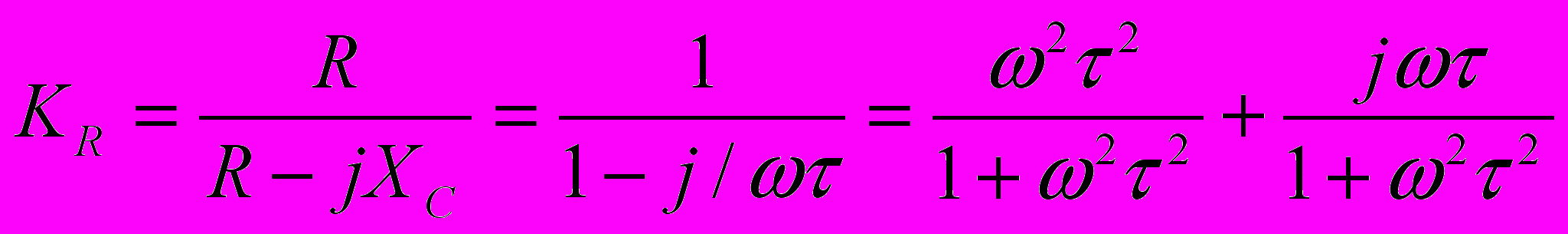
Если какую-либо функцию, представляющую электрический сигнал, разложить по гармоникам в виде ряда Фурье, то ограничение высоких частот свойственно операции интегрирования этой функции, а ограничение низких частот – её дифференцированию. Поэтому данные цепочки получили название, соответственно, интегрирующих и дифференцирующих. Данные математические свойства простых линейных электрических цепей, наряду с возможными другими математическими операциями, позволили создать довольно успешно работающие аналоговые вычислительные машины, которые в настоящее время практически вытеснены цифровой техникой.


Всё вышесказанное можно отнести и к RL-цепям.




Уравнение, записанное в комплексах, выглядит следующим образом



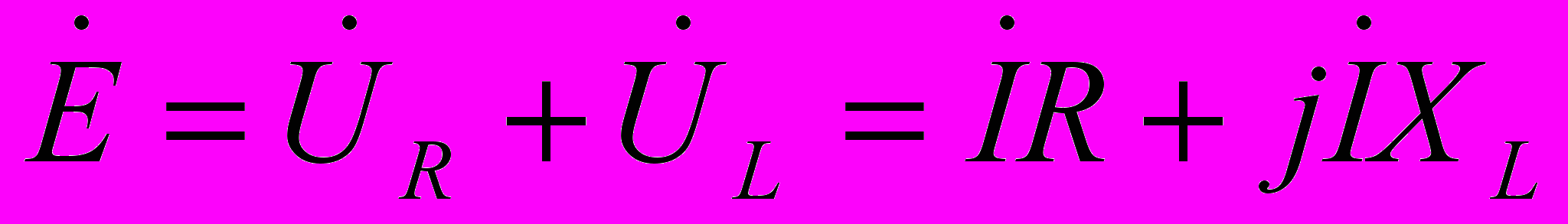
Отсюда 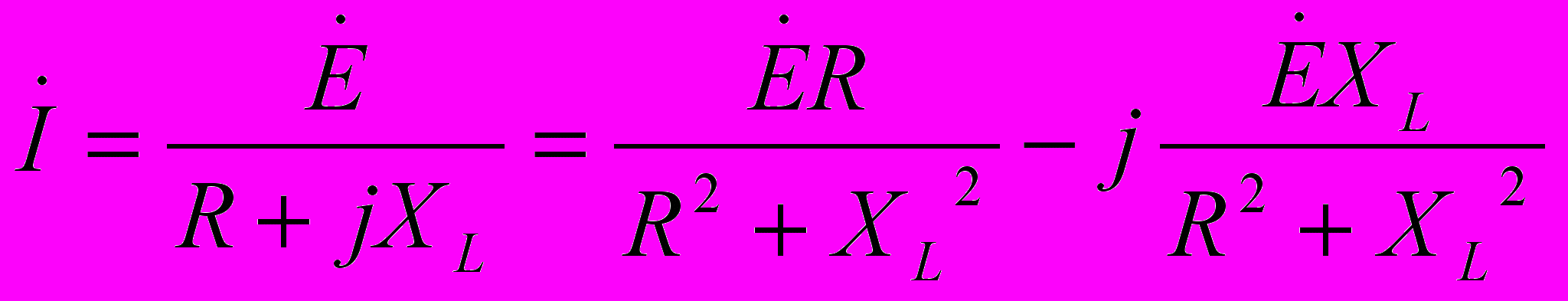, где реактанс X_L=L

Для указанных на схеме значений элементов и с учётом фазы источника равной 0


Х_L=0,63 кОм









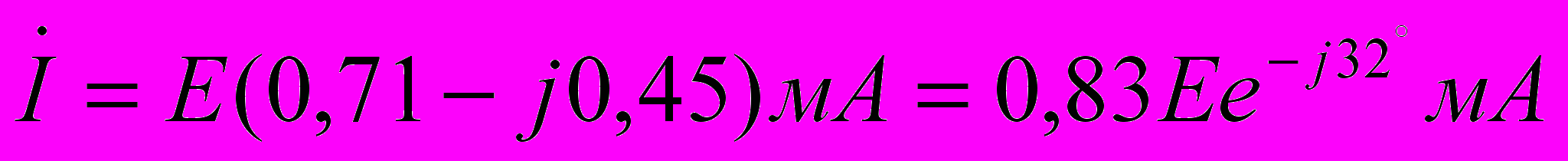
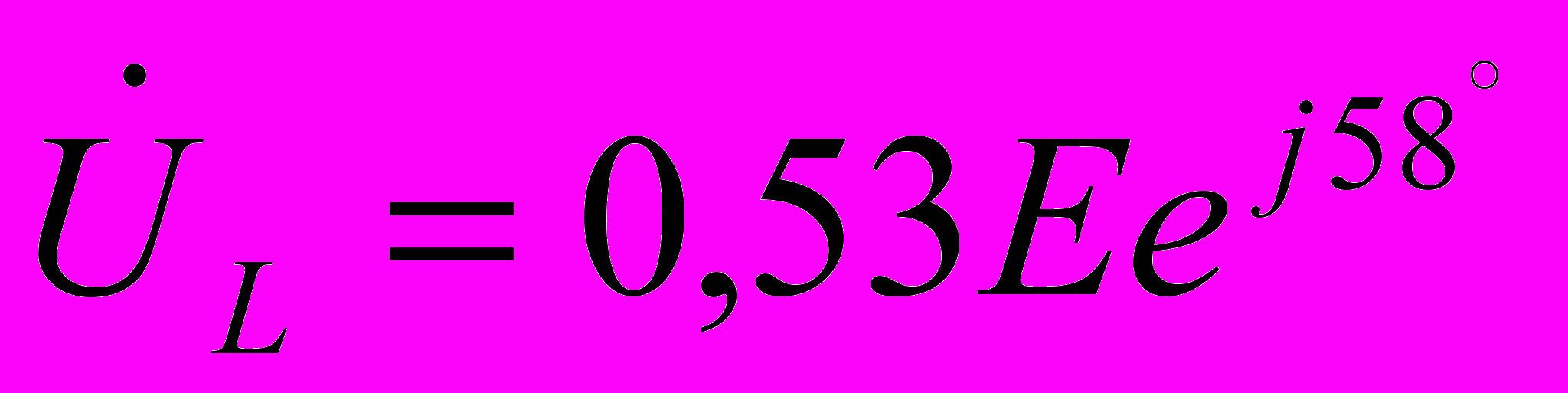
Модули мощности для этих данных Р=0.69 мВт и Q=0,44 мВАр.

Сдвиг фаз между ними /2.

Треугольник мощностей




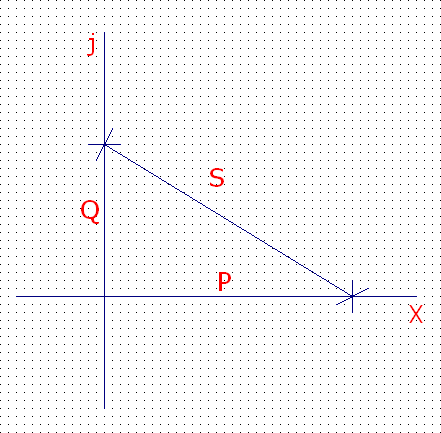
Ниже представлены временные развёртки тока напряжений на элементах U_R и U_L, а также э.д.с. источника и соответствующих мощностей





Гармонические колебания в электрических цепях открыли возможность применения очень интересного эффекта – электрического резонанса, при котором возможно накопление реактивной энергии в системе с гармоническим источником.

Рассмотрим простые задачи: последовательное и параллельное соединение всех трёх аналоговых элементов.

Простейшая схема последовательного соединения выглядит следующим образом





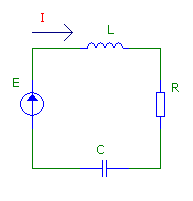
Из её анализа следует, что ток в контуре будет равен


= =


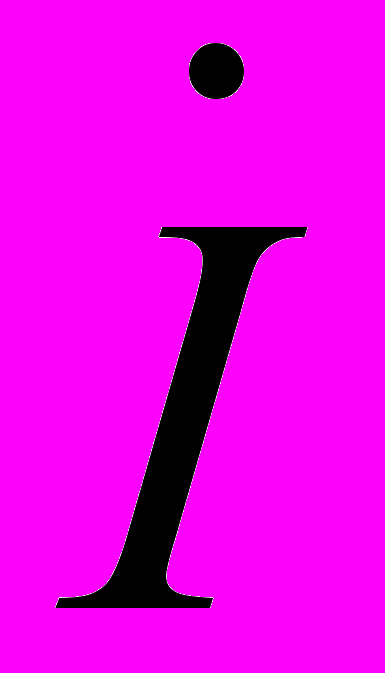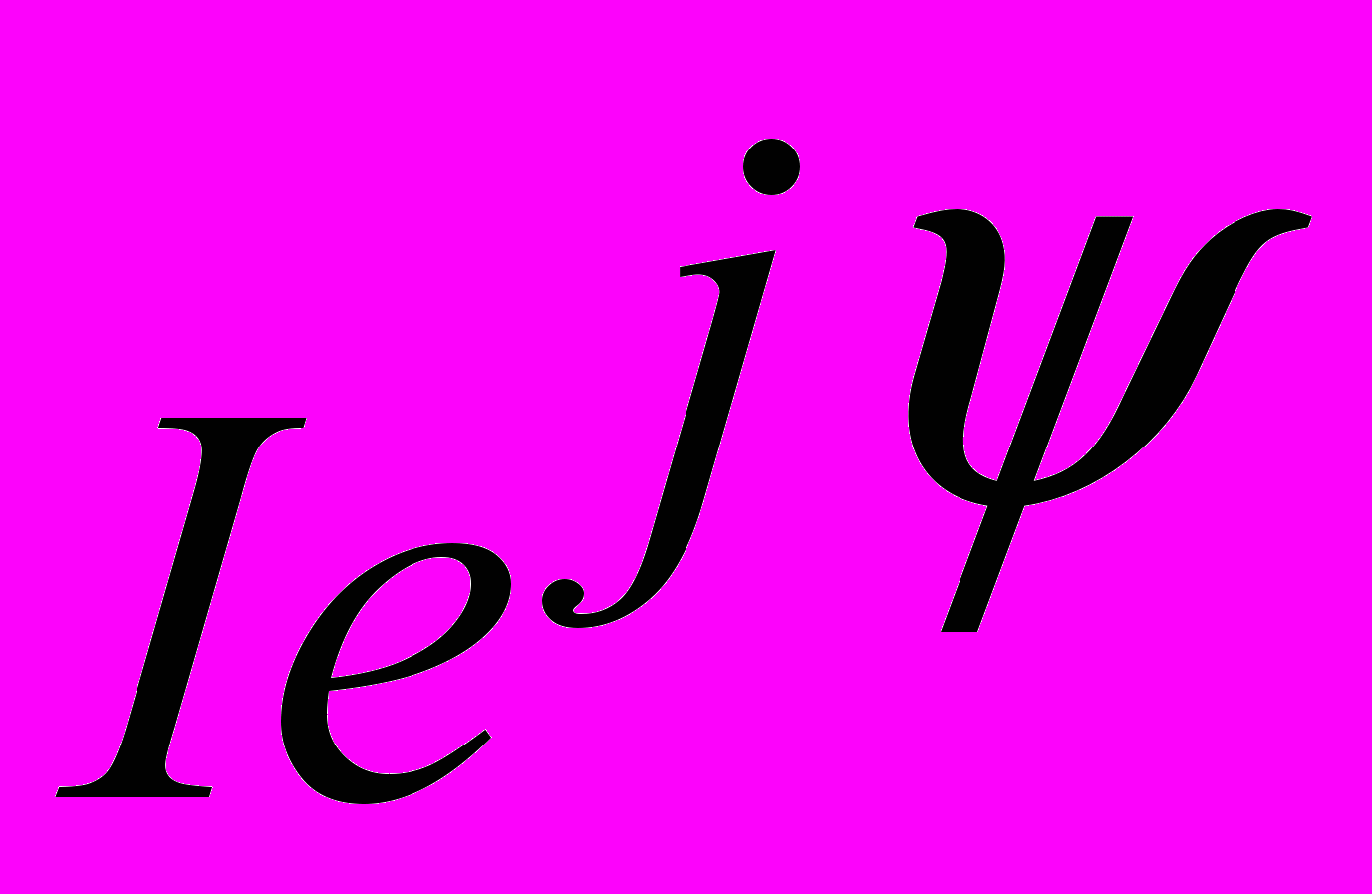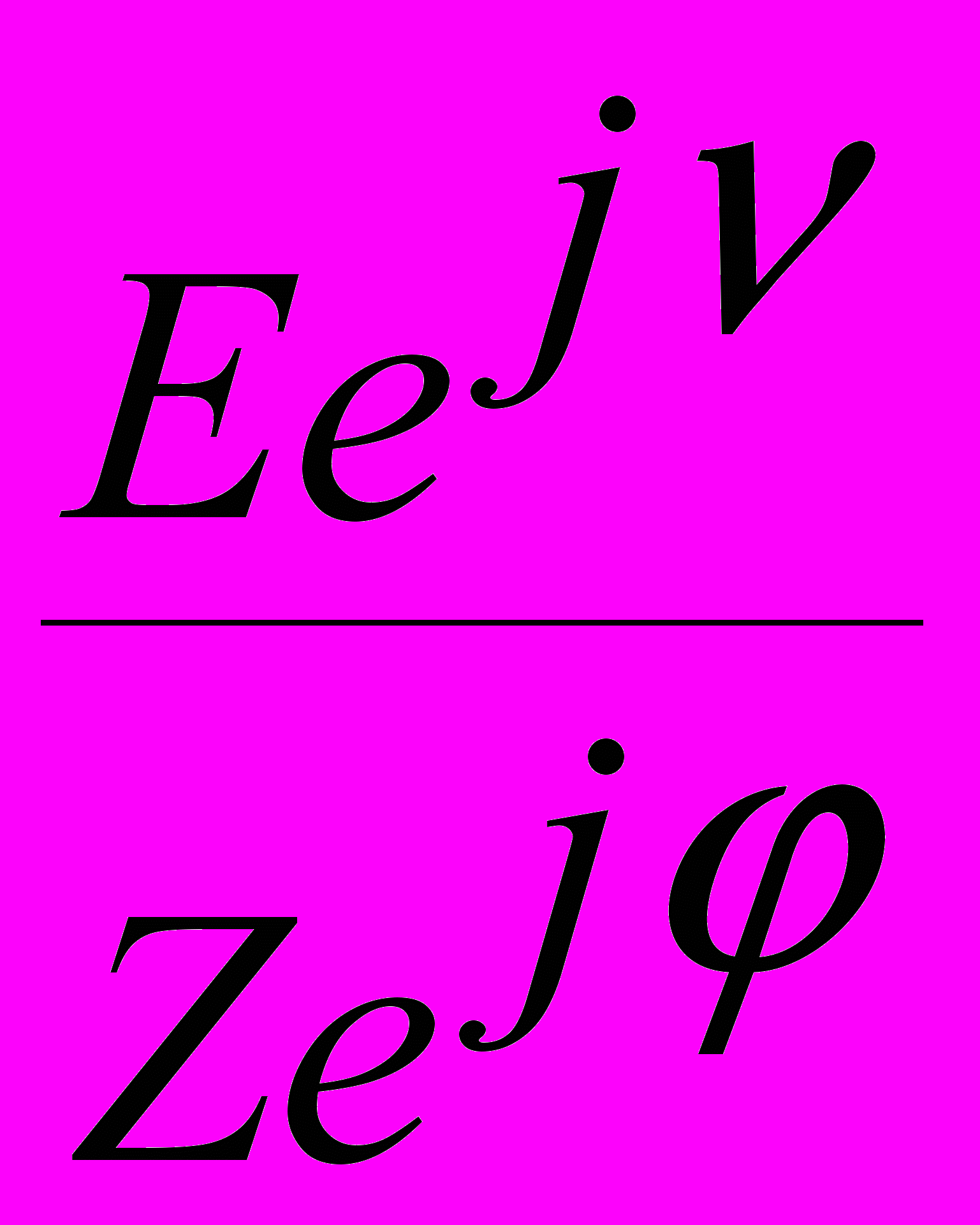
где 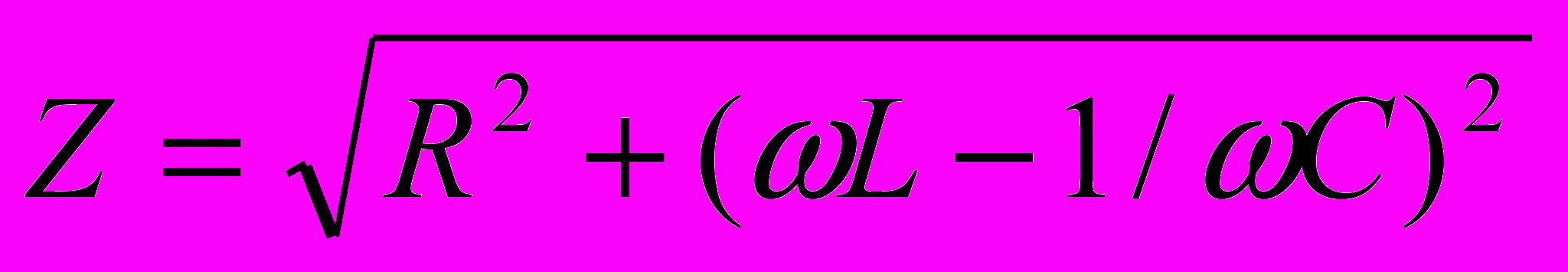- импеданс контура

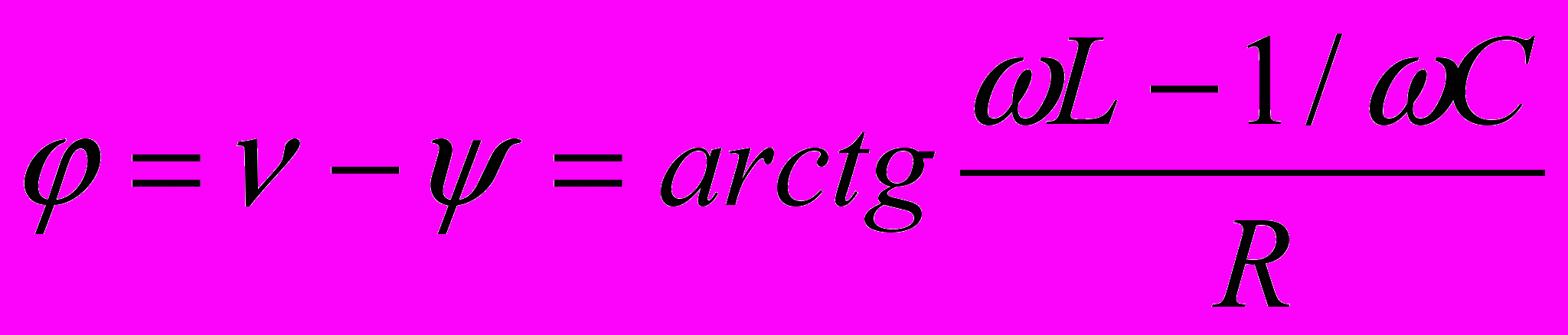- угол сдвига фаз между напряжением источника E и током в контуре I.

Отсюда видно, что при L=1/C импеданс Z будет иметь минимальное значение равное активному сопротивлению контура R. Мы получим явление резонанса в электрических цепях – увеличение токов и напряжений на отдельных участках цепи при изменении частоты гармонического сигнала. Физической основой резонанса в электрических цепях является обмен реактивной энергией между емкостными и индуктивными элементами, включенными в данную цепь. Если эта энергия проходит через источник (последовательное включение), то мы имеем так называемый резонанс напряжений (ImZ=0, мнимая часть полного сопротивления нагрузки равна 0), а если не проходит через источник (параллельное включение), то мы имеем резонанс токов (ImY=0, мнимая часть полной проводимости нагрузки равна 0).

При значении резонансной частоты




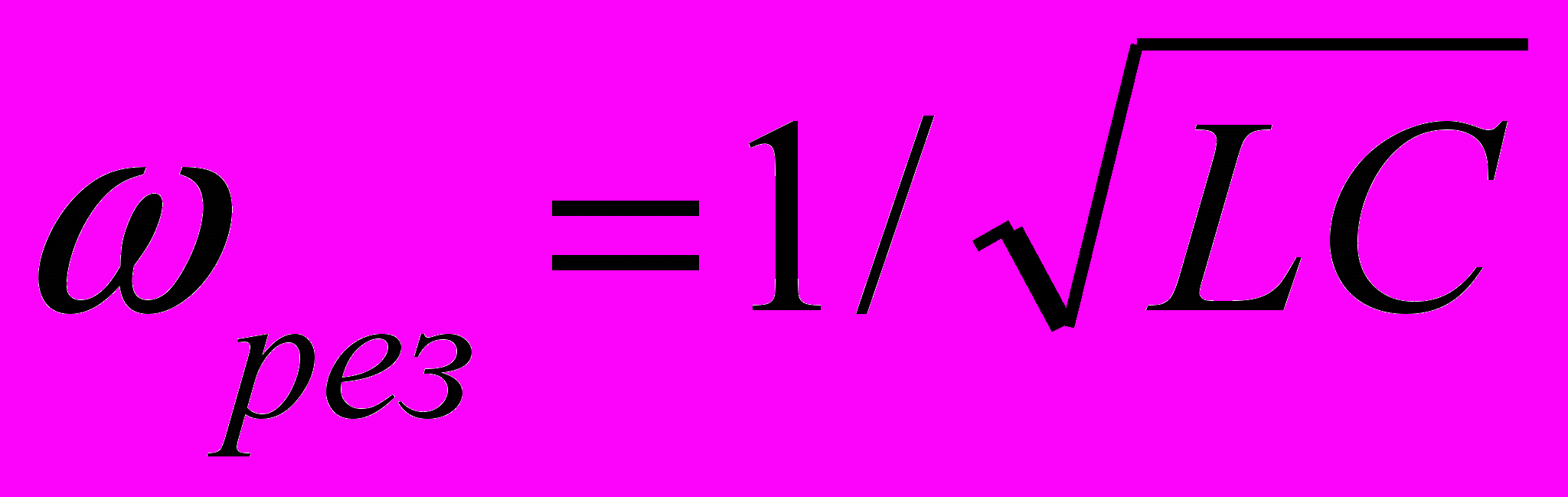
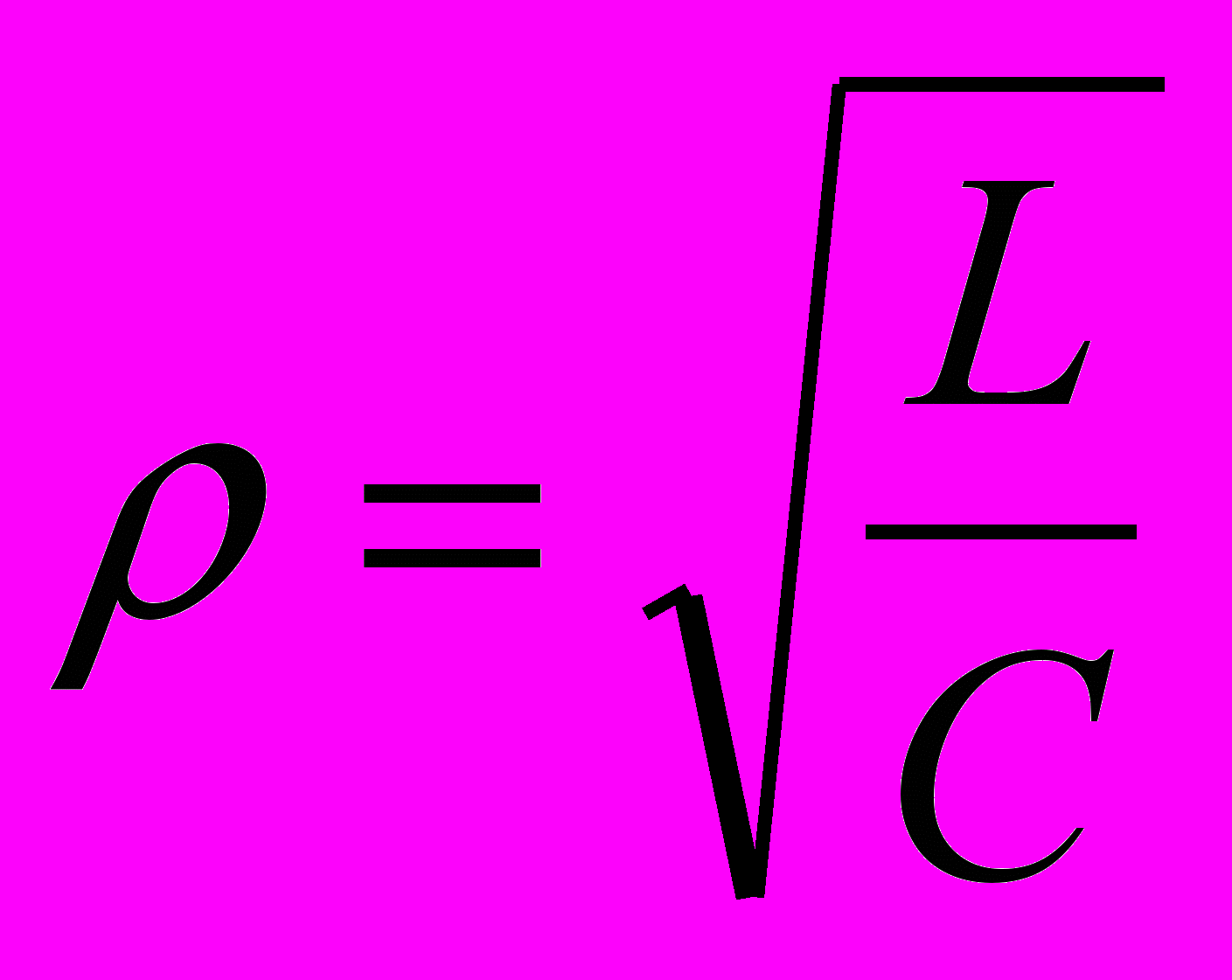
ток и напряжение совпадают по фазе, ток принимает максимальное значение Е/R, а

реактансы равны X_L=X_c=L/C=  . Эта величина называется характеристическим сопротивлением контура и имеет размерность Ом. Она характеризует количество реактивной энергии находящейся в контуре.


При резонансе в последовательной цепи напряжения на реактивных элементах могут превысить входное напряжение, если параметр добротности контура будет





Наибольшие значения напряжений на конденсаторе и индуктивности достигаются при частотах, несколько отличающихся от резонансной частоты.




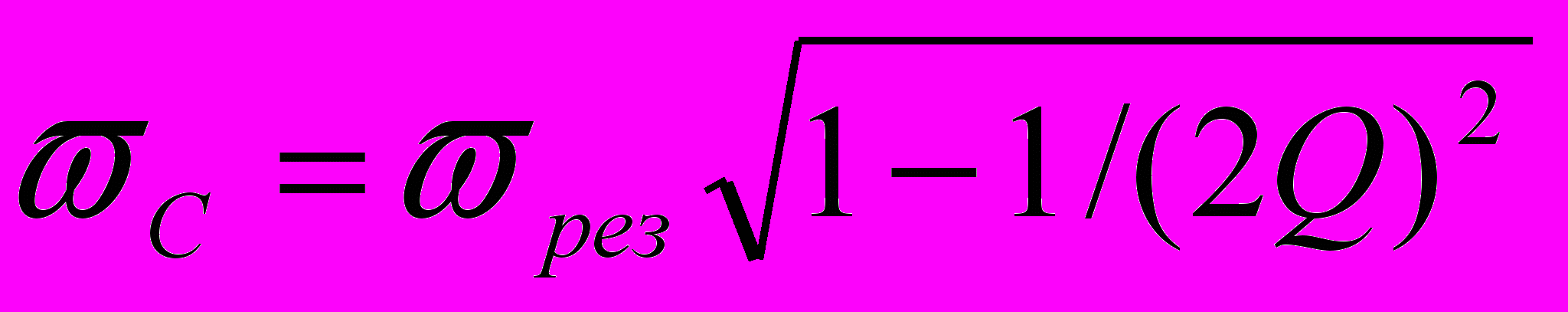
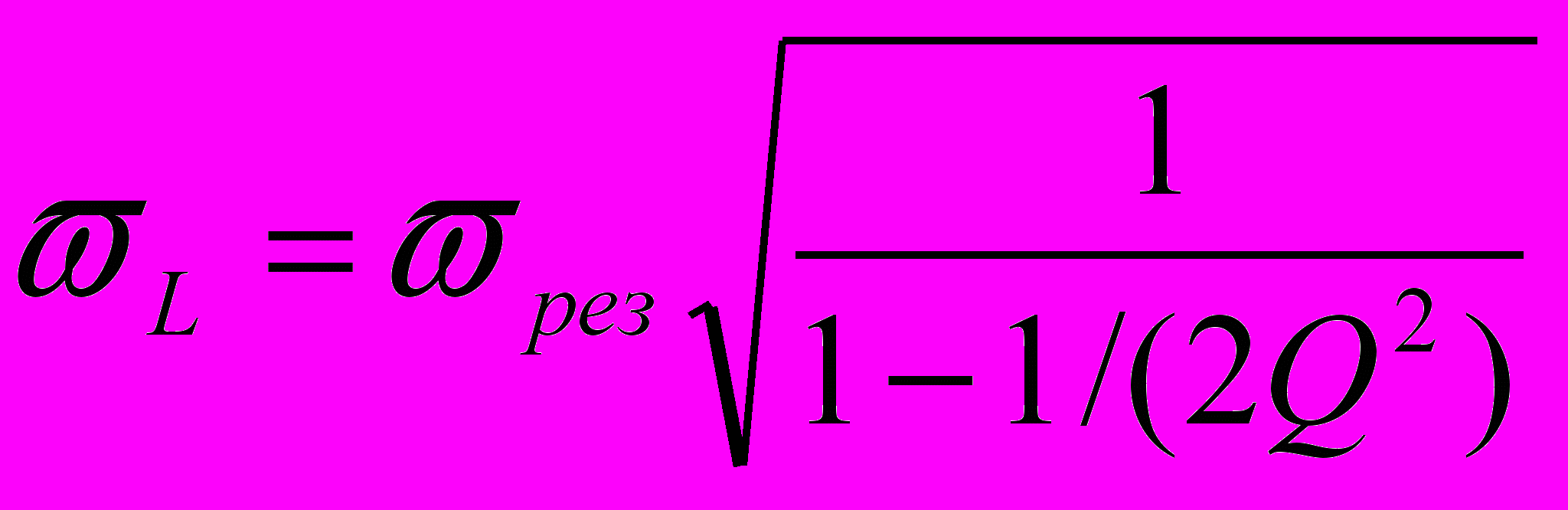
Название «резонанс напряжений» отражает тот факт, что действующие значения напряжений на реактивных элементах в момент резонанса равны (но противоположны по фазе) и могут в Q раз превышать значение э.д.с. источника.

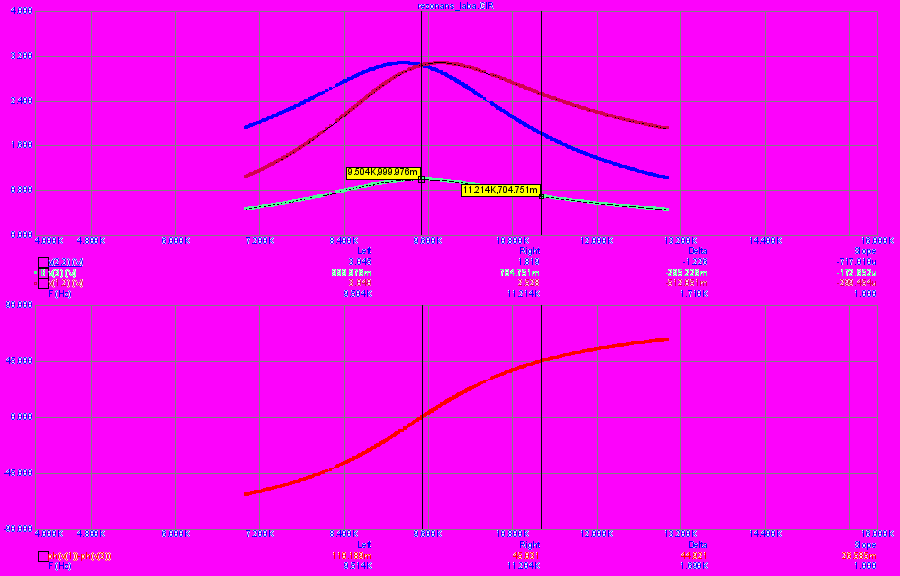
Рассмотрим зависимости от частоты действующего значения тока I (амплитудно-частотная характеристика, АЧХ) и разности фаз  между э.д.с. источника и током в контуре (фазочастотная характеристика, ФЧХ), которые приведены на рис.2.

Выделим на них две знаменательные точки – когда разность фаз  = ±/4. Эти точки аналогичны частоте F_в в рассмотренных ранее простых RC- и RL-цепочках, то есть при этих частотах активная энергия в контуре равна реактивной.

При этих частотах (₁ и ₂)

, и величина тока будет в 2 раз меньше амплитудного значения.

Разность частот = ₁ - ₂ называется полосой пропускания, а величина

S= называется затуханием контура.

Границы полосы пропускания можно определить по соотношению

Переход от первичных параметров аналоговых элементов L, C, R к вторичным параметрам, а именно - резонансной частоте _рез, добротности Q и полосе пропускания , очень важен с практической точки зрения. В значения параметров элементов, кроме электрических характеристик материалов, входят трудно определяемые размеры пространства, занятого электромагнитным полем, особенно, когда невозможно выделить соответствующие компоненты в виде отдельных конструктивных деталей. А вторичные параметры непосредственно измеряются и несут в себе информацию, необходимую конструктору электрических устройств.





Простейшая схема параллельного соединения выглядит следующим образом




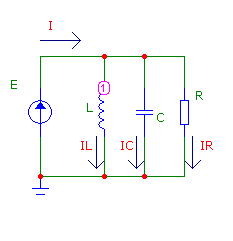
Из её анализа следует, что ток источника будет равен





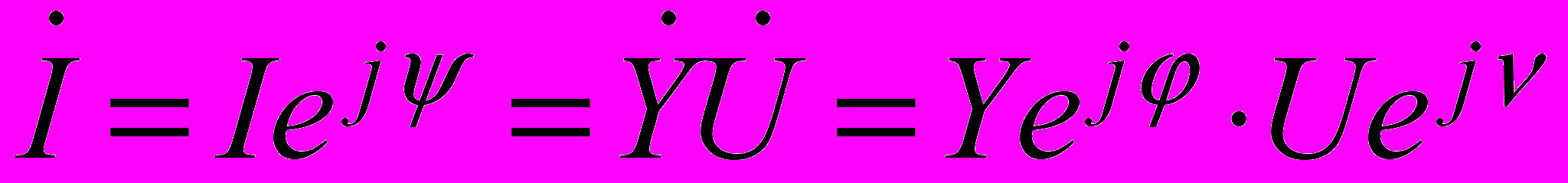
где - полная проводимость цепи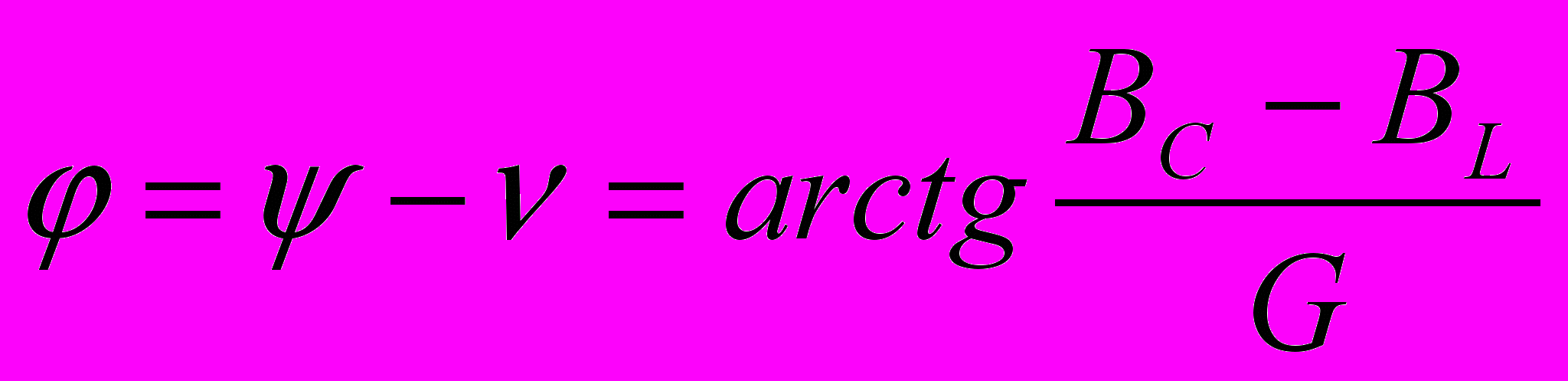

- угол сдвига фаз между общим током и напряжением источника Е.

При угловой частоте

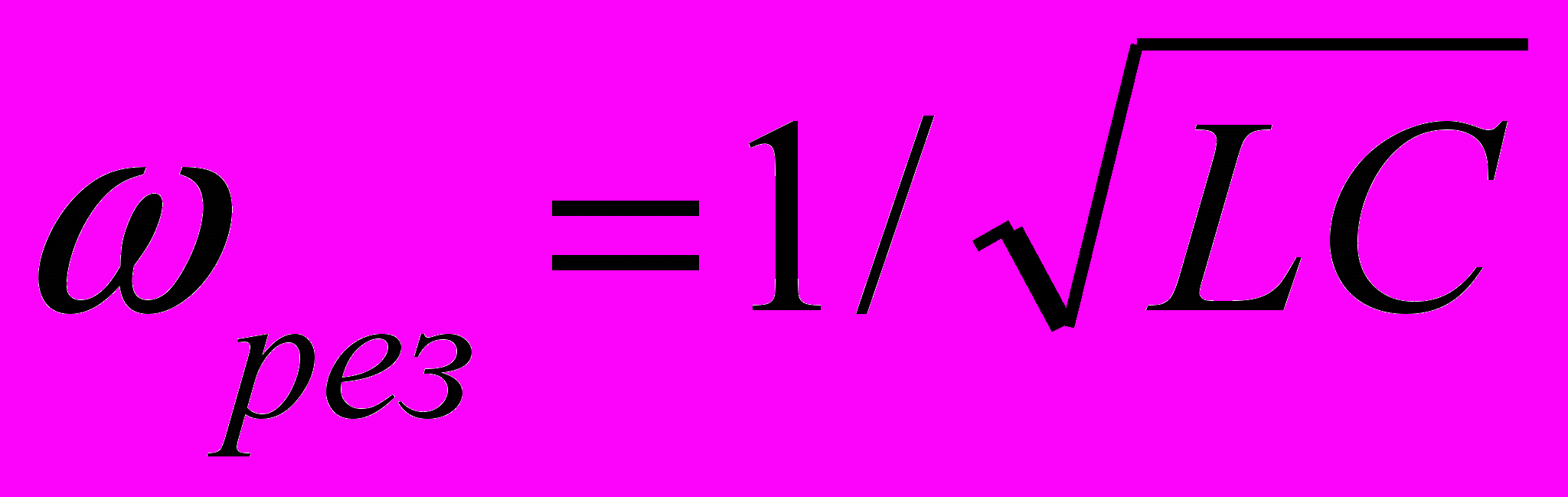
Реактансы параллельных ветвей с реактивными элементами одинаковы X_L=X_C= L/C , общий ток и напряжение источника совпадают по фазе, причём общий ток принимает минимальное значение GU=U/R.

Название «резонанс токов» отражает равенство действующих значений токов в индуктивном и емкостном элементах в момент резонанса (но противоположны по фазе) и могут в Q раз превышать значение общего тока

при противоположных фазах.

Если вместо источника э.д.с. применить источник тока, то при малых значениях тока источника можно достичь значительного увеличения токов в ветвях с реактивными элементами.

Рассмотрим зависимости от частоты действующего значения общего тока I (амплитудно-частотная характеристика, АЧХ) и разности фаз  между э.д.с. источника и общим током (фазочастотная характеристика, ФЧХ), которые приведены на рис.4.

Выделим на них две знаменательные точки ₁ и ₂ – когда разность фаз  = ±/4.

При этих частотах активная проводимость будет равна реактивной , и величина общего тока будет в 2 раз больше минимального значения. Здесь также полностью применимы понятия полосы пропускания  и затухания контура S. Следует обратить внимание, что при резонансе тока измерять полосу пропускания по АЧХ достаточно трудно, особенно при высоких значениях добротности.





Чтобы использовать явление резонанса, необходимо иметь генераторы гармонических колебаний с широким набором частот, лучше даже плавно перестраиваемой частоты. Так как на линейных элементах это сделать нельзя, то начали изобретать различные нелинейные элементы и схемы с их использованием. В начале появились электромеханические устройства. Первым их стал использовать Никола Тесла для получения высоких напряжений в колебательных контурах (трансформатор Тесла или два магнито-связаных колебательных контура). С их помощью ему удалось создать люминесцентный источник света, демонстрация которого оказывала в те тёмные времена потрясающее впечатление на публику. В 1988 году Генрих Герц, используя колебательные контура в качестве источника и приёмника высокочастотного гармонического сигнала, продемонстрировал возможность его передачи на расстояние без проводов по ёмкостной связи. И стало ясно, что при расстояниях много больше длины волны гармонического сигнала, электрическое поле успевает преобразоваться в магнитное и обратно. Так родилась радиотехника с её электромагнитными волнами.

В дальнейшем появились генераторные и усилительные электронные лампы, что позволило создать мощные источники гармонических колебаний одновременно с чувствительными приёмниками и охватить радиосвязью весь мир. Приход полупроводников существенно снизил размеры передающих и принимающих устройств и, в результате, мобильная связь стала неотъемлемым условием нашего образа жизни. Были созданы ламповые генераторы в гигагерцовой области частот, что привело к созданию сверхвысокочастотной техники, в которой длина волны сравнима с размерами самого устройства. А далее были созданы генераторы в миллиметровой (мазеры) и даже в световой (лазеры) области частот с передачей этих сигналов по оптоволокну.

Естественно, для создания электротехнических устройств этого уровня нужно использовать уравнения Максвелла, так как аналоговый поход с токами инапряжениями приводит к уравнениям с матрицами практически бесконечного порядка. А это привело к тому, что электротехники, работающие в разных частотных диапазонах, перестали понимать друг друга. Появились электрики и электронщики, радиотехники и «СВЧ-шники», а позднее и «цифровики» с программистами.