Решение. Метод контурных токов
| Вид материала | Решение |
Содержание2. Метод узловых потенциалов. 3. Метод эквивалентного генератора. |
- Решение. Из анализа схемы следует, что резисторы, 80.22kb.
- Задание: Составить систему уравнений по законам Кирхгофа для расчета токов ветвей., 17.99kb.
- Программное обеспечение приборов неразрушающего контроля, реализующих метод вихревых, 101.12kb.
- Isbn 978-5-7262-1375 нейроинформатика 2011, 79.42kb.
- Гармонический сигнал основная форма токов в электросиловых цепях. Метод комплексных, 165.53kb.
- Лекция 1, 259.64kb.
- Линейных алгебраических уравнений ax=B, где, 66.22kb.
- Методика №6 Измерение напряжений и токов питающей сети москва, 70.72kb.
- Проектный метод в деятельности доу, 214.46kb.
- Проектный метод в деятельности доу, 187.91kb.


Решение.
1. Метод контурных токов.
1. Изображаем схему цепи в соответствии с исходными данными. Обозначаем узлы. Произвольно выбираем и показываем направления контурных токов (одним из контурных токов выбираем ток источника).
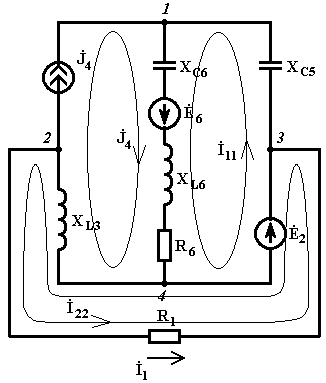
2. Для контурных токов составляем систему уравнений по второму закону Кирхгофа.
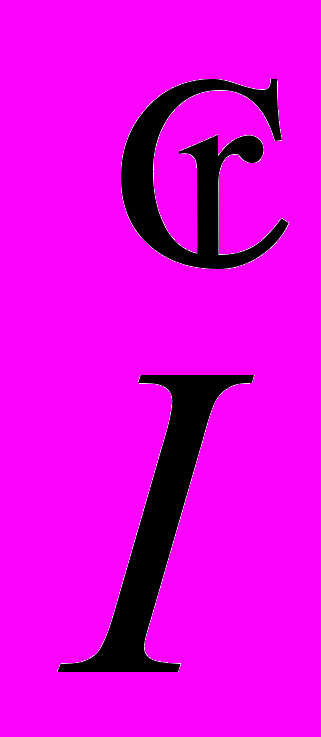 11∙(-jXC5 - jXC6 + jXL6 + R6) +
11∙(-jXC5 - jXC6 + jXL6 + R6) +  4∙(-jXC6 + jXL6 + R6) =
4∙(-jXC6 + jXL6 + R6) = 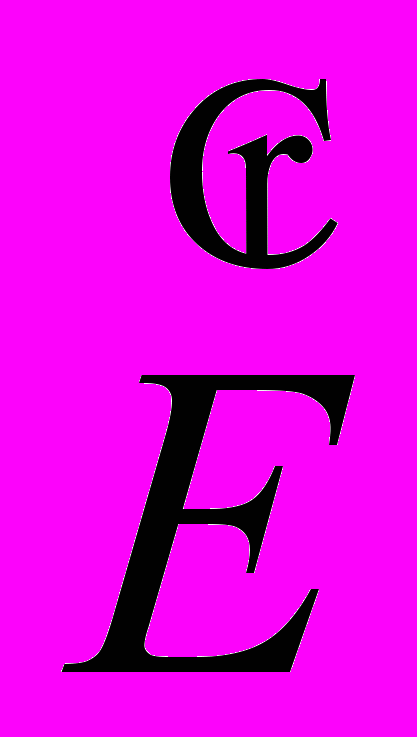 2 +
2 + 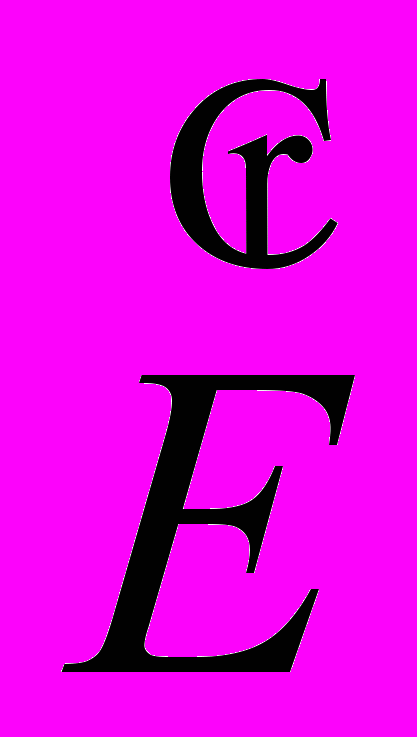 6
6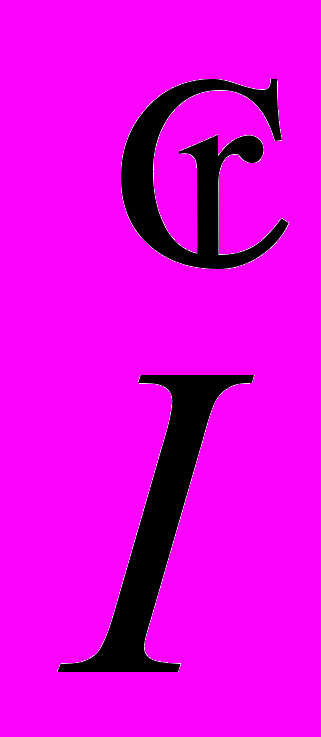 22∙(R1 + jXL3) +
22∙(R1 + jXL3) +  4∙jXL3 = -
4∙jXL3 = -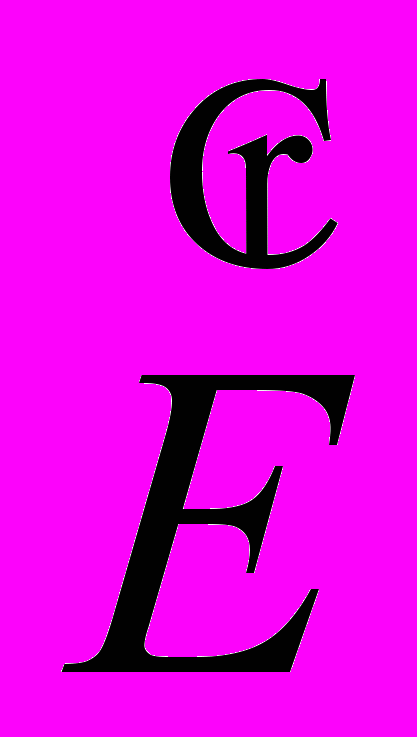 2
23. Поскольку по заданию требуется найти только ток в первой ветви, достаточно найти только второй контурный ток, т.е. использовать только второе уравнение системы.
Подставляем численные значения, вычисляем коэффициенты и находим контурный ток.
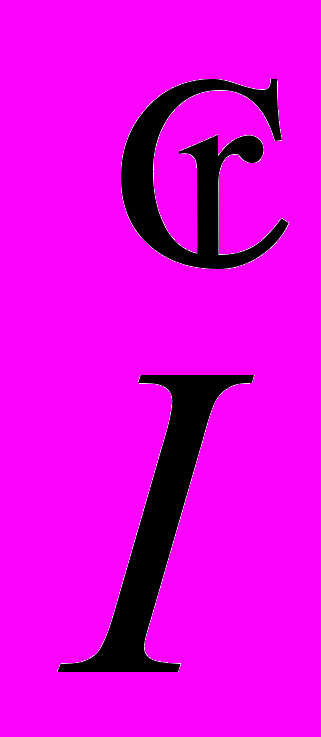 22∙(10 + j10) + (5 + j5)∙j10 = -100
22∙(10 + j10) + (5 + j5)∙j10 = -100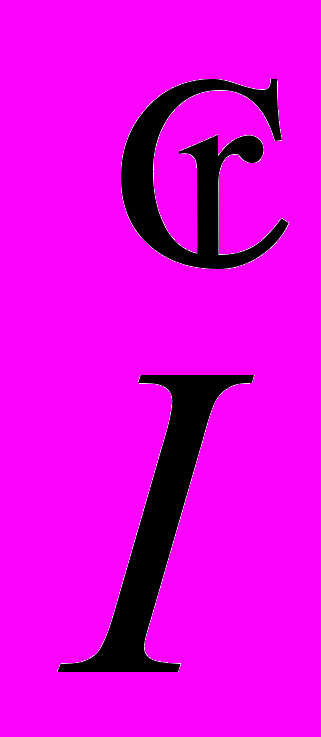 22∙(10 + j10) = -50 - j50
22∙(10 + j10) = -50 - j50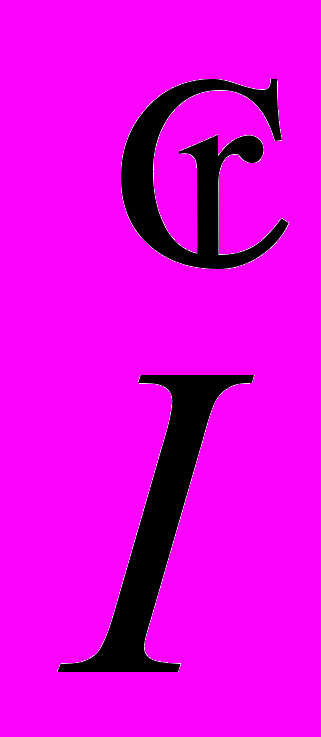 22 = (-50 - j50)/(10 + j10) = -5 = 5∙ej180°
22 = (-50 - j50)/(10 + j10) = -5 = 5∙ej180°4. Руководствуясь принципом наложения окончательно получаем
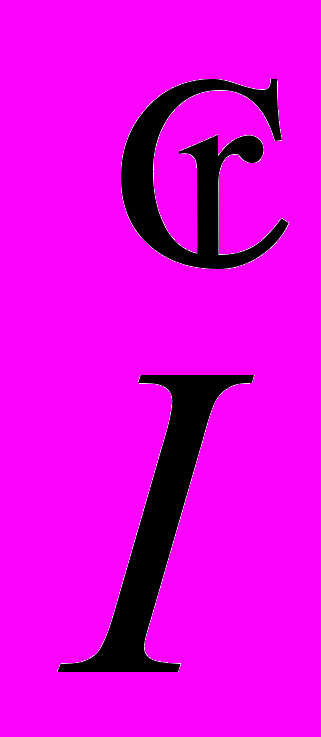 1 =
1 = 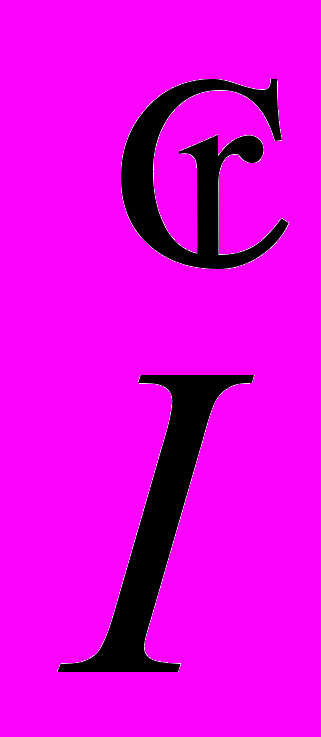 22 = -5 = 5∙ej180° [А]
22 = -5 = 5∙ej180° [А]2. Метод узловых потенциалов.
1. Принимаем потенциал узла "4" условно равным нулю (
 4 = 0)
4 = 0)
2. Составляем систему уравнений для узловых потенциалов в общем виде
 1∙Y11 +
1∙Y11 +  2∙Y12 +
2∙Y12 +  3∙Y13 =
3∙Y13 = 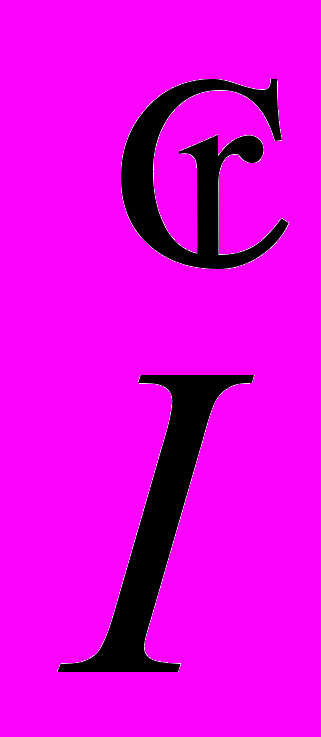 11
11 1∙Y21 +
1∙Y21 +  2∙Y22 +
2∙Y22 +  3∙Y23 =
3∙Y23 = 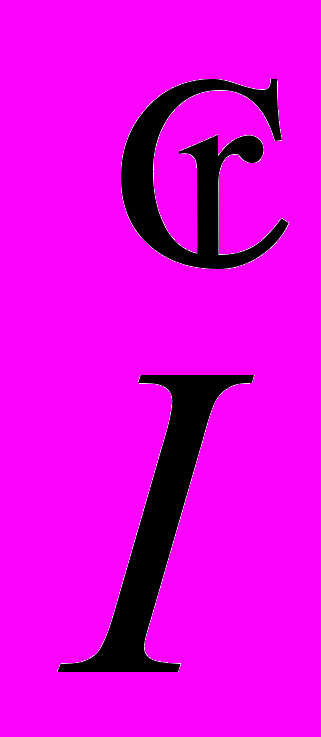 22
22 1∙Y31 +
1∙Y31 +  2∙Y32 +
2∙Y32 +  3∙Y33 =
3∙Y33 = 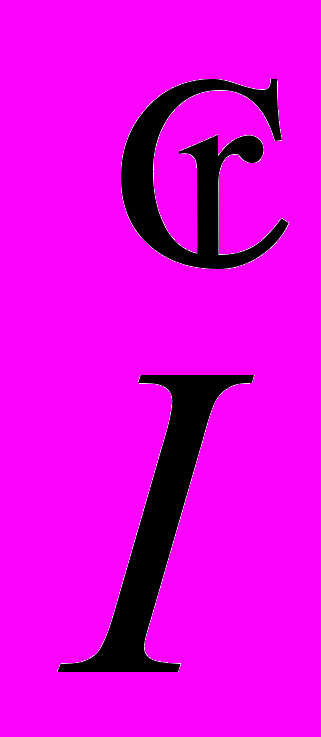 33
333. Анализируя схему видим, что между узлами "3" и "4" включен идеальный источник напряжения с нулевым внутренним сопротивлением, поэтому Y33 = ∞, а
 3 =
3 =  4 +
4 + 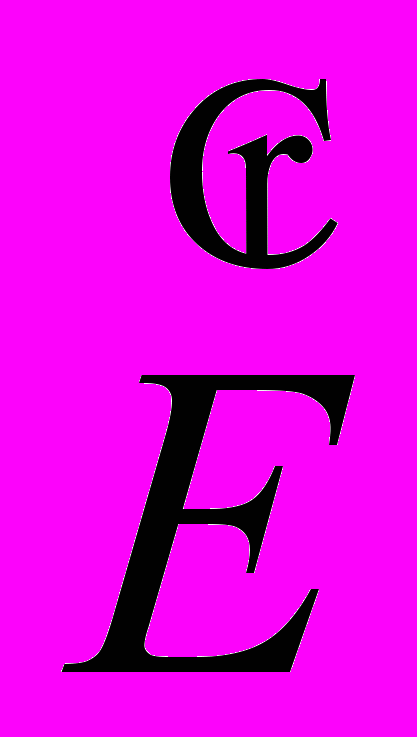 2 = 0 +
2 = 0 +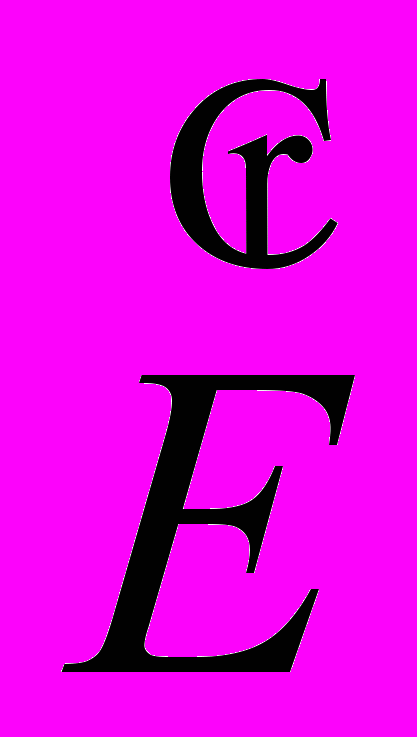 2 =
2 = 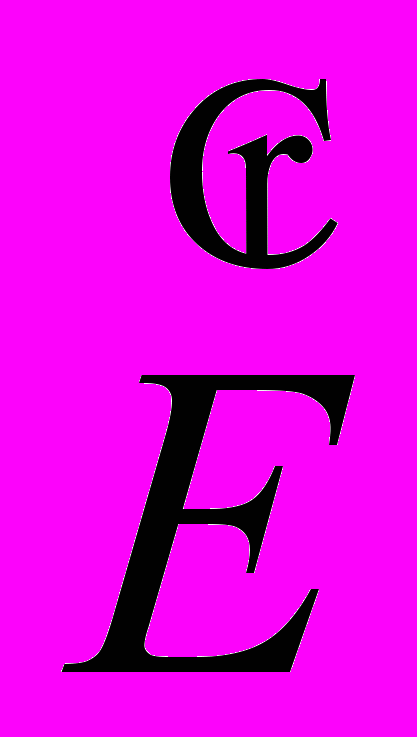 2.
2. Преобразовываем третье уравнение (избавляемся от потенциалов первого и второго узлов).
 1∙Y11 +
1∙Y11 +  2∙Y12 +
2∙Y12 +  3∙Y13 =
3∙Y13 = 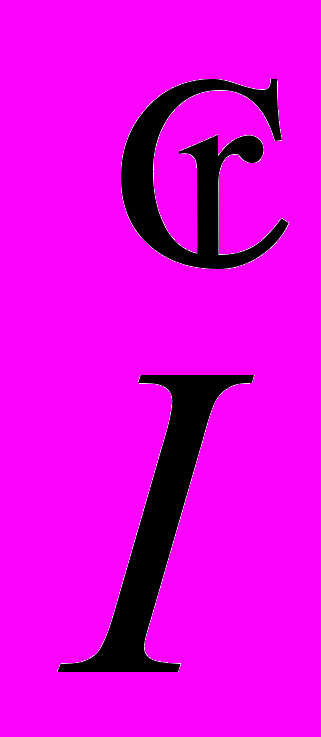 11
11 1∙Y21 +
1∙Y21 +  2∙Y22 +
2∙Y22 +  3∙Y23 =
3∙Y23 = 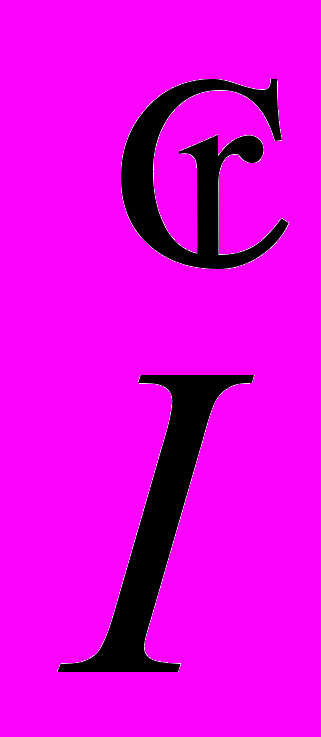 22
22 1∙0 +
1∙0 +  2∙0 +
2∙0 +  3∙1 =
3∙1 = 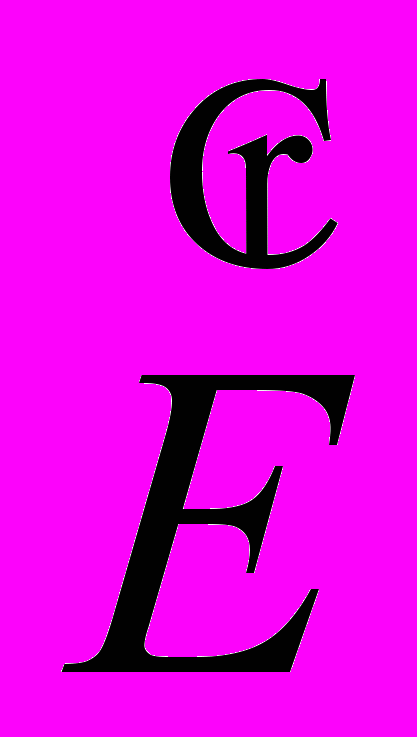 2
2здесь Ykk – собственные проводимости узлов (сумма проводимостей всех ветвей, подключенных к узлу k).
Ykh – взаимные проводимости узлов (сумма проводимостей всех ветвей, соединяющих узлы k и h, взятая с обратным знаком).
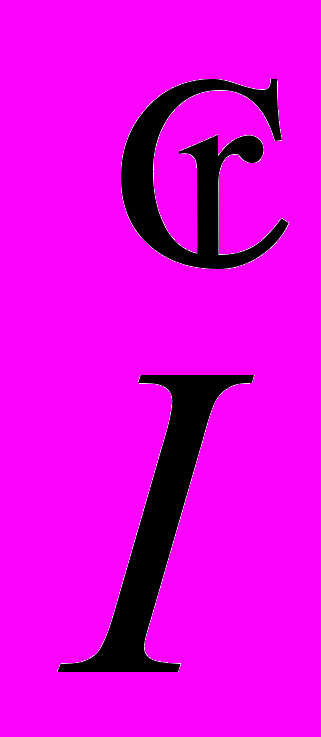 kk – узловые токи (алгебраическая сумма токов всех источников, подключенных к узлу k, при условном отсутствии разности потенциалов между узлами).
kk – узловые токи (алгебраическая сумма токов всех источников, подключенных к узлу k, при условном отсутствии разности потенциалов между узлами).Y11 = 1/(-jXC5) + 1/(-jXC6 + jXL6 + R6) = 1/(-j10) + 1/(-j25 + j35 +10) =
= 0,05 + j0,05 = 0,07071∙ej45°
Y22 = 1/R1 + 1/jXL3 = 1/10 + 1/j10 = 0,1 - j0,1 = 0,1414∙e-j45°
Y12 = Y21 = -1/∞ = 0
Y13 = -1/(-jX+) = -1/(-j10) = -j0,1 = 0,1∙e-j90°
Y23 = -1/R1 = -1/10 = -0,1 = 0,1∙ej180°
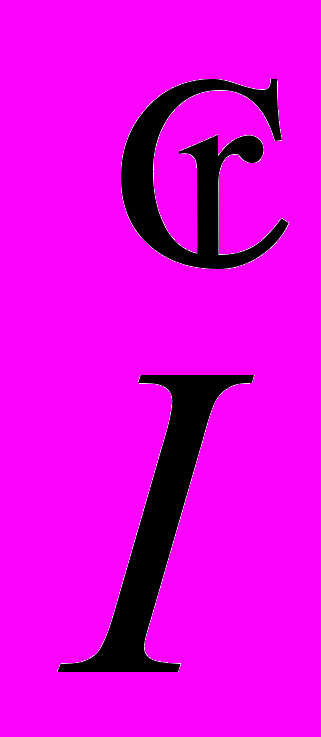 11 = -
11 = -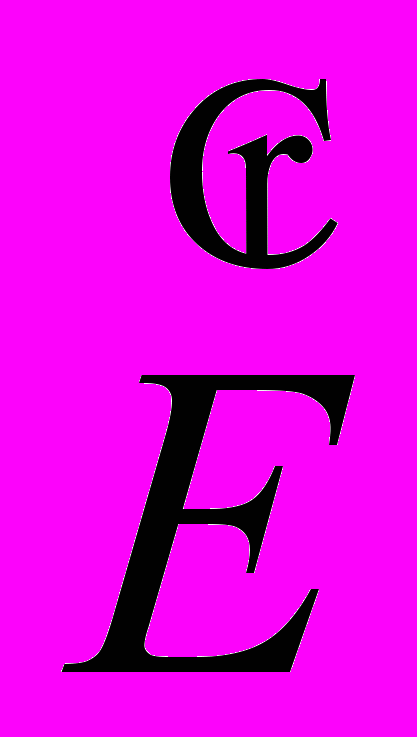 6/(-jXC6 + jXL6 + R6) +
6/(-jXC6 + jXL6 + R6) +  4 = -j100/(-j25 + j35 +10) + 5 + j5 = 0
4 = -j100/(-j25 + j35 +10) + 5 + j5 = 0 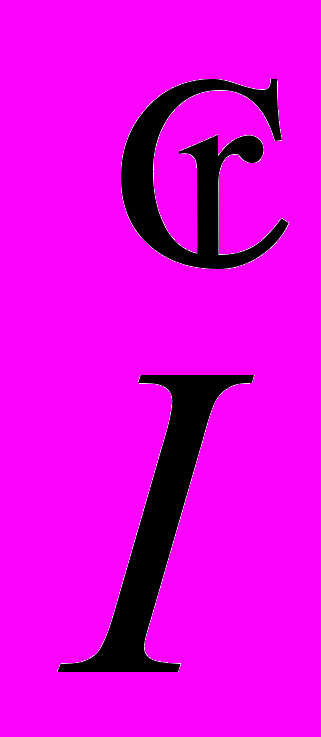 22 = -J4 = - 5 - j5 = -5 - j5 = 7,071∙ej225°
22 = -J4 = - 5 - j5 = -5 - j5 = 7,071∙ej225°4. Подставляем найденные коэффициенты в систему.
 1∙(0,05 + j0,05) +
1∙(0,05 + j0,05) +  2∙0 +
2∙0 +  3∙(-j0,1) = 0
3∙(-j0,1) = 0 1∙0 +
1∙0 +  2∙(0,1 - j0,1) +
2∙(0,1 - j0,1) +  3∙(-0,1) = -5 - j5
3∙(-0,1) = -5 - j5 1∙0 +
1∙0 +  2∙0 +
2∙0 +  3∙1 = 100
3∙1 = 1005. Для определения тока первой ветви необходимо знать потенциалы узлов "2" и "3". Потенциал узла "3" уже известен
 3 =
3 = 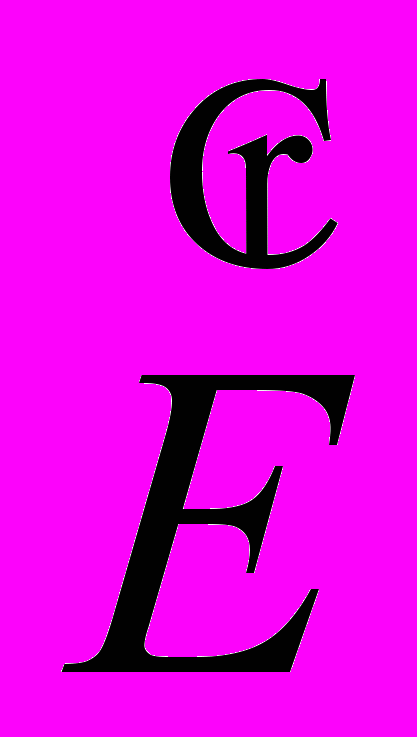 2 = 100
2 = 100Из второго уравнения находим потенциал второго узла.
 2∙(0,1 - j0,1) + 100∙(-0,1) = -5 - j5
2∙(0,1 - j0,1) + 100∙(-0,1) = -5 - j5 2∙(0,1 - j0,1) = -5 - j5 +10 = 5 – j5
2∙(0,1 - j0,1) = -5 - j5 +10 = 5 – j5 2 = (5 – j5)/(0,1 - j0,1) = 50
2 = (5 – j5)/(0,1 - j0,1) = 506. Определяем ток в первой ветви.
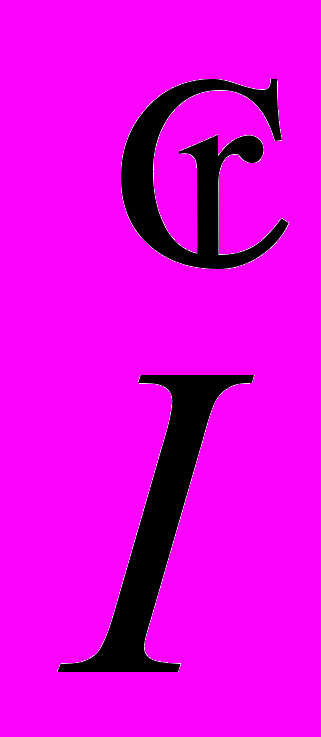 1 = (
1 = ( 2 -
2 -  3)/R1 = (50 - 100)/10 = -5 = 5∙ej180°
3)/R1 = (50 - 100)/10 = -5 = 5∙ej180°Результат решения совпадает с полученным в методе контурных токов.
3. Метод эквивалентного генератора.
1. Любой участок электрической цепи, имеющий два вывода (полюса), называется двухполюсником. Если двухполюсник содержит источники питания, он называется активным. Согласно теореме об эквивалентном генераторе любой активный двухполюсник можно заменить эквивалентным ему генератором с
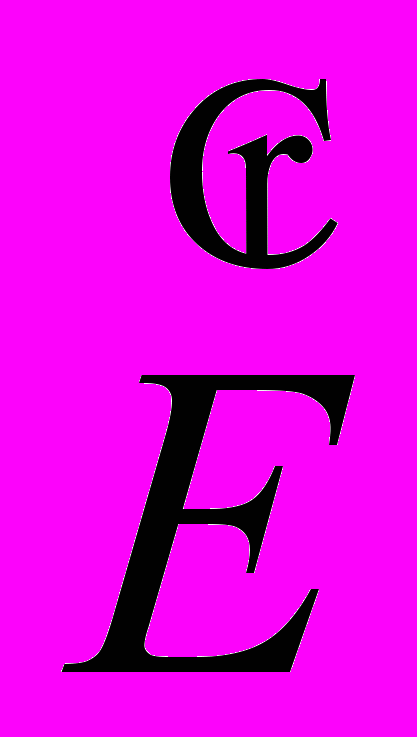 экв=
экв=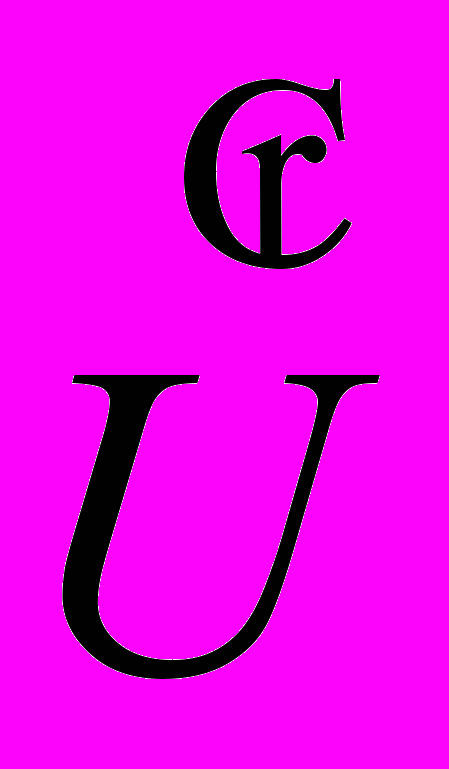 xx и Z0экв=Zвх двухполюсника. Представляем всю цепь, за исключением первой ветви, как активный двухполюсник. Создаем режим холостого хода. Так как первая ветвь теперь разомкнута, токи во всех остальных ветвях изменятся.
xx и Z0экв=Zвх двухполюсника. Представляем всю цепь, за исключением первой ветви, как активный двухполюсник. Создаем режим холостого хода. Так как первая ветвь теперь разомкнута, токи во всех остальных ветвях изменятся. 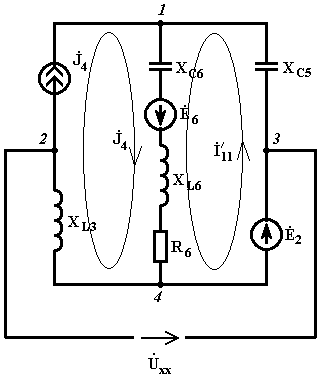
2. Для расчета токов выбираем метод контурных токов.
Из анализа схемы следует, что все необходимые параметры для нахождения напряжения холостого хода уже известны и нет необходимости выполнять расчет токов.
Используя второй закон Кирхгофа получаем:
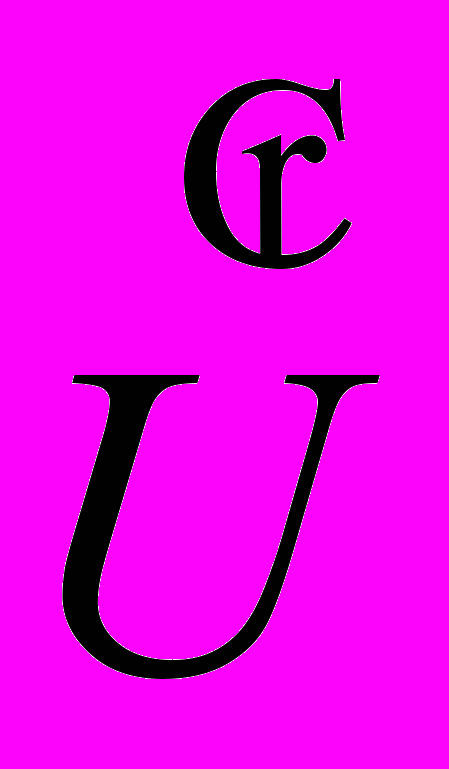 xx = -
xx = - 4∙jXL3 -
4∙jXL3 - 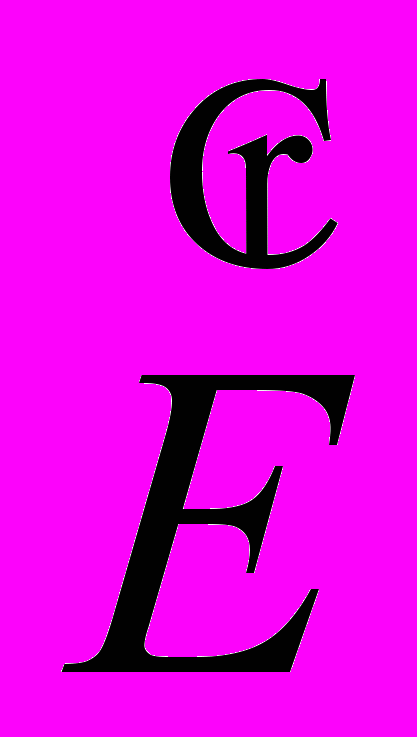 2 = (-5 - j5)∙j10 - 100 = -50 - j50 = 70,71∙ej225°
2 = (-5 - j5)∙j10 - 100 = -50 - j50 = 70,71∙ej225°3. Для определения внутреннего сопротивления двухполюсника исключим из схемы все источники электрической энергии, учитывая, что внутреннее сопротивление источника ЭДС равно нулю, а источника тока - бесконечности.
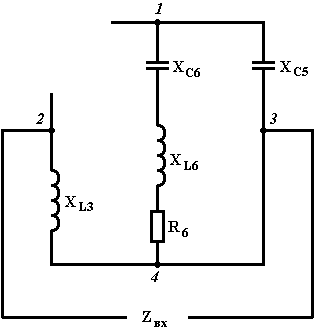
Находим входное сопротивление.
Так как участок "4-3" закорочен, получаем
Zвх = jXL3 = j10
4. Определяем ток первой ветви по закону Ома.
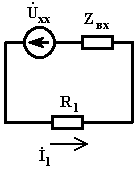
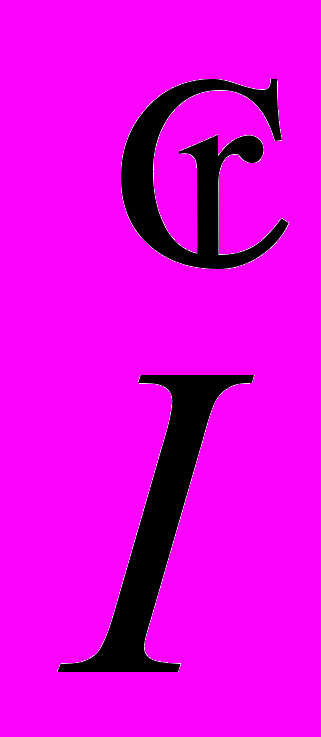 1 =
1 = 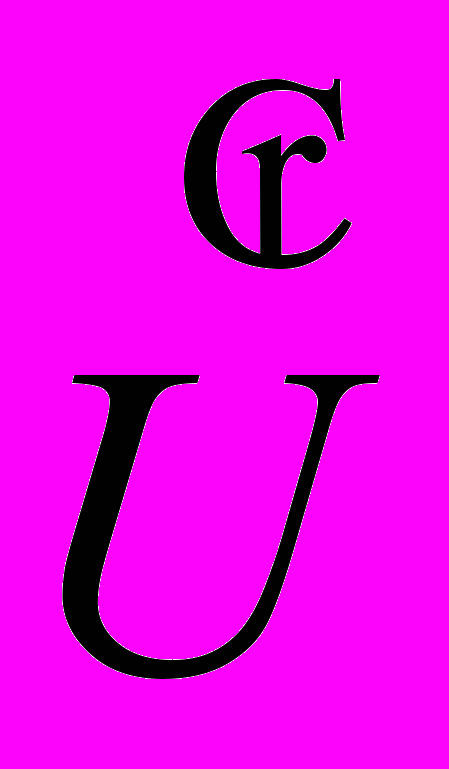 xx/(Zвх+ R1) = (-50 - j50)/(j10 + 10) = -5 = 5∙ej180° [А]
xx/(Zвх+ R1) = (-50 - j50)/(j10 + 10) = -5 = 5∙ej180° [А]Результат совпадает с полученным ранее. Расчет выполнен верно!
