Isbn 978-5-7262-1375 нейроинформатика 2011
| Вид материала | Документы |
СодержаниеКлючевые слова Постановка и редукция задачи Уравнения для внеклеточных потенциалов Результаты вычислений |
- Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.
- Isbn 978-5-7262-1375 нейроинформатика 2011, 127.94kb.
- Isbn 978-5-7262-1375 нейроинформатика 2011, 105.62kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 136.96kb.
- Isbn 978-5-7262-1376 нейроинформатика 2011, 103.58kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 136.25kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 143.59kb.
- Isbn 978-5-7262-1376 нейроинформатика 2011, 133.04kb.
ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1
А.Н. ПОКРОВСКИЙ
Санкт-Петербургский государственный университет
anpokr@petrodvorets.spb.ru
ВОЗМОЖНОСТЬ ВОССТАНОВЛЕНИЯ
СИНАПТИЧЕСКИХ ТОКОВ ПО ВЫЗВАННЫМ ПОТЕНЦИАЛАМ КОРЫ МОЗГА
Используется простая линейная аппроксимация внутриклеточных и внеклеточных потенциалов только апикальных дендритов (все остальные источники игнорируются). Оценка токов через синапсы по вызванным потенциалам является некорректной задачей математической физики. Использована новая кусочно-линейная аппроксимация токов синапсов и классический метод подбора квазирешений. Рассмотрен пример выделения двух синаптических токов из классической записи вызванных потенциалов гиппокампа.
^ Ключевые слова: вызванные потенциалы, токи синапсов, нейронные сети
Введение
Регистрация вызванных потенциалов (ВП) коры мозга является одним из распространённых методов исследования механизмов нервной системы. ВП возникают при поступлении в изучаемое место коры «залпа» нервных импульсов и выделения медиатора в синапсах возбуждённых аксонов. В результате увеличения проводимости постсинаптической части клеточной мембраны появляются «синаптические токи», вызывающие изменение как внутриклеточных, так и внеклеточных потенциалов. Суммарное изменение локального внеклеточного потенциала называется «вызванным потенциалом» (ВП).
Синаптический ток одного нейрона можно зарегистрировать в режиме фиксации потенциала этого нейрона внутриклеточным электродом. Измерение синаптического тока сразу всех нейронов в месте введения электрода невозможно. Такой суммарный ток будет суперпозицией токов синапсов разных типов, возникающих в разное время после стимуляции.
Синаптические токи при регистрации вызванных потенциалов интересны потому, что они являются непосредственным результатом активации синапсов нервными импульсами, в то время как при генерации ВП значительную роль играют и пассивные (ёмкостные и омические) токи дендритов, существенно затрудняющие интерпретацию ВП. Но, хотя суммарные синаптические токи непосредственно измерить нельзя, можно попытаться вычислить их по измеренным ВП. Эта возможность и является темой данной работы.
Данная работа является развитием исследований [1-4].
^ Постановка и редукция задачи
В первом приближении желательно использовать максимально возможную редукцию этой грандиозной по объёму задачи. ВП обычно измеряются многоканальным электродом с контактами, расположенными на равных расстояниях вдоль электрода. Этот электрод вводится поперёк поверхности коры в точке поверхности, в которой регистрируется максимум вызванного потенциала на поверхности коры. Вообще говоря, измеряемые ВП и вычисляемые токи являются функциями четырёх переменных: трёх координат и времени. С целью уменьшения размерности задачи, во-первых, будем рассматривать модель плоской коры, однородной по плоскости (x,y), и предполагать, что потенциалы и токи не зависят от координат (x,y). Вблизи электрода это приблизительно так, а влияние удалённых участков невелико и им можно пренебречь.
Во-вторых, ограничимся вычислением ВП только апикальных дендритов пирамидных клеток, игнорируя внеклеточные потенциалы всех остальных дендритов и остальных клеток коры. Это допущение можно оправдать тем, что апикальные дендриты нашей модели параллельны друг другу и их внеклеточные ВП складываются, а остальные дендриты направлены случайно и их внеклеточные ВП в значительной степени вычитаются и «гасят» друг друга.
В третьих, будем считать апикальные дендриты бесконечными цилиндрами одинакового диаметра с осями, параллельными оси z и распределёнными равномерно на плоскости (x,y). Синаптические проводимости и токи отличны от нуля только в слое коры и отсутствуют вне этого слоя.
В четвертых, будем считать, что проводимости и токи синапсов сосредоточены в тех же точках по глубине коры, что и кончики электродов, измеряющие потенциалы.
Наконец, будем считать клеточную мембрану апикальных дендритов невозбудимой, имеющей постоянную проводимость.
^ Уравнения для внеклеточных потенциалов
В основе используемых ниже уравнений лежат известные уравнения Ходжкина-Хаксли. Описанные выше допущения позволяют упростить уравнения Ходжкина-Хаксли. В результате редукции для внеклеточного потенциала φ получаем одно линейное дифференциальное уравнение параболического типа с постоянными коэффициентами. Это уравнение имеет в правой части синаптические токи I(z, t). В экспериментах с использованием внеклеточных электродов измеряются только внеклеточные потенциалы φ. Заменой переменных можно перейти к безразмерным переменным времени t и глубины z; однако при такой замене ток I(z, t) приобретет размерность потенциала. Уравнение приобретёт вид:
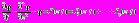 (1)
(1)Фундаментальное решение дифференциального уравнения (1) хорошо известно и вычисление потенциала при известном токе I(z,t) не представляет затруднений. Однако обратная задача (вычисление I(z,t) при известном потенциале) является неустойчивой. Наиболее традиционный путь решения обратной задачи состоит в подборе решений, для чего необходимо найти удачный способ аппроксимации тока I(z,t).
Аппроксимация токов синапсов
Используется простейшая кусочно-линейная аппроксимация синаптических токов, содержащая два линейных участка. Форма токов одного источника предполагалась одинаковой на всех уровнях отведения, отличались только амплитуды. Поскольку такая форма токов является лишь приближением к экспериментально измеряемой форме токов, результаты вычислений следует называть квазирешением обратной к (1) задаче.
На рис. 1 представлен классический пример регистрации синаптических токов в нервной клетке при фиксации внутриклеточного потенциала; обе записи сделаны в одном и том же нейроне при поступлении залпов импульсов от тормозящих и от возбуждающих аксонов. Форма возбуждающих и тормозящих токов практически одинакова, хотя они значительно отличаются по амплитуде. Очевидно также, что эти кривые достаточно хорошо аппроксимируются треугольниками.
Интересно отметить, что ни авторы [5], ни Дж. Экклс, поместивший эти кривые в разные главы своей книги [6], не заметили сходства формы этих токов, вызванных разными медиаторами.
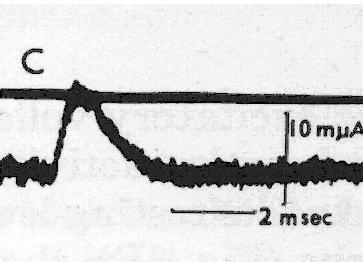
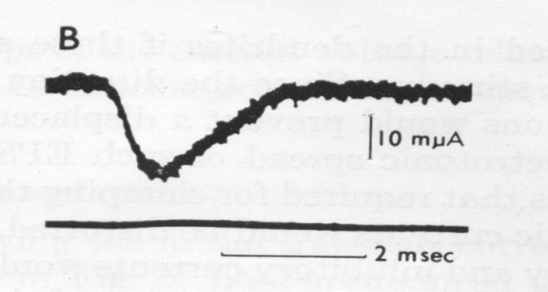
Рис. 1. Токи синапсов из статьи [5]
Подбор параметров
Токи синапсов в модели заменяются кусочно-линейными функциями (треугольниками), одинаковой формы и с одинаковой латентностью на любом уровне по глубине коры, но с разными амплитудами. Кроме латентности и амплитуд, задаются значения ещё нескольких параметров, прежде всего константа времени разряда мембраны дендрита. После этого вычисляются электрические потенциалы заданной системы токов, и вычисленные потенциалы (как функции времени) вычитаются из измеренных. Полученная система кривых оценивалась интуитивно, и затем в набор констант вносились исправления и вычисления повторялись.
Вследствие большого числа подбираемых параметров процедура подбора длилась долго. Сначала были подобраны тормозящие токи и потенциалы (на рис. 2 тормозные потенциалы направлены вниз). Затем подбирались токи возбуждающих синапсов. Оказалось, что возбуждающих импульсов было четыре («пачка» импульсов), с токами значительно меньшей величины, чем тормозящие.
^ Результаты вычислений
Вычисления производились в системе MathCAD. Использовалась возможность зрительного контроля вычислений на каждом шаге вычислений, что было существенным при не полностью формализованном алгоритме вычислений. В результате удалось подобрать синаптические токи для самого большого (тормозящего) колебания потенциала, отмеченного ещё авторами работы [7].
Кроме этого, удалось проанализировать возбуждающий потенциал в средних слоях коры, следующий непосредственно за тормозящим. Оказалось, что это колебание потенциала создано «пачкой» из четырёх возбуждающих импульсов тока примерно одинаковой величины. Амплитуда каждого из возбуждающих импульсов тока значительно меньше, чем амплитуда тормозящего, но суммарный сдвиг потенциала почти соизмерим с тормозящим.
На рис. 2 слева представлена запись вызванных потенциалов с 16 уровней коры (поле CA3 гиппокампа). Авторы [7] обратили внимание на большое колебание потенциала (примерно с 6-й по 15-ю миллисекунду) в средних слоях коры. После вычитания тормозящего потенциала осталось колебание возбуждающего потенциала, которое также было вычтено. На рис. 2 справа представлен оставшиеся после этих вычитаний потенциалы. На рис. 3 – вычисленные токи синапсов.
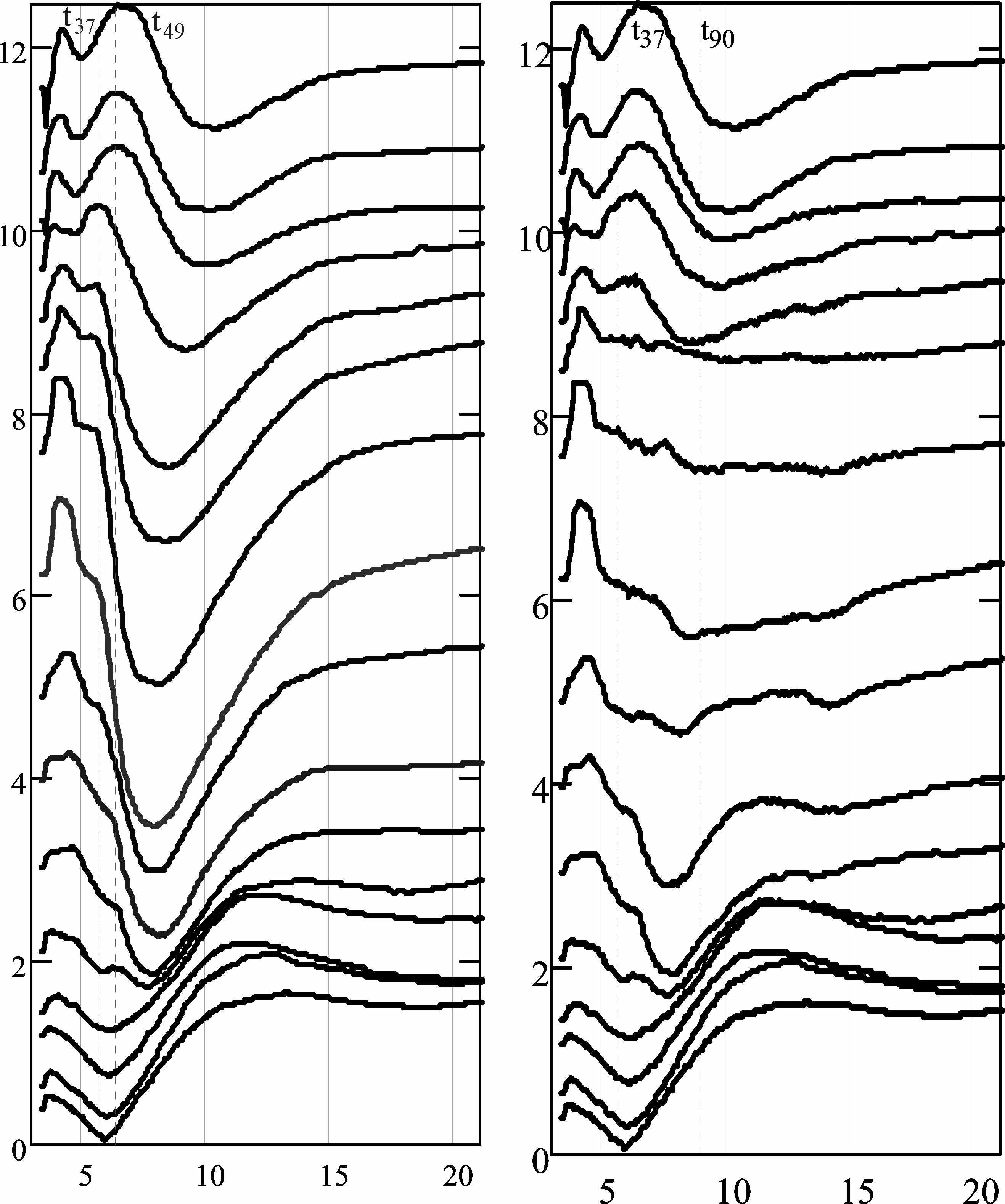
Рис. 2. Слева – вызванные потенциалы из [7]. Справа – те же потенциалы, из которых вычтены потенциалы подобранных токов двух типов синапсов. По оси абсцисс – время в миллисекундах, по осям ординат – потенциал в милливольтах
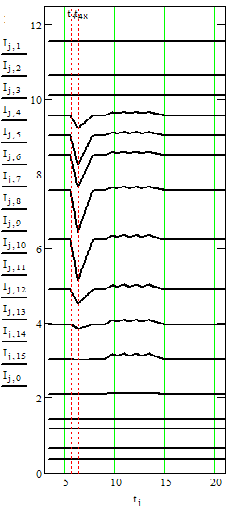
Рис. 3. Подобранные синаптические токи. По оси абсцисс – время в миллисекундах, по оси ординат – потенциалы в милливольтах
Выводы
Предложен и реализован алгоритм подбора компонентов синаптических токов по записи вызванных потенциалов. Алгоритм нуждается в дальнейшей разработке для использования на компьютерах. Основная проблема состоит в том, что из-за большой размерности задачи полный перебор вариантов практически невозможен, и необходимо пути более эффективного решения задачи
Путь решения задачи анализа вызванных потенциалов найден не для всех структур коры. Известно, что в некоторых частях коры мозга существуют не только синаптические связи между нейронами, но и электрические, в том числе и поры между соседними нейронами. Одна из самых актуальных задач состоит в разработке модели вызванных потенциалов в таких структурах.
Список литературы
Покровский А.Н. Латентные периоды компонентов вызванных потенциалов // Доклады РАН, 2002. Т. 384, № 5. С. 708–711.
Покровский А.Н. Обратная задача анализа внеклеточных потенциалов в слое параллельных дендритов // «Проблемы нейрокибернетики» (материалы 14-й Международной конференции по нейрокибернетике). Ростов-на-Дону, 2005. Т. 2. С. 136–139.
Покровский А.Н. Обратная задача моделирования внеклеточных потенциалов коры мозга // Системы управления и информационные технологии, 2006. №1(23). С. 94–98.
Покровский А.Н., Федоров А.С. Анализ записей вызванных потенциалов коры мозга // Нейроинформатика, её приложения и анализ данных. Материалы XVI Всероссийского семинара. Красноярск, 2008. С. 106–109.
Araki T., Terzuolo C.A. J. // Neurophysiol. 1962, v. 25, № 6. P. 772–789. Fig. 7, 8.
Экклс Дх. Физиология синапсов. М.: Мир, 1966.
Andersen P., Eccles J.C., Loyning Y. // Nature (Lond.), 1963. V. 198. P. 541–542.
Данная работа выполнена при частичной поддержке РФФИ, проект № 09-01-00473-а.
УДК 004.032.26(06) Нейронные сети
