Isbn 978-5-7262-1375 нейроинформатика 2011
| Вид материала | Документы |
- Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.
- Isbn 978-5-7262-1375 нейроинформатика 2011, 105.62kb.
- Isbn 978-5-7262-1375 нейроинформатика 2011, 79.42kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 136.96kb.
- Isbn 978-5-7262-1376 нейроинформатика 2011, 103.58kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 136.25kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 143.59kb.
- Isbn 978-5-7262-1376 нейроинформатика 2011, 133.04kb.
ISBN 978-5-7262-1375-0. НЕЙРОИНФОРМАТИКА – 2011. Часть 1
А.П. КАРПЕНКО, Д.А. МООР, Д.Т. МУХЛИСУЛЛИНА
Московский государственный технический университет им. Н.Э. Баумана
dmitry_moor@mail.ru
НЕЙРОСЕТЕВАЯ, НЕЧЕТКАЯ И НЕЙРО-НЕЧЕТКАЯ
АППРОКСИМАЦИЯ В ЗАДАЧЕ
МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Рассматривается прямой адаптивный метод многокритериальной оптимизации на основе аппроксимации функции предпочтения лица, принимающего решение, с помощью нейронных сетей, нечеткой логики и нейро-нечеткого вывода. Проведен сравнительный анализ этих методов при решении 2-х и 3-х критериальных тестовых задач многокритериальной оптимизации.
Ключевые слова: многокритериальная оптимизация, нейронные сети, нечеткая логика, ANFIS
Введение
Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач).
В МКО-задаче предполагается, что задана вектор-функция
 компоненты которой называются частными критериями оптимальности. Эта функция определена на множестве допустимых значений (множестве альтернатив)
компоненты которой называются частными критериями оптимальности. Эта функция определена на множестве допустимых значений (множестве альтернатив)  вектора варьируемых параметров X. Лицу, принимающему решения (ЛПР), желательно найти такое решение на множестве
вектора варьируемых параметров X. Лицу, принимающему решения (ЛПР), желательно найти такое решение на множестве  , которое минимизировало бы (для определенности) все компоненты вектор-функции
, которое минимизировало бы (для определенности) все компоненты вектор-функции  .
. Прямой адаптивный метод решения МКО-задачи, который рассматривается в данной работе, основан на предположении существования функции предпочтения (ФП) лица, принимающего решения
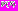 , определенной на множестве
, определенной на множестве 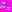 и выполняющей его отображение во множество действительных чисел R, т.е.
и выполняющей его отображение во множество действительных чисел R, т.е. 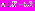 .
.При этом задача многокритериальной оптимизации сводится к задаче выбора такого вектора
 , что
, что 
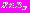
Предполагается, что при предъявлении ЛПР вектора параметров X, а также соответствующих значений всех частных критериев оптимальности
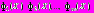 ЛПР может оценить соответствующее значение ФП
ЛПР может оценить соответствующее значение ФП 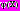 [1].
[1].В работе [2] предложен класс прямых адаптивных методов решения МКО-задачи, основанных на аппроксимации функции
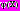 . В данной работе рассматриваются и сравниваются следующие методы этого класса:
. В данной работе рассматриваются и сравниваются следующие методы этого класса:- метод, основанный на аппроксимации ФП ЛПР с помощью 11 многослойных персептронных сетей (MLP-сети), а также с помощью нейронных сетей с радиально-базисными функциями (RBF-сети);
- метод, в основе которого лежит аппроксимация ФП ЛПР посредством аппарата нечеткой логики;
- метод, основанный на аппроксимации ФП ЛПР с помощью аппарата нейро-нечеткого вывода.
Постановка задачи многокритериальной оптимизации
Пусть
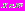 – вектор параметров задачи (вектор варьируемых параметров), где
– вектор параметров задачи (вектор варьируемых параметров), где  – n-мерное арифметическое пространство (пространство параметров). Множеством допустимых значений вектора параметров X является ограниченное замкнутое множество
– n-мерное арифметическое пространство (пространство параметров). Множеством допустимых значений вектора параметров X является ограниченное замкнутое множество  где
где  – «технологический» параллелепипед допустимых значений вектора параметров,
– «технологический» параллелепипед допустимых значений вектора параметров,
множество
 формируют ограничивающие функции
формируют ограничивающие функции 
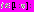
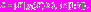
Векторный критерий оптимальности
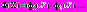
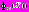 со значениями в пространстве
со значениями в пространстве  определен в параллелепипеде П. ЛПР стремится минимизировать на множестве
определен в параллелепипеде П. ЛПР стремится минимизировать на множестве  каждый из частных критериев оптимальности
каждый из частных критериев оптимальности  что условно записывается в виде
что условно записывается в виде 
 (1)
(1) где
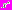 – искомое решение МКО-задачи.
– искомое решение МКО-задачи.Введем следующие обозначения:
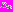 – критериальное множество (множество достижимости) задачи, т.е. множество, в которое векторный критерий оптимальности отображает множество
– критериальное множество (множество достижимости) задачи, т.е. множество, в которое векторный критерий оптимальности отображает множество 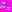 ;
; 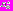 – фронт Парето задачи,
– фронт Парето задачи, 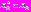 ;
;  – множество Парето. Если
– множество Парето. Если  то будем говорить, что вектор X – эффективный по Парето вектор [1]. Положим, что частные критерии оптимальности тем или иным образом нормализованы [2].
то будем говорить, что вектор X – эффективный по Парето вектор [1]. Положим, что частные критерии оптимальности тем или иным образом нормализованы [2]. Рассмотрим решение задачи (1) методом скалярной свертки. Способ свертки не фиксируется. Обозначим операцию свертки
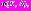 где
где 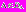 – вектор весовых множителей,
– вектор весовых множителей, 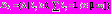 – множество допустимых значений этого вектора.
– множество допустимых значений этого вектора.При каждом фиксированном векторе
 метод скалярной свертки сводит решение задачи (1) к решению однокритериальной задачи глобальной условной оптимизации
метод скалярной свертки сводит решение задачи (1) к решению однокритериальной задачи глобальной условной оптимизации
 . (2)
. (2)В силу ограниченности и замкнутости множества
 решение этой задачи существует.
решение этой задачи существует. Если при каждом
 решение задачи (2) единственно, то это решение ставит в соответствие каждому из допустимых векторов
решение задачи (2) единственно, то это решение ставит в соответствие каждому из допустимых векторов  единственный вектор
единственный вектор 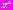 и соответствующие значения частных критериев оптимальности
и соответствующие значения частных критериев оптимальности 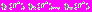 Данное обстоятельство позволяет полагать, что в этом случае ФП ЛПР определена не на множестве
Данное обстоятельство позволяет полагать, что в этом случае ФП ЛПР определена не на множестве 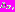 а на множестве
а на множестве  :
: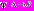 .
.В результате МКО-задача сводится к задаче выбора вектора
 такого, что
такого, что  ,
,  . (3)
. (3)Поскольку обычно
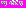 , переход от задачи (1) к задаче (3) важен с точки зрения уменьшения вычислительных затрат.
, переход от задачи (1) к задаче (3) важен с точки зрения уменьшения вычислительных затрат. Величину будем считать лингвистической переменной со значениями, меняющимися от «Очень-очень плохо» до «Отлично» [4]. Обозначим
 – ядро нечеткой переменной , принимающее значения от 1 до 9.
– ядро нечеткой переменной , принимающее значения от 1 до 9. В результате МКО-задача сводится к задаче отыскания вектора
 обеспечивающего максимальное значение дискретной функции
обеспечивающего максимальное значение дискретной функции 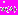 :
: ,
,  . (4)
. (4)Таким образом, задача сводится к аппроксимации ФП ЛПР.
Метод решения задачи
Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов.
Этап «разгона» метода. МКО-система некоторым образом (например, случайно) последовательно генерирует k векторов
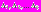 и для каждого из этих векторов выполняет следующие действия:
и для каждого из этих векторов выполняет следующие действия:- решает однокритериальную задачу (ОКО-задачу)
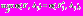

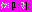 (5)
(5)2) предъявляет ЛПР найденное решение
 а также соответствующие значение всех частных критериев оптимальности
а также соответствующие значение всех частных критериев оптимальности 
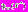 ;
;3) ЛПР оценивает эти данные и вводит в МКО-систему соответствующее значение своей ФП
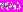
Первый этап. На основе всех имеющихся в МКО-системе значений
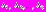 вектора
вектора  и соответствующих оценок ФП
и соответствующих оценок ФП 
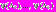 МКО-система выполняет следующие действия:
МКО-система выполняет следующие действия:1) строит функцию
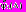 аппроксимирующую функцию
аппроксимирующую функцию 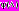 в окрестности точек
в окрестности точек  ;
;2) отыскивает максимум функции
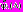 – решает ОКО-задачу
– решает ОКО-задачу 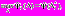
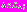 (6)
(6)3) с найденным вектором
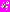 решает ОКО-задачу вида (5) – находит вектор параметров и соответствующие значения частных критериев оптимальности, а затем предъявляет их ЛПР. ЛПР оценивает указанные данные и вводит в систему соответствующее значение своей ФП
решает ОКО-задачу вида (5) – находит вектор параметров и соответствующие значения частных критериев оптимальности, а затем предъявляет их ЛПР. ЛПР оценивает указанные данные и вводит в систему соответствующее значение своей ФП 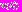 .
.Второй этап. На основе всех имеющихся в системе значений
 вектора
вектора  и соответствующих оценок ФП
и соответствующих оценок ФП  МКО-система выполняет аппроксимацию функции
МКО-система выполняет аппроксимацию функции  в окрестности точек
в окрестности точек  – строит функцию
– строит функцию  и т.д. по схеме первого этапа до тех пор, пока ЛПР не примет решение о прекращении вычислений.
и т.д. по схеме первого этапа до тех пор, пока ЛПР не примет решение о прекращении вычислений.Особенности нейросетевой аппроксимации ФП ЛПР
Аппроксимация ФП ЛПР нейронными сетями имеет в данном случае ту особенность, что процесс обучения нейронных сетей происходит в условиях малой обучающей выборки. Это обстоятельство обусловлено тем, что количество «разгонных» итераций не должно быть слишком большим, иначе ЛПР может прекратить процесс вычислений, не получив окончательного решения. Как следствие, для аппроксимации ФП ЛПР в работе используются только двухслойные MLP и RBF нейронные сети.
Поскольку на компоненты вектора весовых множителей
 наложено ограничение
наложено ограничение 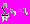 один из весовых множителей (пусть это будет множитель
один из весовых множителей (пусть это будет множитель  можно выразить через остальные множители:
можно выразить через остальные множители: 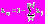 . Вследствие этого, в качестве входов нейронных сетей рассматриваются только компоненты
. Вследствие этого, в качестве входов нейронных сетей рассматриваются только компоненты  , вектора
, вектора  .
.ЛПР в процессе решения МКО–задачи может переоценивать результаты предыдущих итераций, указанные им оценки могут быть противоречивы.
Особенности аппроксимации ФП ЛПР с помощью аппарата
нечеткой логики
Входами системы нечеткого вывода в данном случае являются значения весов частных критериев оптимальности – нечеткие термы
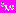 ,
, 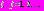
 . Выходной переменной системы нечеткого вывода является лингвистическая переменная , ядро которой
. Выходной переменной системы нечеткого вывода является лингвистическая переменная , ядро которой  принимает значения 1, 2,…, 9.
принимает значения 1, 2,…, 9.Взаимосвязь между входными и выходными переменными описывается нечеткими правилами вида
ЕСЛИ <значения входных переменных>,
ТО <значение выходной переменной>
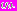
Здесь
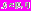 – коэффициенты определенности (веса нечетких правил).
– коэффициенты определенности (веса нечетких правил).Совокупность значений указанных нечетких входных переменных, выходных лингвистических переменных, а также правил нечетких продукций образуют нечеткую базу знаний.
Используется схема нечеткого вывода Мамдани, которая выполняется за два шага [6].
Шаг 1. Положим, что выполнено N экспериментов по определению значений лингвистической переменной . Пусть в
 этих экспериментов переменная приняла значение
этих экспериментов переменная приняла значение 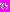 , в
, в  экспериментах – значение
экспериментах – значение 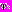 и т.д. до
и т.д. до  и
и  . Соответствующие входные векторы
. Соответствующие входные векторы  обозначим
обозначим  ,
,  ,
,  .
.Матрицу знаний
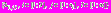 представим в виде
представим в виде 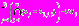 ,
, 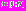 .
.Шаг 2. Тонкая настройка модели
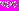 (параметрическая идентификация модели) осуществляется путем подбора следующих параметров: полуширина a функций принадлежности входных переменных
(параметрическая идентификация модели) осуществляется путем подбора следующих параметров: полуширина a функций принадлежности входных переменных  ; полуширина
; полуширина  функций принадлежности выходных переменных
функций принадлежности выходных переменных  ; величина δ, определяющая закон изменения весовых множителей правил. Область допустимых значений указанных параметров представляет собой параллелепипед
; величина δ, определяющая закон изменения весовых множителей правил. Область допустимых значений указанных параметров представляет собой параллелепипед  , а критерий оптимальности имеет вид
, а критерий оптимальности имеет вид
 ,
,где
 – результат нечеткого логического вывода Мамдани в точке
– результат нечеткого логического вывода Мамдани в точке 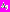 .
.Таким образом, формально задача параметрической идентификации формулируется в виде следующей задачи глобальной многомерной условной оптимизации
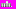
 ,
,  . (7)
. (7) Особенности аппроксимации ФП ЛПР с помощью аппарата
нейро-нечеткого вывода
Используется адаптивная нейро-нечеткая система вывода ANFIS, функционально эквивалентная системе нечеткого вывода Сугено. Вывод осуществляется за два шага, которые по сути своей аналогичны шагам, рассмотренным в предыдущем разделе. Особенностью метода является наличие этапа тонкой настройки ФП в предпосылках и заключениях правил, этот этап проводится с использованием алгоритмов обучения нейронных сетей.
Система ANFIS реализуется в виде нейроподобной структуры, состоящей из пяти слоев (рис. 1). Для обучения сети был применен гибридный градиентный метод.

Рис. 1. Структура нейро-нечеткой сети ANFIS
По мере приобретения новых знаний меняется топология нечеткой нейронной сети, для чего используется процедура, предложенная в работе [3].
Исследование эффективности методов
Исследование эффективности выполнено для следующих тестовых задач.
Двухкритериальная задача 1, имеющая выпуклый фронт Парето:
 ;
;  ;
;  .
.Двухкритериальная задача 2 (невыпуклый многосвязный фронт Парето):

 ;
; ;
;  .
.Трехкритериальная задача 3 (выпуклый фронт Парето):
 ;
;  ;
; ;
;  .
.Для всех трех задач полагалось, что число k «разгонных» значений вектора
 равно трем (k=3).
равно трем (k=3).Исследование вышеперечисленных МКО-задач проводилось на MLP-сетях с тремя (MLP3), пятью (MLP5), семью (MLP7) и девятью (MLP9) нейронами в скрытом слое и на RBF-сети (RBF), а также с использованием системы нечеткого вывода Мамдани (Fuzzy) и с использованием нейро-нечеткого логического вывода ANFIS (ANFIS).
Результаты исследования сведены в таблицу 1. Результаты более широкого исследования приведены в работах [4], [5], [6].
Таблица 1
Результаты исследования эффективности метода
| | МКО-задача 1 | МКО-задача 2 | МКО-задача 3 |
| MLP3 | 9 | 6 | 7 |
| MLP5 | 5 | 5 | 13 |
| MLP7 | 10 | 7 | 13 |
| MLP9 | 9 | 5 | 8 |
| RBF | 5 | 6 | 5 |
| Fuzzy | 8 | 11 | 14 |
| ANFIS | 5 | 7 | 9 |
Исследование показало, что, хотя использование всех рассматриваемых технологий аппроксимации ФП ЛПР обеспечивает получение оптимального решения, методы, основанные на MLP сетях с пятью и девятью нейронами в скрытом слое, а также RBF-сети и системе ANFIS позволяют находить лучшее решение за наименьшее количество итераций.
Вид функции
 после 7 итераций решения МКО-задачи 2 с использованием аппарата нейро-нечеткого вывода показан на рис. 2.
после 7 итераций решения МКО-задачи 2 с использованием аппарата нейро-нечеткого вывода показан на рис. 2. 
Рис. 2. Аппроксимация ФП ЛПР для МКО-задачи 2: ANFIS; 7-я итерация
Выводы
Разработан адаптивный метод решения МКО-задачи, основанный на аппроксимации функции предпочтений ЛПР с помощью нейронных сетей, аппарата нечеткой логики, а также с использованием нейро-нечеткого вывода. Проведен сравнительный анализ эффективности всех трех методов аппроксимации на тестовых двух- и трехкритериальных задачах. Исследование показало перспективность развития всех указанных методов аппроксимации.
В развитии работы предполагается провести апробацию метода на практической МКО-задаче. Кроме того, планируется исследовать эффективность предложенных методов для решения МКО-задач в случае, когда решение принимается не ЛПР, а группой лиц (ГПР).
Список литературы
1. Лотов А.В. Введение в экономико-математическое моделирование. – М.: Наука, 1984. 392 с.
2. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации, использующие аппроксимацию функции предпочтений лица, принимающего решения // Электронное научно-техническое издание: наука и образование. 2008. №8. (.edu.ru/doc/101804.php).
3. Штойер Р. Многокритериальная оптимизация. Теория, вычисления и приложения. – М.: Радио и связь, 1992. 504 с.
4. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. – М.: Горячая линия – Телеком, 2002. 382 с.
5. Ларичев О.И. Теория и методы принятия решений. – М.: Университетская книга, Логос, 2006. 392 с.
6. Карпенко А.П., Федорук В.Г. Аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации. 3. Методы на основе нейронных сетей и нечеткой логики // Электронное научно-техническое издание: наука и образование. 2008. №4. (ссылка скрыта).
7. Карпенко А.П. Нейросетевая аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации // Информационные технологии. 2010 (в печати).
8. Карпенко А.П., Моор Д.А., Мухлисуллина Д.Т. Многокритериальная оптимизация но основе нечеткой аппроксимации функции предпочтений лица, принимающего решения // Наука и образование: электронное научно-техническое издание. 2010. 1 (ссылка скрыта)
УДК 004.032.26(06) Нейронные сети
