Isbn 978-5-7262-1226 нейроинформатика 2010

Вид материала

Документы

Содержание Налогового и финансового контроля Алгоритм I обеспечения состоятельности задачи регуляризации Алгоритм II построения подходящей числовой меры оценки погрешности данных на основе байесовского подхода. Однако заметим, что при малых S, т.е. при сильных сжимающих свойствах НС-отображения Алгоритм III построения числовой меры оценки качества НСМ Пример использования байесова подхода к прогнозным оценкам. W – искомая в обратной задаче обучения матрица синаптических весов. В качестве пространства гипотез выбрано W W. Например, в случае нейросетевой аппроксимации W Результаты моделирования для объекта № 2

Подобный материал:

• Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 9.21kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 113.94kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 89.17kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 124.83kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 86.68kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 101.88kb.
• Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 127.94kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.

С.А. ГОРБАТКОВ¹, Д.В. ПОЛУПАНОВ², С.А. ФАРХИЕВА<sup>1

1</sup>Филиал Всероссийского заочного финансово-экономического института, Уфа

² Башкирский государственный университет, Уфа

¹gorbatkov.ufa@vzfei.ru, ¹sagor@ufanet.ru, ²demetrious@mail.ru, ³ok-xi@yandex.ru


ОБОБЩЕНИЕ МЕТОДА ВЛОЖЕННЫХ

МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ НА ОСНОВЕ

БАЙЕСОВСКОГО ПОДХОДА К РЕГУЛЯРИЗАЦИИ ЗАДАЧ

НЕЙРОСЕТЕВОГО МОДЕЛИРОВАНИЯ

НАЛОГОВОГО И ФИНАНСОВОГО КОНТРОЛЯ


Исследованы вопросы обеспечения состоятельности регуляризированных по принципу квазиминимизации А.Н. Тихонова обратных задач восстановления многофакторных экономических зависимостей в нейросетевом базисе. На основе байесовского подхода систематизирован и разработан в деталях метод вложенных математических моделей для нейросетевых экономических объектов с существенным искажением данных. Теоретические положения подтверждаются вычислительными экспериментами на реальных данных муниципальных образовательных учреждений при планировании фонда материального развития.


Предметом исследования в работе являются вопросы регуляризации обратных задач восстановления многофакторных нелинейных зависимостей, «зашитых» в данных, в рамках построения нейросетевых моделей (НСМ) налогового и финансового контроля. Круг приложений таких моделей весьма широк [1-3]. Как известно [4-6], рассматриваемые задачи относятся к классу задач, некорректно поставленных по Адамару. В случае ограниченного объема данных, а именно такие приложения рассматриваются авторами, необходима регуляризация обратных задач [7]. Положение усугубляется при сильном зашумлении данных (вплоть до сознательного их искажения! [1]).

В наших исследованиях по регуляризации НСМ мы основывались на принципе регуляризации по А.Н. Тихонову [4], который сводит ее к решению задачи квазиминимизации для операторного уравнения:

; (1)

, (2)

где – оператор отображения «вход-выход» НСМ в режиме обучения, т.е. обратной задачи; это оператор различных поисковых алгоритмов параметров НСМ – матрице синаптических весов W, а в прямой задаче в режиме расчета выхода при подаче новых сигналов на вход нейросети (НС). – это композиция операторов проецирования сигналов с заданными синаптическими весами с последующей нелинейной аппроксимацией с помощью активационной функции НС [8]; z – точное решение обратной задачи (1); u – наблюдаемые характеристики объекта, содержащиеся в данных; – зашумленные значения u; U – пространство зашумляемых данных; – множество практической эквивалентности, удовлетворяющее условию квазиминимизации (2); – компакт; – расстояние между элементами в пространстве U; δ – оценка погрешности данных.

Математический анализ, основанный на теореме А.Н. Тихонова [4], приводит к выводу, что выбор (2) решения из множества практической эквивалентности можно гарантировать, если потребовать принадлежности решения к тому же компакту , что и точное решение операторного уравнения (1).

В решении обратной задачи (1)-(2) участвует разнородная информация об изучаемом явлении: его НСМ , некоторые общие свойства искомого решения , оценка погрешности данных δ. Если эта информация не согласована, т.е. и задаются независимо, то может возникнуть ситуация несостоятельности задачи регуляризации (1)-(2):

. (3)

Связанная с этой ситуацией потеря устойчивости НСМ подробно анализировалась в [1, 2, 9]. Следовательно, для практической регуляризации А.Н. Тихонова по (1)-(2) необходимо разработать три алгоритма:

1. алгоритм I обеспечения состоятельности задачи регуляризации (1)-(2), исключающий ситуацию (3);
   
2. алгоритм II построения подходящей числовой меры оценки погрешности  для данных и инструмент управления этой погрешностью;
   
3. алгоритм III построения числовой меры оценки качества НСМ и инструмента управления этим качеством.
   

Отдельные предложения по алгоритмам I, II и III были сформулированы и апробированы авторами в вычислительных экспериментах в [1, 2, 9-12]. Эти предложения можно объединить под названием «метод вложенных математических моделей (ВММ) для НСМ экономических объектов с сильным зашумлением данных».

В настоящей работе метод ВММ для регуляризации обратных задач восстановления данных согласно принципу (1)-(2) систематизирован и разработан в деталях на основе байесовского подхода к сравнению моделей, развитому в [7].

Алгоритм I обеспечения состоятельности задачи регуляризации. Постулируется, что в некоторых пределах интенсивности шума и объема сильнозашумленных вектор-столбцов данных , , , где , – соответствующие значения компонента вектора входов НС X и выхода НС Y в i-м наблюдении, независимо от закона распределения шума существует непрерывная зависимость меры по (3), характеризующей качество аппроксимации в НСМ, от меры оценки погрешности данных δ

. (4)

Предлагается следующая концепция разработки методов и алгоритмов обеспечения состоятельности задач регуляризации: уменьшение числовых мер ошибок эксперимента δ и ошибок аппроксимации должно производиться взаимосвязано с использованием объективно существующей закономерности (4), причем числовая мера δ должна быть связана процедурой управления структурирования данных в аспекте улучшения качества будущего обучения НС. Управление качеством данных по мере δ предлагается осуществлять на основе вспомогательных нейросетевых субмоделей (НССМ), в которых реализуются следующие итерационные процедуры структурирования данных:

• оптимальная кластеризация;
  
• оптимальная очистка данных в образованных кластерах;
  
• «ремонт» сильнозашумленных вектор-столбцов данных с помощью НССМ.
  

Указанные процедуры, разработанные с использованием общесистемных законов энтропийного равновесия, появления дисфункций структурируемой системы и фоновой закономерности [13], описаны достаточно подробно в [1, 2, 9-12], поэтому излагать их здесь не будем.

Алгоритм II построения подходящей числовой меры оценки погрешности данных на основе байесовского подхода. Формулировке алгоритма предпошлем краткое изложение формализма байесовского подхода к сравнению моделей, развитого в [7].

Байесов подход к обучению, основанный на решении обратной задачи, более последователен и, соответственно, применим к более широкому классу моделей с большими возможностями моделирования сложных явлений. Тем более, что в общем виде эта задача решается «в одну строку» и ее решение, следующее из общих принципов теории вероятностей, было известно уже в XVIII веке. Действительно, если трактовать как выбор гипотезы, так и наблюдение данных в вероятностном смысле и записать согласно определению условных вероятностей

,

получим теорему Байеса:

. (5)

Здесь – апостериорная вероятность конкретной гипотезы h о порождении данных D, т.е. мера правдоподобия наблюдения данных в соответствии с гипотезой h; – априорная вероятность гипотезы h; – фактически наблюдаемая суммарная по всем гипотезам вероятность данных (Evidence) D.

Как видим, решение обратной задачи требует формализации наших априорных (prior) предположений о степени вероятности той или иной гипотезы. Подобного рода ограничение на множество гипотез, в котором ищется решение, в теории обратных задач называют регуляризацией. Необходимость ее связана с конечным объемом эмпирических данных. Если мы не будем ограничены в средствах, то всегда сможем подобрать гипотезу, идеально объясняющую имеющиеся данные, но с плохими способностями к обобщению: . Иными словами, такие гипотезы (называемые по латыни ad hoc) чрезвычайно чувствительны к конкретному набору обучающих данных. Чувствительность к данным есть индикатор того, что задача обучения по своей природе некорректна, и как всякая некорректная, обратная задача требует регуляризации. В ограниченном классе гипотез чрезмерную чувствительность решения к обучающей выборке можно преодолеть.

Выбор метода регуляризации, то есть класса гипотез, в свою очередь, является мета-гипотезой H более высокого порядка, которые в теории машинного обучения принято называть моделями: . Так, в задаче интерполяции функций модель фиксирует выбранный метод параметризации функций, например, персептрон с заданной топологией связей или сплайны определенного порядка. Конкретные значения подгоночных параметров соответствуют гипотезам. Гипотезы всегда выбираются в рамках той или иной модели и, с этой точки зрения, все вероятности в формуле Байеса зависят от H:

. (6)

Фундаментальный характер теоремы Байеса позволяет в едином ключе сравнивать между собой не только гипотезы, но и различные модели регуляризации. Тем самым, байесовский подход позволяет расширить рамки традиционной теории регуляризации, не предполагающей сравнение между собой регуляризирующих функционалов .

Главный результат из работы [7], который «эксплуатируется» авторами при разработке алгоритма II формулируется так. Модель порождения данных в байесовской трактовке представлена ансамблем гипотез. Обучение увеличивает наше знание относительно такой модели. Ему предшествует некий априорный ансамбль гипотез, а результатом является более компактный апостериорный ансамбль гипотез. Предсказания модели подразумевают усреднение по этому ансамблю. При этом, качество предсказаний ансамбля выше, чем качество предсказания его наилучшей гипотезы. Оптимальному апостериорному ансамблю соответствует максимальная вероятность (знаменатель формулы Байеса).

В общем виде алгоритм II, предлагаемый в настоящей работе, можно сформулировать следующим образом: в качестве числовой меры δ погрешности данных выбирается обобщенный (векторный) мультипликативный критерий Ф, оцениваемый согласно алгоритму I в НССМ путем осреднения в ансамбле НС и определенный на обучающем множестве данных :

, (7)

где  – ошибка обобщения НСМ, которая имеет смысл относительной нормы ошибок аппроксимации на тестовом множестве наблюдений, не используемых при обучении НСМ; – мера сжимающих свойств НСМ (аналог константы Липшица связи «вход-выход» НС); – мера отклонения коэффициента детерминации от его идеального значения, равного 1 [2]. Ошибка обобщения E характеризует прогностические свойства НС: чем меньше E, тем ближе расчетные значения к экспериментальным y на новых наблюдениях. Частный критерий S характеризует устойчивость НСМ к вариациям независимых переменных x: чем меньше S, тем меньше «разбегание» траектории на новых наблюдениях после обучения НС. Однако заметим, что при малых S, т.е. при сильных сжимающих свойствах НС-отображения (1), в режиме обучения НС, т.е. в обратной задаче поиска параметров W НСМ оператор ведет себя как вполне непрерывный (компактный) оператор [7], что является индикатором некорректности обратной задачи. Критерий R характеризует качество аппроксимации «зашитых» в данных истинной зависимости , т.е. гиперповерхности с помощью нейросетевого отображения .

Таким образом, обобщенный критерий качества НСМ Ф оценивает как точностные и прогностические свойства НС, так и ее устойчивость по вариации данных.

Осреднение в ансамбле гипотез проводится как вычисление среднего арифметического

, (8)

где Q – число вспомогательных НССМ в ансамбле.

Алгоритм III построения числовой меры оценки качества НСМ и инструмента управления этим качеством. Конструирование меры осуществлено на основе байесовского подхода (5)-(6), т.е. использовано усреднение оценки качества аппроксимации в НСМ на ансамбле гипотез о порождении данных, аналогично алгоритму II предобработки данных. В качестве меры взято среднее значение вероятности получения в НСМ «плохих» точек, в которых относительная ошибка расчета в сети превышает заданный экспертно уровень :

(9)

(10)

где – число «плохих» точек; – общее число точек для q-й НСМ в ансамбле; Q – число сетей в ансамбле; – тестовое множество примеров в данных рабочей НСМ (после предобработки данных).

Пример использования байесова подхода к прогнозным оценкам. Рассмотрим задачу ранжирования муниципальных образовательных учреждений при планировании фонда материального развития из [2]. Постановка задачи: входы описываются n-мерным вектором X, а выход – скалярным агрегированным показателем , характеризующим эффективность работы муниципального образования. W – искомая в обратной задаче обучения матрица синаптических весов.

В качестве пространства гипотез выбрано W-параметрическое семейство функций с заданными ограничениями на значения ее параметров W. Например, в случае нейросетевой аппроксимации W есть множество настроечных синаптических весов.

В качестве мета-гипотезы H принята парадигма НС многослойный персептрон с алгоритмом обучения типа обратного распространения ошибки. В пространстве гипотез варьировались архитектура НС и вид активационных функций в скрытых слоях:

• гипотеза – НС с одним скрытым слоем с сигмоидной функцией активации:
  

; (11)

• гипотеза – НС с двумя скрытыми слоями с функцией активации (11) в обоих слоях;
  
• гипотеза – НС с двумя скрытыми слоями с функцией активации (11) в первом слое и гиперболический тангенс во втором слое:
  

; (12)

• гипотеза – НС с одним скрытым слоем с функцией активации (12);
  
• гипотеза – НС с двумя скрытыми слоями с функцией активации (12) в обоих слоях;
  
• гипотеза – НС с двумя скрытыми слоями с функцией активации (12) в первом слое и (11) во втором слое.
  

В табл. 1 приведены прогнозные значения показателя Ф для объекта № 2 (школа-лицей) в ансамбле НСМ (гипотез ).


Таблица 1


Результаты моделирования для объекта № 2

НСМ
Ф	0,0265	0,0235	0,0238	0,0272	0,0245	0,0243
	11%	2%	1%	13%	7%	3%

Для оценки ошибки прогноза выбрана точка горизонта прогноза (t = 21 месяц), где были известны данные. В таблице также приведена относительная ошибка аппроксимации  (в процентах). Максимальная ошибка по ансамблю составила 13%, средняя ошибка равна 6,5%.

Взаимная согласованность гипотез в ансамбле наглядно видна из динамических кривых на рис. 1 для объекта № 2. Здесь представлено фактическое значение показателя: Ф, прогнозное значение по НСМ: Ф расчетное по НС1 - НС6 и осредненное значение прогнозного показателя.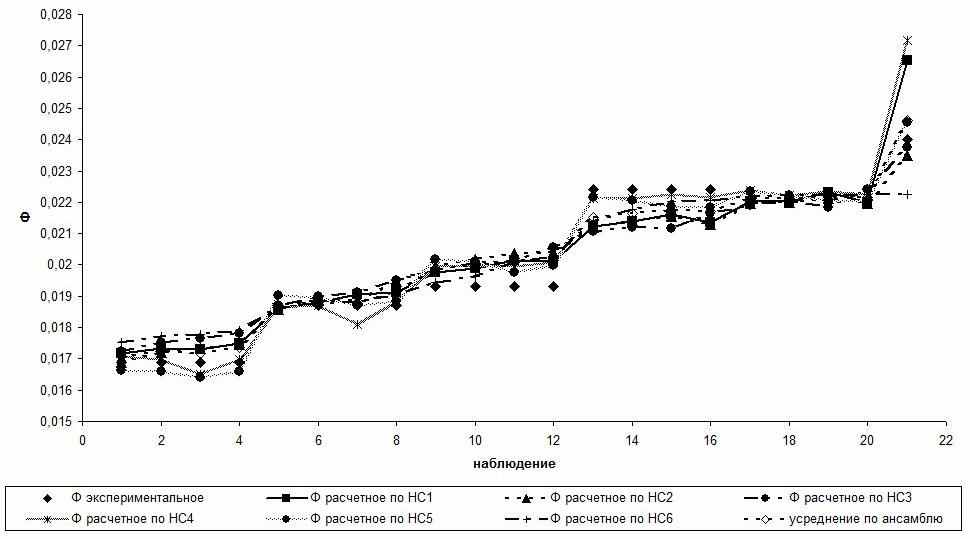







Рис. 1. Прогноз показателя Ф по второму объекту


Таким образом, предварительные вычислительные эксперименты на реальных данных [2] показали работоспособность предлагаемого подхода к регуляризации НСМ на основе байесовского подхода.


Список литературы

1. Горбатков С.А., Полупанов Д.В. Методы нейроматематики в налоговом контроле / Под ред. д.т.н., проф. С.А. Горбаткова. – Уфа: РИЦ БашГУ, 2008. – 136 с.
   
2. Гатауллин Р.Ф., Горбатков С.А., Бирюков А.Н., Глущенко О.И. Моделирование бюджетных процессов на муниципальном уровне на основе нейросетей. – Уфа: Изд-во Восточного университета, 2008. – 220 с.
   
3. Бэстенс Д.-Э., Ван-ден-Берг В.-М., Вуд Д. Нейронные сети и финансовые рынки: принятие решений в торговых операциях. – М.: Научное изд-во ТВП, 1997. – 235 с.
   
4. Тихонов А.Н., Кальнер В.Д., Гласко В.Б. Математическое моделирование технологических процессов и метод обратных задач в машиностроении. – М.: Машиностроение, 1990. – 264 с.
   
5. Тихонов А.Н., Леонов А.С., Ягола А.Г. Нелинейные некорректные задачи. – М.: Наука, 1995. – 312 с.
   
6. Федотов А.М. Некорректные задачи со случайными ошибками в данных - Новосибирск: Наука. Сибирское отделение, 1990. – 280 с.
   
7. Шумский С.А. Байесова регуляризация обучения // Научная сессия МИФИ-2002. IV Научно-техническая конференция «Нейроинформатика – 2002»: Лекции по нейроинформатике. Часть 2. – М.: МИФИ, 2002. – С. 30-93.
   
8. Хайкин С. Нейронные сети: полный курс. – М.: Изд. дом «Вильямс». – 1104 с.
   
9. Горбатков С.А., Фархиева С.А., Бесхлебнова Г.А. Об одном алгоритме предобработки сильнозашумленных входных данных в аспекте обеспечения состоятельности задачи регуляризации для нейросетевых моделей // Научная сессия МИФИ-2009. XI Научно-техническая конференция «Нейроинформатика-2008»: Сборник научных трудов. В 2-х частях Часть 1. – М.: МИФИ, 2009.– С. 18-26.
   
10. Горбатков С.А., Полупанов Д.В. Повышение качества гибридных нейросетевых моделей ранжирования объектов налогового контроля с помощью метода вложенных математических моделей // Научная сессия МИФИ-2008. X Научно-техническая конференция «Нейроинформатика-2008»: Сборник научных трудов. В 2-х частях Часть 1. – М.: МИФИ, 2008.– С. 41-51.
    

11. Gorbatkov S.A., Polupanov D.V. The regularization of neural networks for economioc objects with a strong data distraction // Материалы XV Международной конференции по нейрокибернетики. Том 2. Симпозиум «Интерфейс “Мозг-Компьютер”», 3-й Симпозиум по нейроинформатике и нейрокомпьютерам. – Ростов-на-Дону: Изд-во ЮФУ, 2009. – С. 263-266.

12. Горбатков С.А., Полупанов Д.В. Концепция разработки алгоритмов обеспечения состоятельности задачи регуляризации нейросетевых моделей с сильным зашумлением данных // Нейроинформатика, ее приложение и анализ данных: материалы XVII Всеросс. Семинара. – Красноярск: ИПК СФУ, 2009. – С. 42-44.

13. Прангишвилли И.В. Системный подход и общесистемные закономерности. – М.: СИГНЕТ, 2000. – 528 с.