Isbn 978-5-7262-1226 нейроинформатика 2010
| Вид материала | Документы |
- Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 136.25kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 9.21kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 113.94kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 89.17kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 124.83kb.
- Isbn 978-5-7262-1226 нейроинформатика 2010, 86.68kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
- Isbn 978-5-7262-1375 нейроинформатика 2011, 127.94kb.
- Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.
ISBN 978-5-7262-1226-5. НЕЙРОИНФОРМАТИКА – 2010. Часть 2
М.В. КРЫЖАНОВСКИЙ, М.Ю. МАЛЬСАГОВ
Научно исследовательский институт системных исследований РАН, Москва
iont.niisi@gmail.com
УСКОРЕНИЕ МОДИФИЦИРОВАННОЙ ПРОЦЕДУРЫ
КЛИППИРОВАНИЯ1
Исследована возможность применения обобщенной процедуры клиппирования в задаче оптимизации квадратичного функционала
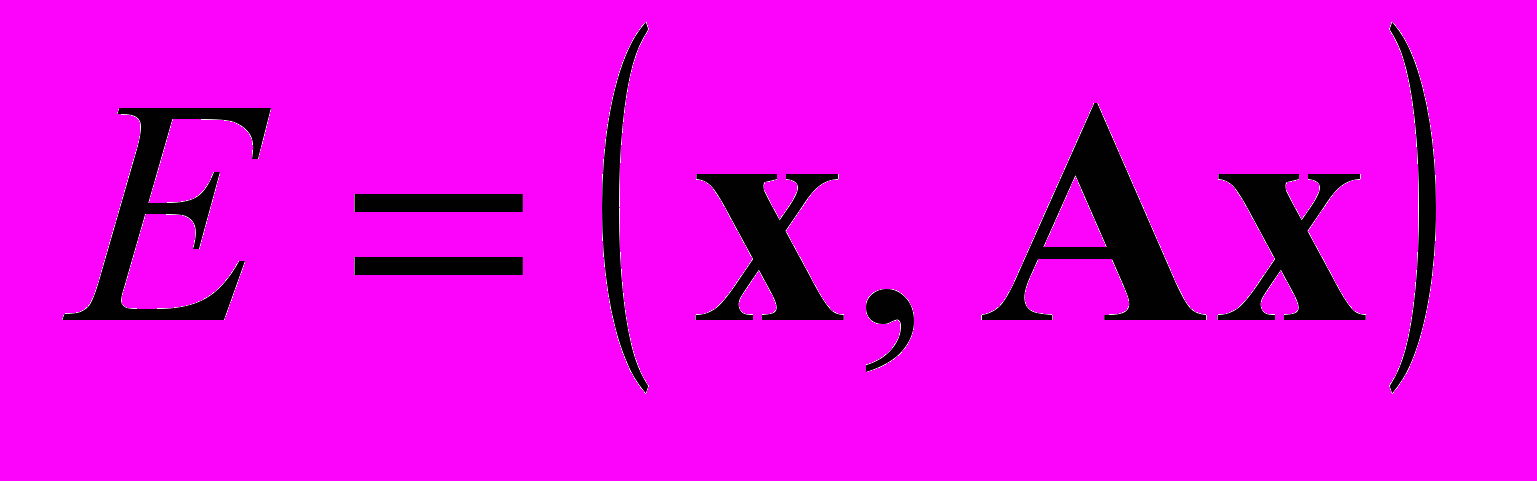 при поиске глобального минимума. Предложены модификации схемы поиска минимума и схемы расчета градиента, позволяющие ускорить поиск глобального минимума в 40 – 50 раз.
при поиске глобального минимума. Предложены модификации схемы поиска минимума и схемы расчета градиента, позволяющие ускорить поиск глобального минимума в 40 – 50 раз.Введение
Модифицированная процедура клиппирования [1] заключается в замене элементов матрицы межсвязей
 целыми числами по формуле (1):
целыми числами по формуле (1): , (1)
, (1)где
 – элемент клиппированной матрицы,
– элемент клиппированной матрицы, 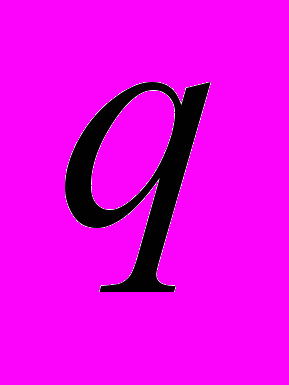 – число градаций, функция sgn дает знак числа, а функция round производит округление до ближайшего целого. Таким образом, все элементы исходной матрицы
– число градаций, функция sgn дает знак числа, а функция round производит округление до ближайшего целого. Таким образом, все элементы исходной матрицы  заменяются целыми числами в диапазоне
заменяются целыми числами в диапазоне 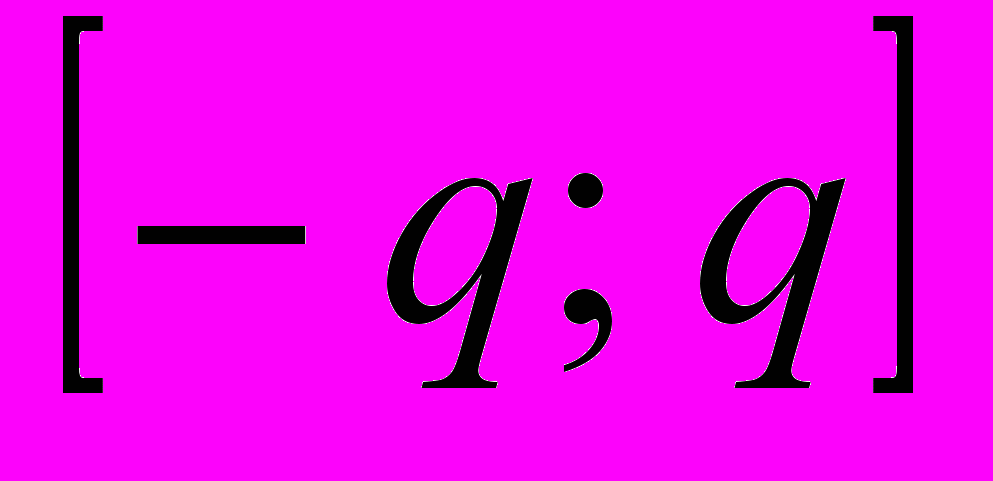 .
.Алгоритм поиска глобального минимума квадратичного функционала с использованием обобщенной процедуры клиппирования состоит из трех этапов: первый и второй этапы используют сеть Хопфилда с клиппированной матрицей межсвязей,
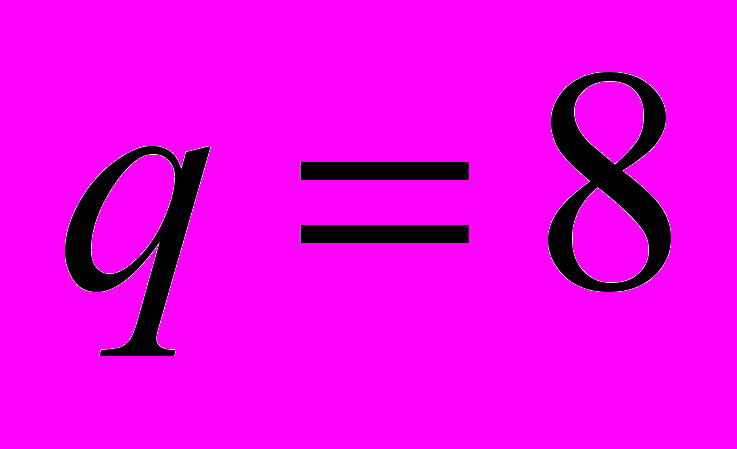 и
и 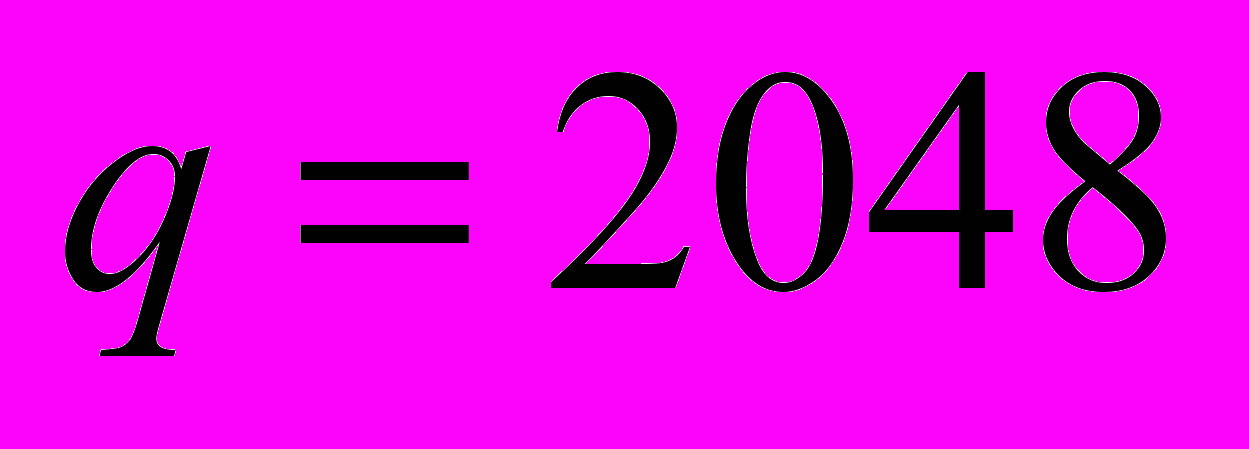 соответственно, на третьем производится коррекция состояний сети с исходной матрицей межсвязей.
соответственно, на третьем производится коррекция состояний сети с исходной матрицей межсвязей. В работе показано, что:
- С увеличением числа градаций вероятность совпадения градиентов увеличивается, и для данного
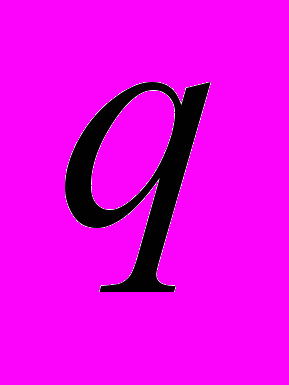 эта вероятность не зависит от размерности сети.
эта вероятность не зависит от размерности сети.
- Предлагаются модификации алгоритма поиска и схемы расчета градиента, которые позволяют дополнительно увеличить его быстродействие.
Клиппирование при поиске глобального минимума
Проанализируем корреляцию градиентов
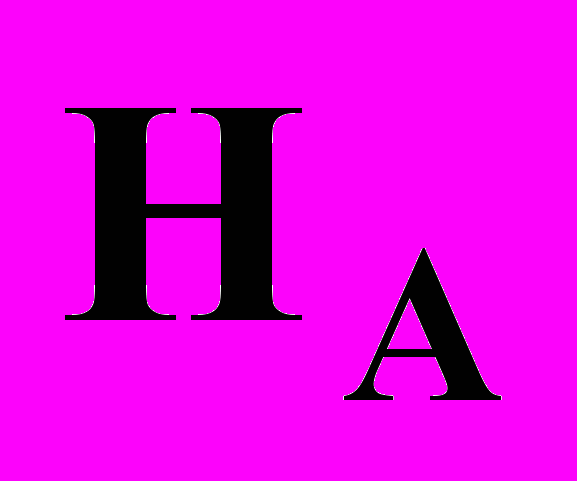 и
и 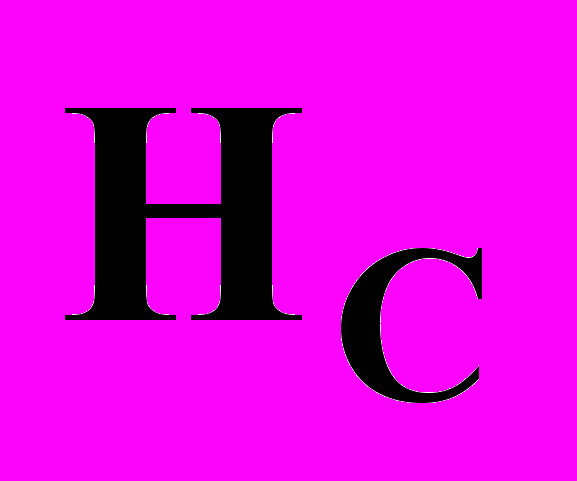 , т.е. локальных полей исходного функционала
, т.е. локальных полей исходного функционала 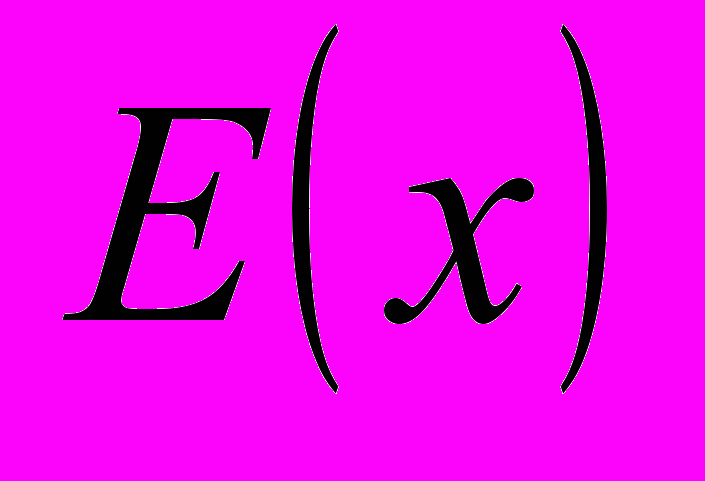 и клиппированного
и клиппированного 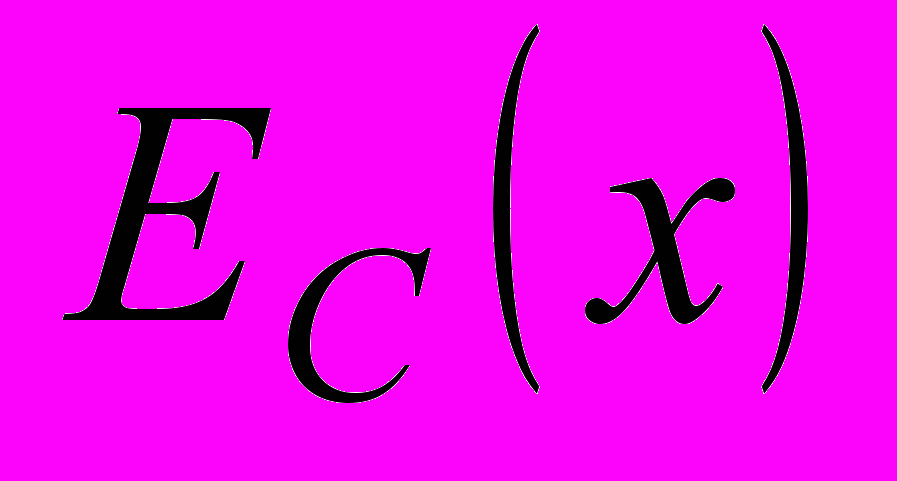 , которые имеют вид:
, которые имеют вид: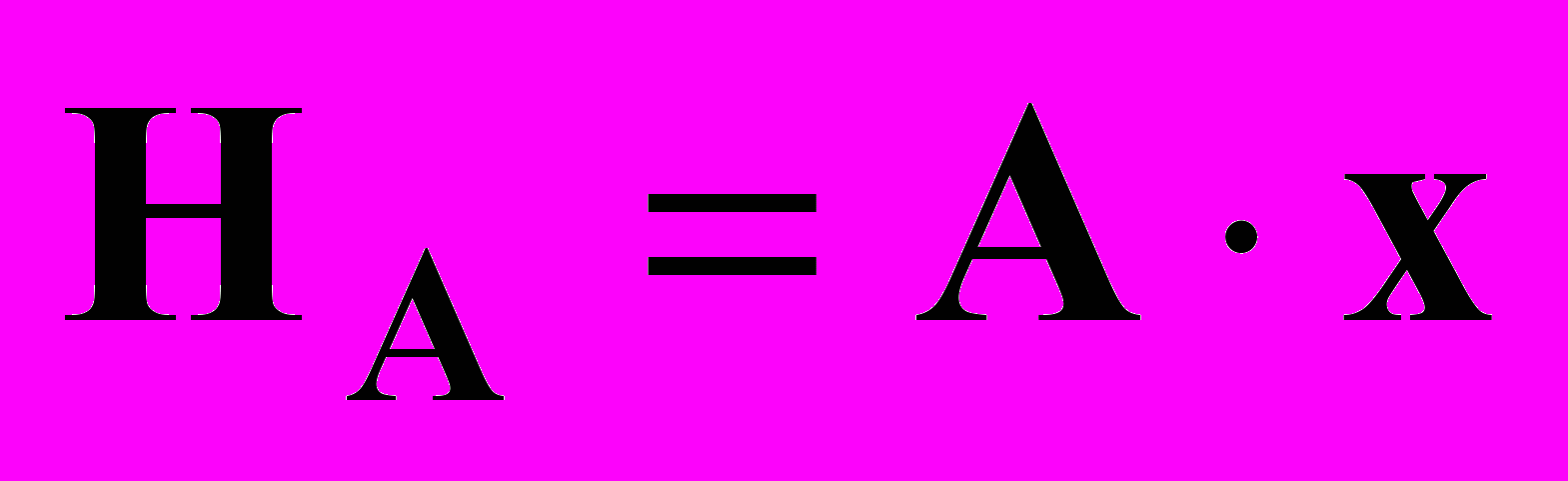 , (2)
, (2)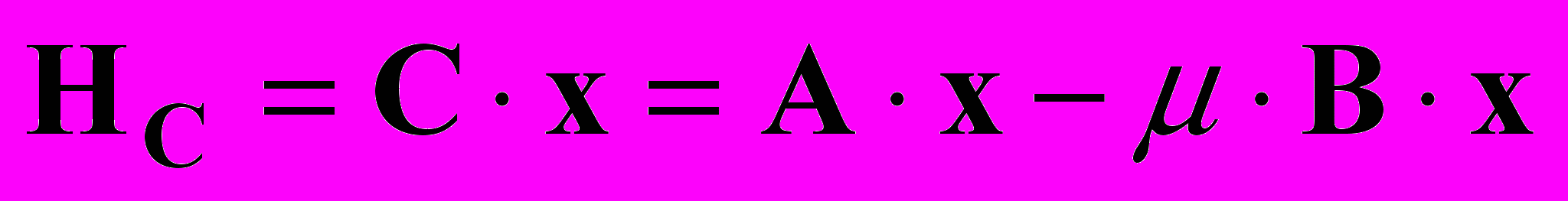 . (3)
. (3)Величина
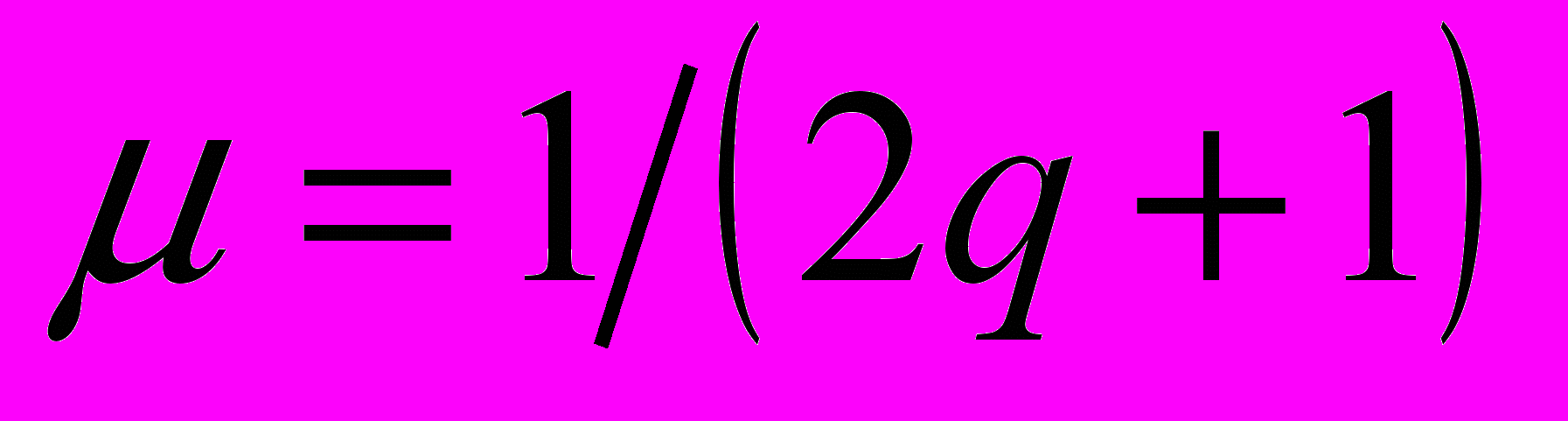 характеризует степень огрубления. Второе слагаемое в (3) характеризует остаток, получаемый от огрубления элементов
характеризует степень огрубления. Второе слагаемое в (3) характеризует остаток, получаемый от огрубления элементов  .
. 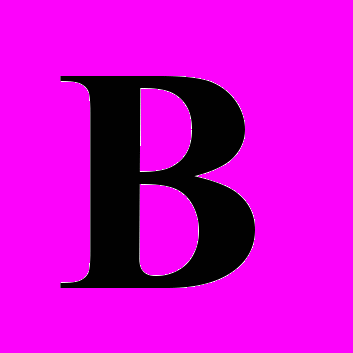 – матрица с равномерным случайным распределением элементов в диапазоне
– матрица с равномерным случайным распределением элементов в диапазоне 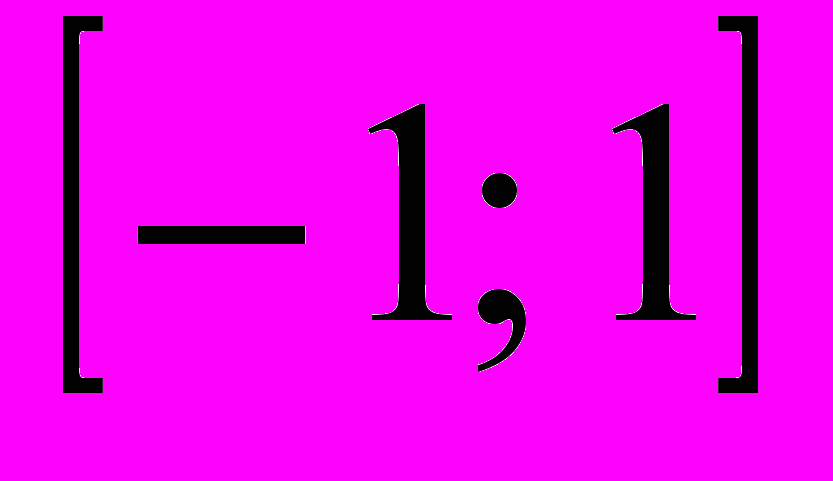 , а каждая компонента вектора
, а каждая компонента вектора 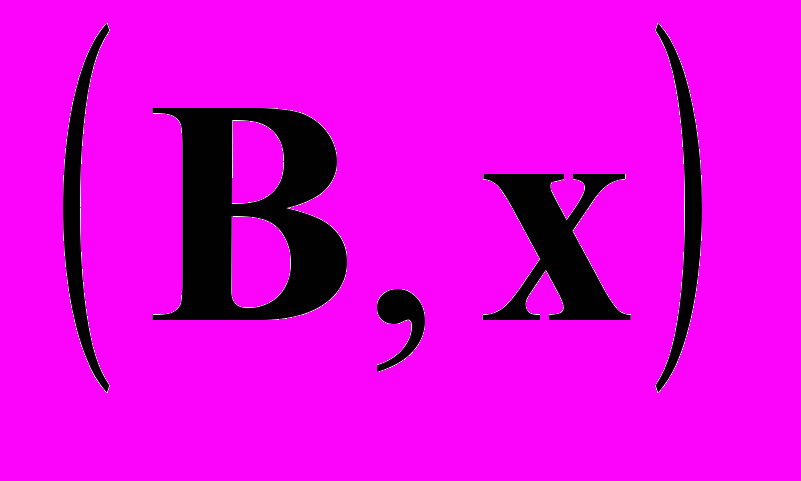 ведет себя как случайная величина, имеющая гауссово распределение
ведет себя как случайная величина, имеющая гауссово распределение 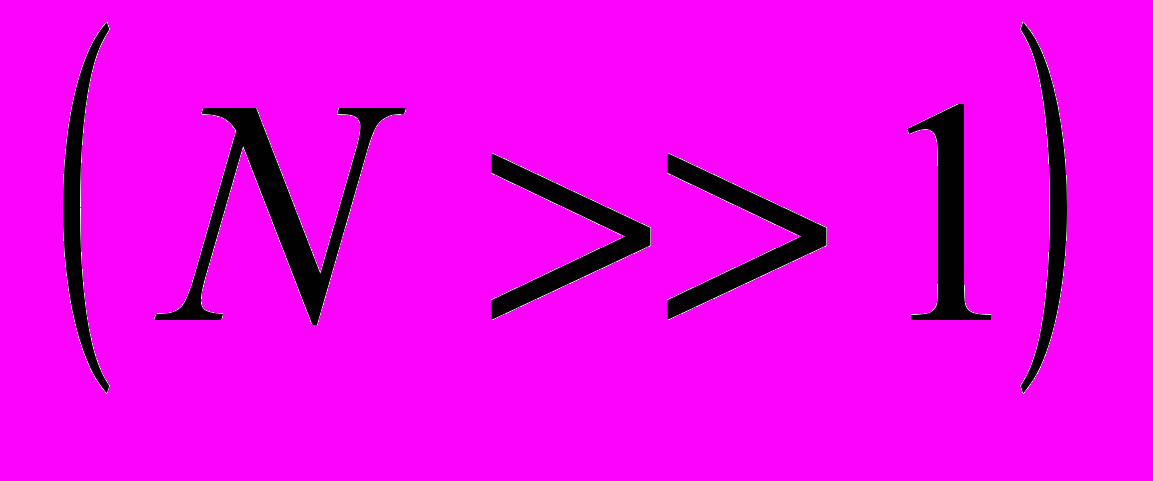 . Вычислим вероятность совпадения направления полей
. Вычислим вероятность совпадения направления полей 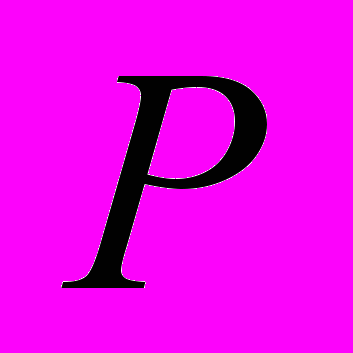 , т.е. совпадение по знаку каких-то компонент векторов
, т.е. совпадение по знаку каких-то компонент векторов 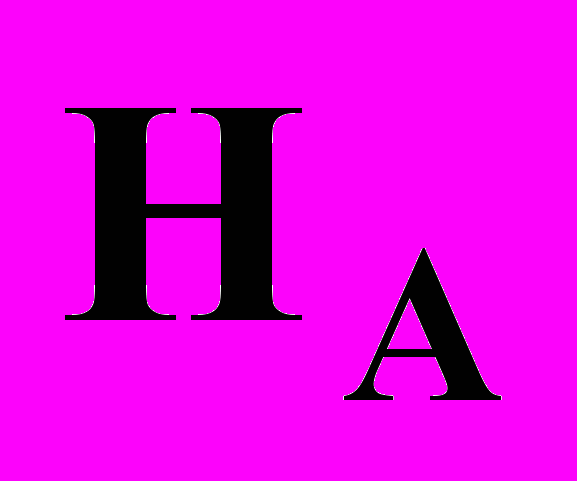 и
и 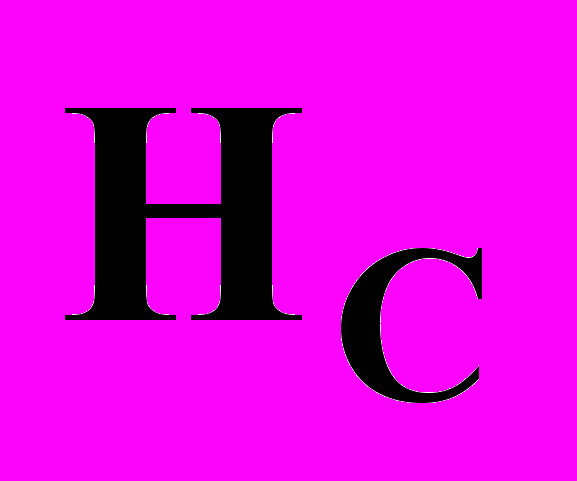 :
: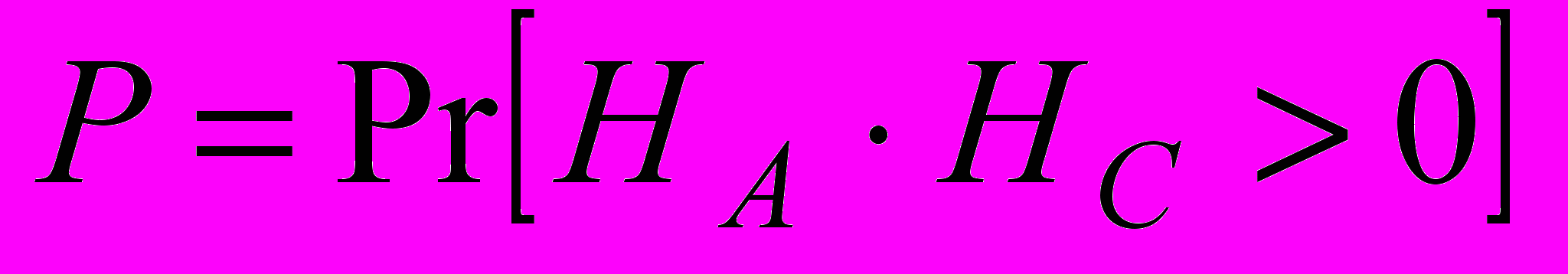 . (4)
. (4)Элементы исходной матрицы
 равномерно распределены с нулевым средним (
равномерно распределены с нулевым средним (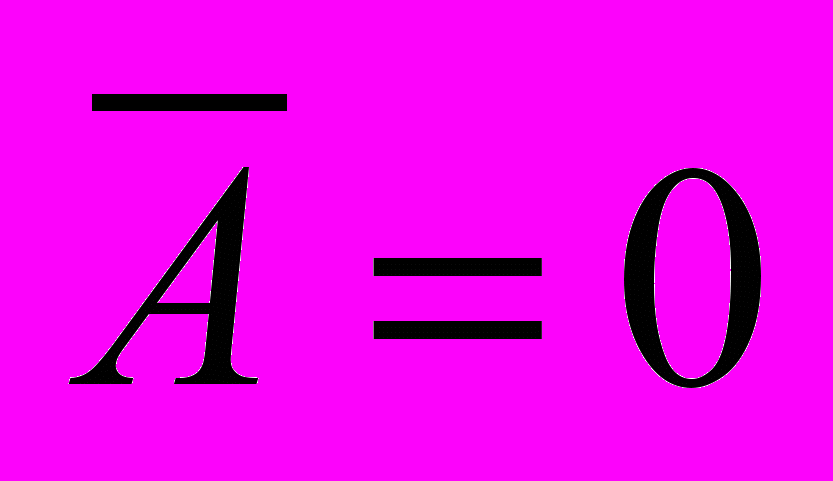 ) и дисперсией
) и дисперсией 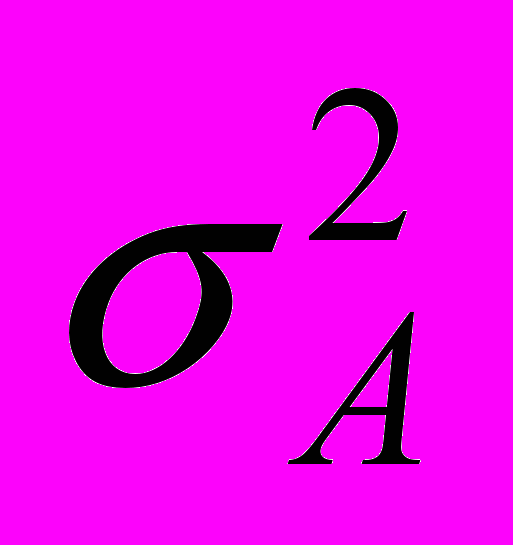 . С учетом выражений (2) и (3) можно показать, что математическое ожидание и дисперсия величин
. С учетом выражений (2) и (3) можно показать, что математическое ожидание и дисперсия величин 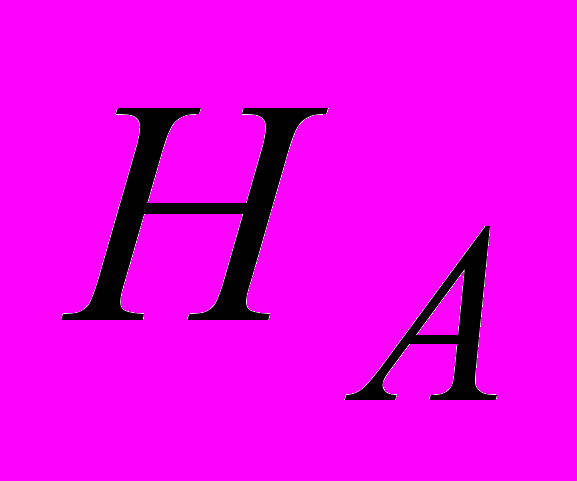 и
и 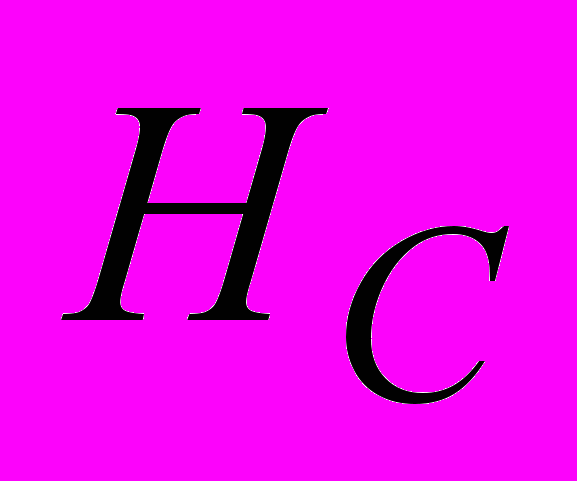 описываются выражениями:
описываются выражениями: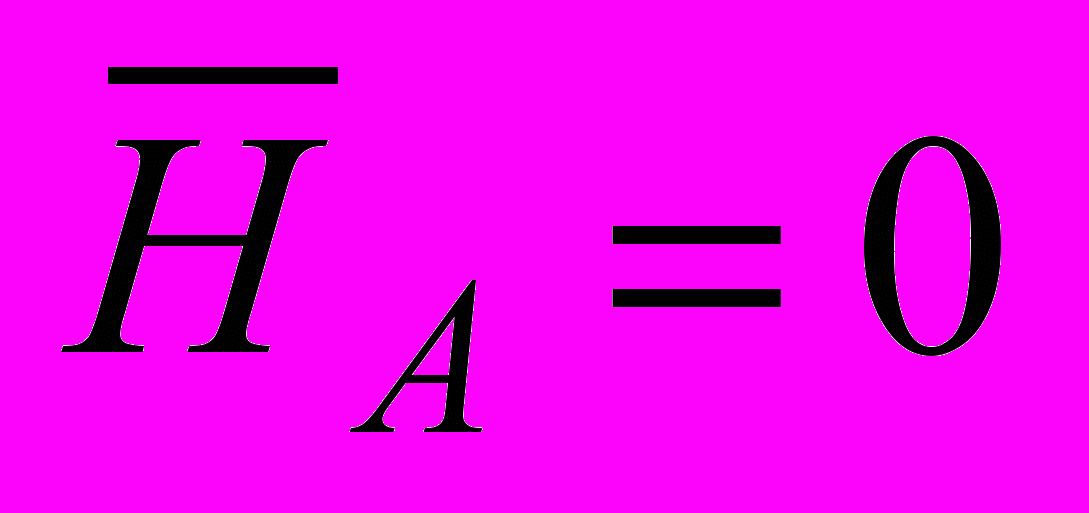 ,
, 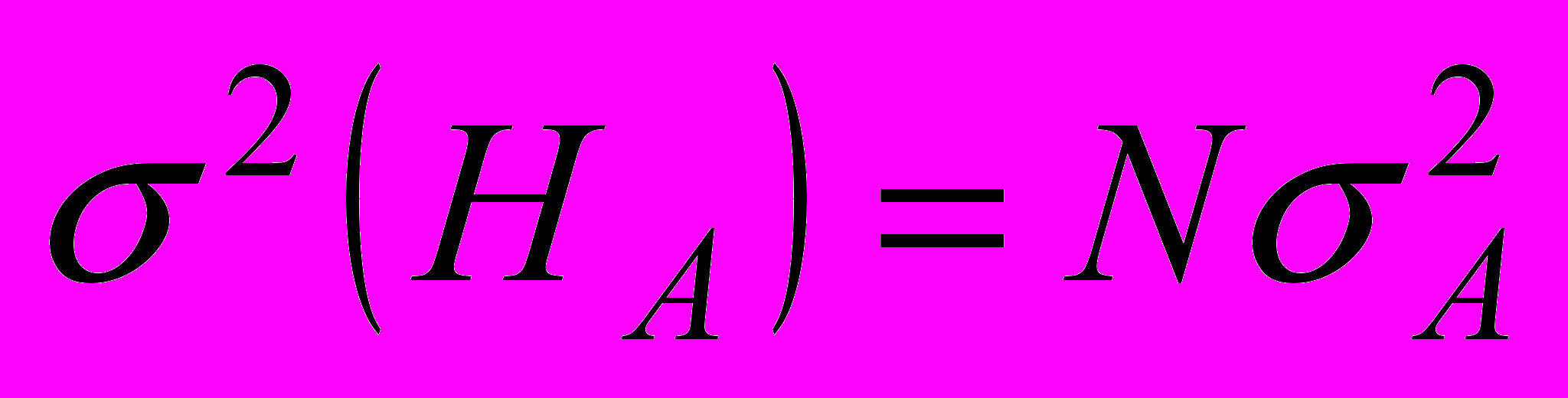 ; (5)
; (5)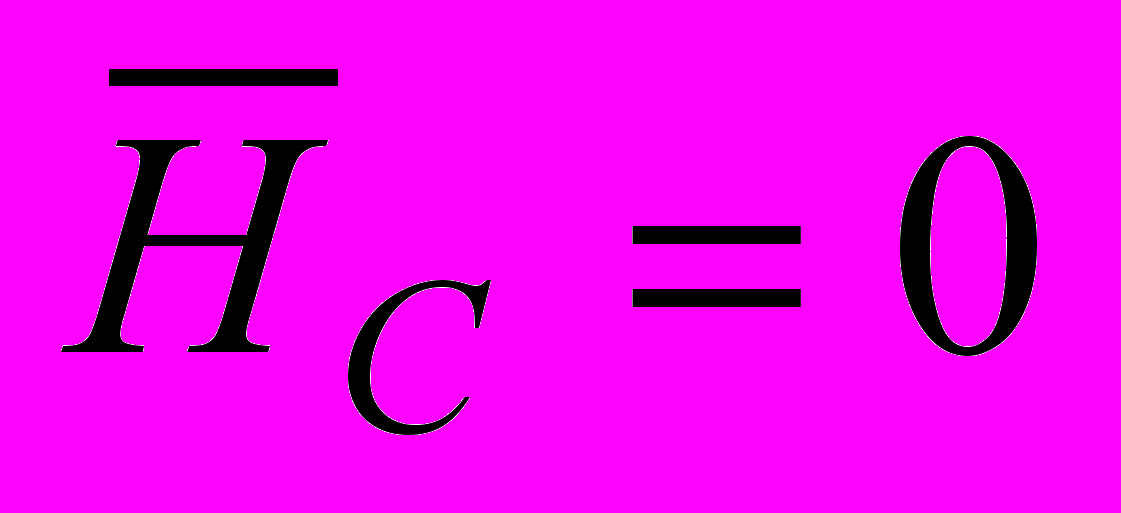 ,
, 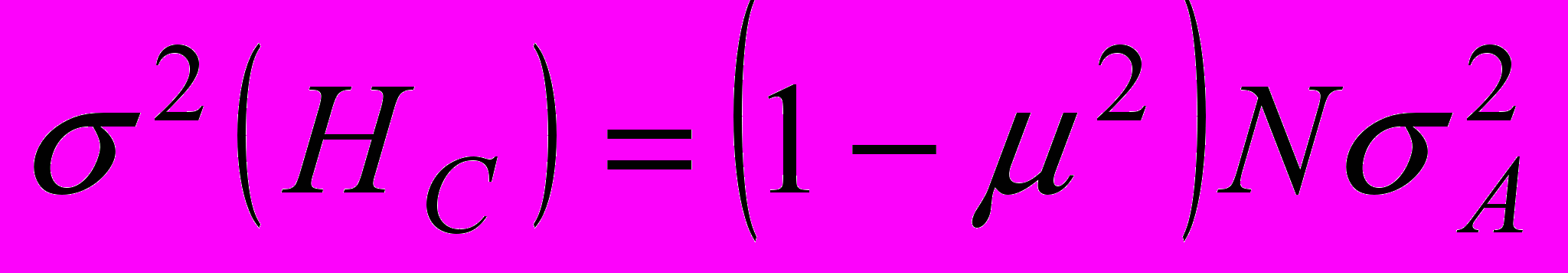 ; (6)
; (6)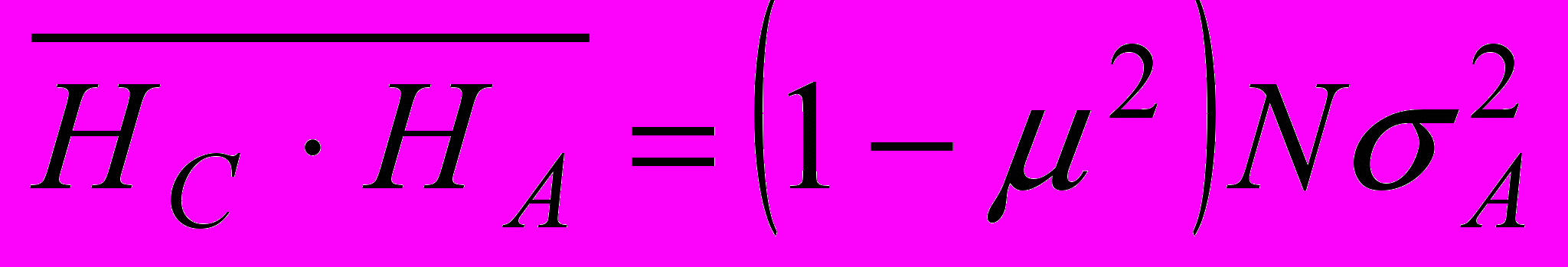 . (7)
. (7)С учетом выражений (5)-(7) коэффициент корреляции
 градиентов
градиентов 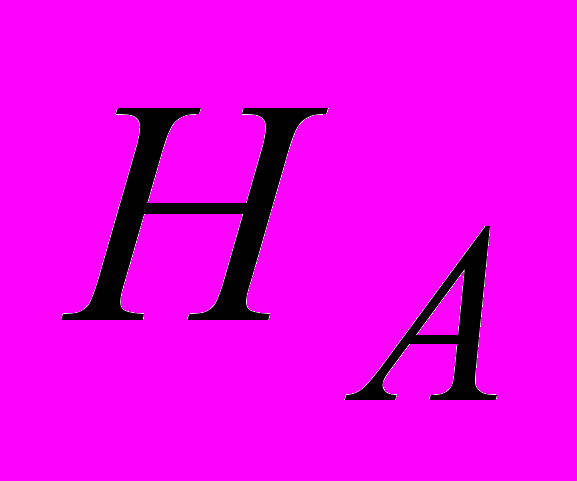 и
и 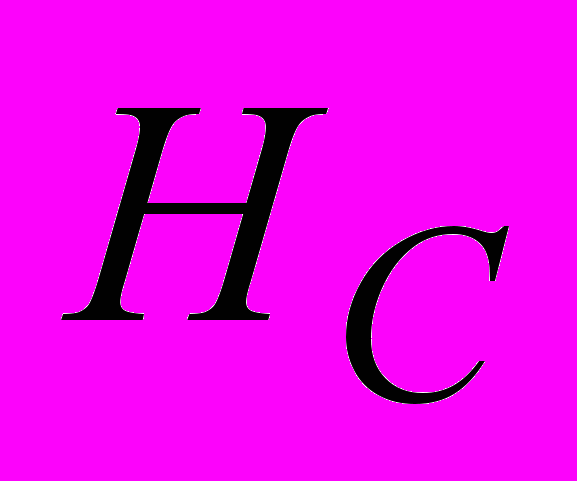 будет равен:
будет равен: . (8)
. (8)При
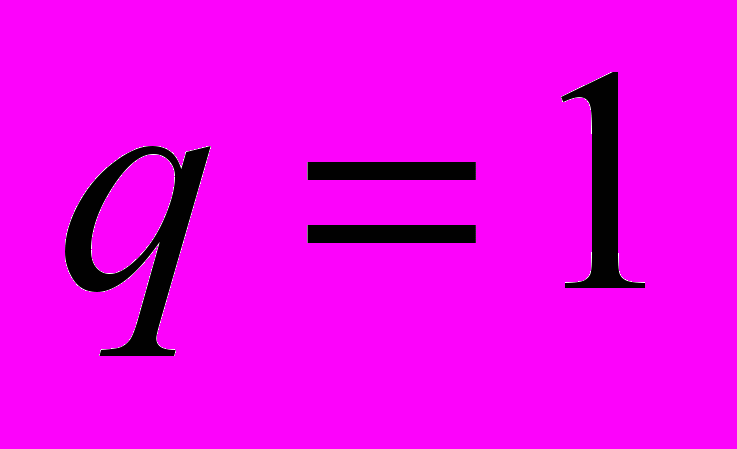 (или
(или 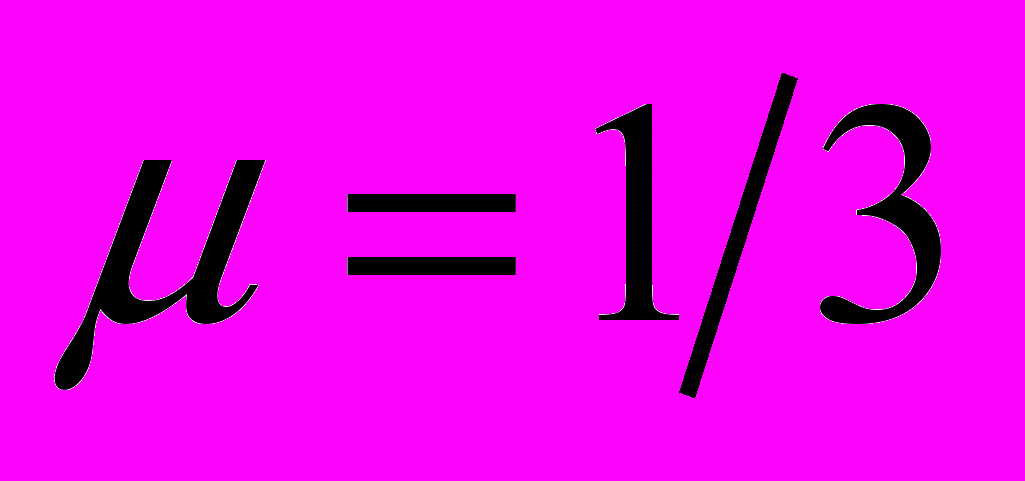 )
) 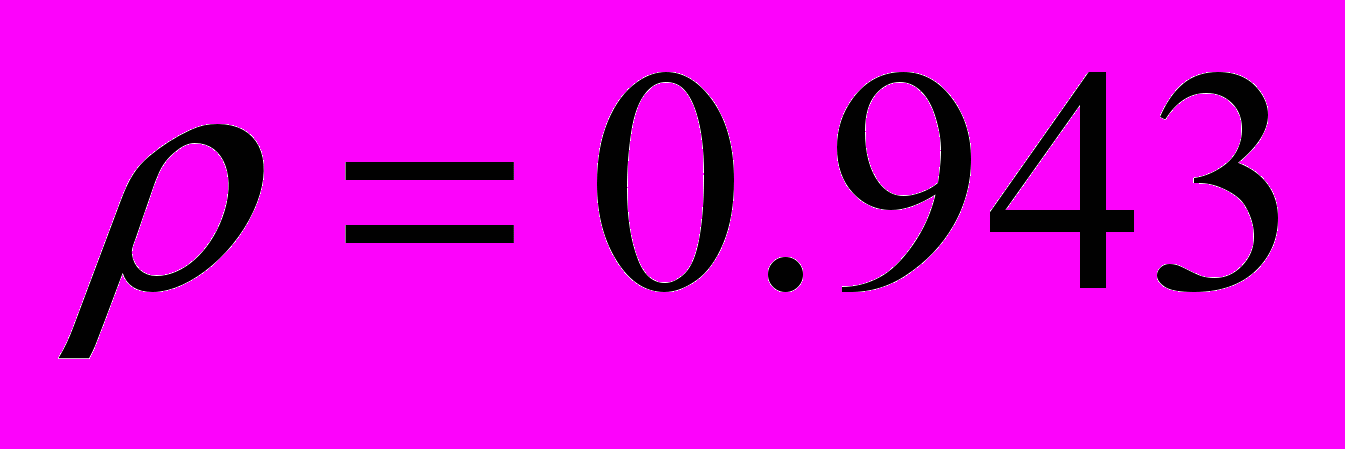 .
.В свою очередь вероятность совпадения направления полей
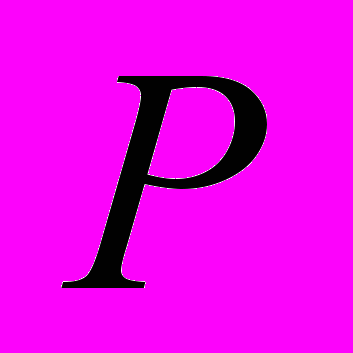 определяется как:
определяется как: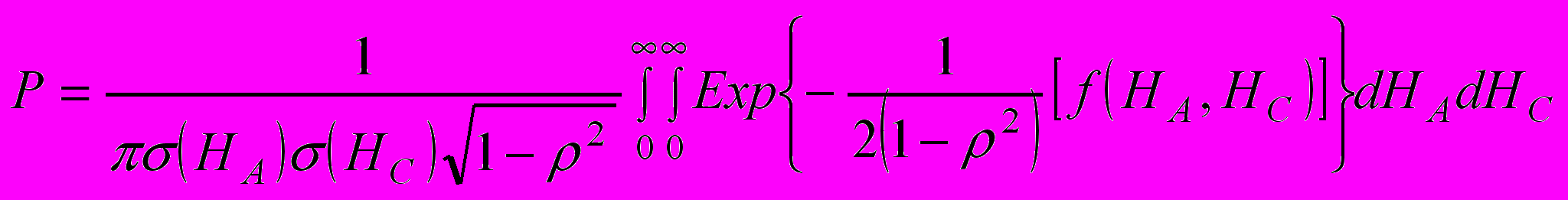 , (9)
, (9)где
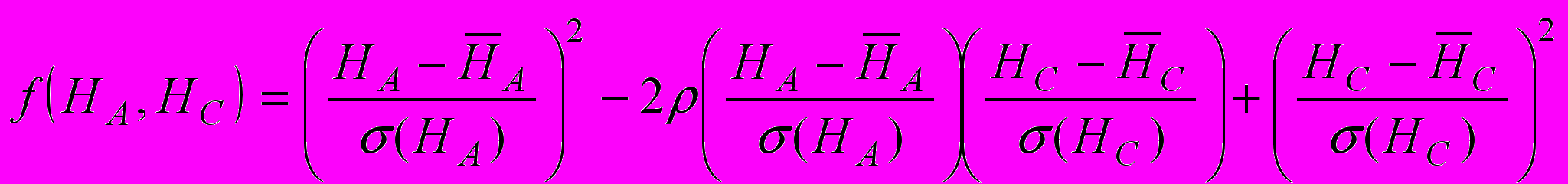 .
.Интеграл (9) сводится к формуле
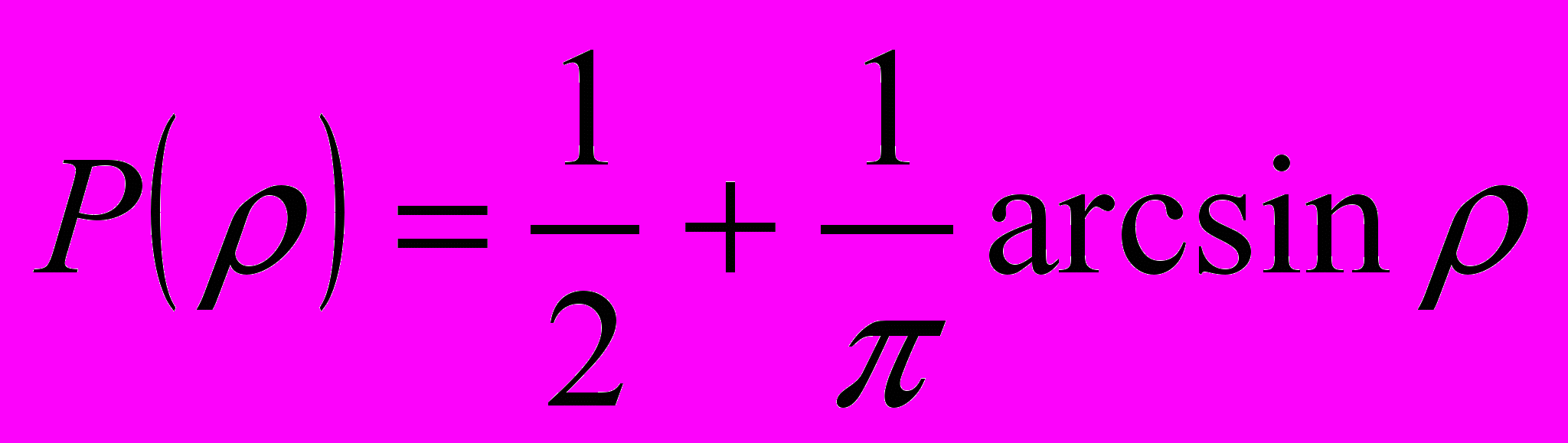 . (10)
. (10)Из приведенного на рис.1 графика, формул (9) и (10) следует, что локальные градиенты исходного и клиппированного функционалов с большой вероятностью совпадают
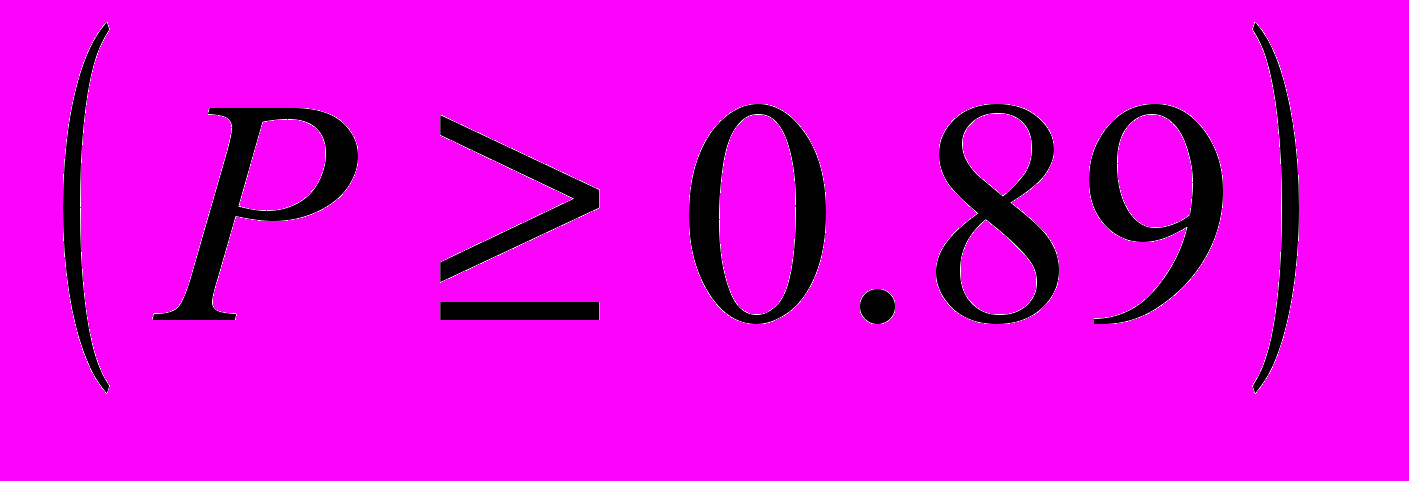 . С ростом числа градаций
. С ростом числа градаций 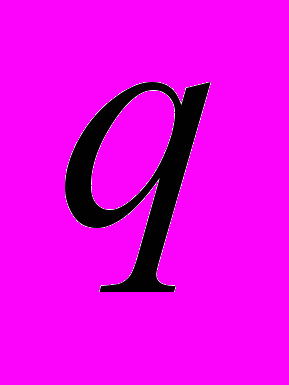 (уменьшение
(уменьшение  ) эта вероятность возрастает и стремится к 1. Поскольку процесс оптимизации заключается в последовательном перевороте всех
) эта вероятность возрастает и стремится к 1. Поскольку процесс оптимизации заключается в последовательном перевороте всех  спинов модели Хопфилда, то становится очевидным, что с ростом размерности задачи
спинов модели Хопфилда, то становится очевидным, что с ростом размерности задачи 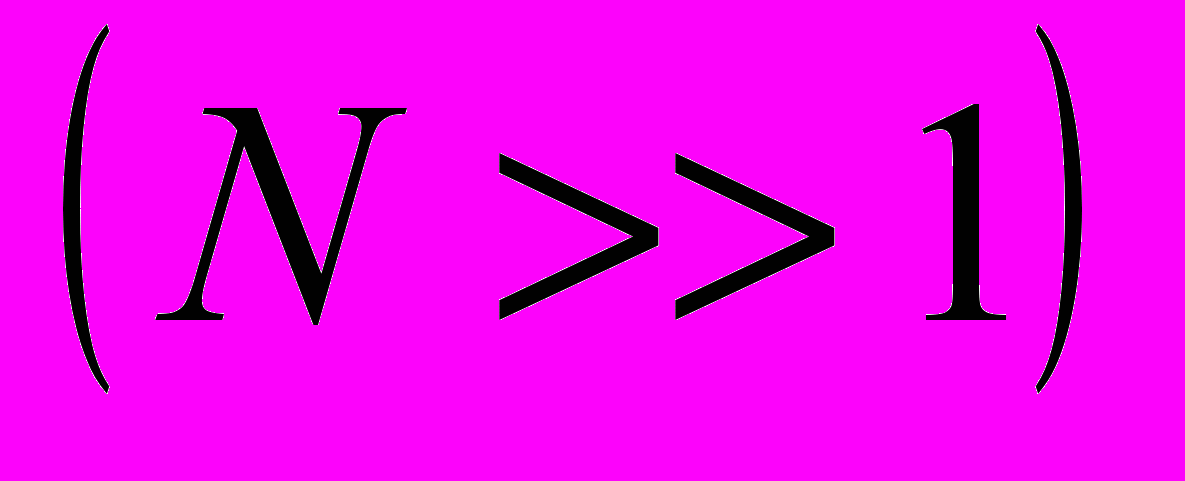 асимптотически стремится к нулю вероятность того, что в процессе оптимизации функционала энергия
асимптотически стремится к нулю вероятность того, что в процессе оптимизации функционала энергия 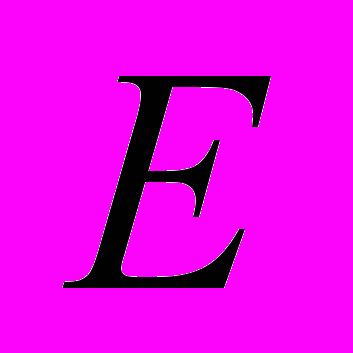 повысится.
повысится.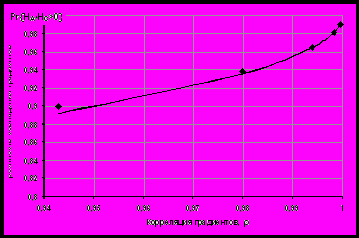
Рис. 1. Вероятность совпадения градиентов клиппированного и исходного функционалов в зависимости от коэффициента корреляции в случайной точке. (Сплошная линия – теоретическая зависимость (10), точки – экспериментальные данные)
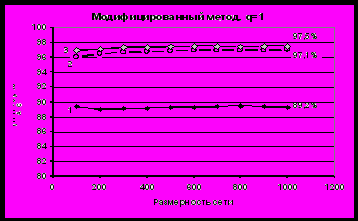
Рис. 2. Вероятность совпадения градиентов при использовании обобщенной процедуры клиппирования (кривая 1 – в случайной точке, кривая 2 – в точках минимума клиппированного функционала, кривая 3 – в точках минимума исходного функционала)
Полученные теоретические результаты точно согласуются с экспериментальными данными (рис. 1). Так измеренная экспериментально вероятность совпадения градиентов для модифицированного метода при
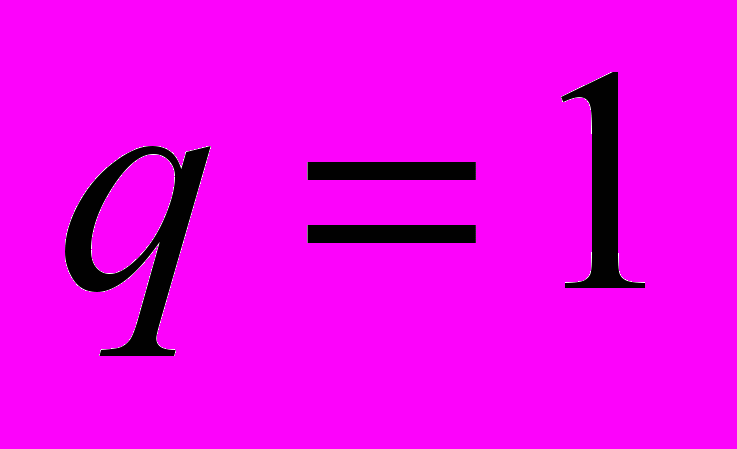 дает
дает 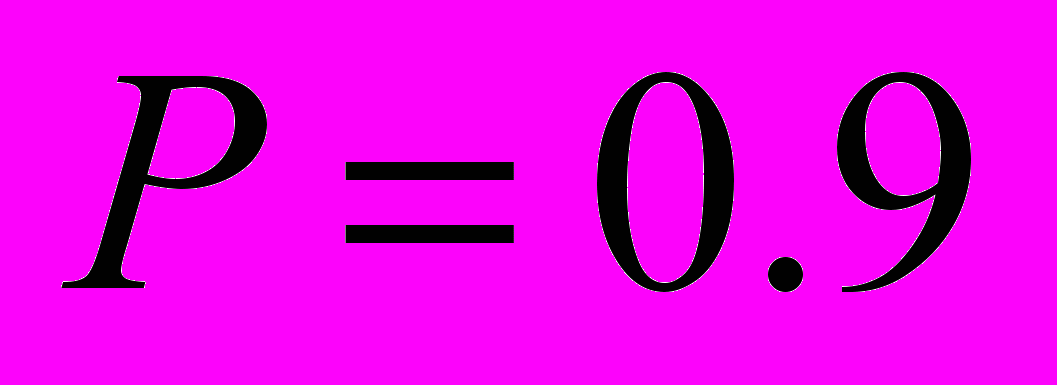 , в то же время, расчетное значение составляет
, в то же время, расчетное значение составляет 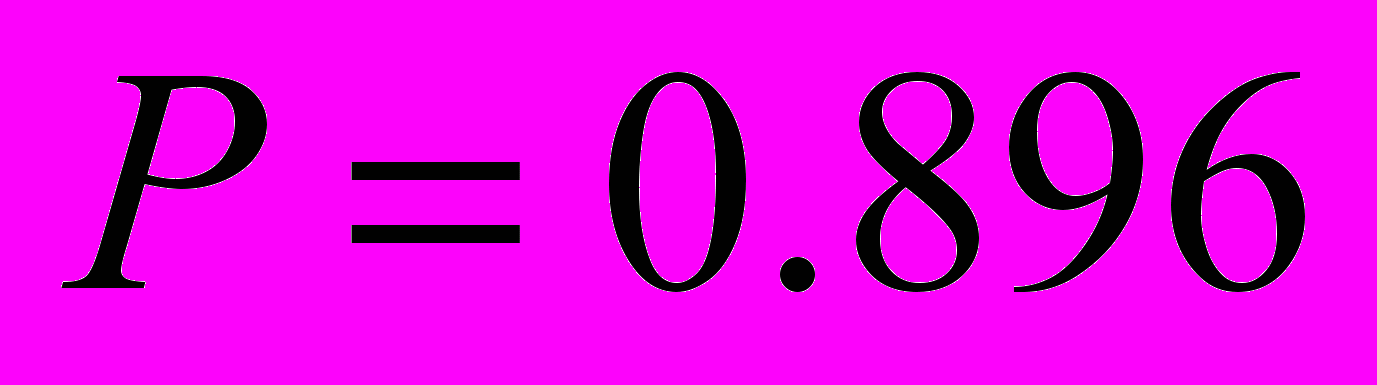 . В остальных точках совпадение полное.
. В остальных точках совпадение полное. На рис. 2 представлены экспериментальные данные вероятности совпадений градиентов
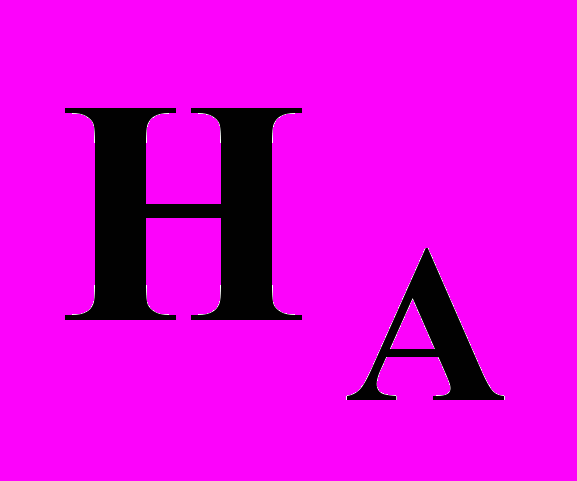 и
и 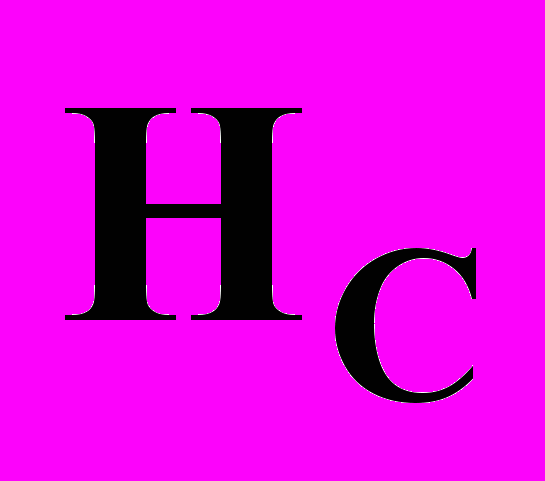 при использовании модифицированной процедуры клиппирования для
при использовании модифицированной процедуры клиппирования для 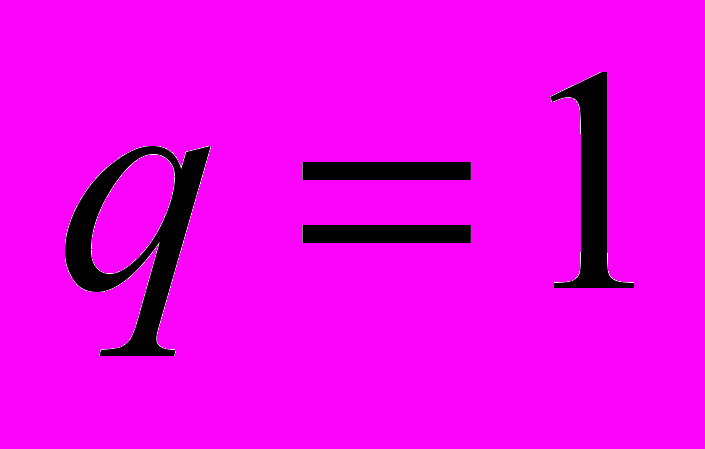 в различных точках (случайных, точках минимума клиппированного и исходного функционала). Видно, что эта вероятность не зависит от размерности сети.
в различных точках (случайных, точках минимума клиппированного и исходного функционала). Видно, что эта вероятность не зависит от размерности сети.Как следует из приведенных выше формул (8), (10) и экспериментальных результатов (рис. 1 и 2), вероятность совпадения градиентов возрастает с увеличением q и для фиксированного значения q эта вероятность не зависит от размерности сети.
Трехэтапный алгоритм клиппирования
Основной объем вычислений при расчетах нейронной сети Хопфилда приходится на вычисление градиентов, т.е. на операции умножения матрицы на вектор. Для матриц высокой размерности
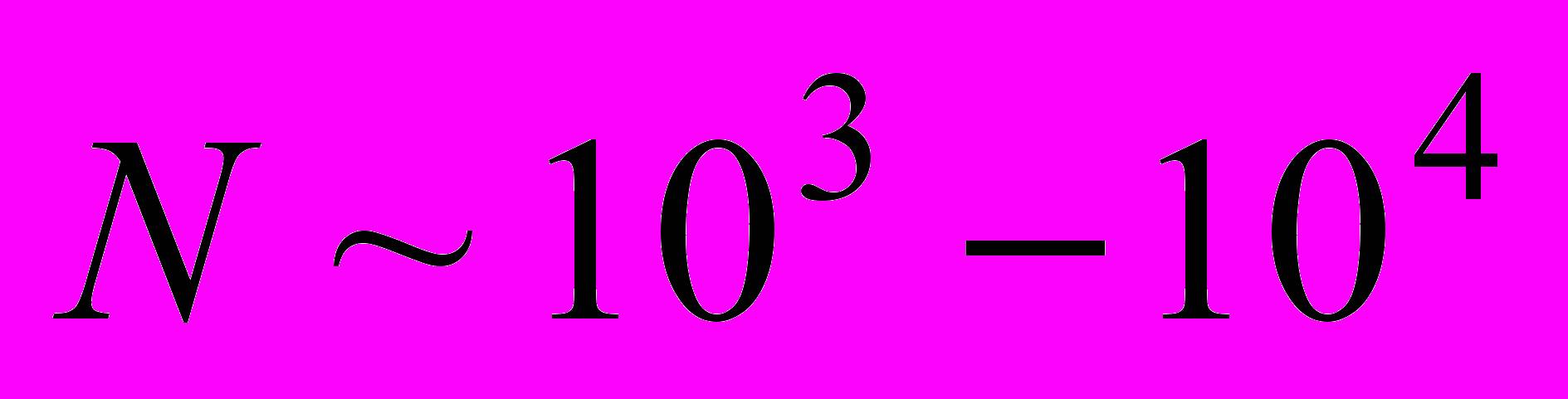 используется 10-байтное представление чисел для получения необходимой точности вычислений. Представление матрицы межсвязей нейронной сети с помощью чисел укороченной разрядности позволяет ускорить вычислительный процесс. Так, если сложение 2-х 10-байтных чисел требует 1-го такта процессорного времени, то для сложения 2-х десятимерных векторов, компоненты которых 1-байтные числа, потребуется времени меньше 1 такта. Кроме того, загрузка операндов из памяти в регистры процессора также требует время, сопоставимое со временем выполнения операции. Поэтому «эффективное» время выполнения 1-байтовой операции приблизительно в 15 раз меньше, чем 10-байтовой.
используется 10-байтное представление чисел для получения необходимой точности вычислений. Представление матрицы межсвязей нейронной сети с помощью чисел укороченной разрядности позволяет ускорить вычислительный процесс. Так, если сложение 2-х 10-байтных чисел требует 1-го такта процессорного времени, то для сложения 2-х десятимерных векторов, компоненты которых 1-байтные числа, потребуется времени меньше 1 такта. Кроме того, загрузка операндов из памяти в регистры процессора также требует время, сопоставимое со временем выполнения операции. Поэтому «эффективное» время выполнения 1-байтовой операции приблизительно в 15 раз меньше, чем 10-байтовой.Идея модификации заключается в применении целых чисел в одно- и двухбайтовом представлении для матричных элементов. Соответственно этому и был построен алгоритм спуска по «энергетической поверхности», который состоит из 3-х этапов, когда локальный минимум, полученный на текущем этапе, являлся начальным приближением для следующего этапа. На первом и втором этапах использовалась модификация клиппирования с числом градаций
 на 1-ом (однобайтные операции) и
на 1-ом (однобайтные операции) и 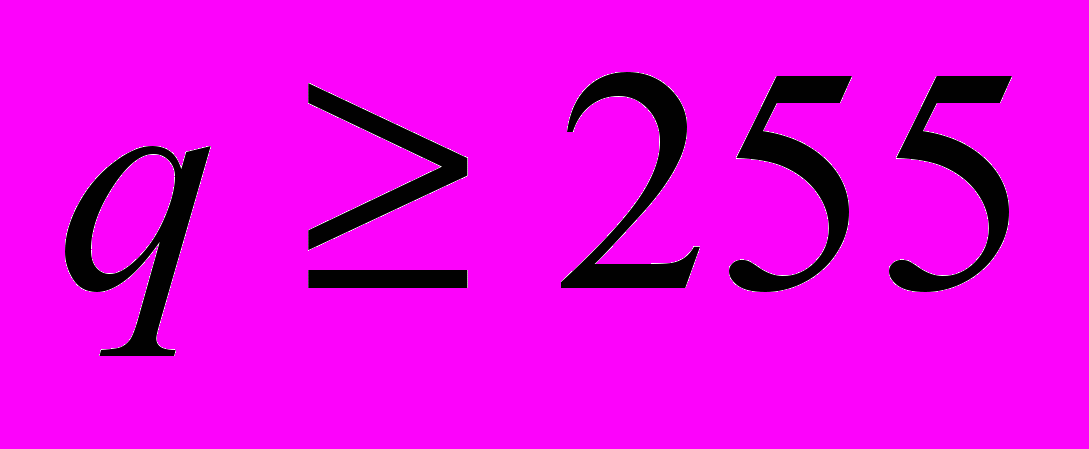 на 2-м (двухбайтные операции). Для коррекции состояний на третьем этапе использовалась стандартная сеть Хопфилда.
на 2-м (двухбайтные операции). Для коррекции состояний на третьем этапе использовалась стандартная сеть Хопфилда.Ускорение вычислительного процесса зависит от числа градаций
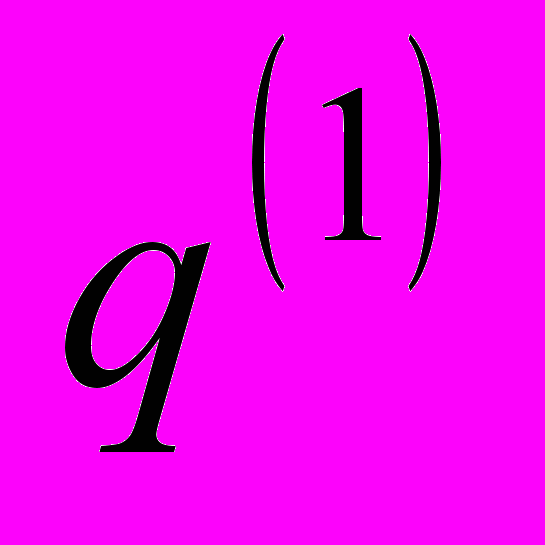 , выбранного на первом этапе. На втором этапе число
, выбранного на первом этапе. На втором этапе число 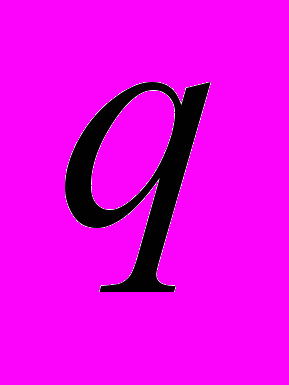 может быть выбрано максимально большим
может быть выбрано максимально большим  .
. Для определения оптимального значения
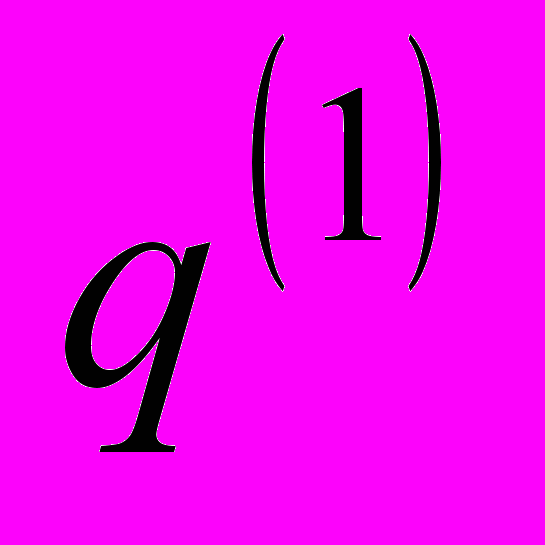 на 1-м этапе и соответственно величины ускорения алгоритма
на 1-м этапе и соответственно величины ускорения алгоритма  был проделан вычислительный эксперимент. На каждом этапе оптимизации функционала определялось число итераций при попадании в локальный минимум, которое пропорционально объему вычислений. При этом фиксировалось количество шагов при «спуске» с использованием исходной сети Хопфилда.
был проделан вычислительный эксперимент. На каждом этапе оптимизации функционала определялось число итераций при попадании в локальный минимум, которое пропорционально объему вычислений. При этом фиксировалось количество шагов при «спуске» с использованием исходной сети Хопфилда.Результаты вычислительного эксперимента приведены в табл. 1. Ускорение
 работы алгоритма определяется формулой (11).
работы алгоритма определяется формулой (11).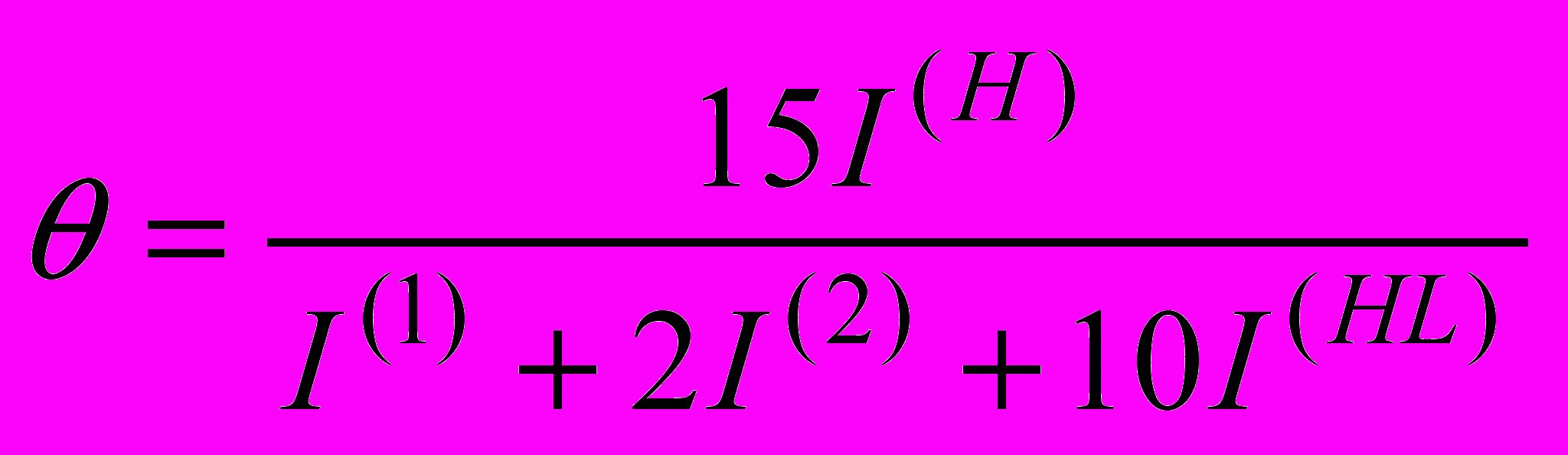 , (11)
, (11)где
 – число итераций, используя стандартный метод Хопфилда;
– число итераций, используя стандартный метод Хопфилда; 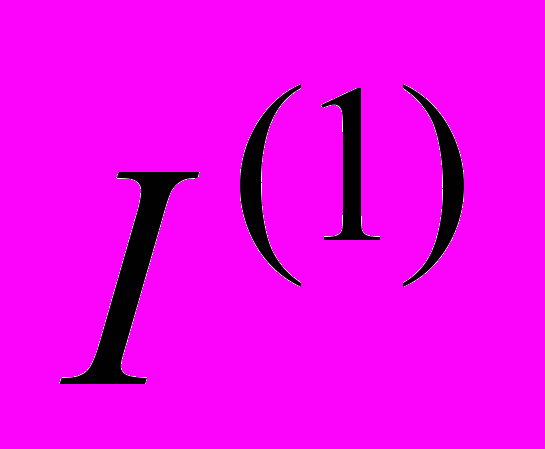 – число итераций на первом этапе (однобайтная арифметика);
– число итераций на первом этапе (однобайтная арифметика); 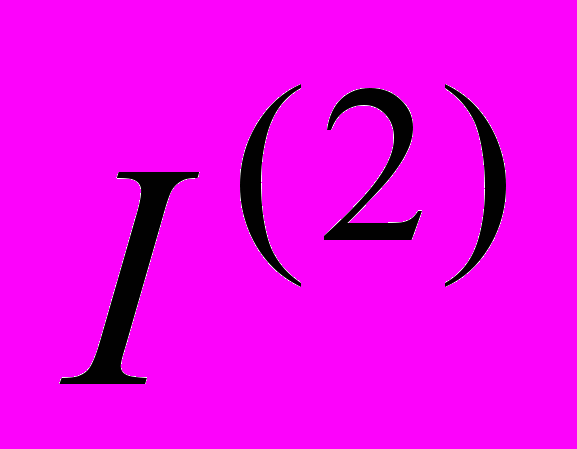 – число итераций на втором этапе (двухбайтные вычисления);
– число итераций на втором этапе (двухбайтные вычисления);  – число итераций на этапе коррекции состояний стандартным методом Хопфилда.
– число итераций на этапе коррекции состояний стандартным методом Хопфилда.Установлено, что в среднем
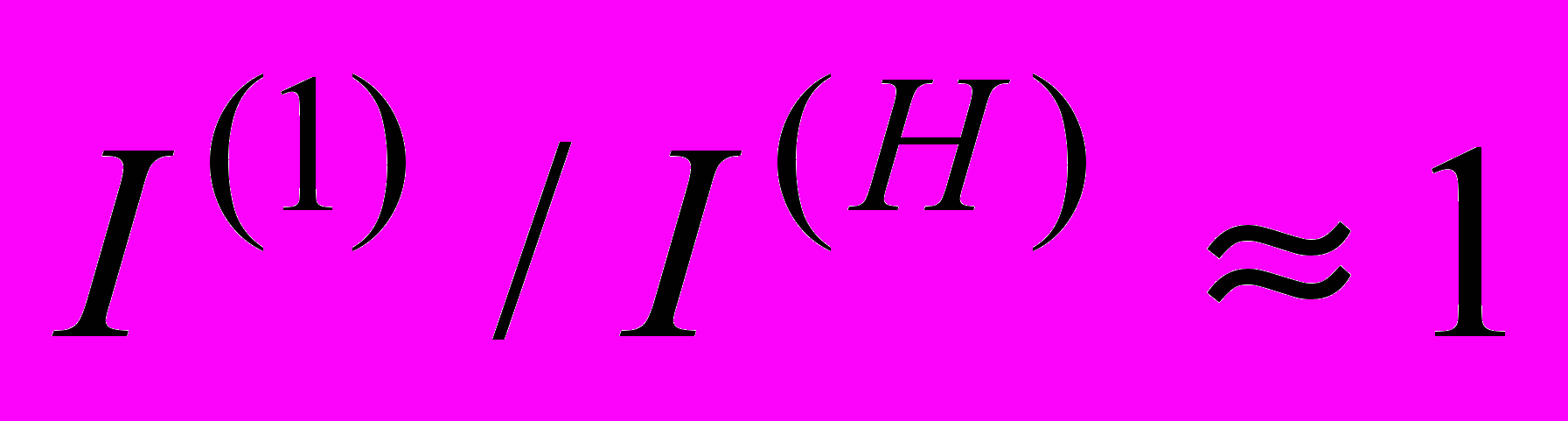 ;
; 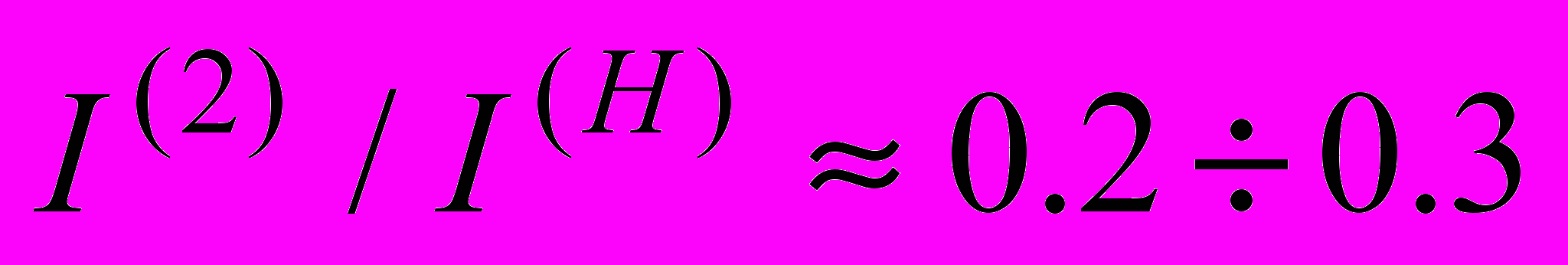 ;
; 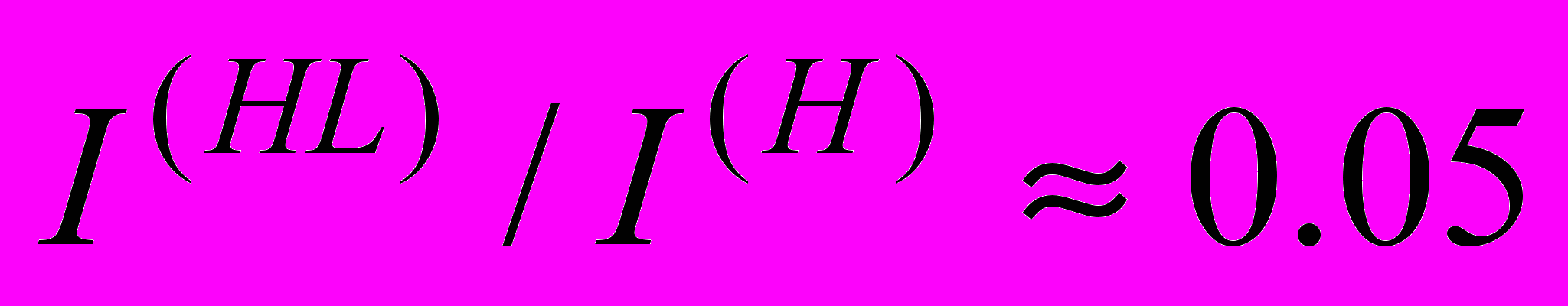 .
.Таблица 1
Ускорения алгоритма по сравнению со стандартным методом Хопфилда
в зависимости от значений параметра
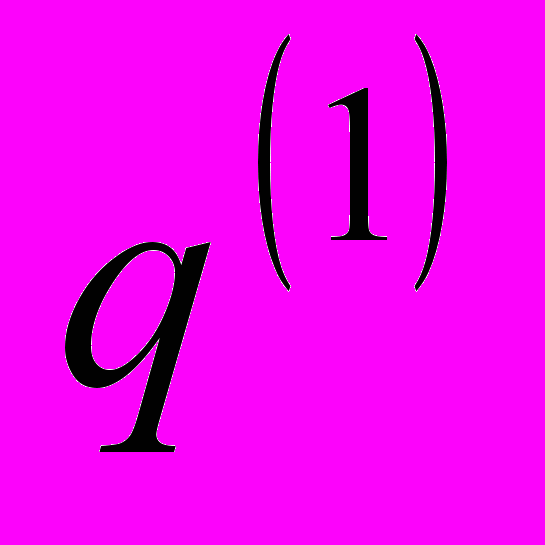
-
Размерность сети N = 256
Число градаций, q
Ускорение алгоритма, θ
2
3,3
4
4,3
8
7,9
12
10,3
15
11,2
32
6,4
64
3
Быстродействие алгоритма зависит от выбора параметра
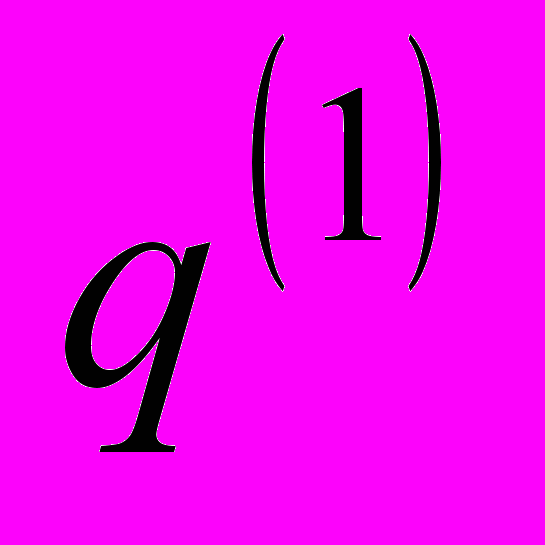 , применяемого на первом этапе. Так, в табл.1 приведены результаты экспериментов по увеличению скорости работы алгоритма
, применяемого на первом этапе. Так, в табл.1 приведены результаты экспериментов по увеличению скорости работы алгоритма 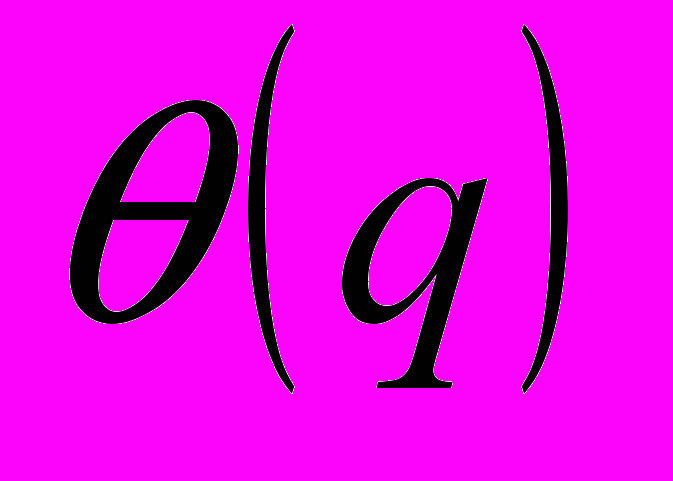 по сравнению с обычным методом Хопфилда. Результаты получены на матрице размерности
по сравнению с обычным методом Хопфилда. Результаты получены на матрице размерности 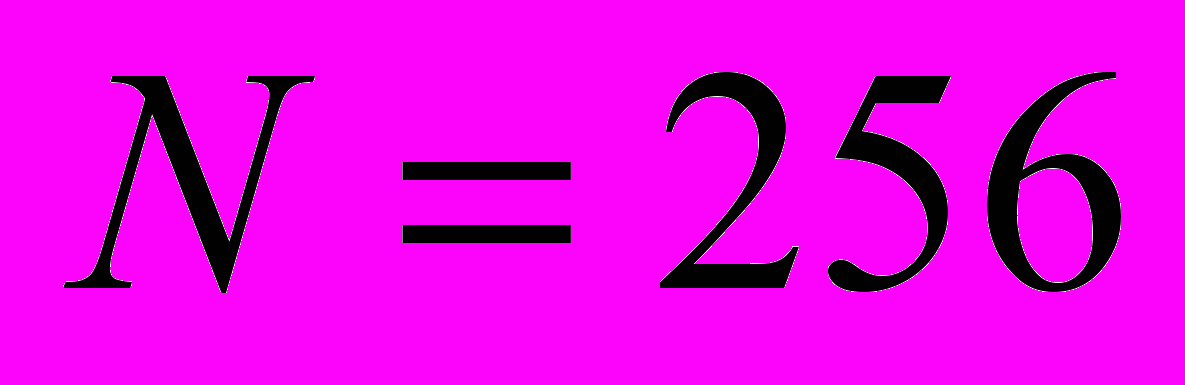 , и
, и 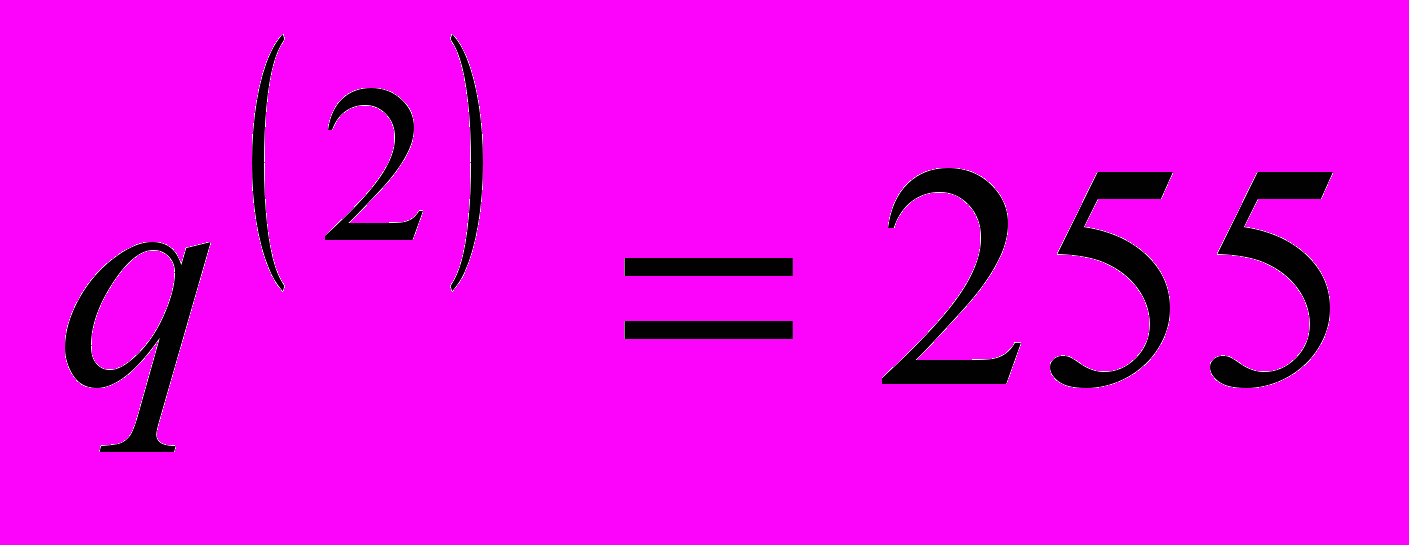 . Видно что, оптимум функции
. Видно что, оптимум функции 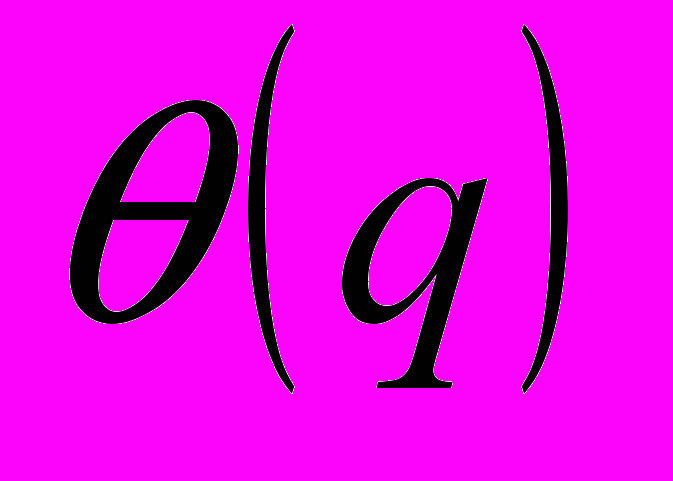 более 10 раз достигается при
более 10 раз достигается при 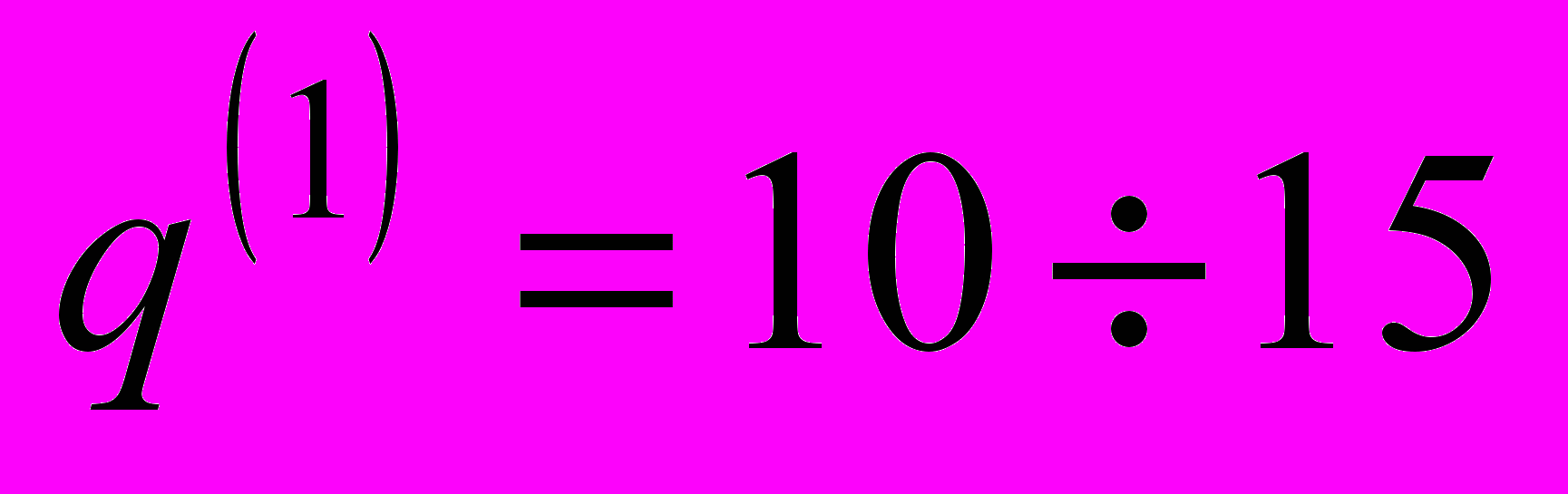 .
.При увеличении числа градаций на 2-м этапе число шагов на этапе коррекции состояний сокращается до 1. Поэтому на втором этапе должно быть выбрано максимальное значение
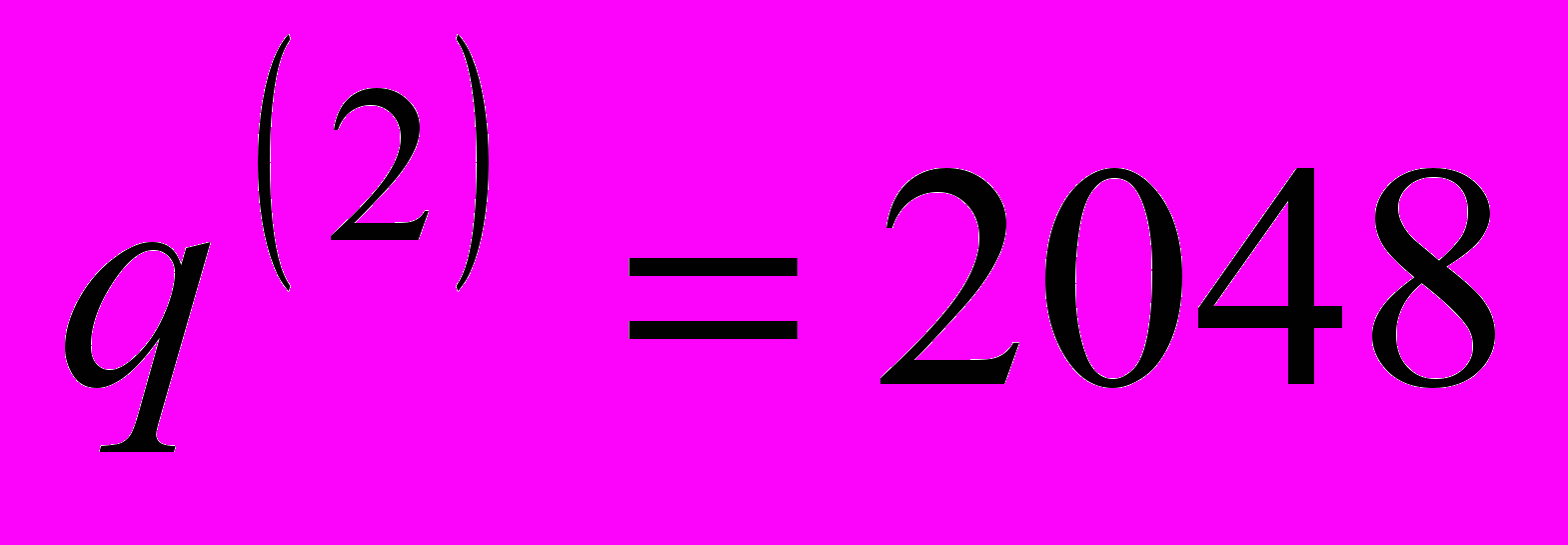 . В этом случае 3-й этап коррекции может быть не нужен. В этом случае формула (11) приобретает вид
. В этом случае 3-й этап коррекции может быть не нужен. В этом случае формула (11) приобретает вид 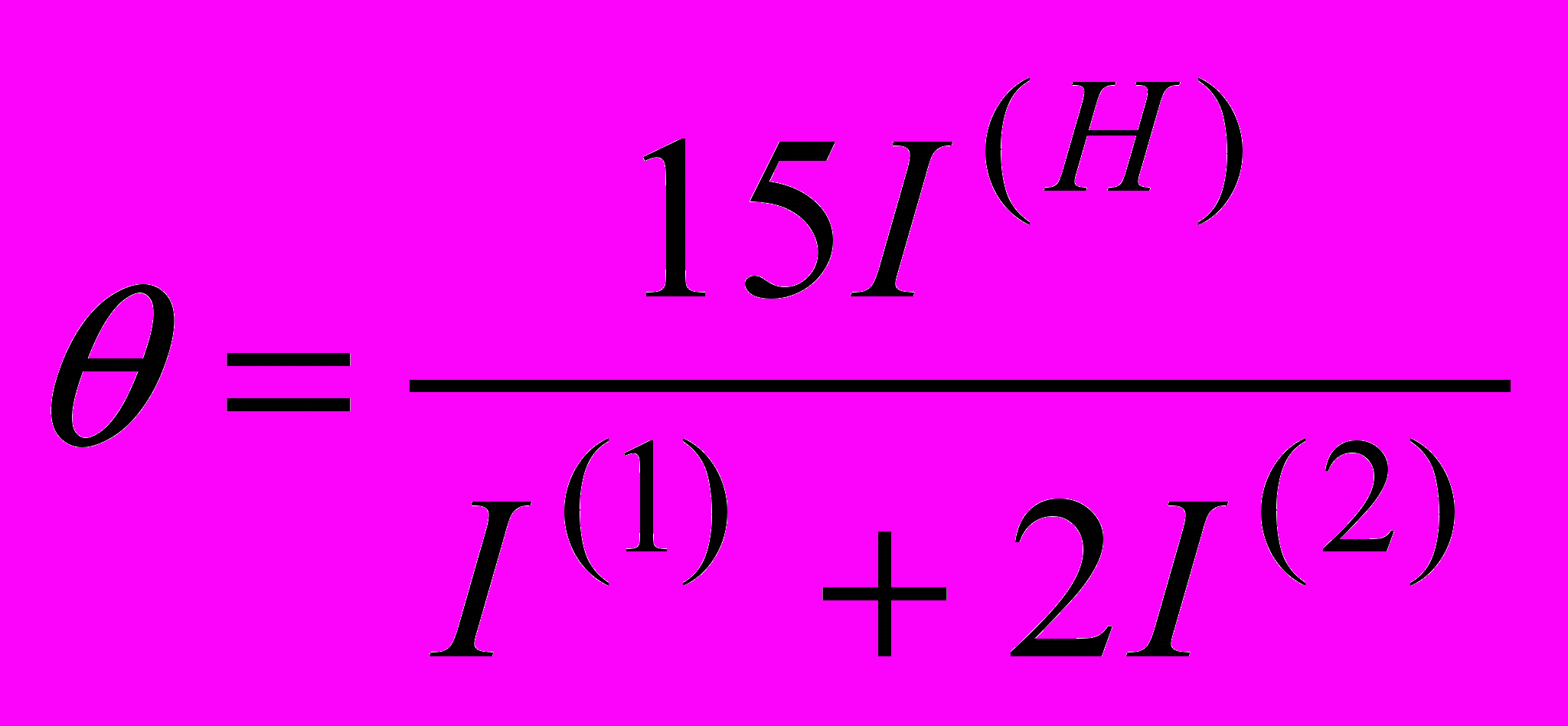 . (11а)
. (11а)Изменение схемы поиска
Эксперименты из [1] показали, что с увеличением числа градаций, старты из более глубокого минимума клиппированного функционала приводят к нахождению более глубокого минимума исходного функционала. Поэтому логично предположить, что достаточно стартовать только из наиболее глубоких минимумов клиппированного функционала. Для подтверждения этого предположения были проведены дополнительные эксперименты, а именно:
а) Производились спуски по клиппированной сети и фиксировались значения энергий клиппированной сети.
б) Определялось среднее значение энергии клиппированной сети, которое разбивало область значений на левую и правую части.
в) Из минимумов клиппированной сети производились спуски по обычной сети Хопфилда.
г) Определялся самый глубокий минимум обычной сети.
д) Определялось, есть ли попадание в самый глубокий минимум из левой и правой областей энергетического спектра клиппированной сети.
На рис. 3 приведены результаты экспериментов для
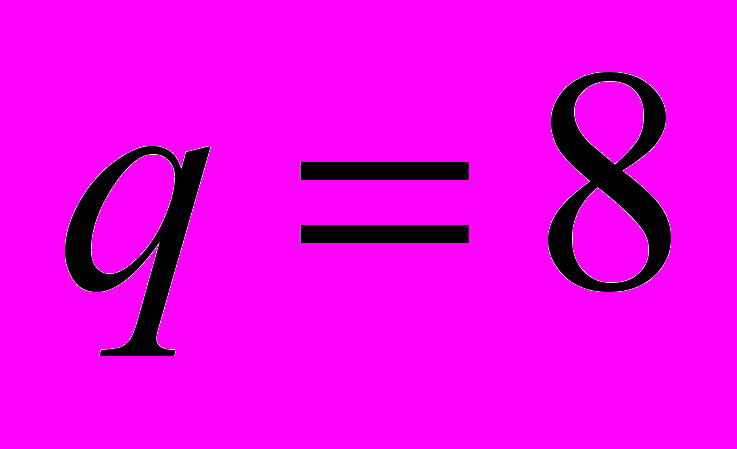 .
.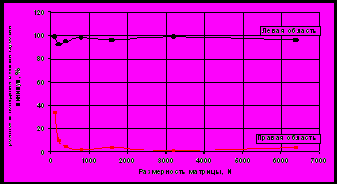
Рис. 3. Вероятность попадания в самый глубокий минимум из левой и правой
областей энергетического спектра клиппированной сети
Видно, что вероятность найти наиболее глубокий минимум хотя бы один раз при стартах из состояний левой области значительно больше, чем при стартах из состояний правой области. Среднее значение этой вероятности 0,96. Это означает, что для нахождения наиболее глубокого минимума спуски из состояний, принадлежащих правой области, малоэффективны, и при поиске достаточно проводить коррекцию состояний из левой области. Это уменьшает объем вычислений в 2 раза. В этом случае формула (11а) приобретает вид
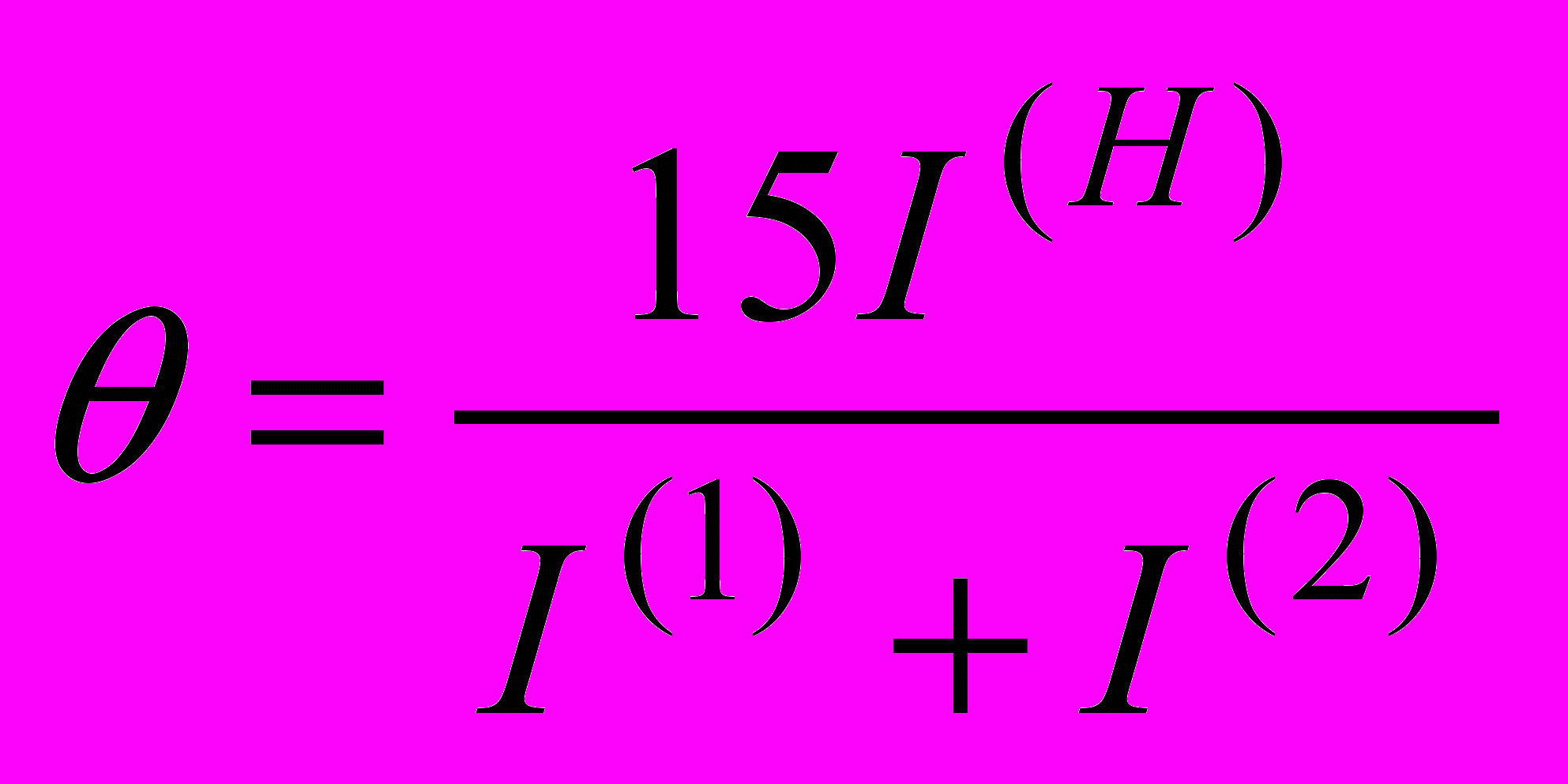 . (11б)
. (11б)Модификация схемы расчета градиента
Можно заметить, что достаточно в самом начале вычислить сумму
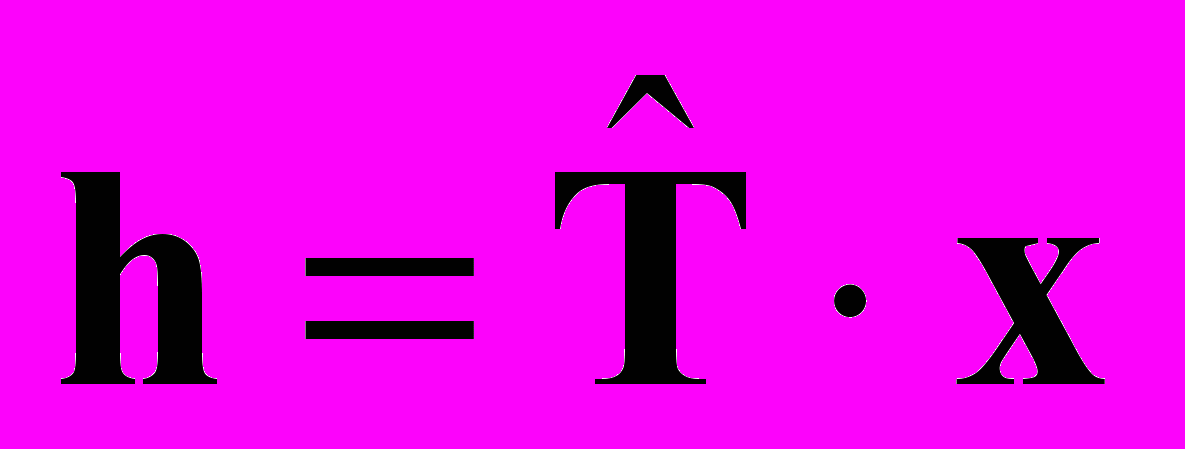 и при каждом изменении
и при каждом изменении 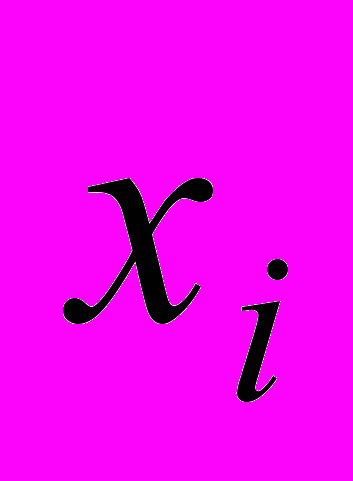 обновлять все компоненты
обновлять все компоненты  по формуле
по формуле . (12)
. (12)Подобная модификация расчета градиента уместна при малом количестве переворачиваемых спинов.
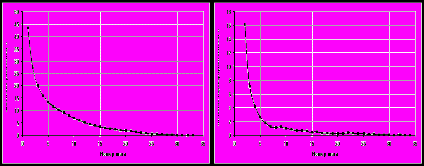
Рис. 4. Изменение расстояния до локального минимума по Хеммингу состояния от номера шага (рисунок слева). Количество изменяемых компонент состояния на каждом шаге (рисунок справа)
На рис. 4 показано, как меняется количество переворачиваемых спинов на каждом шаге (
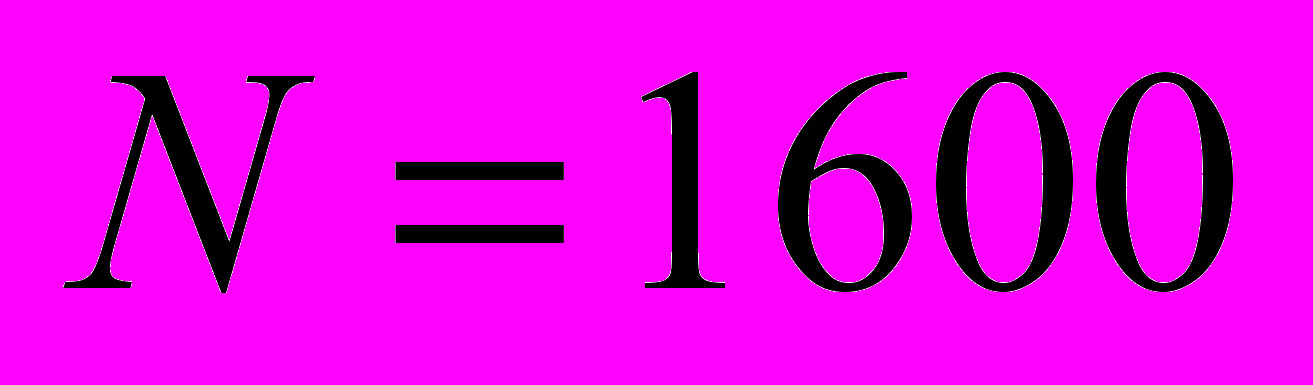 ). Видно, что количество перевернутых спинов уменьшается с каждым шагом и уже на 4-м шаге составляет менее 15% от размерности сети. Поэтому имеет смысл, начиная с 4 – 5 шага, изменить схему расчета градиента и применять обновление по формуле (12).
). Видно, что количество перевернутых спинов уменьшается с каждым шагом и уже на 4-м шаге составляет менее 15% от размерности сети. Поэтому имеет смысл, начиная с 4 – 5 шага, изменить схему расчета градиента и применять обновление по формуле (12).Таблица 2
Ускорение алгоритма при использовании
модифицированной схемы расчета градиента
| Размерность, N | Ускорение, Θ |
| 100 | 5 |
| 200 | 6 |
| 400 | 8 |
| 800 | 10 |
| 1600 | 11 |
| 3200 | 19 |
В табл. 2 показана зависимость ускорения работы сети с модифицированной схемой расчета градиента, по сравнению с обычной, в зависимости от размерности сети. Здесь
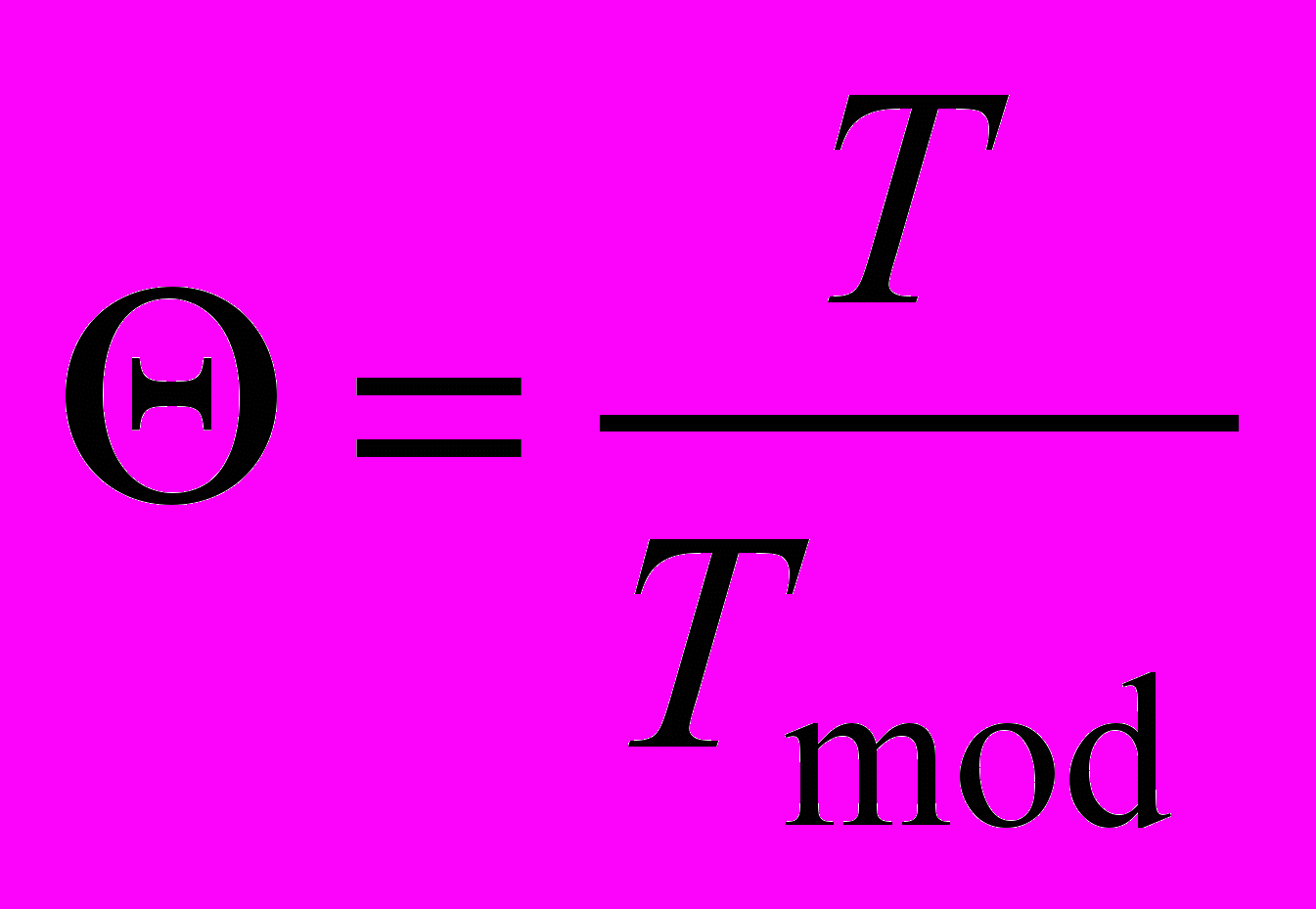 , (12)
, (12)где
 – время работы обычной сети,
– время работы обычной сети,  – время работы модифицированной сети.
– время работы модифицированной сети.Видно, что подобная модификация расчета градиента более, чем в 5 раз уменьшает объем вычислений.
Заключение
Применение описанных в данной статье модификаций работы алгоритма и схем расчета позволяет уменьшить время поиска глобального минимума в 40-50 раз по сравнению с вычислениями, проводимыми с помощью сети Хопфилда.
Список литературы
- Крыжановский М.В., Мальсагов М.Ю. Применение процедуры клиппирования и ее обобщение в задачах поиска глобального минимума // XI Всероссийская научно-техническая конференция «Нейроинформатика-2009». М.: МИФИ, т.2, с. 61, 2009.
1 Работа выполнена при поддержке гранта РФФИ 09-07-00159-а.
УДК 004.032.26(06) Нейронные сети
