Isbn 978-5-7262-1226 нейроинформатика 2010

Вид материала

Документы

Содержание Основы метода конечных элементов Бессеточные методы Метод конечных элементов с применением нейронной сети Сравнительный анализ для экспериментов

Подобный материал:

• Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 136.25kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 9.21kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 113.94kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 124.83kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 86.68kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 101.88kb.
• Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 127.94kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.

Ю.Н. ЗЕМСКОВА

Пензенский государственный педагогический университет им. В. Г. Белинского

zjn21@mail.ru


ПРИМЕНИМОСТЬ КОМПАКТНО ПОДДЕРЖИВАЕМЫХ

НЕЙРОННЫХ СЕТЕЙ ДЛЯ РЕШЕНИЯ

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ

ПРОИЗВОДНЫХ ЭЛЛИПТИЧЕСКОГО ТИПА

МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ¹


В работе рассматриваются численные методы решения дифференциальных уравнений в частных производных (ДУЧП). Предложено использование радиально-базисных нейронных сетей для реализации метода конечных элементов при решении ДУЧП эллиптического типа.


Основы метода конечных элементов


Пусть в области необходимо решить некоторую дифференциальную задачу [1]. Данную область разбивают на подобласти – элементы, которые не пересекаются. В каждом конечном элементе выбирается система нумерованных узлов, в которых значения искомой функции являются неизвестными величинами. Каждому нумерованному узлу приписывается базисная функция, равная единице в нем, а в остальных нумерованных узлах равная нулю. Число базисных функций в расчетной области равно числу нумерованных узлов. Решение искомой дифференциальной задачи строится в виде линейной комбинации базисных функций по всем нумерованным узлам расчетной области с коэффициентами линейной комбинации, равными значениям искомой функции в нумерованных узлах. Это решение подставляется в дифференциальную задачу. Результатом подстановки будет функциональная невязка. С помощью известных методов взвешенных невязок (коллокаций, Галеркина, наименьших квадратов) функциональная невязка минимизируется по всей расчетной области путем приравнивания нулю скалярного произведения функциональной невязки и весовых функций. В результате получается система линейных алгебраических уравнений (СЛАУ) относительно значений искомой функции в нумерованных узлах.


Бессеточные методы


В стандартных численных методах априори требуется информация о межузловой связности, то есть они, по определению, сеточные. Метод конечных элементов и метод конечных объемов – наиболее универсальные в этом семействе всесторонне изученных численных методов. В последнее время появились новые методы, которые аппроксимируют уравнения в частных производных, основываясь только на наборе узлов [2], без знания дополнительной информации о структуре сетки.


Метод конечных элементов с применением нейронной сети


В данной работе предлагается использование радиально-базисных компактно поддерживаемых функций в качестве базисных функций.

Элемент представлен прямоугольником. Он перекрывается соседними прямоугольниками. Для определения элемента необходимы узловая точка – пересечение диагоналей данного прямоугольника (в двумерном случае), его длины сторон. Область решения разбивается на узлы. Вокруг них определяются конечные элементы – прямоугольники. Определяются функции элемента. В данном исследовании используется компактно поддерживаемая радиально-базисная функция [2]

(1)

где rx, ry – область компактной поддержки по оси x, y соответственно, c, d – ширины, – центр радиально-базисной функции.

Ниже приводится формулировка краевой задачи.

В области решается краевая задача

в ; (2)

на , (3)

где L и B – линейные дифференциальные операторы, а p и q – известные функции независимых переменных.

Область разбивается на конечных элементов. Точки разбиения области являются узлами.

Узлы конечных элементов будут центрами радиально-базисных функций , с помощью которых производится аппроксимация функции решения

, (4)

где – веса. Подстановка (1) в (2) и в (3), и последующее возведение (2) и (3) в квадрат даст невязку

(5)

Главная задача – найти веса или коэффициенты линейной комбинации (4), при которых в (5).

Использование компактной поддержки позволяет уменьшить трудоемкость вычислений. Нахождение невязки будет производиться лишь в области поддержки данной функции.

Однако остаётся проблема подбора размера компактной поддержки по отношению к ширине радиально-базисных функций. Данная проблема решается экспериментальным путём.

Как отмечалось выше, в узлах конечных элементов располагаются центры аппроксимирующих функций. В терминах нейросетевой методологии данные центры будут являться нейронами.

Компактно поддерживаемая радиально-базисная нейронная сеть – это сеть, функции нейронов которой есть компактно поддерживаемые радиально-базисные функции.

Точка x, которая удовлетворяет условию , будет входом нейронной сети. Коэффициенты – веса нейронной сети, которые надо найти. Таким образом, получаются компактно-поддерживаемые радиально-базисные нейронные сети.

Для того, чтобы найти веса, можно использовать градиентные алгоритмы обучения нейронной сети [3, 4].

Точки обучающего множества берутся внутри получившихся областей, а также добавляются сами узлы разбиения.


Эксперименты


Метод конечных элементов с применением нейронной сети использовался при решении двумерных задач.

Цель экспериментов – показать исследовать применимость компактно поддерживаемых нейронных сетей для решения дифференциальных уравнений в частных производных методом конечных элементов.

Решалось уравнение



при граничных условиях

.

Аналитическое решение данной задачи имеет вид

.

Область компактной поддержки принималась равной .

По нахождению решения рассчитывалась относительная среднеквадратическая ошибка решения или норма ошибки решения , определяемая следующим образом:

,

где и – соответственно, вычисленное и точное решение в точке , – количество точек, в которых происходило обучение.

Узлы элемента ассоциируются с нейронами. В данной задаче узлы располагаются на одинаковом расстоянии. Число нейронов будет совпадать с числом узлов. В число точек обучающего множества входят также число нейронов-узлов. Остальные обучающие точки, находящиеся между ними, генерируются случайным образом в процессе обучения. Данные точки должны равномерно распределиться по области, то есть внутри каждого элемента будет находиться одинаковое количество обучающих точек. Веса нейронной сети – это коэффициенты разложения в (5).

Находим функционал ошибки

.

Минимизируем его по весам, центрам и ширинам в (1). Минимизация происходит с помощью метода сопряженных градиентов. Чтобы исключить явление переобучения сети, на каждом наборе обучающих точек проводилось 3-5 циклов обучения.

Процесс обучения осуществляется до тех пор, пока функционал ошибки не станет меньше некоторого бесконечно малого значения. Если данное значение не достигнуто, то процесс обучения остановится после выполнения заданного большого количества циклов обучения.

Когда получено решение, то находится среднеквадратичная ошибка между аналитическим решением и полученным , где – заданное значение в i-той точке, – полученное значение в i-той точке, q – количество точек. На основании этого делается вывод об обобщающей способности сети.


Таблица 1


Сравнительный анализ для экспериментов

с различным критерием остановки процесса обучения

(среднеквадратичная ошибка на последней итерации)

Норма ошибки решения	Среднеквадратичная ошибка на последней итерации	Среднеквадратичная ошибка полученного решения и аналитического	Количество итераций
0.0025	0.0000235	0.00000161	35001
0.0023	0.0000121	0.00000141	70001

Область определения разбивалась на десять элементов. Количество обучающих точек 169 в , по 40 на каждой границе. Результаты представлены в табл. 1 и на рис. 1-2 соответственно. Задача решалась на компьютере с процессором Intel(R) Pentium(R) 4 CPU 3.06 GHz 3.07 ГГц, с оперативной памятью – 1.00 ГБ.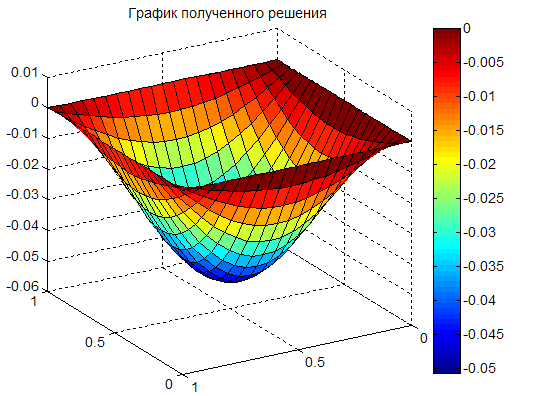





а) б)


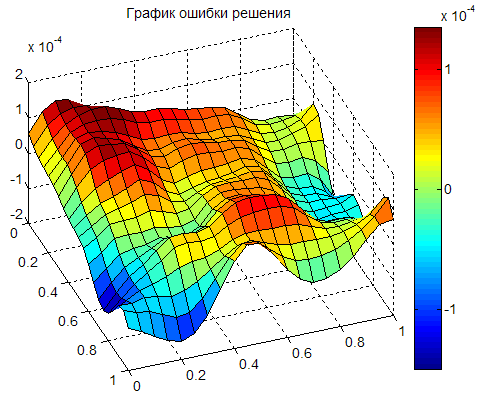
Рис. 1. График полученного решения (а), график разности

между полученным решением и аналитическим (ошибка решения

в контрольных точках, в которых находилось решение) (б)





а) б)


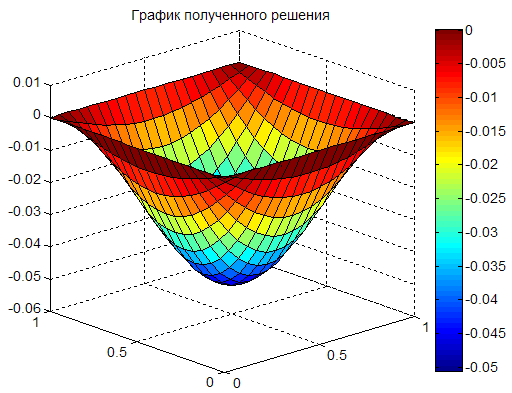
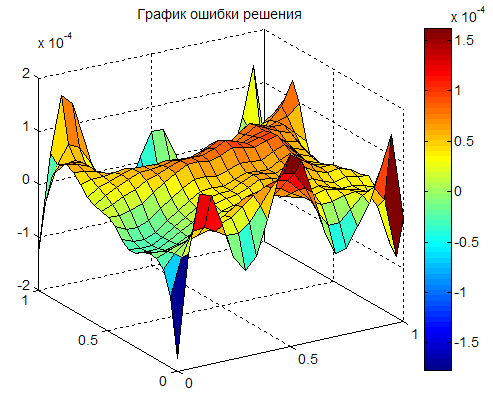
Рис. 2. График полученного решения (а), график разности

между полученным решением и аналитическим (ошибка решения

в контрольных точках, в которых находилось решение) (б)

Как видно из результатов экспериментов, при достаточно большом числе элементов возможно получение относительно точного решения, норма ошибки решения меньше, чем в [5]. Это говорит о работоспособности идеи использования компактно поддерживаемых радиально-базисных нейронных сетей для решения дифференциальных уравнений в частных производных методом конечных элементов и более высокой точности нового метода.


Выводы


Использование радиально-базисных нейронных сетей для реализации метода конечных элементов пригоден для аппроксимации решения ДУЧП в двумерном случае. Он более прост в применении, чем стандартный метод конечных элементов и бессеточные методы, так как не требует формирование СЛАУ, громоздких матричных преобразований матрицы СЛАУ. Однако возможность применения компактно поддерживаемых нейронных сетей для трехмерных задач ещё не исследована.

Из выше сказанного следует, что данный метод отличается от метода конечного элемента, так как функцию элемента формируют для конкретного узла.

Существующий бессеточный метод (Канса) [5] с нейронной сетью отличается тем, что в данном методе всё-таки присутствует элемент. В то время как декомпозиция Канса полностью лишена его.

По сравнению с последним бессеточный метод конечных элементов на нейронной сети обладает преимуществом вычислительного характера, так как отсутствует необходимость нахождения значений всех функций-аппроксиматоров в данной точке. В то же время обучение позволяет подогнать аппроксимацию с нужной точностью.

Остальные бессеточные методы аппарат нейронных сетей не используют.


Список литературы

1. Формалёв В. Ф. Численные методы / В. Ф. Формалёв, Д. Л. Ревиз­ников – М.: ФИЗМАТЛИТ, 2004. 400 с.
   
2. Fries, T.-P. Classification and Overview of Meshfree Methods/ T. P. Fries, H.-G. Matthies // Institute of Scientific Computing Technical University Braunschweig Brunswick, Germany, 2004. Р. 64.
   
3. Осовский С. Нейронные сети для обработки информации. М.: Финансы и статистика, 2002. 344 с.
   
4. Хайкин С. Нейронные сети: полный курс. М.: Изд. дом «Вильямс», 2006. 1104 с.
   
5. Jianyu L., Luo S, Yingjian Q., Yaping H. Numerical solution of elliptic partial differential equation using radial basis function neural networks / Neural Networks. V.16. №5-6. 2003. P. 729-734.