Isbn 978-5-7262-1377 нейроинформатика 2011

Вид материала

Документы

Содержание Ключевые слова Постановка задачи Схема метода I, отличаются тем, что значения первых из них задаются пользователем до решения задачи t Программная реализация метода Исследование эффективности метода

Подобный материал:

• Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
• Isbn 978-5-7262-1377 нейроинформатика 2011, 143.59kb.
• Isbn 978-5-7262-1377 нейроинформатика 2011, 97.16kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 127.94kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 105.62kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
• Isbn 978-5-7262-1376 нейроинформатика 2011, 103.58kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 79.42kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 136.25kb.

А.П. КАРПЕНКО, З.О. СВИАНАДЗЕ

Московский государственный технический университет им. Н.Э.Баумана

apkarpenko@mail.ru


МЕТА-ОПТИМИЗАЦИЯ НА ОСНОВЕ

САМООРГАНИЗУЮЩИХСЯ КАРТ КОХОНЕНА

И ГЕНЕТИЧЕСКОГО АЛГОРИТМА


Рассматривается задача параметрической оптимизации алгоритмов поисковой оптимизации (задача мета-оптимизации). Предложен метод мета-оптимизации, основная особенность которого заключается в отыскании оптимальной стратегии алгоритма в процессе нормальной эксплуатации реализующей его программы. Метод использует кластеризацию множества задач рассматриваемого класса с помощью самоорганизующихся карт Кохонена и решение собственно задачи мета-оптимизации с помощью непрерывного генетического алгоритма.


Ключевые слова: мета-оптимизация, самоорганизующаяся карта Кохонена (SOM), непрерывный генетический алгоритм


Введение


В современных алгоритмах поисковой оптимизации обычно имеется значительное число свободных параметров, вектор значений которых называется стратегией алгоритма. Стратегия алгоритма оптимизации в значительной степени определяет его эффективность. Поэтому возникает задача поиска оптимальной стратегии алгоритма. Эта задача называется задачей мета-оптимизации. Оптимизируемый алгоритм и соответствующая программа называются базовыми, а алгоритм и программа решения задачи мета-оптимизации – мета-алгоритмом и мета-программой.

Известен ряд работ, посвященных теоретическому анализу влияния различных стратегий на эффективность некоторых базовых алгоритмов. Однако исследования такого сорта основаны на сильных упрощениях базового алгоритма и имеют ограниченную практическую ценность. Обычно задачу мета-оптимизации решают численными методами, которые можно разделить на две группы – методы управление параметрами и методы настройки параметров [Michalewicz Z., Hinterding R., Eiben A.E. Parameter Selection. Evolutionary Optimization. New York: Springer. 2003. V. 48. № 11. P. 279–306.].

В методах настройки параметров задача мета-оптимизации решается для некоторого класса задач. Найденные оптимальные стратегии базового алгоритма фиксируются и используются для решения других задач данного класса. Методы настройки параметров разделяются на методы однократной настройки и методы перманентной настройки [1].

В методах управления параметрами задача мета-оптимизации решается в процессе решения исходной задачи оптимизации (с помощью базового алгоритма). Основная идея состоит в том, что поскольку для каждой задачи оптимизации оптимальной является, вообще говоря, своя стратегия, поиск этой стратегии необходимо производить в процессе каждого запуска базового алгоритма. Методы управления параметрами разделяются на методы адаптивного управления и методы само-адаптивного управления [1].

В данной работе предлагается вариант метода мета-оптимизации на основе перманентной настройки, основная особенность которого состоит в отыскании оптимальной стратегии базового алгоритма в процессе нормальной эксплуатации соответствующей базовой программы, т.е. в процессе решения не тестовых, а реальных задач оптимизации. При этом базовая программа перед началом вычислений посылает мета-программе априорную информацию об атрибутах решаемой задачи, а после завершения вычислений – апостериорную информацию о тех же атрибутах. Программная реализация метода приводит к распределенной мета-программной системе, центральная часть которой в процессе своего функционирования накапливает информацию об атрибутах задач, когда-либо решавшихся в системе. При предъявлении системе базовой программой априорных значений атрибутов новой задачи, система на основе накопленной информации возвращает базовой программе приближенно-оптимальную стратегию базового алгоритма.


Постановка задачи


Рассмотрим задачу глобальной безусловной оптимизации

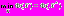, (1)

где 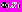– скалярная целевая функция, 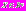– n-мерный вектор варьируемых параметров, – искомый оптимальный вектор варьируемых параметров. Рассматриваемый класс задач вида (1) обозначим 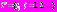, где 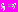одна из задач этого класса.

Пусть – базовый алгоритм решения задач класса , где 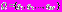– стратегия этого алгоритма. Положим, что для каждого из компонентов стратегии Q заданы интервалы его допустимых значений 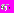так что определено множество 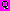допустимых стратегий

,

которое определяет множество алгоритмов

.

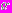Задача 1. Для задачи найти стратегию (а тем самым, и алгоритм 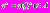), которая обеспечивает минимальное значение критерия оптимальности алгоритма :

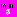
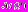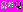=, . (2)

Можно предложить целый ряд критериев , отражающих разные аспекты представлений лица, принимающего решения, об оптимальности стратегии Поэтому задача (2) рассматривается как многокритериальная задача с частными критериями оптимальности , . В качестве этих критериев могут быть использованы, например, оценка времени решения задачи с помощью алгоритма , оценка вычислительных затрат на решение собственно задачи мета-оптимизации (2) и т.д.

Положим, что тем или иным способом, например, с помощью аддитивной скалярной сверки [Черноруцкий И.Г. Методы принятия решений. СПб.: БХВ-Петербург. 2005. 416 с.] векторный критерий оптимальности 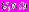, 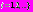приведен к скалярному критерию .

Задача 2. Для класса задач найти стратегию (а тем самым и алгоритм ), которая обеспечивает минимальное значение критерия оптимальности :

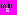
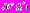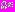
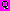=, . (3)

В данном случае также можно предложить вектор критериев оптимальности и задачу следует рассматривать, как задачу многокритериальной оптимизации. Положим, что аналогично задаче 1 векторный критерий оптимальности приведен к скалярному критерию .

Схема метода


Введем в рассмотрение вектор атрибутов задачи , примерами которых могут служить константа Липшица функции (если функция является липшицевой), максимальное значение градиента этой функции (если она дифференцируема), число локальных минимумов той же функции, требуемая точность решения задачи, вычислительная сложности функции и т. д. Совокупность всех возможных значений вектора 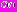, обозначим .

Выделим среди атрибутов 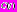задачи ее априорные 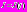и апостериорные 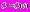атрибуты. Атрибуты I, отличаются тем, что значения первых из них задаются пользователем до решения задачи t, а значения вторых – определяются базовой программой в процессе решения этой задачи. Отметим, что некоторые из атрибутов могут до решения задачи принадлежать к априорным атрибутам, а после решения задачи – становиться апостериорными атрибутами. Вместо 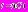, будем далее писать .

Основная идея метода состоит в следующем:

- в процессе нормальной эксплуатации базовой программы (т.е. в процессе решения задач класса T) формируется и непрерывно пополняется множество ;

- производится сначала кластеризация, а затем периодическая рекластеризация этого множества – выделяется кластеры , ;

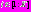- каждому из кластеров ставится в соответствие стратегия ;

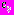- для задачи среди кластеров выбирается кластер , которому принадлежат значения ее априорных атрибутов ;

- соответствующая стратегия 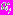по некоторому правилу варьируется и полагается оптимальной стратегий базового алгоритма для задачи .

Метод требует решения двух следующих основных задач:

- задача кластеризации множества ;

- задача оптимизации стратегий (т.е. собственно задача мета-оптимизации).


Программная реализация метода


Программная реализация метода имеет клиент-серверную архитектуру, которая позволяет перенести вычислительные затраты, связанные с мета-оптимизаций, на сервер приложений. Используется трехзвенная архитектура, включающая в себя рабочие станции, сервер приложений и сервер баз данных. Такая архитектура обеспечивает хорошую масштабируемость системы, малую дополнительную нагрузку на рабочие станции клиентов, надежность и высокую безопасность данных.

После задания пользователем значений априорных атрибутов решаемой задачи t, клиентская и серверная части программного обеспечения выполняют следующие основные действия:

- клиентская программа посылает серверной программе вектор ;

- получив этот вектор, серверная программа определяет кластер , которому принадлежит вектор , выбирает соответствующую этому кластеру стратегию 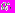варьирует ее и отсылает полученную стратегию клиентской программе;

- клиентская программа, получив стратегию 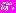запускает процесс решения задачи t с помощью алгоритма ;

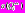- завершив решение задачи t, клиентская программа формирует вектор 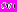значений апостериорных атрибутов этой задачи и отсылает его серверной программе;

- получив вектор 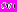, серверная программа фиксирует его в своей базе данных.

Вектор атрибутов задачи полагается трехмерным 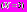и включает в себя следующие атрибуты:

-  – константа Липшица функции ;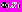

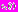-  – количество локальных минимумов функции ;

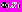-  – требуемая точность решения задачи.

В качестве критерия оптимальности используется время решения задачи с помощью алгоритма ; в качестве критерия оптимальности алгоритма на классе функций T – критерий

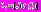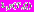++. (4)

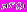Здесь , – символы оценок математического ожидания и среднего квадратичного отклонения критерия на классе задач T; – оценка вероятности локализации минимума функции на классе задач T; – веса соответствующих частных критериев оптимальности.

Для решения задачи кластеризации множества реализован высокоэффективный алгоритм на основе самоорганизующихся карт Кохонена (Self-OrganizingMap – SOM) [Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. М.: Мир. 1992. 240 с.]. Серверная программа поддерживает периодическую рекластеризацию множества с увеличением его мощности. На начальном этапе функционирования системы, когда мощность этого множества мала, используется только один кластер. С ростом мощности множества число кластеров увеличивается. Поскольку каждое увеличение числа кластеров требует значительных вычислительных затрат на переобучение нейронной сети, реализующей карту Кохонена, интервал между переобучениями возрастает.

Решение задачи оптимизации стратегии реализовано с помощью непрерывного генетического алгоритма, использующего улучшенный бинарный кроссовер SBX (Simulated Binary Crossover), имитирующий классический бинарный кроссовер. Отметим, что сила поиска (search power) кроссовера SBX равна силе поиска классического одноточечного двоичного кроссовера [Deb K., Kumar A. Real coded genetic algorithms with simulated binary crossover: Studies on multi modal and multi objective problems // Complex Systems. 1995. V. 6. № 9, P. 431–454.]. Для каждого из кластеров создается своя популяция генетического алгоритма. В качестве функции приспособленности индивидов во всех случаях используется аддитивная свертка частных критериев оптимальности (4). Реализована неравномерная мутация [roup.ru/library/optimization/real_coded_ga/].


Исследование эффективности метода


В качестве базового алгоритма a рассмотрен алгоритм метода Нелдера-Мида (метода деформируемого многогранника), относящийся к классу прямых детерминированных методов оптимизации [Nelder J.A., Mead R. A simplex method for function minimization // The Computer Journal. 1965. V. 7. P. 308–313.]. В качестве свободных параметров алгоритма рассмотрены параметры 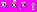– коэффициенты отражения, редукции, сжатия и растяжения соответственно. Таким образом, и стратегия алгоритма задается вектором , где , , , 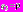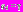. Множество допустимых стратегий имеет вид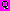

,

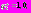
где Обозначим стратегию алгоритма Нелдера-Мида, рекомендованную в работе [Nelder J.A., Mead R. A simplex method for function minimization // The Computer Journal. 1965. V. 7. P. 308–313.], и назовем ее рекомендованной стратегией.

Класс задач построен на основе совокупности следующих восьми тестовых функций [Tang K., Yao X., Suganthan P.N. et al. Benchmark functions for the cec’2008 special session and competition on large scale global optimization // Tech. rep. / Nature Inspired Computation and Applications Laboratory, USTC, China, 2007.]: двумерная функция Химмельблау; двумерная функция Розенброка; двумерная функция Шафера; трехмерная функция сфера; пятимерная функция Step; многомерная функция Экли; многомерная функция Растригина; многомерная функция Шекеля. Говоря более строго, класс задач T образуют указанные функции, свободные параметры которых представляют собой случайные числа, равномерно распределенные в некоторых интервалах.

Приведенные ниже результаты получены на основе решения более 150 тысяч задач указанного класса T. Число кластеров , выделенных во множестве С, к моменту завершения исследования достигло .

Динамику развития одного из кластеров иллюстрирует рис. 1. Рисунок показывает, что с ростом числа популяций r значение критерия оптимальности 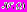быстро уменьшается, т.е. генетический алгоритм мета-оптимизации для данного кластера быстро находит стратегию, близкую к оптимальной.

Поскольку алгоритм мета-оптимизации создает начальные стратегии случайным образом, в начале развития кластеров для решения задачи в среднем требуется число испытаний большее, чем базовому алгоритму со стратегией [6]. Аналогично, в начале развития кластеров меньше вероятность локализации минимума функций 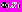. Ситуация изменяется на противоположную всего после нескольких поколений генетического алгоритма мета-оптимизации.

Спустя 30 поколений развития кластеров было выполнено исследование эффективности найденных оптимальных стратегий Интегральные результаты исследования иллюстрирует табл. 1. Для сравнения в таблице приведены также результаты, полученные для рекомендованной стратегии Алгоритмы 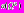запускались из одних и тех же начальных точек и с одинаковой требуемой точностью решения.



Рис. 1. К динамике развития кластеров


Таблица 1

Результаты исследования оптимальных стратегий

Число испытаний	Стратегия	Стратегия
Среднее	161	130
Минимальное	35	16
Максимальное	600	600

Табл. 1 показывает, что средняя производительность алгоритма Нелдера-Мида при использовании стратегий выше производительности при использовании рекомендованной стратегии на 24 %.

Кроме того, спустя то же число поколений развития кластеров было проведено исследование эффективности лучших стратегий этих кластеров (табл. 2). Исследование выполнено на 100 функциях, случайно выбранных из множества функций T.

Таблица 2

Результаты исследования лучших стратегий

Число испытаний	Стратегия	Стратегия
Среднее	214	115
Минимальное	24	13
Максимальное	1000	350

Табл. 2 показывает, что стратегии, найденные мета-алгоритмом, обеспечивают по сравнению с рекомендованной стратегией значительно более высокую производительность: в среднем стратегии на 19 % эффективнее стратегии ; в лучшем случае, стратегия на 46 % эффективнее стратегии

Выводы


В работе предложен метод мета-оптимизации базового алгоритма оптимизации в процессе нормальной эксплуатации соответствующей базовой программы. Выполнена программная реализация метода, имеющая трехзвенную клиент-серверную архитектуру. Экспериментальное исследование эффективности метода выполнено на примере мета-оптимизации алгоритма Нелдера-Мида, как базового алгоритма. Результаты исследования показывают перспективность предложенного метода, а также эффективность использования в нем самоорганизующихся карт Кохонена и непрерывного генетического алгоритма .

Клиент-серверная архитектура разработанного программного обеспечения метода вносит в систему накладные расходы, обусловленные коммуникациями между его клиентской и серверной частями. Для задач, имеющих невысокую вычислительную сложность, это обстоятельство может приводить к неэффективности мета-оптимизации, поскольку выигрыш в количестве испытаний может быть перевешен накладными расходами. Однако в задачах, представляющих практический интерес, типичной является высокая вычислительная сложность целевой функции, обеспечивающая малый удельный вес указанных коммуникационных расходов. Как следует из результатов исследования, в такой ситуации мета-оптимизация базового алгоритма оптимизации может обеспечить значительный положительный эффект.

В работе в качестве исходной задачи оптимизации рассмотрена задача многомерной глобальной безусловной оптимизации. Для решения задач условной оптимизации в вычислительной практике широко используются методы штрафных и барьерных функций, сводящие задачу условной оптимизации к совокупности задач безусловной оптимизации [Черноруцкий И.Г. Методы принятия решений. СПб.: БХВ-Петербург. 2005. 416 с.]. Таким образом, полученные в работе результаты могут быть использованы и при глобальной условной оптимизации.

С другой стороны, имеется большое число методов решения задач глобальной условной оптимизации, которые не используют сведение ее к задаче безусловной оптимизации. Это обстоятельство делает актуальной модификацию предложенного в работе метода и программного обеспечения для решения задач глобальной условной оптимизации, как самостоятельного класса задач.

Как отмечалось выше, задача мета-оптимизации представляет собой, по сути, задачу многокритериальной оптимизации. В работе для решения этой задачи использован простейший метод решения многокритериальных задач – метод сведения их с помощью аддитивной скалярной свертки к однокритериальным задачам. Представляется перспективной модификация предложенного в работе метода и программного обеспечения, использующая более тонкие методы решения задач многокритериальной оптимизации.

Список литературы

1. Michalewicz Z., Hinterding R., Eiben A.E. Parameter Selection. Evolutionary Optimization. New York: Springer. 2003. V. 48. № 11. P. 279–306.
   
2. Черноруцкий И.Г. Методы принятия решений. СПб.: БХВ-Петербург. 2005. 416 с.
   
3. Уоссермен Ф. ссылка скрыта. М.: Мир. 1992. 240 с.
   
4. Deb K., Kumar A. Real coded genetic algorithms with simulated binary crossover: Studies on multi modal and multi objective problems // Complex Systems. 1995. V. 6. № 9, P. 431–454.
   
5. ссылка скрыта
   
6. Nelder J.A., Mead R. A simplex method for function minimization // The Computer Journal. 1965. V. 7. P. 308–313.
   
7. Tang K., Yao X., Suganthan P.N. et al. Benchmark functions for the cec’2008 special session and competition on large scale global optimization // Tech. rep. / Nature Inspired Computation and Applications Laboratory, USTC, China, 2007.