Geum.ru

Лекция 3

Вид материалаЛекция

Содержание


R , С и электрическим ключом.
RС/2 значение напряжения на ёмкости после первой коммутации можно разложить по малому параметру |рt| «1, и тогда U
Подобный материал:
Лекция 3.

Сигналы произвольной формы. Разложение по гармоникам. Нелинейности реальных элементов – источники гармоник. Фактор мощности. Квазипрямоугольный сигнал - его измерение и идеальная форма. Переходные процессы. Новый аналоговый элемент - электрический ключ. Классический метод решения в простых линейных цепях (до второго порядка). Интегрирующие и дифференцирующие цепи. Переходные характеристики.


Если в силовой электротехнике превалирует одна частота, на которой работают мощные электромеханические генераторы, то в электронике, напротив, мы имеем дело, как правило, с сигналом произвольной формы. Здесь приведён ещё самый понятный сигнал последовательности прямоугольных импульсов, которые используют в цифровой технике для передачи битов информации.




Сигналы произвольной формы можно разложить в тригонометрический ряд Фурье, который в простейшем виде можно представить как сумму гармонических колебаний с частотами, кратными основной частоте сигнала (гармоники)

F(t)=Akejkt , здесь к - действительное число от 1 до .

Ниже приведено разложение по гармоникам данного сигнала (выведено только 20 первых нечётных гармоник).



Эти гармоники возникают при наличии в цепи нелинейных элементов, либо неучтённых нелинейностей выбранных компонентов.

В качестве иллюстрации посмотрим как появляются гармоники в обычной схеме выпрямления напряжения через такой нелинейный элемент как полупроводниковый диод, у которого меняется значение сопротивления в зависимости от направления протекающего тока.



В качестве источника выбран источник гармонического сигнала с амплитудой 100В.

У него одна основная гармоника 50 Гц


Однако диод существенно меняет форму напряжения и тока в нагрузке.




При разложении в ряд Фурье сигналов тока в контуре и напряжения на нагрузке появляются новые гармоники. Во-первых, как и следует, появляется постоянная составляющая на уровне 30В (максимальное напряжение источника 100В). Во-вторых, осталась весьма существенная основная гармоника (около 45 В) и видны новые 2, 3, 4 и 5 гармоники.






Самое неприятное в том, что токовые гармоники проходят в источник!!! Это приводит к передаче существенной части энергии на гармониках, что очень не любят в силовой электротехнике, поскольку это приводит к уменьшению отношения активной энергии Р, переданной в нагрузку (двигатель), к полной мощности S, проходящей по системе. То есть, как уже говорили, к уменьшению коэффициента или фактора мощности.

Но что плохо для «электриков», то хорошо для «электронщиков», а «цифровики» вообще без прямоугольного импульса не могут обойтись.

Основным поставщиком гармоник с математической точки зрения является единичная функция (прямоугольный импульс образуется применением двух единичных функций).





И это только первые 100 гармоник.

Применение комплексного метода к моделированию цепей с сигналами произвольной формы возможно, если решать системы уравнений для каждой гармоники в отдельности и результат потом складывать. Практически это делают только для основной гармоники (приближение по основной гармонике). Естественно, полученный результат будет иметь погрешность 100%. А при наличии в цепи нелинейности, генерирующей единичную функцию, такой метод анализа электрической цепи вообще неприменим, так как там бесконечное количество гармоник.


Устройство в цепи, которое генерирует единичную функцию, называют электрическим ключом. Его прообразом и первым реальным исполнением является электрический рубильник, который переводит нагрузку из одного энергетического состояния в другое. В настоящее время разработаны самые разнообразные электрические ключи от реле до полевых транзисторов с использованием самых различных нелинейных эффектов. Поэтому в дальнейшем при моделировании электрических цепей мы будем пользоваться идеальным электрическим ключом, сопротивление которого изменяется от 0 до  за бесконечно малый промежуток времени. Соответственно,

Нормально-открытый ключ, включатель (НО, switch on)

R(t)= {, при tT0

{0, при tT0





Нормально-замкнутый ключ, выключатель (НЗ, switch off)

R(t)= {0, при tT0

{, при tT0


Проведём моделирование классическим методом простейших схем с электрическим ключом.

Схема с R , С и электрическим ключом.




Нормальное положение ключа – разомкнут.

После момента первой коммутации ключ переходит в замкнутое положение и имеет пренебрежимо малое сопротивление, но временные зависимости тока и напряжения на элементах неизвестны, т.к. в этот момент все временные функции имеют математический разрыв.

Сшить решения в этой точке нам помогают правила коммутации, которые вытекают из законов сохранения заряда и магнитного потока. Они гласят, что напряжение на ёмкости и ток в индуктивности при коммутации сохраняются. Чтобы нарушить эти правила, нужно обеспечить бесконечно большие мощности при передаче электромагнитной энергии, что невозможно (по крайней мере в нашей Галактике) из-за ограничения скорости света.

Итак, IL = IL+ и UC- =UC+ .


Напишем уравнение для данной цепи после первой коммутации по 1 правилу Кирхгофа при неизвестной временной зависимости напряжения на ёмкости после коммутации.

Учитывая, что IC=CdUC/dt и UC= (2-0), а также заменяя источник э.д.с. Е с внутренним сопротивлением R1 на источник тока Е/R1 с таким же внутренним сопротивлением, получим

Е/R1= UC/R1 + UC/R2 + CdUC/dt = UC (R1+R2/R1R2) + CdUC/dt

или

E(R2/R1+R2)= UC + C(R1R2/R1+R2)  dUC/dt

При R1=R2=R

UC+0,5RСdUC/dt = Е/2

Это линейное дифференциальное уравнение первого порядка с правой частью. Его решение будем искать как сумму общего решения однородного уравнения UC0 без правой части (свободные токи и напряжения) и одного из частных решений неоднородного уравнения, UУ (установившиеся токи и напряжения).

UC= UC0+ UУ

Свободные параметры найдём из уравнения UC+0,5RСdUC/dt = 0 в виде UC0=Аеpt.

До момента первой коммутации (включение): I=0, UC=0, Е=20B.

Классический метод заключается в отдельном поиске неизвестных величин р, UУ и А.

1) Находим р. После подстановки искомой формы решения в уравнение получаем характеристическое уравнение 1+ рRС/2=0. Отсюда р = 2/RС. При t = RC/2 показатель экспоненты равен -1. То есть в грубом приближении искомый параметр снижается втрое. Это даёт возможность говорить об этой величине времени как о характерном времени переходного процесса. Для наших данных характерное время составляет 5 мкс.

Обратите внимание на то, что величина р – отрицательна и действительна. Это показывает на затухающий характер переходных процессов.


Многие делают ошибку, вспоминая j из гармонического анализа вместо р. В действительности область значений частот р, как неизвестной величины, бесконечна, и включает как действительные числа, так и мнимые, как например j.

  1. Найдём установившееся значение UУ при значении времени t   . В это время все переходные процессы завершатся (они затухающие). И так как у нас источник постоянного тока, то и цепь можно рассматривать в приближении постоянного сигнала. По правилу делителя напряжения UУ = Е/2.
  2. Найдём значение А при t = 0. Для этого воспользуемся правилом коммутации для ёмкости, UС= UС+ = 0. Тогда Аеp0+E/2=0 или А+E/2=0 или А = Е/2.

Полное решение UС =0,5Еерt+0,5Е=0,5Е(1 ерt), где р = 2/RС.

Ток через конденсатор можно найти из соотношения

IС= СdUC/dt =С2Еерt/ 2RС= (Е/R)ерt

Можно показать, что энергия заряженного конденсатора равна активной энергии, выделяемой на зарядном резисторе R1 (при R2 ).

Для данных конкретной схемы эти функции выглядят следующим образом.




Таким образом, можно сказать, что конденсатор в начале переходного процесса ведёт себя как короткозамыкающая перемычка. То есть все старшие гармоники замыкаются на конденсаторе. Оно и понятно: чем выше частота, тем меньше реактанс конденсатора. Поэтому ток в начале заряда конденсатора ограничивается только резистором в цепи!

После второй коммутации ключ возвращается в разомкнутое (замкнутое) состояние и имеет очень высокое (малое) сопротивление и энергия заряженного конденсатора разряжается через резистор R2.

Уравнение этой цепи по 2 закону Кирхгофа

UC + R2CdUC/dt =0

Отсюда 1 + R2Cр =0 и р=1/R2C. Характерное время процесса 10 мкс.

Установившееся значение UУ= 0.

В момент второй коммутации τ напряжение UC= UC+=0,5Е(1 ерτ)=А.

Отсюда UC=0,5Е(1 ерτ) ер(tτ) , где р=1/R2C

Ток через конденсатор можно найти из соотношения

IС= СdUC/dt =  Е(1 ерτ) ер(tτ)/ 2R2


Графики этих функций представлены на следующем рисунке.




При τ » RС/2=1/р напряжение на ёмкости перед второй коммутацией достигает значения Е/2 и мы получим вместо прямоугольного импульса квазипрямоугольный. Ток через конденсатор имеет переменный характер, что не рекомендуется, например, для электролитических конденсаторов.

При τ « RС/2 значение напряжения на ёмкости после первой коммутации можно разложить по малому параметру |рt| «1, и тогда

UC=0,5Е(1 ер(tτ))=0,5Е(11+ р(tτ))= 0,5Ер( tτ)

То есть мы получаем интеграл от постоянного напряжения источника. Поэтому подобные RC-цепи получили название интегрирующих цепочек.

Если переставить местам резистор R1 и емкость, то на резисторе появится напряжение только старших гармоник, то есть мы получим операцию дифференциирования.

Таким образом с помощью аналоговых элементов можно выполнять все основные математические операции. Это дало возможность создания аналоговых вычислительных машин, которые в настоящее время практически вытеснены цифровой техникой.



На практике очень удобно характеризовать реакции различных электрических цепей на воздействие единичным импульсом так называемыми переходными (импульсными) характеристиками, а именно, отношением амплитуды реакции схемы к амплитуде импульсного воздействия. В рассматриваемой схеме могут быть получены 3 переходных характеристики:
  1. h(t) = UC/E=0,5(1 ерt) или 0,5(1 ерτ) ерt , переходная характеристика по напряжению;
  2. r(t) = (1/R)ерt или  Е(1 ерτ) ер(tτ)/ 2R2 , переходное сопротивление;
  3. g(t)=1/ r(t), переходная проводимость.


Схема с L , R и электрическим ключом.




До момента коммутации I=0, UL=0, Е=10B.

Напишем уравнение для данной цепи после первой коммутации по 1 закону Кирхгофа

при неизвестной временной зависимости тока через индуктивность после коммутации. Выбор в качестве неизвестного параметра тока индуктивности вызван тем, что у нас для него написано правило коммутации.

Учитывая, что UL=LdIL/dt и UL= (2-0), а также заменяя источник э.д.с. Е с внутренним сопротивлением R1 на источник тока Е/R1 с таким же внутренним сопротивлением, получим

E/R1=UL/R1+ UL/R2+IL= UL(1/R1+ 1/R2)+IL= L(1/R1+ 1/R2)dI/dt+IL

При равенстве R1=R2 =R получим E/R= 2L/RdI/dt+IL


Применяем классический метод.
  1. Характеристическое уравнение 2рL/R+1 = 0 . Отсюда р= R/2L
  2. Установившееся значение ILу при t   равно IУ=E/R
  3. Правило коммутации для тока IL = IL+ =0. Отсюда А + E/R=0 и А= E/R

Общее решение IL=E/R(1ept) , где р=  R/2L.

Переходная проводимость g(t)= 1/R(1ept)

Характерное время процесса 1/р= 2L /R , в нашем случае 4 мкс.

Напряжение на индуктивности можно найти из соотношения

UL= LdI/dt =LЕ/R(1-ерt)= LЕ/R(R/2L) ерt= Е/2 ерt

Переходная функция по напряжению h(t)= 1/2 ерt

Для данных конкретной схемы эта функция выглядит следующим образом.





Таким образом, можно сказать, что индуктивность в начале переходного процесса ведёт себя как разрыв в цепи. То есть проходят только младшие гармоники. Оно и понятно: чем выше частота, тем больше реактанс индуктивности. Поэтому на индуктивности в начале переходного процесса падает практически всё напряжение источника (при R2 )!

После второй коммутации ключ возвращается в разомкнутое (замкнутое) состояние и имеет очень высокое (малое) сопротивление и магнитная энергия индуктивности разряжается через резистор R2.

Уравнение этой цепи по 2 закону Кирхгофа

RIL + LdIL/dt =0

Отсюда R + Lр =0 и р=R/L.

Установившееся значение IL= 0.

В момент второй коммутации τ ток IL= IL+=Е/R(1 ерτ)=А.

Отсюда IL=Е/R(1 ерτ) ер(tτ) , где р=R/L

Переходная проводимость g(t)= 1/R(1 ерτ) ер(tτ)

Напряжение на индуктивности можно найти из соотношения

UL= LdIL/dt =  LЕ/R(1 ерτ) ер(tτ)R/L =  Е(1 ерτ) ер(tτ)

Переходная функция по напряжению h(t)= (ерτ1) ер(tτ)

Графики этих функций представлены на следующем рисунке.

Их вид аналогичен тем кривым, что мы получали при работе с ёмкостью, только напряжение и ток поменялись местами.




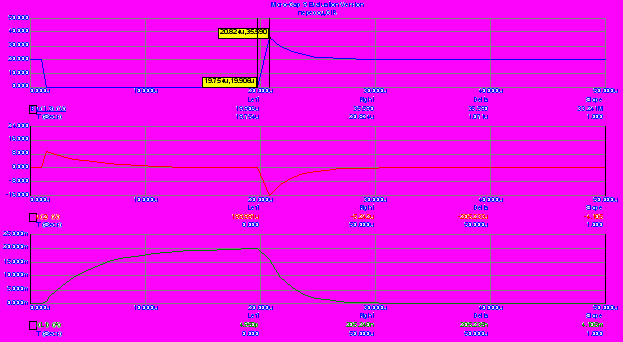
Обратите внимание, что на ключе возникает практически двойное напряжение источника, которое складывается из напряжения источника и отрицательного выброса напряжения на индуктивности. Эти перенапряжения носят название коммутационных перенапряжений и они представляют серьёзную опасность для нормальной работы электрического оборудования. Поэтому необходимо принимать меры для защиты как этих элементов, так и подходящих к ним сетей!


Схема с L , С, R и электрическим ключом.




Из всех возможных вариантов соединений этих элементов была выбрана данная цепь, так как между узлами 2 и 0 размещены аналоговые элементы, отвечающие за все 3 превращения энергии между двумя любыми точками в пространстве, занятом электромагнитным полем.

Ключ выбран нормально-открытым.

Напишем уравнение для данной цепи после первой коммутации по 1 закону Кирхгофа

при неизвестной временной зависимости тока через индуктивность и напряжения на ёмкости после коммутации. Правила коммутации можно записать для обоих неизвестных параметров.

IL = IL+ =0 UС= UС+ = 0

Учитывая, что IС= СdUC/dt и UC=ILR2+ LdIL/dt и UL= (2-0), а также заменяя источник э.д.с. Е с внутренним сопротивлением R1 на источник тока Е/R1 с таким же внутренним сопротивлением, получим

Е/R1= СdUC/dt + UC/R1+IL =CR2 dIL/dt +CLd2 IL/dt2+ ILR2/R1+ L/R1 dIL/dt + IL

Е/R1= d2 IL/dt2 + (R2/ L + 1/R1C) dIL/dt + IL(R2/R1 +1)/ LC

При R1 » R2

Е/R1= d2 IL/dt2 + (R2/ L + 1/R1C) dIL/dt + IL/LC

При R1  , то есть при наличии идеального источника тока J

J= d2 IL/dt2 + R2/ L  dIL/dt + IL/LC

При любых соотношениях R1 и R2 имеем дифференциальное уравнение второго порядка, вследствии того, что у нас в схеме 2 реактивных элемента. Если бы их было больше, мы имели бы более высокий порядок уравнения, решать которые классическим методом очень сложно из-за трудностей в решении алгебраического (характеристического) уравнения с порядком больше 3.

Правило здесь очень простое: сколько реактивных элементов, то таков же порядок дифференциального и, соответственно, характеристического уравнений.

Характеристическое уравнение для данной схемы с питанием от идеального источника тока

р2 + R2/ L  р + 1/LC=0


Отсюда р1,2=  R2/2L( R2/2L)2-1/LC

Во-первых отметим, что здесь 2 корня, то есть в результате будут 2 экспоненты – одна быстрая с р1= R2/2L+( R2/2L)2-1/CL, а другая медленная с

р2 = R2/2L(R2/2L)21/LC.

Во-вторых, дискриминант уравнения (R2/2L)2-1/CL может быть положительным или отрицательным в зависимости от соотношения R22/4L2 и 1/CL.

При R2/2L/С он будет положительным и у нас два действительных корня.

Но при R2/2L/С у нас оба корня будут содержать мнимую часть, то есть в сигнале появятся гармонические колебания с частотой 1/LC=. А это не что иное, как резонансная частота колебательного контура, образованного нашими реактивными элементами L и C. То есть, при активном сопротивлении контура R2/2 меньше чем его характеристическое сопротивление L/С, импульсное воздействие возбуждает резонансные колебания, как это было бы, если ударить по пустой бочке.

В установившемся режиме IL=J, a UC=JR2.

Решения уравнения будем искать в виде

IL=A1ep1t+A2ep2t+J

Применяя условие коммутации для тока , получим 0=A1+A2+J.

Второе условие коммутации UС= UС+ = 0 UС+ = R2 IL+ LdIL/dt

JR2 + R2 (A1+A2) + L (р1A1+р2 A2)=0

JR2 + R2 A1+ R2A2 + р1L A1+р2 L A2= JR2 + (R2 + р1L )A1+ (R2 + р2 L) A2=0

Выразим из первого условия A1= A2J и тогда

A2 = J р1/ (р2р1)

А1 = J р2/(р1р2)

Можно вернуться к начальному уравнению и произвести те же вычисления с учётом обоих сопротивлений и реальным источником. Но суть решений не изменится, увеличится только сложность коэффициентов в формулах.

Поэтому лучше посмотреть соответствующие графики.

При R1=4 кОм, R2=1кОм, C=10 нФ, L=100 мкГн , т.е. L/C « R2

В этом случае переходный процесс имеет апериодический характер, так как оба корня характеристического уравнения действительны.

Установившееся значение напряжения на ёмкости 4В и тока в индуктивности 4 мА.

Идёт спокойный экспоненциальный заряд емкости и индуктивности соответствующей энергией.





При R1=180Ом, R2=20 Ом, C=10 нФ, L=100 мкГн , т.е. L/C  R2/2

В этом случае переходный процесс имеет периодический характер с затуханием, так как оба корня характеристического уравнения имеют мнимую часть, которая отвечает ха гармонические колебания, в то время как действительная часть отвечает за затухание.

Установившееся значение напряжения на ёмкости 2В и тока в индуктивности 2 мА.

Период колебаний Т=6,5 мкс(график) 2πLC=2π10-6 (наш расчёт).





После второй коммутации ключ возвращается в разомкнутое (замкнутое) состояние и имеет очень высокое (малое) сопротивление, а энергия, накопленная в реактивных элементах, разряжается через резистор R2.


Уравнение этой цепи по 2 закону Кирхгофа

R2 IL + LdIL/dt +1/С  ILdt =0 и после дифференцирования

d2IL/dt2 + R2/LIL +1/LС IL = 0

Отсюда р2 + R2/Lр + 1/LС =0

Отсюда р1,2=  R2/2L( R2/2L)2-1/LC= R2/2LD

Это решение было рассмотрено при первой коммутации.

Установившееся значение IL= 0 и UC=0.

Решения уравнения будем искать в виде

IL=В1ep1t+В2ep2t

В момент второй коммутации  ток IL= IL+=А1еατ +А2 еβτ+J = J2, где А1 и А2, а также α и β были найдены при первой коммутации.

Применяя условие коммутации для тока, получим 0=B1+B2- J2

Второе условие коммутации

UС= UС+ = Е2 =R2 IL + L dIL/dt , где Е2 – напряжение на ёмкости в момент второй коммутации 

Е2 +R2 IL + L dIL/dt=0

Е2 +(R2 + Lр1)В1+ (R2 + Lр2)В2=0

Выразим из первого условия В1= В2+J2 и тогда

В2= Е2 + (R2+Lр1)J2 / L(р1р2)

В1= Е2 + (R2+Lp2) J2/ L(р2р1)

Воспользуемся вычислительной техникой и посмотрим решения при  больше характернного времени переходного процесса после первой коммутации, а также при 1) R1=4 кОм, R2=1кОм, C=10 нФ, L=100 мкГн , т.е. L/C « R2

В этом случае переходный процесс имеет апериодический характер, так как оба корня характеристического уравнения действительны.




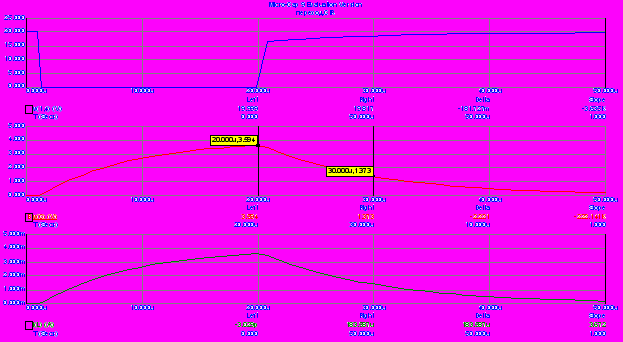
Видно, что конденсатор устраняет отрицательный выброс напряжения на индуктивности и на ключе. Такая защита катушек и ключей широко применяется в импульсной электронике, где она носит название RC-снаббера.


2) R1=180Ом, R2=20 Ом, C=10 нФ, L=100 мкГн , т.е. L/C  R2/2

В этом случае переходный процесс имеет периодический характер с затуханием, так как оба корня характеристического уравнения имеют мнимую часть




Видно, что реактивная энергия, запасённая в реактивных элементах цепи, вызывает большие затухающие колебания напряжения и тока. Отсутствие резистора R1 в цепи обмена энергией уменьшает их затухание. Это приводит к отрицательным выбросам напряжения, а также к опасному режиму работы ключа.

В цифровой электронике эти колебания могут привести к ошибкам в счёте. Если схема воспринимает как логическую единицу все напряжения выше 1,5 В (для нашего случая), то она увидит 5 логических единиц вместо одной.



Данные колебания могут распространяться как по емкостным, так и по магнитным связям. Поэтому электрические ключи являются мощным источником электромагнитных наводок, которые отрицательным образом воздействуют на соседнюю аппаратуру, и вынуждают обращать серьёзное внимание на вопросы электромагнитной совместимости работы электронных приборов.


Искажение переходными процессами идеальной единичной функции в реальных устройствах ставит задачу типизации всех возможных форм получаемых на нагрузке импульсов и визуально наблюдаемых на экране осциллографа.

Для примера возьмём полученный ранее апериодический импульс напряжения от двух переходных процессов.



Получаемый в результате действия двух коммутаций электрического ключа импульс квазипрямоугольной формы принято характеризовать длительностью, а также его фронтом и срезом. Правильные измерения этих параметров показаны на графике. Ясно, что подобная методика исключает все те мелкие переходные процессы, которые могут возникнуть в электрическом устройстве. Выделяют несколько типов импульсов, обладающих простой формой математического представления: прямоугольный, пилообразный, треугольный, трапецеидальный, экспоненциальный (рассмотренный выше), колоколообразный, полуволна, видеосигнал. Необходимо заметить, что длительность пилообразных и треугольных ипульсов измеряется по их основанию, в отличие от приведённого на графике случая.

Для описания отклонений импульса от простой математической формы могут использоваться дополнительные параметры, такие как неравномерность вершины и размер выбросов после фронта и среза.