Computer Using Educators, Inc., Usa центр новых педагогических технологий Московский областной общественный фонд новых технологий в образовании «Байтик» ано «ито» Материалы
| Вид материала | Документы |
- Computer Using Educators, Inc., Usa федерация Интернет Образования Центр новых педагогических, 2693.99kb.
- XVIII международная конференция «применение новых технологий в образовании», 160.82kb.
- XXII международная конференция «применение новых технологий в образовании», 155.52kb.
- Computer Using Educators Inc., Usa материалы, 4875.63kb.
- Computer Using Educators Inc., Usa материалы, 5788.98kb.
- Первая студенческая региональная научно-практическая конференция «Компьютерные технологии, 32.52kb.
- Положение о конкурсе областной конкурс «web-сайт года», 75.11kb.
- Положение о проведении республиканского дистанционного конкурса среди учащихся образовательных, 77.97kb.
- Опыт преподавания Web-дизайна и программирования для Internet школьникам старших классов, 34.09kb.
- «Использование новых информационных технологий в обучении английскому языку в школе», 460.19kb.
Using «Open Mathematics 2.5 Functions and Graphics» interactive course at Algebra and Basic Analysis lessons in the 10 school year
Adrova I.A. (sch 37 @ mtu-net.ru)
School 37, Moscow
Abstract
Doing «Functions and Graphics» multimedia course allows to arrange educative students' self-activity with consequent self-check, preparing additional material by using graphic illustrations, demonstrating analytic task solving, completing students' exploring activity.
Применение интерактивного курса «Открытая Математика 2.5 . Функции и Графики» на уроках алгебры и начал анализа в 10 классе
Адрова И.А. (sch 37 @ mtu-net.ru)
ГОУ средняя общеобразовательная школа № 37 города Москвы
Использование компьютерной программы «Открытая Математика 2.5. Функции и Графики» позволяет на различных этапах уроков организовать самостоятельную познавательную деятельность учащихся, оказывает неоценимую помощь в подготовке дидактического разноуровневого материала с использованием графиков-иллюстраций, помогает иллюстрировать аналитические решения заданий.
На уроке обобщения и систематизации по теме « Вычисление производных функций» эффективно применение модели 3.8 «Дифференцирование и интегрирование функций»,которая позволяет организовать индивидуальную самостоятельную работу учащегося по нахождению производных функций с последующим самоконтролем . К сожалении, не очень удачно устроена модель 3.1 «Дифференцирование функций», которая по замыслу авторов программы должна находить производную задаваемой ей функции. На самом деле при вычислении производной программа для некоторых функций выдает результаты, которые довольно трудно сопоставить с привычными результатами, например, при нахождении производной функции y=2cosx-3tgx программа выдает результат: 2·(-sinx)-(3·(1+tg2x)); ученик, решая сам, получит ответ вида: -2sinx-3/sin2x; при вычислении производной функций вида y=(ax+b)n выдается неверный ответ, например, для функции y=(3x-5)3 получается ответ: 3(3х-5)2 . При вычислении производных дробно-рациональных функций часто вообще не выдается ответа.
Эффективно также использование программы при проведении уроков в кабинете, имеющем только мультимедийный проектор. Например при изучении темы «Касательная к графику функции» можно использовать программу с целью закрепления наглядных образов касательной. Применяя модель 3.2 можно иллюстрировать решения заданий типа:
1.Составить уравнение касательной к графику функции в данной точке:
а)f(x)=2x2+1/3x3 M(-3;9); б)f(x)=
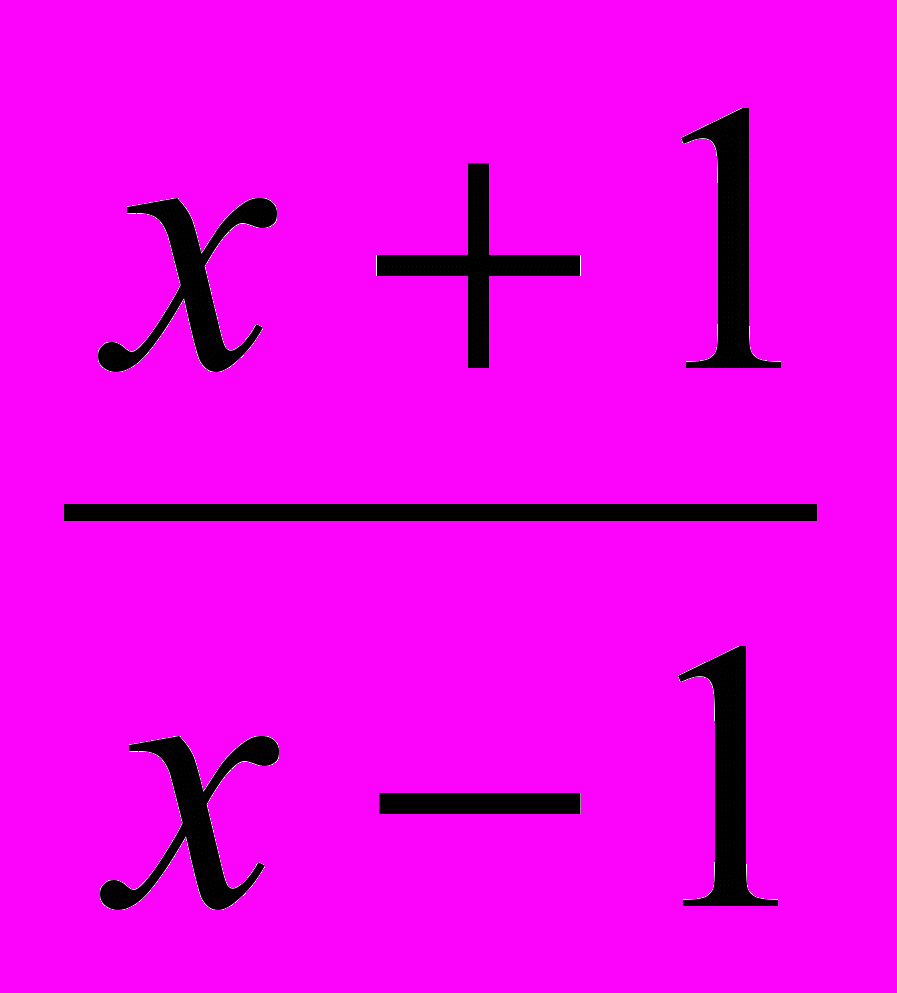; x0=2.2.На графике функции f(x) найдите точку, в которой касательная к графику f(x) к оси абсцисс под углом 45°, если f(x)=
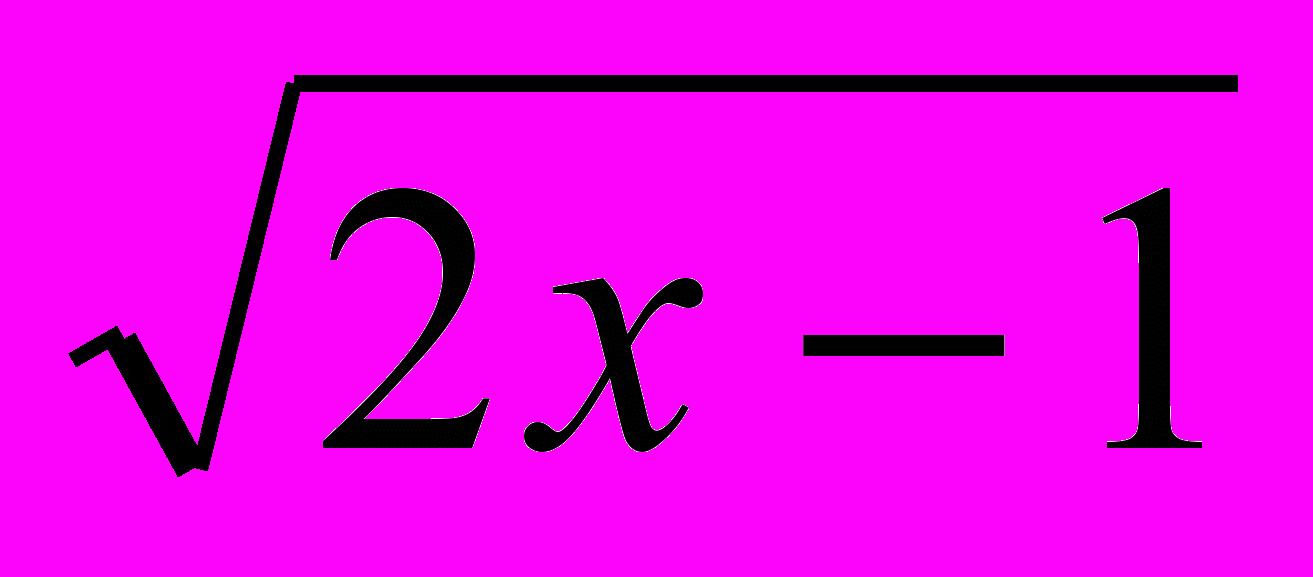.3.Прямая у=а-х является касательной к графику функции f(x)=4/x. При каких значениях а это возможно?
Для иллюстрации задания 1 используется модель 3.2 , для заданий 2;3 используется графер.
Благодаря возможностям Графера учитель может сам готовить графические иллюстрации для последующей работы с ними в классе, например, по графику функции у=f(x) с заданной касательной в точке с абсциссой х0 найти значение производной в точке х0.
Анализируя задания ЕГЭ по теме « Функции и графики» можно сделать вывод, что там при выполнении заданий учащийся должен уметь применять в одних случаях аналитический метод решения , в других умение « читать» свойства функций, заданных своими графиками. Поэтому при проведении итогового повторения по теме «Функции и графики» важно строить уроки так, чтобы они способствовали развитию навыков чтения графиков и построения графиков функций, с использованием схемы исследования функций.
Рассмотрим один из вариантов проведения такого урока в компьютерном классе. Урок построен по методу взаимоконтроля партнеров.
При подготовке к уроку учителем готовятся карточки разноуровневые по содержанию. Нечетные номера вариантов имеют в карточках первое задание на чтение графика, второе на исследование графика с помощью производной. Четные номера вариантов наоборот имеют первое задание исследование функции и построение графика с помощью производной , второе задание на чтение графика. При этом обязательно среди четных и нечетных вариантов имеются пары, в которых функции заданы одинаковыми формулами. Например: вариант№1 и вариант №2 образуют пару.
Учащиеся, имеющие первые задания на чтение графика, садятся за компьютеры и, используя графер в программе «Открытая Математика 2.5 . Функции и Графики» , строят график , заданной функции, затем отвечают на вопросы по графику в соответствии со схемой исследования функции. При этом, если они затрудняются при ответе на вопросы , могут рассмотреть задания на моделе 1.9, почитать теорию в параграфах содержания: 1.32-1.38. Выполнив первое задание полностью, ученик ищет в классе партнера-ученика у которого задана та же функция, но задание выполняется обратное: сначала исследуется функция, затем строится график. Т.к. функции у партнеров одинаковые, то свойства функций и графики должны совпадать. Обмениваясь ответами, учащиеся проверяют свою работу. Если возникают вопросы, то они обращаются к учителю. По окончании урока каждый учащийся получает оценку. Все работают в индивидуальном темпе, в режиме самоконтроля, коррекции знаний, консультирования. Применение аналитических способов решения совместно с компьютерным моделированием способствует положительному усвоению изучаемого материала, т.к. при этом работают моторная и визуальная виды памяти.
Если у учителя нет возможности проведения такого урока в компьютерном классе, то учитель готовя карточки-задания сам включает графики функций, построенные с помощью компьютера ,для чтения свойств этих функций.
Для организации проектной и исследовательской деятельности учащихся графер создает новые возможности, например, возможность построения графиков в полярных координатах и построения кривых, заданных в параметрических уравнениях. Учащимся можно предложить следующие задания:1) построить в полярных координатах график уравнения r=a+sin3j , исследовать изменения вида и свойств, полученных графиков в зависимости от а; 2) построить в полярных координатах график уравнения r=a+sin(mj/n), исследовать изменения вида и свойств полученных графиков в зависимости от а и от значений m/n; 3) построить в декартовых координатах кривые заданные параметрическим уравнениями: x=sin mt ; y=sin(mt+k). Описать свойства полученных кривых.
Программа «Открытая Математика 2.5 . Функции и Графики» дает возможность рассматривать сложный материал поэтапно, можно вернуться не только к текущему материалу, но и повторить предыдущую тему, материал, вызывающий затруднения у учеников. Использование моделей способствует повышению интереса учащихся к изучаемой теме.
Обучение носит диалоговый характер, при котором учитель в любой момент может внести необходимые коррективы. На занятиях оптимально сочетаются индивидуальная , парная и групповая формы работы. Ученики находятся в состоянии психологического комфорта при общении с компьютером.
Таким образом, использование мультимедийного курса «Функции и графики» в учебном процессе развивает познавательные способности, активность и самостоятельность учащихся, повышает интерес к овладению научными знаниями и методами научно-познавательной деятельности.
ИСПОЛЬЗОВАНИЕ НОВЫХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ КАК УСЛОВИЕ, ОБЕСПЕЧИВАЮЩЕЕ ЭФФЕКТИВНУЮ РЕАЛИЗАЦИЮ МОДЕЛИ НЕПРЕРЫВНОГО МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА
Акманова З.С. (azs@mail.ru)
Магнитогорский государственный технический университет им .Г.И .Носова
Широкое внедрение в учебный процесс вузов современных компьютерных технологий позволяет расширить арсенал методологических приемов, что повышает эффективность педагогического труда, стимулирует познавательную деятельность студентов, особенно при самостоятельной работе. Появляется возможность создания зрелищных компьютерных средств обучения с элементами графики, звука, видео, мультимедиа, гипертекста. Одним из таких средств обучения является электронный учебник — программное средство, предназначенное для представления новой информации при индивидуальном обучении, а также для тестирования знаний и умений обучаемого.
Математика в своем изложении должна обязательно сопровождаться графиками, диаграммами, вычислительными формулами и другими наглядными средствами. Поэтому математика является тем курсом, который позволяет в полной мере воспользоваться преимуществом электронного оформления.
В рамках рассматриваемой проблемы представляется актуальным для нашего вуза создание учебно-информационного комплекса по курсу математики для студентов специальности "Порошковая металлургия", который представляет собой синтез предметного учебно-методического комплекса и системы компьютерной или информационной поддержки, в состав данного комплекса входит учебное пособие на бумажных носителях и электронный учебник.
Электронный учебник позволит быстро находить необходимую информацию, обеспечивать обратную связь, проводить динамическое графическое сопровождение, моделировать результаты изменения параметров.
Рассмотрение материала каждой части учебника предлагается начать с наглядной прикладной задачи, из которой возможен аргументированный переход к традиционному изложению соответствующих разделов математики как вспомогательного инструмента решения конкретной проблемы. Таким образом, отдельные темы оказываются встроенными в общую задачу в виде разветвляющихся модулей. Изложение материала разделов сопровождается как текстом лекций, так и фрагментами демонстрационного характера, которые наглядно иллюстрируют изучаемый объект и изменения, происходящие с ним. По мере необходимости студент может возвращаться к недостаточно усвоенному разделу. Возможность многократной отработки тем ведет к закреплению полученных умений и навыков, использование встроенных модулей повышает уровень наглядности, что положительно влияет на усвоение учебного материала. Создаваемый учебно-информационный комплекс способствует более глубокому изучению математики, позволяет студентам и преподавателям освоиться в новой образовательной среде "преподаватель—студент—компьютер". При этом создаваемые электронные учебники должны быть профессионально направленными. При этом предлагаются следующие виды самостоятельной работы с использованием новых информационных технологий.
Самостоятельная работа студента с электронным учебником. Приведем пример построения электронного учебника по теме «Теория векторных полей». Данная теория в дальнейшем встречается в курсе «Физика» для расчета циркуляции напряженности электрического и магнитного полей, для вычисления энергии полей, вычисления потенциала поля при произвольном распределении заряда, в курсе «Химии» для расчета реакции в потоке. Разработка электронного учебника по векторному полю вызвана желанием помочь студентам более твердо усвоить основные понятия и применение этой теории. Основные цели данной работы:
1. познакомить студента с понятием скалярного и векторного поля и его основными характеристиками;
2. продемонстрировать эти характеристики на примерах, пояснить их физическую и химическую интерпретацию;
3. проконтролировать умение студента вычислять эти характеристики.
Предлагаемая студенту последовательность выдачи информации следующая:
Введение.
Глава 1. Скалярное поле. Характеристики скалярного поля.
1.1. Решение типовых задач.
1.2. Задачи для самостоятельного решения.
1.3. Вопросы для самоконтроля.
Глава 2. Векторные поля. Их дифференциальные характеристики.
2.1. Решение типовых задач.
2.2. Задачи для самостоятельного решения.
2.3. Вопросы для самоконтроля.
Глава 3. Задачи на нахождение интегральных характеристик векторного поля.
3.1. Решение типовых задач.
3.1. Задачи для самостоятельного решения.
3.2. Вопросы для самоконтроля.
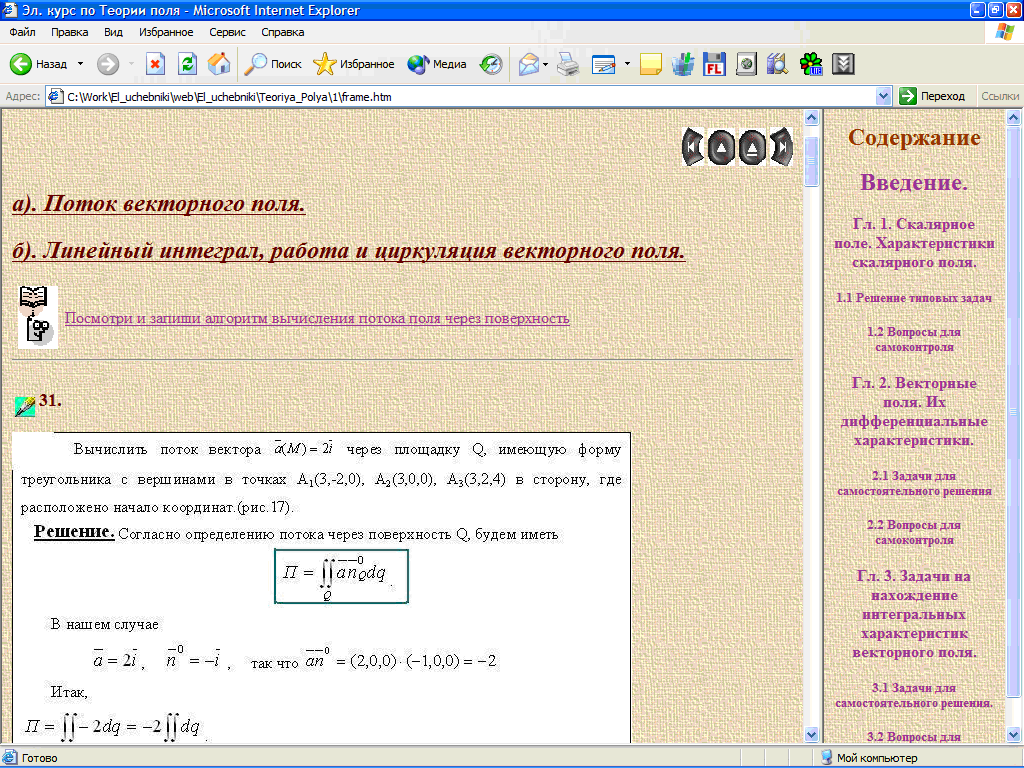
Типовые задачи должны показать студенту, как найти интегральные и дифференциальные характеристики векторных полей. Задачи для самостоятельного решения контролируют правильность усвоения материала, в случае затруднения предусмотрена клавиша «помощь», при нажатии на которую студент обращается к необходимому материалу. На рисунке приведен фрагмент электронного курса по теме «Теория поля».
Так как материал вузовской математики во многом пересекается со школьной математикой, то на довузовском и вузовском этапе нами использовались «сквозные» электронные учебники. Так, например, тема «Производная» имеет внутрипредметную и межпредметную связь. Она практически связана со всеми разделами математики, в курсе «Физики» для вычисления поверхностной и линейной плотности заряда, газовых теплоемкостей, силы тока и плотности тока, в «Химии» для вычисления энергии ионной связи и т.д. В связи с чем был создан электронный курс по теме «Техника дифференцирования», который охватывает материалы довузовского и вузовского этапов, в зависимости от уровня развития математической культуры, преподаватель может варьировать, определять объем изучаемого материала.
Использование ЭВМ при изучении курса высшей математики возможно также при проведении текущего контроля. Так, например, на кафедре нашего вуза была написана программа для проведения контрольной работы по теме: «Непосредственное интегрирование». Опыт показывает, что при этом уменьшаются затраты на проверку этих контрольных работ. Программа составлена таким образом, что выводится результат прохождения программы студентом и оценка этого результата в виде числа правильных ответов, общего числа заданий и времени, затраченного на тестирование. Контроль ведется на основе многовариантного ответа.
Составление электронного учебника студентами. Такой вид работы предусматривает переработку материала, выделение понятий, свойств, теорем, выстраивание структурно - логической цепочки, подбор заданий, выявление внутрипредметных и межпредметных связей данного материала, а также предоставление материала, его оформление, а главное стиль изложения. Данный вид работы мы предлагали студентам 1 курса 2 семестра, которая выполняется под руководством преподавателя.
Лабораторные работы с использованием ЭВМ. Формированию познавательной самостоятельности студентов способствует выполнение ими лабораторных работ по высшей математике с помощью ЭВМ. При этом студент обращается к ЭВМ с целью выполнении громоздких расчётов, а также для того чтобы уточнить значения некоторых необходимых постоянных величин (параметров). Такие работы выполняются на вузовском этапе. Так в курсе математики для студентов – технологов предусмотрено выполнение 9 лабораторных работ. В таблице представлены названия лабораторных работ и соответствующие для этого ППС.
1. Метод хорд и касательных решения алгебраических уравнений. ExcelMathcad
2. Приближенное вычисление определенного интеграла по формулам трапеции и Симпсона. ExcelMathcadMaple
3. Приближенное решение СЛАУ методом итерации и методом Гаусса с выбором главного элемента. ExcelMathcadMaple
4. Метод наименьших квадратов определения вида функциональной зависимости по данным эксперимента. ExcelMathcadMaple
5. Численные методы решения дифференциальных уравнений. ExcelMathcadMaple
6. Первичная обработка статистических данных. ExcelStatistica
7. Статистическая оценка параметров распределения. ExcelStatistica
8. Статистическая проверка гипотезы о нормальности распределения генеральной совокупности по критерию согласия Пирсона. ExcelStatistica
9. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным. ExcelStatistica
Организация такой работы требует от преподавателя огромной математической подготовки, знание как старых, так и новых ветвей математической науки, современных математических методов и информационных технологий, их использование в современном производстве.
Features of teaching of a rate of
“Concept of modern natural sciences"
Aksenova E. (Kurapova@educom.ru, LKurapova@yandex.ru)
IAC Department of education, Moscow
Abstract
In the report features of teaching of a rate of “Concept of modern natural sciences" (KSE) in pedagogical high school are considered. The expediency of use IKT is proved at creation of new techniques of training KSE. Experience of designing of the educational environment of rate KSE is considered on the basis of dynamic slides-lectures.
Проектирование образовательной среды курса «Концепции современного естествознания» на основе динамических слайд-лекций
Аксенова Е.И. (Kurapova@educom.ru, LKurapova@yandex.ru)
Информационно-аналитический центр Департамента образования города Москвы
Курс «Концепции современного естествознания» (КСЕ) введен в систему высшего профессионального образования сравнительно недавно, в середине 90-х годов XX в. и является обязательным как для естественнонаучных, так и для гуманитарных специальностей. Преподавание курса КСЕ в вузах имеет стратегически важное значение для модернизации профессионального образования, так как позволяет реализовать новую парадигму высшего образования – фундаментальность и целостность образования.
В процессе реформирования образования значительно изменяется роль высшего профессионального образования, в частности педагогического. Наиболее актуальной становится задача формирования целостности системы передачи знаний от поколения к поколению в условиях постоянного увеличения объемов информации. И поэтому учитель должен обладать помимо фундаментальных знаний по изучаемой специальности, знаниями в области возрастной психологии, дидактики, методики, и, конечно, иметь целостное представление о современной картине мира. Такие общесистемные знания об эволюции развития природы и человека можно получить в наиболее полном объеме при изучении курса КСЕ.
Результатом исследования существующих современных образовательных технологий, основных методик преподавания в вузе, стало решение о необходимости проектирования образовательной среды курса КСЕ.
Компонентами образовательной среды курса КСЕ являются:
1. Комплект динамических слайд-лекций по курсу КСЕ.
2. Лекционный модуль по курсу КСЕ.
3. Комплект компьютерных демонстраций по курсу КСЕ.
4. Модуль контроля знаний по курсу КСЕ.
5. Методическое пособие для преподавателя по курсу КСЕ.
6. Программная оболочка и модуль администрирования.
Образовательная среда курса КСЕ в понимании автора статьи – это интеграция традиционного информационно-иллюстративного обучения и мультимедиа-технологий обучения.
Динамическая слайд-лекция – это законченный тематический модуль, имеющий сложную систему взаимосвязей с возможностью выхода в меню с любого слайда. Существует возможность перемещения по учебной информации не только на горизонтальном уровне, то есть от слайда к слайду и обратно, но и переходить при необходимости на вертикальный уровень, то есть перемещаться по темам. Это достигается с помощью организации учебного материала с использованием гиперссылок. Это позволяет устанавливать эксплицитные, явные связи между иерархически организованными фрагментами.
Предлагаемая технология слайд-лекции не устраняет лектора из учебного процесса. Основной звуковой ряд лекции – это голос самого лектора, который диктует формулировки законов, определений, комментирует содержимое слайдов, регулирует темп лекции и смены слайдов. Но при такой организации учебного процесса изменяется не только роль преподавателя, но и студента. Студент постоянно включен в него через образовательную среду курса КСЕ. Занятия в форме слайд-лекции переходят из плоскости усвоения в плоскость исследования, максимально реализуются функции лекции. При этом вырастает эмоциональный фактор в восприятии студентами нового материала, повышается уровень лекций и в полном объеме остается общение студентов с преподавателем.
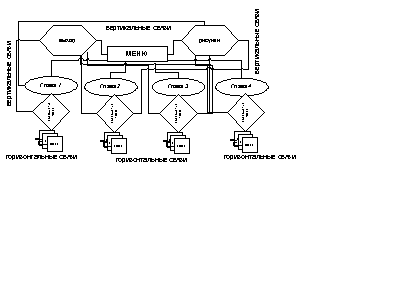
Архитектуру динамической слайд-лекции по тематическому модулю можно представить в следующем виде:
В рамках апробации созданной образовательной среды курса КСЕ в Московском государственном педагогическом университете (МПГУ) на математическом факультете, был разработан модуль «Космология» курса КСЕ. Этот модуль включает в себя изучение вопросов современной космологии, моделей вселенной, темной материи, скрытой массы, эволюции звезд, черных дыры и сверхновых.
Особенностями модуля «Космология» являются:
1. Блочно-модульная структура модуля «Космология» курса КСЕ.
2. Формализация учебного материала. Формулы. Законы.
3. Визуализация учебного материала. Фото космических объектов, Фото ученых.
4. Анимация космических эффектов. Моделирование астрономических и космических экспериментов.
И в заключении, стоит отметить, что, представленная выше методика изложения учебного материала в виде динамической слайд-лекции, сближает очное и дистанционное обучение и позволяет интегрировать в кратчайшие сроки стандартные формы очного обучения в дистанционные с помощью Интернет-технологий, которые в процессе эволюции системы образования может занять значительное место.Литература
- Сивергин М.Ю. В сб.: Труды СГУ/Специальный выпуск 41 «Гуманитарные науки». М.: СГУ, 2002. С. 150.
- Васильев В.Н., Парфенов В.Г., Столяр С.Е. В сб.: Современные образовательные технологии/Сб. статей. СПб: СПб ГИТМО (ТУ), 2001. С. 46.
- Сажин М. В. Современная космология в популярном изложении. М.:Едиториал УРСС, 2002. – 240с.
- Хокинг Стивен Краткая история времени от большого взрыва до черных дыр. М.:Амфора, 2003. – 268с.