1 Проблема познаваемости мира в истории философии

Вид материала

Документы

Содержание В и связанный с ним гиперзаряд Y. 4пр тогда как для одномерного случая решение будет иметь вид ip = r/2v, (г X. Следовательно, координата электрона будет измерена с неопределенностью Дх~А.. Для того, чтобы уменьшить Ах, нужно уменьшить X

Подобный материал:

• «Проблема взаимоотношения человека и мира в социальной онтологии», 368.23kb.
• Темы рефератов диалектическая, метафизическая и креационистская модели развития мира, 52.45kb.
• Проблема жизни, смерти, бессмертия мира, человечества, человека в контексте истории, 302.24kb.
• Нп «сибирская ассоциация консультантов», 206.84kb.
• Вопросы к зачету по курсу «история философии в украине», 20.13kb.
• Проблема реализма и основные концепции соотношения языка и реальности в аналитической, 579.92kb.
• Учебно-методический комплекс специального курса «Проблема человека в Древнегреческой, 209.13kb.
• Учебно-методический комплекс специального курса «Проблема человека в Древнегреческой, 256.77kb.
• Программа минимум кандидатского экзамена по специальности 09. 00. 03 «Истории философии», 494.66kb.
• Проблема следования правилу как проявление радикального эпистемологического скептицизма, 547.43kb.

по


размерности. Но этот случай не очень интересен и мы рассмотрим самый распространенный вариант — введение в уравнение дополни­тельных членов. Именно к этому типу относится уже обсуждавшаяся гипотеза тока смещения Максвелла. Как вы помните, она состояла в том, что в одно из уравнений был просто дописан дополнительный

ldE

член ——. с dt

Интерес подобного рода гипотез состоит в том, что интерпретация таких дополнительных членовдалеко не всегда ясна в момент введе­ния гипотезы. В таких случаях решение проблемы интерпретации откладывается на более позднее время. Мы всегда надеемся, что такая интерпретация (физический смысл) будет найдена.

В связи с этим я хочу рассмотреть исключительно интересный случай математической гипотезы — получение Планком знаменитой формулы распределения плотности энергии излучения абсолютно черного тела по частотам

87rf² hv

^Ы" с^ъ exp[hv/kT\-\

В большинстве книг по истории физики (я думаю, что и вам так го­ворили) утверждается, что М. Планк получил эту формулу, сделав ин­терполяцию между формулами Рэлея-Джинса и Вина. И сам М. Планк говорил так в 1908 году. Однако в книгеГанса Георга Шепфа «От Кирх­гофа до Планка» (М., 1981) абсолютно аргументированно показано, что это совершенно неверно. Путь М. Планка был совсем иным.

Начатые в конце 80-х годов исследования распределения плотно­сти энергии излучения черного тела обнаружили, что это распреде­ление очень напоминает максвелловское. Это позволило Вильгельму Карлу Вину (1864-1928) в 1896 году предложить полуэмпирическую формулу:

В. Вин давал своей формуле довольно странное обоснование. Он предположил, что молекулы газа, которые движутся в полости и име­ют максвелловское распределение, излучают с частотой и интенсив­ностью, зависящей от скорости.

М. Планк был неудовлетворен таким обоснованием и поставил перед собой задачу получить формулу Вина, не прибегая к модельным гипотезам, а используя только термодинамический подход. Обра­тим внимание на то, что в постановке задачи Планком чувствуется сильное влияние индуктивистского стиля мышления: модельные гипотезы представлялись ему недостаточно строгими, тогда как тер­модинамика, основанная на индуктивно обоснованных принципах, рассматривалась как эталон строгости.


111

М. Планку не удалось полностью реализовать программу «безмо­дельного» чисто термодинамического вывода формулы Вина. Но вме­сто модели молекулы, излучающей с частотой v - У², он использует модель дипольного излучателя Герца с затуханием, находящегося в электромагнитном поле излучения, отдельного монохроатического линейно поляризованного пучка.

При этом М. Планк исходит из идеи необратимости процесса из­лучения осциллятора, связывает эту необратимость со вторым зако­ном термодинамики и вводит температуру и энтропию одного осцил­лятора и пучка излучения. По сути дела, он рассматривает средние значения коллектива осцилляторов, подчиняющихся статистике Больцмана.

Таким образом, М. Планк получает два уравнения:

ds ₌ 1

dU~ T'

d²s _ a

~dU^J~~U'

Первое уравнение есть чисто термодинамическое (опрделение эн­тропии, или иначе — температуры), а второе — следствие статисти­ческой модели.

Интегрируя эти уравнения, М. Планк получил формулу излучения Вина. Это произошло в начале 1900 года, и в том же самом году не­мецкие экспериментаторы надежно установили отклонения от закона Вина в области больших длин волн (малых частот). Для того чтобы разрешить это противоречие, М. Планк идет по пути модификации уравнения для энтропии

d²s a

Интегрируя это уравнение (совместно с ds/dU=l/T), Планк по­лучает свое знаменитое распределение, очень точно описываю­щее распределение плотности энергии излучения черного тела. То есть Планк использовал типичную математическую гипоте­зу — вписал в уравнение для энтропии дополнительный (квадратич­ный) член.

Сам М. Планк не был вполне удовлетворен таким выводом. Он считал, что такая модификация несет в себе слишком большую про­извольность, и после 1906 г. предпочитал говорить об интерполяции формул Вина и Рэлея-Джинса. Такая интерполяция представлялась ему более «индуктивистской». Для нас в конце XX века прием План­ка отнюдь не выглядит столь странным — ну, подумаешь, большое дело — ввели первую нелинейную поправку. Мы уже привыкли к это­му. Но во времена Планка, я напоминаю, влияние индуктивистской идеологии было еще очень велико.











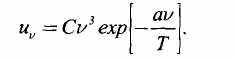
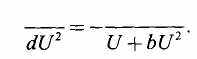
112


113

Обратимся, однако, к более интересному аспекту гипотезы План­ка. Я уже говорил, что нередкой является ситуация, когда интер­претация нового введенного в уравнение члена отсутствует, и тогда возникает проблема. Именно так обстоит дело в гипотезе Планка. Каков физический смысл дополнительного члена? И М. Планк обна­ружил, что если вычислять больцмановскую статистическую сумму осциллятора, то нужно перейти от интегрирования по непрерывному множеству возможных энергий осциллятора к дискретному сумми­рованию по энергиям E=nhv. Так в физику вошло квантование энер­гии осциллятора, что стало началом квантовой теории. Вы видите, к какому грандиозному результату привела сравнительно простая модификация уравнения!

Этот пример превосходно иллюстрирует два аспекта познаватель­ной деятельности:

- очень высокую эффективность метода математических ги­потез;

- принципиальную важность решения проблемы интерпретаиии. о которой мы говорили, когда характеризовали структуру на­учной теории.

Последним типом гипотез, который я намерен рассмотреть, явля­ются сложные гипотезы, какими являются концепции. О концепциях как гипотетических конструкциях мы уже говорили, когда противо­поставляли теорию и концепцию. Теперь я намерен несколько больше сказать о структуре концепции.

Обычно гипотезы выражаются в форме одного предположения, которое имеет довольно четкий характер. Возможные изменения в рамках этого предположения невелики. В отличие от этих типов, концепции включают в себя, как правило, несколько предположе­ний, и эти предположения носят более «свободный» характер, то есть допускают довольно значительные вариации. Эта вариативность обеспечивает концепциям довольно большую гибкость, возмож­ность приспосабливать их к изменениям в эмпирическом материале. Очень часто (может быть, даже почти всегда) концепции включают в себя широкие обобщения, основанные на эмпирических данных. В этом аспекте концепции более «индуктивны», нежели другие виды гипотез.

Классическим примером концепции является эволюционная кон­цепция Ч. Дарвина (или в современном варианте — синтетическая «теория» эволюции). Концепция Дарвина основана на очень боль­шом эмпирическом материале сравнения форм биологических видов. Индуктивным обобщением является утверждение о близости форм биологических видов и о наличии рядов близостей. Далее следует гипотеза, решающая проблему этих близостей — гипотеза о том, что эта близость является следствием биологической эволюции — проис­хождения одних видов от других. Следующее предположение — это


предположение о механизме закрепления (или не закрепления) изме­нений — гипотеза естественного отбора. Что же касается механизма возникновения самих изменений, то здесь Ч. Дарвин сам испытывал колебания между идеей резкого мутационного изменения и ламарки­стской идеей медленных плавных изменений.

То обстоятельство, что концепции содержат обычно несколько предположений, придает им характер достаточно развитых сис­тем. Но это же и делает концепции уязвимыми с гносеологиче­ской точки зрения — каждое предположение, входящее в концеп­цию, требует отдельного анализа и обоснования. Это обстоятель­ство чаще всего является поводом для сомнения в состоятельности концепции.

И здесь мы снова обращаемся к вопросу об обосновании гипотез. Основным моментом в обосновании гипотезы является указание на то, какую познавательную проблему решает введение данной ги­потезы. Но введение предположения само создает познавательную проблему. И тут появляется искушение решить эту новую пробле­му путем введения новой гипотезы. И таким образом может быть выстроена целая пирамида, нагромождение гипотез. Очень многие концепции как раз носят характер таких пирамид. Особенно это характерно для концепций общества. В естествознании концепции обычно выстраиваются достаточно осторожно, они включают два-три независимых предположения, но в концепциях общества число таких предположений может доходить до семи-восьми. В этом отношении особенно показательна концепция Льва Николаевича Гумилева (1912— 1992). Число независимых предположений в ней с трудом поддается учету.

В целом можно сказать, что наука «не любит» конструкций, вклю­чающих одновременно большое число независимых предположений. Полностью отказаться от сложных концепций в научном познании невозможно, но нужно стремиться не к наращиванию гипотез, а к ог­раничению их числа. Но самое главное состоит в абсолютной необхо­димости выполнить фундаментальные требования научного метода:

- Нельзя выдавать гипотезу (предположение) за знание.

- Нельзя гипотезу считать основанием для введения новой ги­потезы. Новую гипотезу надо рассматривать именно как не зависимое предположение.

Оба эти требования являются категорическими, и их нарушения немедленно выводят за рамки научности.

Вернемся к вопросу об обосновании гипотез. Собственно говоря, обоснование гипотезы не может быть отделено от способа, метода ее выдвижения. То есть речь все время идет о научном методе. Когда речь идет о математических гипотезах, то в качестве обоснования выбора (подчеркиваю — не доказательства, а именно обоснования),

114


часто используются соображения, основанные на простоте и симмет­рии. Однако больший интерес представляют гипотезы, основанные на индуктивных обобщениях. Их интересность связана с тем, что такие обобщения обычно связаны с более широким аспектом, углом зрения. В них весьма отчетливо выступает синтетическая функция теоретического уровня.

Наиболее прозрачным является индуктивное обобщение самих опытных фактов. При этом, конечно, не надо забывать о многоуров­невой иерархической структуре самих фактов. Обобщение может быть сделано и на уровне первичных фактов, и на уровне фактов высокого порядка. Приведем в качестве очень хорошего примера индуктивное обобщение, сделанное на весьма высоком уровне.

Еще в конце 30-х годов нашего века В. Гейзенберг, осмысливая одинаковость сильного (ядерного) взаимодействия протонов и ней­тронов, ввел предположение о том, что протон и нейтрон являются разными состояниями одной частицы (потому и взаимодействие у них одинаковое). Эта частица обладает характеристикой, которая была названа «изотопическим спином» и которая, по аналогии с обычным спином, может иметь только два значения «проекции в изотопиче­ском пространстве» Т_г. Одной проекции соответствует состояние ней­трона, а другой — протона.

В дальнейшем эта гипотеза оказалась очень плодотворной для классификации сильно взаимодействующих частиц. И понятие изо-спина Т и его «проекции» Т_г стало важным элементом теории.

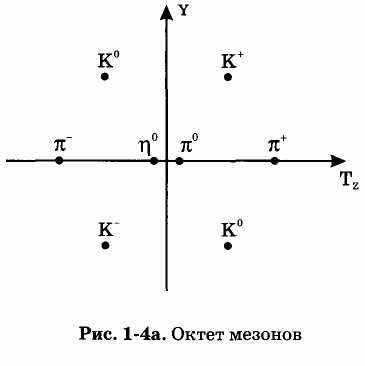
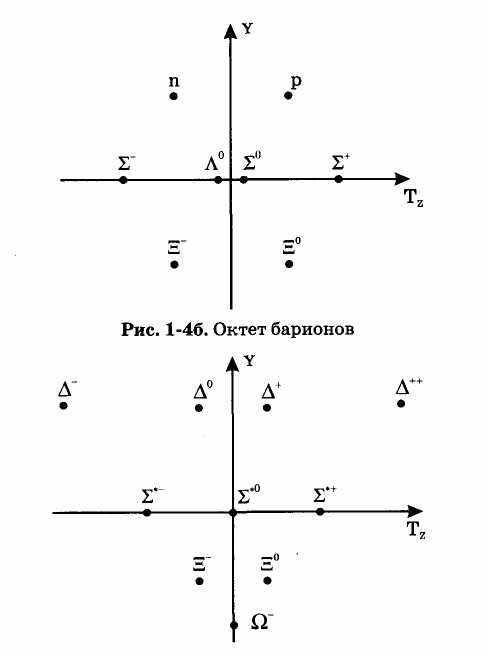
В послевоенное время была введена еще одна характеристика — барионное число В и связанный с ним гиперзаряд Y.

Изучение сильно взаимодействующих частиц показало, что в ко­ординатах У-Т_г они группируются в семейства — октеты, декупле-ты. Причем в координатах Y-T_z эти семейства имеют очень интерес­ный вид:


115

Рис. 1-5. Декуплет барионов

Так вот, в одном из семейств типа декуплета не хватало вершины треугольника.

Естественным индуктивным обобщением опытных данных яви­лась гипотеза о том, что пустующей вершине соответствует еще неот­крытая частица. Очень быстро эта частица была открыта и известна как 2~-гиперон. Этот тип гипотез — индуктивных обобщений доволь­но прозрачен.

Более сложный характер носят гипотезы, основанные на анало­гиях. Они интересны тем, что в них часто соединяются индуктивные обобщения с элементами математической гипотезы.

Вообще говоря, использование аналогий очень широко распростра­нено в научном познании, и метод аналогий заслуживает самостоя­тельного изучения. Мы уже встречались с методом аналогий, когда рассматривали модельные аналоговые эксперименты. Но в данном разделе курса нас интересует использование аналогий на теорети­ческом уровне научного познания. На этом уровне использование





116


аналогии состоит в перенесении закономерностей с уже изученного класса (или области) явлений на еще неизученный. Этот прием об­ладает огромной мощью, и в целом все развитие науки связано с его использованием.

Одним из первых применений метода аналогий была гипотеза Гюйгенса о волновой природе света. Она основывалась на аналогии между интерференцией волн на поверхности воды и наблюдаемыми световыми явлениями. Хочу отметить, что волновая гипотеза Гюйген­са была выдвинута раньше, чем корпускулярная гипотеза Ньютона. Однако понадобилось больше ста лет, чтобы эта гипотеза была раз­работана до волновой теории. Я думаю, что все вы помните об опти­ко-механической аналогии Гамильтона. В дальнейшем эта аналогия сыграла огромную роль в развитии физики. Именно руководствуясь этой аналогией, Эрвин Шредингер получил свое знаменитое уравне­ние. Метод аналогий был очень активно использован Дж. Максвеллом при создании им системы уравнений электродинамики.

С еще одним очень интересным проявлением аналогии мы встре­тимся, когда будем изучать принцип соответствия в разделе курса, посвященном методологическим принципам научного познания. Я имею в виду то обстоятельство, что уравнения квантовой механи­ки можно получать по аналогии, заменяя в классических уравнениях физические величины операторами. И, наконец, переход к квантовой теории поля в начале 30-х годов нашего века был тоже сделан по ана­логии — поле было разложено на фурье-компоненты — элементарные осцилляторы, а к этим полевым осцилляторам применены правила квантования «обычного» осциллятора.

На этих примерах вы сами можете оценить значение метода ана­логий в развитии науки.

Использование аналогий на теоретическом уровне представляет собой очень интересное проявление индукции. Обычно индукцию рассматривают на уровне обобщения единичных фактов. Но исполь­зование аналогий представляет собой и обобщение на уровне законо­мерностей. Этот аспект индуктивного подхода изучен недостаточно хорошо. Но я хочу напомнить, что еще в 1620 году Ф. Бэкон рассмат­ривал индукцию как сложный многоступенчатый процесс. Нижнюю ступень образуют обобщения единичных фактов. На более высоком уровне обобщению подвергаются уже не единичные факты, а обобще­ния низшего уровня, и происходит переход к обобщениям среднего уровня. И далее, обобщения среднего уровня еще раз обобщаются в высший уровень. Вообще говоря, можно выделить не три, а большее число уровней, но этот вопрос нас сейчас не интересует.

Использование аналогий на теоретическом уровне научного позна­ния представляет собой индукцию высших ступеней. И здесь опять мы видим глубокое единство методов индукции и гипотезы. Индук­ция, в особенности в форме аналогии, представляет собой способ фор­мирования гипотезы.


117

Используя аналогию как способ формирования гипотез, необходи­мо соблюдать общие требования научного метода. Первое и главное из них состоит в том, что аналогия не может быть доказательством правильности гипотезы. Аналогия является основанием для выдви­жения гипотезы, но проверяться гипотеза должна независимо от той аналогии, на базе которой она была выдвинута. Второе требование достаточно тесно связано с первым, хотя и не совпадает с ним полно­стью. Его содержание связано с'тем, что почти все (может быть, даже просто — все, но я буду осторожен и не категоричен — почти все) аналогии не являются полными. Мы это уже видели на примере ма­териальных и субстратноподобных, и субстратнонеподобных анало­гий. Все они имеют какие-то границы применимости. В еще большей степени это относится к теоретическим аналогиям. Именно по этой причине аналогия может быть только основой для гипотезы.

Оба отмеченных аспекта известны достаточно давно. Афоризм «аналогия — не доказательство» очень старый. А о неполноте анало­гий знал еще Аристотель. В рамках своего двузначного логического подхода он квалифицировал любой вывод по аналогии как ошибоч­ный. Но я хочу еще раз отметить, что научный подход и научное мыш­ление не являются формально-логическими. Так, Аристотелю (судя по его текстам) было просто неизвестно понятие приближенности знания, а также понятие гипотезы как предположения, подлежащего проверке. Но мы рассуждение «по аналогии» квалифицируем как логичное, но не как доказательство.

Я хочу обратить ваше внимание на то, как тесно переплетаются метод индукции, метод гипотез и метод аналогий. Это обстоятельство вовсе не случайно. И мы еще будем говорить об этом подробнее. На­учный метод обладает очень мощным внутренним единством. Это не просто совокупность эффективных приемов, это — научный метод, то, что, собственно, и создает науку. Но к этому вопросу мы обратимся при обсуждении методологических принципов научного познания.

А теперь я перейду к обсуждению четырех методов научного по­знания, замыкающих весь этот раздел курса — аксиоматического метода, метода моделирования, метода «мысленного эксперимента» и метода «математического эксперимента».

3.3.3. Аксиоматический метод в научном познании

Аксиоматический метод является исключительно методом тео­ретического уровня, в нем нет ничего, что носило бы эмпирический оттенок. Смысл аксиоматического метода состоит в выделении фун­даментальных положений теории в качестве основных независимых аксиом и дедуктивном построении всей остальной структуры теории (кроме математического аппарата) на основе этой системы аксиом. Я думаю, что для вас очевидна связь аксиоматического метода с гипо-тетико-дедуктивистским подходом. И дефектность всей этой идеоло­гии, ее ограниченность выражается в ограниченности возможностей

118


аксиоматического метода. Собственно говоря, в современной физике нет ни одной полностью аксиоматизированной теории. Наиболее пол­ные попытки аксиоматизированного построения предпринимались в термодинамике. Известны аксиоматики термодинамики Татьяны Алексеевны Афанасьевой-Эренфест (1876-1964) и Каратеодори.

Следующая крупная попытка аксиоматизированного построения теории была предпринята в 1960-е годы группой физиков-теорети­ков с явным математическим уклоном (А. С. Вайтман, Р. Ф. Стритер, Н. Н. Боголюбов), которые попытались создать строго аксиомати­зированную квантовую теорию поля. На этом пути они надеялись решить ряд трудностей, присущих неаксиоматизированной «фи­зической» квантовой теории поля. В 1960-1970-е годы было пред­принято несколько попыток построить аксиоматическую квантовую теорию поля. Известны аксиоматики Вайтмана, Лемана-Симан-цика-Циммермана, Хаага, Боголюбова. Эти аксиоматики иногда значительно отличаются друг от друга. Основное отличие состоит в отношении к таким динамическим переменным, как квантован­ные поля, выраженные при помощи операторов рождения и погло­щения. Одни аксиоматики включают в число аксиом определения квантованных полей, другие стремятся к отказу от их использования и замене их S-матрицей (матрицей рассеяния), матричными элемен­тами которой являются амплитуды перехода из одного состояния в другое.

Существование разных систем аксиом затрудняет подробное рас­смотрение, поэтому я постараюсь в качестве примера выделить наи­более общие положения разных аксиоматик.

В качестве одного из основных во всех аксиоматиках фигурирует требование релятивистской инвариантности или, в более широком смысле, инвариантности относительно группы Пуанкаре. Я думаю, это всем понятно и каких-либо комментариев не требует.

Вторая аксиома, которую я хочу выделить как общую, это аксиома спектральности или эквивалентные ей требования. В аксиоматике, использующей локальные квантованные поля, требование спектраль­ности состоит в том, что оператор 4-импульса должен иметь в качестве собственных функций полную систему и спектр оператора энергии неотрицателен, т. е. квантованное поле не должно «проваливаться» в «минус бесконечность» по энергии. Последнее требование по сути дела означает стабильность вакуума. В аксиоматиках, основанных на использовании S-матрицы, также существуют требования полноты системы состояний и инвариантности вакуума относительно S-мат­рицы, эквивалентные аксиоме спектральности.

Третья общая аксиома — аксиома унитарности. Она особенно су­щественна в аксиоматике S-матрицы и состоит в требовании унитар­ности S-матрицы (SS⁺=1). Смысл этой аксиомы состоит в том, что сумма вероятностей всех возможных переходов должна быть равна 1. Ее аналогом является требование нормируемости вектора состояния.

И, наконец, совершенно общей является аксиома причинности. Смысл аксиомы причинности состоит в необходимости выполне­ния требования, что следствие не может предшествовать причине, или, с учетом релятивистской инвариантности, причину и следствие должен разделять времениподобный интервал. Вообще, требование причинности мы будем обсуждать позже в разделе, посвященном анализу методологических принципов научного познания. Здесь я хочу отметить, что условие причинности может быть по-разному сформулировано для квантованных полей. Оно может быть записано как условие некоммутативности полевых переменных в точках, раз­деленных пространственноподобным интервалом, или как условие, связывающее асимптотические квантованные поля — входящие и вы­ходящие. Но так или иначе, все эти условия эквивалентны некоторым требованиям аналитичности матричных элементов S-матрицы.

Использование аксиоматического подхода дало возможность до­казать некоторые общие теоремы, представляющие интерес для бо­лее глубокого понимания структуры физической квантовой теории поля. Однако в рамках аксиоматического подхода не удалось решить принципиальных проблем, а тем более добиться какого-либо продви­жения вперед в физике. Эти продвижения — создание единой теории электромагнитных и слабых (электрослабых) взаимодействий и тео­рии сильных взаимодействий — квантовой хромодинамики, были сделаны именно в физической (неаксиоматизированной) теории. Это говорит о том, что возможности метода аксиоматизации довольно ог­раничены. Он действительно пригоден не столько для продвижения в создании новых теорий, сколько для упорядочивания структуры уже построенных. И с этим связана ограниченность его распростра­ненности в научном познании.

3.3.4. Метод моделирования

Метод моделирования в научном познании применяется исклю­чительно широко и имеет очень общий характер. Он не является специфическим методом теоретического уровня, подобно методу ак­сиоматизации, и применяется как на эмпирическом, так и на теоре­тическом уровнях.

Использование метода моделирования на эмпирическом уровне мы уже обсуждали, когда рассматривали модельные эксперименты. Но на теоретическом уровне метод моделирования обладает очень сильной специфичностью, которую нам и предстоит обсудить.

Напомню, что в общем смысле метод моделирования состоит в том, что мы заменяем исследуемый объект его представителем — моделью. Т. е. модель определена по отношению к чему-то, по отношению к не­которому «оригиналу». Когда речь идет о материальных моделях, как это было в модельном эксперименте, то тут все понятно. Но когда речь идет об идеальных моделях, то дело становится существенно сложнее. Любая теория есть идеальная модель некоторого круга яв-

122


ближенного метода. Это обстоятельство связывает метод моделирова­ния с тестовыми задачами в методе математического эксперимента. И с этим же аспектом связано частое использование моделей — «иг­рушечных теорий» — в процессе обучения. Студентов очень удобно учить на примерах таких моделей.

Приведем несколько примеров подобного рода моделей.

В исследованиях по квантовой теории поля очень часто использу­ются двумерные модели. То есть рассматривается квантованное поле в пространстве-времени с одной пространственной и одной временной переменной. Очевидно, что мир, в котором мы живем, не 2-мерный, а как минимум 4-мерный, и что 2-мерная модель есть именно модель. Но для выявления многих интересных свойств квантовой теории поля двумерные модели оказались очень полезны. Широко известны дву­мерные сигма-модель и модель Тирринга. При этом важно, что дву­мерные модели очень часто допускают точные решения.

Кстати, аналогичный прием очень часто использовалсяне только в квантовой теории поля, но и в физике вообще. Только в нереляти­вистской физике такие модели назывались одноерными. При этом я хочу отметить различие между одномерными моделями и реаль­ными ситуациями, когда в силу симметрии задача сводится к одно­мерной.

Но здесь надо обязательно помнить, что модель с измененным числом размерностей в некоторых случаях может оказаться очень неадекватной. Например, если мы будем рассматривать уравнения Пуассона с точечным источником:

то в трехмерном случае для потенциала мы получаем закон Ньюто­на-Кулона j

¥ ,

4пр

тогда как для одномерного случая решение будет иметь вид

ip = r/2v, (г = 1x1).

В трехмерном случае в кулоновском потенциале могут сущест­вовать как финитные, так и инфинитные движения (связанные со­стояния и свободные), тогда как в одномерном существуют только финитные движения (связанные состояния).

И все же, несмотря на возможность столь существенных качест­венных различий, модели с меньшим числом размерностей исполь­зуются очень часто.

Другим примером использования метода моделирования в физике микромира являются модели мира с ограниченным числом типов частиц. Хорошо известно, что число типов элементарных частиц в на­шем мире превышает две сотни, и даже если рассматривать только известные в настоящее время фундаментальные частицы — кварки, лептоны и бозоны, переносящие взаимодействия, то число известных астиц составляет 24 фндаментальных фермиона (и стольк же анти-


123

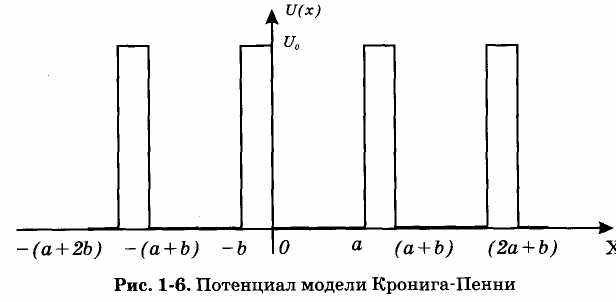
Эта модель имеет точное решение, которое, однако, представлят-ся довольно сложным трансцедентным выражением. Поэтому для получения решения делают еще одно упрощение: и так, что величина остается постоянной. В этом предположении задачу легко решить графически. Модель Кронига-Пенни передает такие черты реаль­ных твердых тел, как периодический характер волновой функции электрона (блоховские волновые функции) и наличие разрешенных и запрещенных зон в спектре энергии.

Моделей такого рода в физике очень много, и я думаю, что каждый из вас может привести подобные примеры из своей учебной практики и из своей конкретной области науки.











124


Но, кроме таких моделей, предназначенных для чисто качествен­ного понимания, в науке бывают и другие модели, целью которых яв­ляется не только качественное понимание, но и попытка описать ко­личественные характеристики опытных данных. В принципе к тому же стремится и теория, и различие между теорией и моделью, как я уже подчеркивал, состоит в том, что модель не выводится из наибо­лее полной теории, а как бы пристраивается к ней внешним образом. Как правило, такие модели носят очень феноменологический харак­тер (вспомним понятие феноменологической теории) и основываются на использовании аналогий.

Очень хорошим примером такого рода моделей является гидро­динамическая модель множественного рождения частиц при очень высоких энергиях, предложенная В. Гейзенбергом. В этой модели сталкивающиеся частицы рассматриваются как сгустки некоего мало определенного субстрата конечного размера, которые в силу реляти­вистского сокращения имеют вид плоских дисков. При столкновении дисков происходит сильное сжатие этого субстрата, как если бы он был сжимаемой жидкостью. А затем этот объединенный сжатый сгу­сток начинает расширяться и распадается на множество фрагментов, которые ведут себя как жидкость, описываемая уравнениями гидро­динамики с вязкостью.

В этой модели очень хорошо видны такие черты, как феноменоло-гичность и невыводимость из основных уравнений фундаментальной теории. Такого рода модели достаточно часто используются в физике, при этом ученые надеются, что в дальнейшем им будет дано более строгое обоснование.

3.3.5. Метод мысленного эксперимента

Метод мысленного эксперимента, как и метод математического эксперимента, относится к числу тех методов, о которых слушатели всегда спрашивают: а почему мы не рассматриваем их, когда обсуж­даем метод эксперимента в научном познании вообще. Ответ состоит в том, что метод эксперимента относится к эмпирическому уровню научного познания, тогда как указанные методы относятся полно­стью к теоретическому уровню, и слово «эксперимент» в их названии должно стоять в кавычках.

Метод мысленного эксперимента используется в теоретической познавательной деятельности очень давно. Первым примером исполь­зования метода мысленного эксперимента, который мне удалось об­наружить, являются апории Зенона Элейского, особенно об Ахиллесе и черепахе. Зенон ведь не экспериментировал с реальным Ахиллесом и реальной черепахой. Зеноновы «Ахиллес» и «черепаха» — это абст­рактные понятия. И Зенон мысленно оперирует этими понятиями.

Можно найти еще несколько примеров использования такого типа рассуждений в античную эпоху. Наиболее интересными и значимы­ми являются мысленные эксперименты Архимеда, направленные на


125

установление законов равновесия тел. Архимед прибегал к приему мысленного взвешивания частей тела.

Вообще, можно думать, что в античную эпоху этот метод имел широкое распространение, но, видимо, большинство таких рассуж­дений до нас не дошло. Поэтому основной областью, на которой мож­но выявить действенность метода, является наука Нового времени.

Метод мысленного эксперимента сыграл исключительно важную роль во всем развитии Науки, начиная с XVII века и вплоть до се­редины XX. Многие мысленные эксперименты стали эпохальными в развитии науки и получили имена собственные — демон Максвелла, поезд Эйнштейна, лифт Эйнштейна, микроскоп Гейзенберга.

Объем нашего курса ограничен, и я не смогу рассмотреть все мыс­ленные эксперименты, которые сыграли существенную роль в исто­рии физики.

Первыми такими экспериментами в науке Нового времени ста­ли мысленные эксперименты Г. Галилея. Первый из них относился к установлению первого закона Ньютона. Г. Галилей рассматривал поведение тележки на наклонной плоскости: если тележка катится вверх, то ее скорость уменьшается, а если она катится вниз, то ско­рость растет. А что будет на абсолютно горизонтальной плоскости? Поскольку горизонтальная плоскость есть нейтральное состояние, то скорость должна сохраняться. И таким образом Галилей приходит к качественному пониманию закона инерции. Второй мысленный эксперимент Галилея — эксперимент с «мухами». Галилей рассмат­ривает поведение роя «мух», выпущенных из коробки, в неподвиж­ной комнате и в каюте движущегося корабля и приходит к принципу относительности механического движения.

Если в мысленном эксперименте с тележкой на плоскости еще можно подозревать нечто близкое к реальному эксперименту, то во втором случае такое подозрение можно сразу отбросить. Ясно, что Галилей не ловил мух, не запирал их в ящик и не выпускал ни на су­ше, ни на море. Это именно мысленное оперирование, и не мухами, а понятиями.

Теперь я пропущу два столетия и перейду сразу к XIX веку. Имен­но тогда метод мысленного эксперимента достиг расцвета и дал ис­ключительно богатые результаты.

Одним из наиболее значительных мысленных экспериментов XIX века был знаменитый цикл Карно. Цикл Карно — это очень хоро­ший и очень показательный пример. Действительно, Никола Леонард Сади Карно (1796—1832) не экспериментировал ни с какой реальной тепловой машиной, он не использовал никаких реальных рабочих тел. Он осуществлял все эти действия мысленно. Напомню, что цикл Кар­но состоит из четырех стадий — двух изотерм и двух адиабат, которые образуют замкнутый цикл, чтобы машина не просто сработала один раз и остановилась, но могла осуществлять периодическую работу. Обратите внимание — нам все известно и про каждую изотерму и про

126


каждую адиабату, но каков окончательный результат! Я думаю, что всем вам ясно эпохальное значение цикла Карно — он стал началом всей термодинамики в целом и ее второго закона в частности (если это можно назватьчастностью).

Но значение цикла Карно состоит не только в том эпохальном результате, который был получен с его помощью. Цикл Карно стал началом метода, который очень широко использовался в термоди­намике XIX — начала XX века. Суть метода состояла в том, что для решения какой-либо термодинамической, а иногда и выходящей за рамки термодинамики задачи строился специально цикл типа цикла Карно.

Именно так было получено известное уравнение Клапейрона-Клау-зиуса для зависимости давления насыщенного пара от температуры

— = Х-~ dT RT²'

где А. — теплота испарения. При получении этого уравнения рассмат­ривался цикл Карно, в котором рабочим телом является насыщен­ный пар.

Впоследствии точно так же было впервые получено уравнение для зависимости тока термоэлектронной эмиссии от температуры. Только там в качестве рабочего тела рассматривался электронный газ, «ис­парявшийся» из эмиттера.

Специальный интерес представляет мысленный эксперимент Бартолли — Больцмана. В этом «эксперименте» рабочим телом для цикла Карно являлось излучение черного тела, и результат состоял в том, что для того чтобы выполнялся второй закон термодинамики, необходимо, чтобы излучение обладало давлением. Таким образом, еще до опытов Петра Николаевича Лебедева (1866-1912), световое давление было дважды предсказано теоретически — Дж. Максвел­лом из электродинамического расчета и Адольфо Бартолли (1851-1896), и Людвигом Больцманом (1844-1906) на основании метода циклов.

В свое время, когда я работал над этой темой, я прочитал книгу Вальтера Фридриха Германа Нернста (1864-1941) «Основы теоре­тической химии», изданную в 1906 г. (на немецком языке). В ней все соотношения химической термодинамики выводятся на основе метода циклов.

Эффективность метода циклов Карно привела к распространению его по аналогии и на други области. Так, основатель физической хи­мии Якоб Хендрик Вант-Гофф (1852-1911) для рассмотрения проблем химического равновесия реакций применил мысленный эксперимент, который называется «ящик обратимости Вант-Гоффа». А в начале нашего века при рассмотрении энергий связи молекул и кристаллов очень активно использовался метод энергетических циклов Борна— Габера.


127

Рассмотрим цикл Борна-Габера на простейшем примере опреде­ления энергии связи (энергии диссоциации) ионной молекулы А⁺В~. Составим цикл из нескольких этапов:



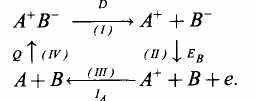
На первом этапе молекула А⁺В~ разделяется на ионы А⁺ и В , для чего требуется затратить энергию диссоциации D. На втором этапе у иона В~ отнимается электрон и затрачивается энергия Е_в — сродство к электрону атома В или энергия «ионизации» иона В~, определяе­мая спектроскопически. На третьем этапе электрон соединяется с ионом А⁺, и выделяется энергия 1_А — энергия ионизации атома А, определяемая спектроскопически. На четвертом этапе атомы А и В вступают в химическую реакцию с выделением теплоты реакции Q, определяемой калориметрически. В силу закона сохранения энергии пишем уравнение

-D-E_B+I_A+Q = 0 D = Q + I_A-E_B.

Чрезвычайно важную роль сыграл в развитии физики XIX века мысленный эксперимент, известный под названием «демон Максвел­ла». Я не буду его описывать, поскольку вы все его знаете. Обращу только ваше внимание на то, что это вовсе не эксперимент в смыс­ле эмпирического познания, а именно теоретическое рассуждение. Очевидно, что Дж. Максвелл не экспериментировал с заслонками на пружинках и все элементы этого «эксперимента» именно мысленные. И еще хочу напомнить вам о том, какой мощный толчок развитию молекулярной физики дал «демон Максвелла».

Не менее активно, чем в XIX веке, мысленный эксперимент ис­пользовался в XX веке. Этот метод сыграл очень важную роль в созда­нии специальной, а затем и общей теории относительности. В первом случае весьма широко известен мысленный эксперимент — «поезд Эйнштейна». А. Эйнштейн рассматривал поезд, проезжающий мимо неподвижной платформы. В два конца поезда ударяют молнии, и эти два события будут одновременны для наблюдателя на платформе и не­одновременны для наблюдателя на поезде. Тем самым Эйнштейн де­монстрирует относительность понятия одновременности.

При создании общей теории относительности А. Эйнштейн исполь­зовал мысленный эксперимент «лифт». Он рассматривал процессы в свободно падающем лифте и пришел к выводу о том, что ускорен­ное движение локально эквивалентно однородному гравитационно­му полю, т. е. сформулировал очень важный в ОТО принцип экви­валентности.





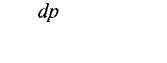
128


И вообще, в своем научном творчестве А. Эйнштейн очень часто использовал метод мысленного эксперимента, но об этом я скажу чуть позже.

Второй областью науки XX века, в которой очень большую роль сыграл метод мысленного эксперимента, является квантовая меха­ника. Я хочу рассказать вам о замечательном мысленном экспери­менте — «микроскопе Гейзенберга».

Пусть мы хотим определить координату электрона. Ясно, что ли­нейку использовать нельзя, поскольку риска линейки не может быть меньше размера атома. Микрометром тоже электрон не зажмешь. Но можно использовать рассеяние света на электроне — эффект Ком-птона. Осветим электрон светом, соберем рассеянный электроном свет при помощи «микроскопа» на экран.

На экране появится световая точка. И теперь, зная пложение точ­ки и параметры микроскопа, можно найти координату электрона.



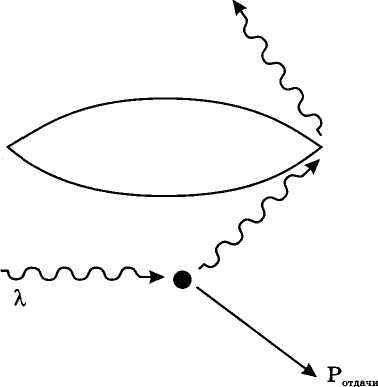
Рис. 1-7.

Далее учтем, что в силу дифракции света на краю линзы на экране будет не точка, а конечное пятно размером порядка X. Следовательно, координата электрона будет измерена с неопределенностью

Дх~А..

Для того, чтобы уменьшить Ах, нужно уменьшить X.

Теперь примем во внимание, что при рассеянии света на электроне электрон получает импульс отдачи и, следовательно, возникает неоп­ределенность импульса порядка импульса самого фотона:


129

А теперь перемножим эти два соотношения и получим

Ах Ар = П.

Вы видите — тривиальный рисунок, две строчки, а каков резуль­тат! Именно так впервые было получено соотношение неопределен­ностей. Сейчас вы его получаете, делая разложение волнового пакета в интеграл Фурье или вычисляя коммутатор некоммутирующих опе­раторов. Но впервые соотношение неопределенностей было получено именно при помощи «микроскопа Гейзенберга». И опять я хочу под­черкнуть чисто теоретическую природу этого рассуждения.

Вообще, развитие квантовой механики, а затем и квантовой тео­рии поля было очень сильно связано с методом мысленного экспе­римента. Широко известна дискуссия А. Эйнштейна и Н. Бора по познавательным проблемам квантовой механики в 1927 году. А. Эйн­штейн при помощи очень остроумных мысленных экспериментов пытался доказать противоречивость квантовой механики, а именно, что можно получить знание о параметрах микрообъекта, выходящее за пределы точности, допускаемой соотношением неопределенностей. И каждый раз Н. Бор обнаруживал некорректность в рассуждениях А. Эйнштейна, состоящую в использовании чрезмерных абстракций. Но структура мысленных экспериментов Эйнштейна оказалась такой интересной, что последний из них, Бор, продолжал осмысливать ее вплоть до своей смерти.

В начале 30-х годов А. Эйнштейн признал непротиворечивость квантовой механики, но поставил своей задачей доказать ее непол­ноту. Знаменитая статья Альберта Эйнштейна, Бориса Подольского (1896-1966) и Натана Розена (1909-1995) «Является ли квантовая механика полной?» включает мысленный эксперимент, результатом которого является знаменитый парадокс Эйнштейна-Подольского-Розена (парадокс ЭПР). Обсуждение этого парадокса продолжается до настоящего времени.

Последними в этом ряду были мысленные эксперименты Бора—Ро-зенфельда и Ландау—Пайерлса, посвященные проблеме измеримости полей в квантовой теории поля.

Итак, метод мысленного эксперимента сыграл выдающуюся роль во всем развитии науки, начиная с XVII века. Методологическое ос­мысление метода мысленного эксперимента началось в начале наше­го века в рамках философского направления — второго позитивиз­ма, в работах крупнейших его представителей Э. Маха и П. Дюгема. Именно в их работах сформировались два основных понимания ме­тода. Первое понимание можно назвать «экспериментистским». Оно берет начало от Маха. В этом понимании мысленный эксперимент рассматривается как продумывание реального эксперимента или даже как замена реального эксперимента.

Можно сказать больше. С точки зрения общей позиции Маха, в ко­торой единственная реальность — это та, которая существует в нашем сознании, вообще нет разницы между мысленным экспериментом







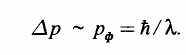
130


и реальным. Мысленный эксперимент существует в сознании уче­ного, но и реальный тоже существует в сознании. Сам Мах не делал столь откровенного заявления, хотя оно очень четко следует из его общефилософской позиции. Но существенное сближение мысленного и реального эксперимента он все же проводил.

Нельзя сказать, что Э. Мах полностью не прав. Некоторые мыс­ленные эксперименты действительно напоминают схематическое продумывание реального эксперимента. Однако если брать ситуацию в целом, то, конечно же, мысленный эксперимент только весьма отда­ленно связан с реальным. Совершенно очевидно, что если бы С. Карно попытался экспериментировать с реальными тепловыми машинами, он никогда бы не получил КПД сколько-нибудь близкий к теоретиче­скому значению. Ясно, что никто и никогда не будет строить тепловой двигатель с электронным газом или излучением в качестве рабочего тела, и тем более невозможно строить «демон Максвелла» с заслон­ками и пружинками.

Следовательно, точка зрения П. Дюгема полностью оправдана. Последний настаивал на теоретической природе мысленного экспери­мента. Он указывал, что результат мысленного эксперимента зависит от принципа. И правильность результата мысленного эксперимента зависит от правильности принципа, причем эта правильность долж­на быть проверена реальным экспериментом. Эту позицию можно назвать «теоретистской».

Несмотря на то, что «теоретистская» позиция была выдвинута и обоснована П. Дюгемом еще в начале века, «экспериментистская» позиция получила довольно значительное развитие. В ряде работ 60-х — 70-х годов утверждалось, что мысленный эксперимент эф­фективен в тех ситуациях, когда реальный эксперимент трудно вы­полнить, т. е. мысленный эксперимент является заменой реального. В качестве аргумента сторонники «экспериментистской» точки зре­ния приводят то обстоятельство, что в мысленных экспериментах мы получаем новое знание.

Этот аргумент явно несостоятелен. Напомню, что новое знание получается не только на эмпирическом уровне, но и на теоретиче­ском. В XVIII веке в этом еще можно было сомневаться, но в XIX и XX веках получение нового знания на теоретическом уровне — явление вполне обычное. Это всем известные теоретические предска­зания, которые в XIX веке метафорически называли «открытиями на кончике пера». В XX веке они стали заурядными. И ссылаться на получение нового знания как на доказательство экспериментальной природы мысленного эксперимента есть просто недомыслие.

Итак, мысленный эксперимент есть метод теоретического уровня научного познания. Но это решение не снимает проблемы сущности метода. Проблема состоит в том, что еще неясно, чем именно мыс­ленный эксперимент как особый метод выделяется на теоретическом уровне.


131

В ряде работ выдвигалась точка зрения, что мысленный экспери­мент выделяется тем, что он оперирует идеализированными объек­тами. Я думаю, что это не решает проблемы специфики мысленного эксперимента, — любая теория оперирует идеализированными объ­ектами. Это одна из обязательных черт теории. Так что использова­ние идеализированных объектов не может считаться спецификой мысленного эксперимента. Это, скорее, показатель теоретической природы данного метода.

Еще одна точка зрения состоит в том, что сущность метода мыс­ленного эксперимента состоит в использовании наглядных образов. В связи с этим даже делалась попытка сформулировать «принцип наглядности». Я думаю, что эта позиция также неверна. Какой на­глядностью обладает, например, цикл Карно? Но все же в этой точке зрения есть «рациональное зерно». Дело в том, что в методе мыс­ленного эксперимента используются не столько наглядные, сколько очень упрощенные ситуации — модели, т. е. метод мысленного экс­перимента очень тесно связан с методом моделирования, естественно, на теоретическом уровне научного познания.

С модельным характером мысленного эксперимента связано то обстоятельство, что этот метод очень принципиально использует абст­ракцию потенциальной осуществимости. Так, в «демоне Максвелла» фигурирует «заслонка на пружине», способная пропускать одну мо­лекулу. Ясно, что осуществить подобную «пружинку» можно только в абстракции. Или, например, в мысленных экспериментах, обсуж­давшихся во время дискуссии А. Эйнштейна и Н. Бора, рассматри­вается дифракция электрона на двух щелях. Совершенно очевидно, что в реальности нельзя сделать щель, пригодную для наблюдения дифракции электронов. Щель для наблюдения дифракции должна иметь неоднородность края, существенно меньшую длины волны. Но неоднородность края щели реально не может быть меньше размеров атома. Так что щель, пригодная для наблюдения дифракции элек­тронов, есть абстракция.

Именно такого рода абстракции и являются абстракциями потен­циальной осуществимости. И вот тут оказывается, что с такого рода абстракциями нужно оперировать осторожно. Далеко не любая абст­рактная ситуация может быть квалифицирована как потенциально осуществимая. Именно это обстоятельство является критерием для определения корректности мысленного эксперимента.

Можно выделить два признака корректности. Первый из них со­стоит в том, что действие, осуществляемое в мысленном эксперимен­те, должно иметь достаточно хорошую определенность. В научных мысленных экспериментах это требование всегда (я не знаю исключе­ний) выполняется. Но в ненаучных рассуждениях очень часто можно отметить его нарушение.

Так, рассуждение Дж. Беркли о вишне, у которой отнимаются вто­ричные качества, представляет собой пример философского мыслен-

132