1 Проблема познаваемости мира в истории философии

Вид материала

Документы

Подобный материал:

• «Проблема взаимоотношения человека и мира в социальной онтологии», 368.23kb.
• Темы рефератов диалектическая, метафизическая и креационистская модели развития мира, 52.45kb.
• Проблема жизни, смерти, бессмертия мира, человечества, человека в контексте истории, 302.24kb.
• Нп «сибирская ассоциация консультантов», 206.84kb.
• Вопросы к зачету по курсу «история философии в украине», 20.13kb.
• Проблема реализма и основные концепции соотношения языка и реальности в аналитической, 579.92kb.
• Учебно-методический комплекс специального курса «Проблема человека в Древнегреческой, 209.13kb.
• Учебно-методический комплекс специального курса «Проблема человека в Древнегреческой, 256.77kb.
• Программа минимум кандидатского экзамена по специальности 09. 00. 03 «Истории философии», 494.66kb.
• Проблема следования правилу как проявление радикального эпистемологического скептицизма, 547.43kb.

Г

ного эксперимента. Напомню, что Беркли стремился доказать несу­ществование каких-либо объектов вне нашего сознания. Для этого он использовал локковскую концепцию первичных и вторичных качеств. Первичные качества — это такие, которыми объект обладает сам по себе, независимо от других объектов, в том числе и от человеческого восприятия. Вторичные качества, по Локку, — это такие, которые появляются, возникают в результате воздействия объекта на органы чувств человека и существуют только в сознании субъекта. Так, цвет, вкус, запах и прочее есть именно результат такого воздействия и не присущи объекту самому по себе. И далее возникает вопрос: что ста­нет с объектом, если у него последовательно отнимать все вторичные качества? Например, у вишни отнимать последовательно цвет, вкус, запах, плотность? И далее Беркли отвечает, что если у объекта отнять последовательно все вторичные качества, т.е. воспринимаемые чело­веком, то он перестанет существовать: «существовать — значит быть воспринимаемым». Но, поскольку восприятия человека существуют только в его сознании, то и сами объекты тоже существуют только в человеческом сознании.

Легко видеть, что рассуждение Беркли представляет собой ти­пичный мысленный эксперимент. Современникам Дж. Беркли его рассуждение представлялось весьма основательным. Но давайте поставим вопрос: корректен ли мысленный эксперимент Беркли? Я отвечаю — нет. Он некорректен, поскольку используемые в нем абстракции не определены. Что означает «отнять у вишни цвет»? Пе­рекрасить ее, что ли? Но это явно абсурдно. Поэтому я утверждаю, что абстракция «отнимания цвета» — пустая (может быть реализована только на пустом множестве). Я знаю, что значит лишить человека зрения — это пожалуйста, но что такое «отнять цвет» — это никому, в том числе и самому Беркли, неизвестно. Так что мысленный экспе­римент Беркли некорректен.

Справедливости ради хочу сказать, что сама постановка вопроса о корректности мысленного эксперимента возникла только в начале XX века — через полтораста лет после смерти Беркли.

Но я мог бы привести и более «свежие» примеры. Так, в школе «деятельности», о которой мы говорили в начале курса, использо­вался мысленный эксперимент с негеоцентрическим существом раз­мером 10¹⁰⁰ см — для сравнения, предполагаемый размер Вселенной всего 10⁴⁰ см. И далее утверждалось, что для такого субъекта не будет существовать ни Луны, ни Земли, ни даже Солнца, поскольку в силу своей малости они не могут войти в его деятельность.

Это опять мысленный эксперимент, и он основан на абстракции потенциальной осуществимости сколь угодно большого увеличения размера мыслящего существа. При этом утверждалось, что филосо­фия не должна бояться таких абстракций. И я опять хочу обратить ваше внимание на то, что абстракция существа 10¹⁰⁰ см не опреде­лена. Лучшим доказательством пустоты этой абстракции является


133

контррассуждение. У существа с размером 10¹⁰⁰ см и разрешающая способность глаза возрастет настолько, что оно будет просто видеть не только Луну или Землю, но даже атомы и электроны.

Я думаю, вам понятно, что коль скоро из некоторой абстракции получаются противоречивые выводы, то и сама она либо противоре­чива, либо пуста, т. е. не определена.

Значит, первым условием корректности мысленного эксперимента является достаточная определенность абстракции потенциальной ' осуществимости так, чтобы она не была пустой.

Но есть и второе условие. Оно состоит в том, что абстракции, ис­пользуемые в мысленном эксперименте, должны быть согласованы между собой. Так, в мысленных экспериментах Эйнштейна, исполь­зованных им в дискуссии с Бором, рассматривалось квантовое пове­дение (дифракция) электронов на двух щелях, и каждая щель была полуприкрыта заслонкой, ведущей себя классически. Бор указал на эту непоследовательность — заслоночку нужно тоже рассмат­ривать как квантовый объект. Если этого не сделать, то результат мысленного эксперимента будет противоречивым, что и получилось у Эйнштейна.

Итак, мысленные эксперименты представляют собой модели, ос­нованные на абстракции потенциальной осуществимости, но эти аб­стракции не могут быть произвольными. Они должны удовлетворять условиям непустоты класса объектов и согласованности.

Но все же это еще не дает полного ответа на вопрос о специфике ме­тода мысленного эксперимента. Остается непроясненным механизм получения нового знания.

Я предлагаю вашему вниманию следующую точку зрения — осно­вой для получения нового знания в мысленном эксперименте являет­ся требование системности, целостности, согласованности.

Мы проделываем мысленно, основываясь на абстракции потен­циальной осуществимости, ряд этапов — действий, процессов — по­следовательно или параллельно и требуем, чтобы они образовывали целостную систему. В результате мы получаем новое знание. Можно указать несколько вариантов этого механизма.

Первый состоит в том, что мы знаем все о каждом этапе. Тогда ре­зультатом будет знание о том, в силу какого требования эти этапы об­разуют целостность. Например, в цикле Карно мы знаем все о каждой изотерме и каждой адиабате, но не знаем, каково условие целостности цикла. Таким условием целостности является формула Карно для КПД или, шире и фундаментальнее, — второй закон термодинамики.

Аналогичная ситуация имеет место в «микроскопе Гейзенберга» — мы знаем все об эффекте Комптона (рассеянии света на электроне) и все о дифракции света. Но мы не знаем, каковы условия одновре­менной применимости волновых и корпускулярных представлений. Соотношение неопределенностей как раз и представляет это условие целостности, одновременной их применимости.

134


Г

Другой вариант состоит в том, что мы знаем общий принцип це­лостности, но не знаем характеристики какого-либо этапа или усло­вия связи между этапами. Тогда новое знание и представляет собой искомую характеристику. Так функционируют все методы циклов. В циклах типа Карно мы знаем основной принцип целостности — вто­рой закон термодинамики. Но в случае вывода уравнения Клапейро­на—Клазиуса не знаем, как зависит давление насыщенного пара от температуры, а в случае мысленного эксперимента Бартолли-Больц-мана, какой-то характеристики излучения как рабочего тела. В ре­зультате мысленного эксперимента мы устанавливаем неизвестную нам связь или характеристику.

Точно так же «работает» метод энергетических циклов. В нем принципом целостности является закон сохранения энергии.

И, наконец, может быть специальный вариант, когда в результате мысленного эксперимента мы обнаруживаем внутреннее противоре­чие в нашем знании. Этот случай родственен первому, но здесь мы не достигаем знания принципа целостности, а только констатируем наличие противоречия. Эта ситуация реализуется в «демоне Максвел­ла» . Этот мысленный эксперимент установил противоречие между элементарно понимаемой молекулярно-кинетической теорией и вто­рым законом термодинамики. Как вы знаете, это противоречие было ликвидировано на основе развития теории флуктуации. Аналогичная ситуация имела место в мысленных экспериментах Эйнштейна в дис­куссии с Бором. Эйнштейн пытался установить противоречивость квантовой механики. Но Бор показал противоречивость самого мыс­ленного эксперимента Эйнштейна.

Такова, по моему мнению, сущность мысленного эксперимента как особого метода теоретического уровня научного познания.

Как вы видите, мысленные эксперименты сыграли выдающуюся роль в развитии физики, и в особенности физики XIX и XX веков.

Но необходимо отметить, что во второй половине XX века мы не имеем столь выдающихся примеров. Более того, все те результаты, которые раньше получались при помощи мысленных эксперимен­тов, сейчас предпочитают получать при помощи строгих математи­ческих выводов. Так, все результаты, которые раньше получались при помощи метода термодинамических циклов, сейчас выводятся при помощи уравнений для термодинамических потенциалов. Метод циклов сохраняется только в учебниках, и то не во всех. Соотношение неопределенностей сейчас даже в учебниках получают не при помощи «микроскопа Гейзенберга», а путем вычисления коммутатора опера­торов. И так везде — метод мысленного эксперимента вытесняется формализованным выводом.

Метод мысленного эксперимента перешел из научных работ в эв­ристическое мышление естествоиспытателей, в кулуарные споры. И возможно, уже навсегда.


135

Конечно, было бы очень жаль, если бы метод, имеющий столь ве­ликое прошлое, ушел из науки. Но факт остается фактом — с конца 30-х годов в науке нет таких замечательных примеров применения мысленного эксперимента.

3.3.6. Метод математического эксперимента

Последний метод, который я хочу рассмотреть в данном разде­ле учебного пособия, — это метод математического или численного эксперимента. Еще раз повторю, что этот метод не имеет никакого отношения к эмпирическому эксперименту.

Численный эксперимент состоит в том, что мы решаем уравнения какой-то теории или модели на машине. Обычно это делается много раз, с изменением входящих в уравнение параметров или даже с отбрасы­ванием или включением в уравнения дополнительных членов.

Но ведь это ничем не отличается от того, что теоретики делают поч­ти триста лет. Теоретики всегда решали уравнения и всегда меняли значения параметров и даже вид уравнения.

Правда, теоретики обычно стремились получить аналитическое ре­шение не с фиксированным, а с общим видом параметра (в виде неоп­ределенного символа), а затем исследовать характер зависимости от параметра. Но это никак не меняет принципиальной ситуации. Дело в том, что когда теоретики не могут получить аналитическое решение, точное или приближенное, то они решают уравнение численно. И это было всегда. Напоминаю всем, что методы численного решения диффе­ренциальных уравнений Эйлера или Рунге-Кутта были разработаны, когда еще никаких машин не существовало, и были созданы именно для решения «руками». Так что никакого принципиального отличия нет.

Когда же для обоснования «экспериментальной» сущности мето­да ссылаются на то, что с его помощью могут быть получены новые неожиданные результаты, то это просто недомыслие (даже если его высказывает какой-нибудь академик). Новый результат, полученный методом математического «эксперимента», — это нормальное теоре­тическое предсказание. И мы уже неоднократно рассматривали это, конечно же, исключительно важное свойство теории. Причем, как всякое теоретическое предсказание, предсказание математического «эксперимента» требует проверки настоящим экспериментом. И ни­чего принципиально нового и интересного в этом аспекте нет.

То, что я только что сказал, не означает, что метод математического (или численного) эксперимента вообще не представляет методологиче­ского интереса — напротив, как метод теоретического уровня научного познания он обладает своей спецификой, заслуживающей внимания.

Я не являюсь специалистом в этой области и не претендую на дос­таточно полный анализ проблем, связанных с осмыслением метода математического эксперимента. Но я могу сказать, что большинство работ на эту тему представляет собой сплошное пустословие на тему «ах, как хорошо, что можно получить новый результат!» или пересказ

136


Г

конкретных приемов вычислении или результатов, полученных в ре­зультате вычислений. И ничего философского или методологического в этих работах нет, хотя претензии были очень большими.

Что же можно все же выделить в качестве специфики математи­ческого «эксперимента» как особого метода? Я думаю, что в первую очередь следует выделить интересный и важный момент: когда мы по­лучаем множество численных частных решений, то мы можем их про­анализировать, выделить некоторые общие черты частных решений и произвести обобщение. Иначе говоря, мы включаем очень активно метод индукции. Раньше основной областью применения метода ин­дукции было обобщение единичных эмпирических данных в эмпири­ческие закономерности, теперь же мы можем обобщать частные, но тео­ретические решения. Может быть, именно это сходство и послужило основанием называть данный метод математическим экспериментом.

Вторым интересным аспектом (но он очень тесно связан с первым) является то, что, анализируя и обобщая частные решения, мы можем угадать способ аналитического получения результата. В качестве при­мера приведем следующую ситуацию.

Я думаю, что вы слышали о числе Фейгенбаума. Это число име­ет следующий смысл. Рассмотрим отображение единичного отрезка в себя, задаваемое выражением

*„₊₁ = *■/(*»)

Процесс отображения имеет периодический характер. Если изме­нять значение X, то при некоторых критических значениях X проис­ходит удвоение периода. Если выписать эти критические значения X_v Х₂, ... то оказывается, что они образуют сходящуюся последователь­ность, и пределом этой последовательности является новое (кроме общеизвестных тг и е) трансцендентное число, называемое числом Фейгенбаума. Так вот, первоначальные результаты были получены Митчелом Фейгенбаумом именно при помощи численного расчета. И только потом, на основе осмысления и обобщения результатов рас­чета, было найдено аналитическое решение.

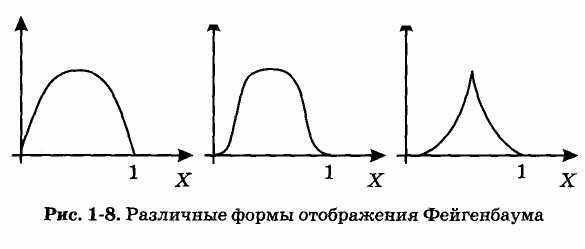
Кстати, число Фейгенбаума не одно, их много, и они зависят от вида функции отображения (см. рис. 1-8).

1 J J


137

Возможно, существуют какие-нибудь еще интересные аспекты применения метода математического «эксперимента», но я о них просто не знаю.

А теперь рассмотрим некоторые трудности метода.

Когда мы решаем теоретические уравнения аналитически, точно или каким либо приближенным методом (скажем, методом теории возмущений), и обнаруживаем расхождение с реальным эксперимен­том, то источником этого расхождения могут быть несовершенство используемой теории (полной теории, приближенной теории и моде­ли) или несовершенство приближенного метода решения. В случае использования теории возмущений мы, как правило, не можем на­писать выражение для общего вида членов ряда теории возмущений и просуммировать его. В таких случаях мы ограничиваемся одним, двумя, тремя членами ряда. При этом возникают проблемы оценки неучтенных членов, сходимости ряда и прочие.

Все эти проблемы возникают и при численном решении. Но кроме этих, при использовании численных решений возникает еще одна. Любое численное решение проделывается с точностью до очень ма­лой, но конечной ошибки вычисления. И вот эти малые ошибки вы­числения могут накапливаться. В итоге в окончательном решении ошибка может стать очень большой. Я помню, как в конце 60-х годов у нас в Физтехе проводились расчеты спускаемых космических ап­паратов. При этом куда-то девалась половина энергии. Я не большой знаток современной ситуации, но, насколько мне известно, поло­жение дел изменилось не слишком сильно. Точность вычислений машин возросла (ошибка вычисления стала меньше), но возросла и сложность решаемых задач. Так что результат накопления ошибок вычисления по-прежнему может оказаться очень большим. И основ­ная трудность состоит в неконтролируемости процесса накопления ошибок.

Эту трудность пытаются преодолевать использованием так назы­ваемых тест-задач, т. е. таких задач, которые имеют точное реше­ние. Это точное решение сравнивают с численным решением и таким образом оценивают качество вычислительной процедуры. По сути дела, тест-задачи являются моделями для вычислительных процедур, и метод тест-задач является методом моделирования по отношению к программам. Однако и здесь есть существенный момент ненадеж­ности. Если программа хорошо работает в задачах одного типа, то в задачах другого типа может начаться накопление ошибок.

Таким образом, метод математического или вычислительного «эксперимента» обладает как несомненными методологическими достоинствами, так и своими специфическими недостатками.

Мы рассмотрели ряд методов научного познания как на эмпири­ческом, так и на теоретическом уровнях.

И теперь возникает вопрос — что это? — просто совокупность прие­мов, более или менее эффективных в процессе научного познания, или





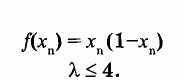
138


Г

же это нечто большее, не просто методы, а научный метод? Имеется ли в нем внутреннее единство, которое позволяет его так называть?

Я намерен защищать и обосновывать именно эту точку зрения. И прежде всего я хочу обратить ваше внимание на весьма явную внут­реннюю связь между различными методами. Вспомните, сколько раз при рассмотрении какого-либо одного метода нам приходилось обра­щаться к результатам анализа других методов: индукция — гипоте­за — аналогия, модель — мысленный эксперимент, математический эксперимент — индукция.

Но эта связь между методами — не самое важное, хотя, конечно, и она интересна в аспекте выявления единства научного метода. Более важным мне представляется ответ на вопрос: существует ли во всех этих методах некий инвариант, жесткое ядро, то, что объединяет их в единую целостность, которую мы называли научным методом, единым для всей науки и создающим единство самой науки?

Я отвечаю на этот вопрос положительно — да, такое жесткое инва­риантное ядро существует! Этим ядром являются методологические принципы научного познания.

Изучение этих принципов и является предметом следующей части нашего курса.