Методика обучения детей старшего дошкольного возраста измерению объемов сыпучих и жидких веществ с помощью условной меры. Формирование представлений старших дошкольников о массе и способах ее измерения

Вид материала

Документы

Содержание Роль математических знаний С понятием умственных способностей тесно связано понятие «математические способности» - это такие специфические особенности мысл 2. Освоение логических операций мышления, которые включаются в процесс овладения математическим содержанием. 3. Усвоение и расширение словарного запаса, совершенствование грамматического строя и связности речи. Разработка вопросов формирования математических представлений в трудах отечественных педагогов. Величина, форма Задачи: сложение и вычитание на конкретном материале.Дидактический материал для развития органов чувств. Младшая группа Средняя группа Старшая группа Взгляды на математическое развитие Дидактические средства 1. демонстрационный 2. раздаточный Сюда относятся Методика работы по формированию представлений Организуя работу Возможные ошибки детей при измерении объемов Формирование у дошкольников представлений Физическая величина, пропорциональная отношению величины действующей на тело силы к сообщаемому ей ускорению, называется массой Структура «идеального действия» по обследованию тяжести ... Полное содержание

Подобный материал:

• Методика обучения детей дошкольного возраста основным видам движений. Организация, 52.9kb.
• Особенности восприятия у детей старшего дошкольного возраста особенности восприятия, 146.11kb.
• Автор: Одинцова Надежда Юрьевна, воспитатель мдоу №27 г. Оренбурга Представлено: Колисниченко, 686.94kb.
• Программа дисциплины «Теория и методика развития элементарных математических представлений, 244.08kb.
• Й курс специальности «Дошкольная педагогика и психология» (дневное отделение) и «Педагогика, 53.21kb.
• Предмет исследования комплекс специальных психолого-педагогических упражнений по развитию, 17.37kb.
• Рабочая программа по курсу " Теория и методика развития математических представлений, 118.95kb.
• Игра как средство умственного развития детей среднего дошкольного возраста., 49.4kb.
• Влияние дидактических игр на развитие цветовосприятия дошкольников, 17.06kb.
• План Актуальность проблемы формирования начал экологической культуры у детей старшего, 137.98kb.

Государственное образовательное учреждение

среднего профессионального образования

Педагогический колледж № 4 Санкт-Петербурга


УЧЕБНО-МЕТОДИЧЕСКИЕ

И ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ

ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

ПО КУРСУ

«МЕТОДИКА МАТЕМАТИЧЕСКОГО РАЗВИТИЯ

ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА»


для студентов очно-заочного отделения


преподаватель Е.В.Семёнова


2008


Содержание самостоятельной работы студентов

по курсу "Методика математического развития

детей дошкольного возраста"

отделения очно-заочного обучения

1. Роль математических знаний в умственном развитии детей дошкольного возраста.
   
2. Математическое развитие ребенка дошкольного возраста по методу Е.И.Тихеевой и Ф.Н.Блехер.
   
3. Разнообразие дидактических средств математического развития дошкольников. Требования к отбору и конструированию дидактических средств.
   
4. Понятие времени, ориентировки во времени. Особенности восприятия времени детьми разного возраста.
   
5. Современные дидактические средства математического развития дошкольников: значение и место в образовательном процессе (на примере развивающих игр, блоков Дьенеша, палочек Кюизенера и др.).
   
6. Методика обучения детей старшего дошкольного возраста измерению объемов сыпучих и жидких веществ с помощью условной меры.
   
7. Формирование представлений старших дошкольников о массе и способах ее измерения.
   
8. Воссоздание образных и сюжетных изображений из геометрических конструкторов типа "Танграм": значение и методика этой работы.
   
9. Методика обучения детей ориентировке в пространстве в разных возрастных группах.
   
10. Использование игр на пространственное моделирование в работе по формированию пространственных представлений.
    
11. Методика обучения порядковому счету. Специфика задач и приемов работы в среднем и старшем дошкольном возрасте.
    
12. Методика использования различных анализаторов при обучении счету и формировании представлений о числах и отношениях между ними.
    
13. Приемы работы по ознакомлению старших дошкольников с составом чисел первого десятка из единиц и двух меньших чисел.
    
14. Методика ознакомления детей с цифрами как знаками числа.
    
15. Методика обучения детей ориентировке во времени: формирование представлений о частях суток.
    
16. Методика ознакомления с календарным годом в старшем дошкольном возрасте.
    
17. Использование моделей и моделирования при формировании представлений о временных отношениях.
    

Литература


Тема № 1. История становления и развития методики математической подготовки дошкольников. Математическое развитие ребенка дошкольного возраста по методу Е.И.Тихеевой и Ф.Н.Блехер.

• Е.И.Щербакова: стр. 41 – 54
  
• А.А.Столяр: стр. 13 – 27
  

Тема № 2. Дидактические средства математического развития дошкольников. Требования к отбору и конструированию дидактических средств.

• А.А.Столяр: стр. 124 – 134
  
• Е.И.Щербакова: стр. 78 – 86
  
• Т.И.Ерофеева, Л.Н.Павлова, В.П.Новикова. Математика для дошкольников. – М., 1992, стр. 8-20
  

Тема № 3, 13, 14, 15. Понятие времени и ориентировки во времени. Особенности восприятия времени детьми разного возраста. Методика ознакомления дошкольников с временными отношениями.

• Рихтерман Т.Д. Формирование представлений о времени у детей дошкольного возраста. – М.,1991
  
• Локоть Н. Объемная модель: использование ее при формировании временных представлений. // Дошкольное воспитание 1991, № 1
  
• Щербакова Е., Фунтикова О. Формирование представлений и понятий о времени с помощью объемной модели.//Дошкольное воспитание 1986, № 7
  
• А.А.Столяр: стр. 259 – 276
  
• Е.И.Щербакова: стр. 140 – 142, 159 – 161, 189 – 193, 226 – 229
  
• В.В.Данилова: стр. 105 – 117
  
• Л.С.Метлина: стр. 30, 65 – 66,122 – 123, 200 – 201
  

Тема № 5, 6. Методика обучения дошкольников измерению объемов и массы тел.

• А.А.Столяр: стр.210 – 217, 224 – 230
  
• В.В.Данилова: стр. 70 – 77 (масса)
  
• Конспекты лекций
  

Тема № 8, 9. Методика ознакомления дошкольников с пространственными отношениями в разные возрастные периоды.

• А.А.Столяр: стр. 250 – 259
  
• Е.И.Щербакова: стр. 138 – 140, 157 – 158, 187 – 189, 219 – 225
  
• В.В.Данилова: стр. 100 – 104
  
• Л.С.Метлина: стр. 28 – 29, 63 – 65, 118 – 122, 197 – 200
  
• Мусейибова Т. Дидактические игры в системе обучения детей пространственным ориентировкам. //Дошкольное воспитание 1971, № 5
  
• Венгер Л.А. Игры и упражнения по развитию умственных способностей детей дошкольного возраста. – М., 1989
  

Тема № 8. Методика обучения дошкольников порядковому счету.

• А.А.Столяр: стр. 165
  
• В.В.Данилова: стр. 23 – 24
  
• Е.И.Щербакова: стр. 149 – 150
  
• Л.С.Метлина: стр. 106 – 107, 169 – 171
  

Тема № 11. Методика обучения счету с участием различных анализаторов.

• Л.С.Метлина: стр. 57 – 58, 101 – 102, 162
  
• Е.И.Щербакова: стр. 146 – 147, 164 – 167
  

Тема № 13. Методика ознакомления дошкольников с цифрами.

• А.А.Столяр: стр. 172 – 174
  
• Чуднова, Дошкольное воспитание 1991, № 8
  
• Белошистая, Дошкольное воспитание 2002, № 9
  
• Перепетайло, Дошкольное воспитание 2003, № 10,11
  

Содержание материалов в папке

1. Содержание самостоятельной работы студентов по курсу "Методика математического развития детей дошкольного возраста".
   
2. Литература.
   
3. Рекомендации к написанию контрольных работ по курсу «Методика математического развития детей дошкольного возраста».
   
4. Материалы лекции по теме «Роль математических знаний в умственном развитии детей дошкольного возраста».
   
5. Сравнительная таблица «Взгляды педагогов 17 – 19 веков на математическое развитие детей».
   
6. Фрагменты педагогических трудов. М.Морозова. Е.Тихеева. Счет в жизни маленьких детей. Ф.Н.Блехер. Математика в детском саду и нулевой группе.
   
7. Методические рекомендации по изучению темы «Дидактические средства математического развития дошкольников».
   
8. Материалы лекции по теме «Формирование у дошкольников представлений о массе и способах ее измерения».
   
9. Материалы лекции по теме «Методика работы по формированию представлений об объеме жидких и сыпучих веществ и способах его измерения с помощью условной меры».
   
10. Материалы лекции по теме «Развитие временных представлений у детей дошкольного возраста».
    
11. Материалы лекции по темам «Методика обучения порядковому счёту», «Изучение состава чисел из единиц и двух меньших».
    
12. Материалы лекции по теме «Обучение детей ориентировке в пространстве».
    
13. Материалы для изучения темы «Использование игр на пространственное моделирование в работе по формированию пространственных представлений».
    
14. Материалы для изучения темы «Логические блоки Дьенеша».
    
15. Материалы для изучения темы «Палочки Х.Кюизенера».
    
16. Материалы для изучения темы «Развивающие игры».
    
17. Материалы лекции по теме «Алгоритмы».
    

РОЛЬ МАТЕМАТИЧЕСКИХ ЗНАНИЙ

В УМСТВЕННОМ РАЗВИТИИ ДЕТЕЙ.


«Ум – хорошо организованная система знаний,

способность видеть мир в действенности и многообразии».

К.Д.Ушинский

Умственное развитие (УР) ребенка – важнейшая составная часть его общего психического развития. «Психическое развитие человека – это становление его деятельности, сознания и, конечно, всех обслуживающих их психических процессов» (В.В.Давыдов).

Следовательно, УР ребенка зависит от той деятельности, которую он выполняет в процессе обучения – репродуктивную или продуктивную.

Ядром УР является развитие умственных способностей ребенка, т.е. тех психологических качеств, которые определяют легкость и быстроту усвоения новых знаний и умений, возможность их применения для решения новых задач.

С понятием умственных способностей тесно связано понятие «математические способности» - это такие специфические особенности мыслительного процесса как

• Нешаблонность, неординарность
  
• Умение варьировать способы решения познавательных проблем
  
• Легкость перехода от одного пути решения к другому
  
• Умение выходить за пределы привычного способа деятельности и находить новые пути решения проблемы
  
• Умение проникать в сущность каждого изучаемого факта
  
• Умение видеть их взаимосвязи с др.фактами
  
• Выявлять специфические особенности в изучаемом материале
  
• Способность к формированию обобщенных способов действий, умение охватить проблему целиком, не упуская деталей.
  

Т.е. математическое мышление характеризуется гибкостью, глубиной и целенаправленностью.

Т.обр., приведенный анализ категории «математическое мышление» показывает, что она обусловлена:

1. наличием специальных знаний
   
2. развитием сенсорных способностей
   
3. развитием интеллектуальных способностей
   

УР как процесс и уровень включает в себя три компонента:


1. Накопление системы знаний и умений.


В д/в дети приобретают элементарные знания о множестве, числе, величинах, форме, временных и пространственных отношениях.

Важнейшую роль в развитии математических представлений играет обучение измерению как начальному способу познания количественной характеристике окружающего.

Одно из основных понятий математики – множество. Дети учатся устанавливать отношения между множествами (равенство, неравенство по количеству, независимость от пространственных характеристик, подчинение, пересечение, объединение, соподчинение и др.). На этой основе формируются понятия «число» и «натуральный ряд».

Дети знакомятся с рядом математических зависимостей:

- между количеством и числом

- между количественным и порядковым значением числа

- между компонентами измерительной деятельности

- между компонентами арифметических действий

- между количеством и величиной

- между количеством углов и названием геометрических фигур и др.


Особое внимание уделяется овладению практическими действиями: приложение, наложение, построение упорядоченных рядов, измерение, счет, вычисление, графические построения, умение пользоваться измерительными приборами, моделирование и др. При этом сами действия изменяются:

А) наложение – приложение – счет – вычисление

Б) счет с перекладыванием – счет с дотрагиванием – счет «глазами»

В) практическое сопоставление – сравнение «на глаз» - измерение условной меркой – измерение общепринятыми эталонами – установление зависимостей между единицами измерения – выполнение арифметических действий с именованными числами

Г) сенсорное обследование геом.фигур – анализ свойств геом.фигур – решение задач геом.характера – измерение периметра и площади


2. Освоение логических операций мышления, которые включаются в процесс овладения математическим содержанием.


Л.С.Выготский: «Научные понятия не усваиваются и не заучиваются ребенком, не берутся памятью, а возникают и складываются с помощью величайшего напряжения всей активности его собственной мысли».

Анализ и синтез – выделение элементов данного объекта, его признаков и свойств и соединение различных свойств в единое целое. В мыслительной деятельности человека они дополняют друг друга.

Способность к аналитико-синтетической деятельности предполагает не только умение выделять и соединять свойства, но и включать их в новые связи, видеть их новые функции. Например:

• Как по-разному назвать квадрат? Прямоугольник? Многоугольник?
  
• Что ты знаешь о числе «5»?
  
• Сколько треугольников в рисунке?
  

• Из каких геом. фигур составлена картинка?
  

• Каким арифметическим действие решается задача (обратная)?
  
• Подбери схему к условию задачи: «У Миши 5 марок. 3 марки он отдал Пете. Сколько марок осталось у Миши?». Предлагается переделать условие в соответствии со схемой.
  

3 ? ? 5

5 5 3 ?

3

• Игра «Когда это бывает?», «Что в мешочке?»
  

Сравнение – выделение признаков сходств и отличий между предметами. Например:

• Чем похожи и чем отличаются? Например, и , (5+3) и (3+5)?
  

?

1 и 7? 6 и 9?

• Что изменилось?
  

?

• Чего не хватает? 4 6 3 4 8 ? ?
  

5 5 4 ? ? 2 4

• Продолжи ряд.
  

• Что к чему подходит?
  

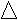
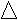
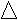
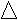
3 4 5

• Разложи по порядку. И др..
  

Классификация есть операция разбиения множества на классы с соблюдением определенных условий (множества не являются пустыми, не пересекаются, объединением является универсальное множество) на основе сравнения:

• По каким признакам можно разложить пуговицы в коробки?
  
• Найди место фигуре (игры с обручами)
  
• Разложи, что к чему подходит
  

В ходе этой работы дети должны научиться выполнять классификацию а) по предложенному основанию (разложи пуговицы по форме); б) самостоятельно выбирать основание (разложи пуговицы в коробочки так, чтобы в каждой коробочке лежали одинаковые); в) менять основание (как по-другому можно разложить пуговицы?).


Обобщение есть умение выделять существенные признаки математических объектов и объединять их в один класс.

Существует два типа обобщения:

А) эмпирическое, при этом обобщение является результатом индуктивных умозаключений (от частного к общему)

Б) теоретическое, при этом обобщение является результатом дедуктивных умозаключений (от общего к частному)

Необходимыми условиями формирования правильных обобщений являются:

А) рассматривание большого количества объектов, где повторяется свойство, закономерность

Б) варьирование несущественных признаков при постоянстве существенных.

Например, дети учатся обобщать группы предметов по количеству, геометрические фигуры, части суток, величины (дина – ширина), принцип образования числа, частные случаи, из которых выводятся свойства арифметических действий.


Абстрагирование – процесс выделения одних признаков при отвлечении от всех других, несущественных в данных условиях. На основании абстрагирования складывается представление о понятии.


3. Усвоение и расширение словарного запаса, совершенствование грамматического строя и связности речи.


Словарь: количественные наречия, числительные, прилагательные, глаголы, обозначающие способы действий, наречия, предлоги, существительные, названия свойств арифметических действий и др.

Грамматический строй: согласование в роде, числе, падеже («двумями руками», «первый, второй… (о матрешках), «к пять матрешек прибавить три матрешки», «карандашов», «один, два, три – всего два конфеток»).

Связная речь: доказательная речь, объяснение способа действия.


РАЗРАБОТКА ВОПРОСОВ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ ПРЕДСТАВЛЕНИЙ В ТРУДАХ ОТЕЧЕСТВЕННЫХ ПЕДАГОГОВ.


С начала 20 века в России начала создаваться научно-обоснованная дидактическая система обучения дошкольников математике. Ее начальный этап – начало 20 века – 40-е годы 20 века. В это время в дореволюционной России методические пособия адресовывались, как правило, одновременно семье и д/с, в них родители и воспитатели знакомились с содержанием обучения математике детей. В 1912 голу выходит пособие В.А.Кемниц «Математика в д/с»: игры, беседы, упражнения, изучение чисел 1-10, действий с ними, форм, величин, измерения, части и целого.

До 1939 года в д/с Ленинграда детей обучали счету по методике Л.В.Глаголевой, в которой она рекомендовала опираться на обе господствующие в то время теории: восприятия числа путем счета и путем образа. Она пропагандировала разнообразие методов:

• лабораторный (отработка практических действий с использованием наглядных материалов)
  
• исследовательский (поиск детьми ситуаций применения знаний, аналогичных изучаемым)
  
• иллюстративный (закрепление умений в продуктивной деятельности)
  
• наглядный
  
• игра.
  

Кр.того, Глаголева раскрыла приемы формирования представлений о величинах, измерении, делении целого на части.

Одним из ярких представителей в области просвещения была