Учебно-методическое пособие для проведения семинарских и практических занятий для студентов 1-го курса юридического факультета дневной формы обучения и отделения заочного обучения Составитель Половинкина Л. М

Вид материала

Учебно-методическое пособие

Содержание Тема 4. Учение об умозаключении Этот юноша – студент S остается неизменным, меняется связка и Р S. Цель обращения в том, чтобы отношение между понятиями, которое мыслится с точки зрения S Категорический силлогизм S). Больший термин в заключении является предикатом (Р Общие правила категорического силлогизма Правила фигур Правило 2-й фигуры Правило 3-й фигуры Правило 4-й фигуры Бег – вид легкой атлетики Лесть – ложь, т.к. извращает истину Логические задания Все истины – ценность Он не знает правил логики ЭВМ представляет собой сложное устройство

Подобный материал:

• Методические рекомендации (указания) для проведения занятий со студентами 3-го курса, 1188.37kb.
• Методические рекомендации (указания) для проведения занятий со студентами 1-го курса, 898.03kb.
• Методические рекомендации (указания) для проведения занятий со студентами 3-го курса, 1194.8kb.
• Программа и учебно-методические материалы по специальности 021100 юриспруденция, 327.61kb.
• Учебно-методическое пособие (для проведения семинарских занятий) для студентов заочной, 671.81kb.
• Кафедра истории, философии, социологии, политологии политология, 818.03kb.
• Программа и учебно-методические материалы по специальности 021100 юриспруденция Преподаватель:, 592.85kb.
• Учебно методический комплекс Для студентов специальности 1 24 01 02 Правоведение юридического, 1840.6kb.
• Методические рекомендации для проведения занятий со студентами 5-го курса юридического, 478.71kb.
• Методические рекомендации для проведения занятий со студентами 5-го курса юридического, 509.19kb.

Тема 4. Учение об умозаключении

Учебные вопросы:

1. Общее понятие об умозаключении.

2. Непосредственные умозаключения.

3. Опосредованные умозаключения: категорический силлогизм.

4. Сокращенные, сложные и сложносокращенные умозаключения.

5. Условно-категорический, разделительно-категорический и условно-разделительный силлогизмы.

1. Умозаключением называется форма мышления, посредством которой выводится новое суждение на основании одного или более известных суждений. Структура умозаключения: посылки, заключение, вывод. Исходные суждения, на основании которых получается новое, называется посылками. Новое суждение, полученное в результате сопоставления посылок, называется заключением. Логическая связь между посылками и заключением называется выводом.

Все студенты – будущие специалисты

Этот юноша – студент

Этот юноша будущий специалист.

Типы умозаключений: дедуктивные, индуктивные, по аналогии.

В отношении любых видов умозаключений задача логики состоит в установлении правильных способов выведения заключения из посылок. Заключение будет необходимо истинным, если правильность выведения его из посылок сочетается с истинностью последних. При нарушении этого условия заключение будет вероятностным (правдоподобным) или ложным.

Под дедуктивным умозаключением (лат. - выведение) понимают ход изложения материала в книге, лекции, уроке, докладе, беседе, споре, когда от общих суждений переходят к частным.

2. Дедуктивные умозаключения принято делить на непосредственные и опосредованные. Непосредственные умозаключения состоят из одной посылки, вывода и заключения. Заключение выводится с помощью логических операций превращения, обращения и противопоставления предикату.

Превращение – логическая операция умозаключения, при которой в заключении качество посылки изменяется на противоположное . S остается неизменным, меняется связка и Р на противоположное.

Превращению подлежат любые категорические суждения: А, Е, J, О.

1. А превращается в Е.
   

Схема превращения: Все S есть Р

Ни один S не есть не-Р.

2. Е превращается в А.
   

Схема: Ни один S не есть Р

Все S есть не-Р.

3. J превращается в О.
   

Схема: Некоторые S есть Р

Некоторые S не есть не - Р.

4. О превращается в J.
   

Схема: Некоторые S не есть Р

Некоторые S есть не - Р.

Как ни малосущественно это преобразование , оно все же раскрывает с новой стороны отношение S и Р: в посылке предмет обладает свойством, в заключении видно, что этот же предмет не может обладать свойством, противоречащим Р.

Обращение - логическая операция, при которой в заключении субъект и предикат меняются местами.

Обращение подчиняется правилу распределенности терминов в суждениях. В соответствии с этим различают простое (чистое) обращение и обращение с ограничением. Простым называется обращение без изменения количества суждения, если оба термина распределены или оба не распределены. Обращением с ограничением называется такое, при котором нераспределенный предикат меняется на нераспределенный субъект. Рассмотрим конкретнее.

1. А обращается в J с ограничением.
   

Схема: Все S есть Р

Некоторые Р есть S.

2. Е обращается в Е без ограничения.
   

Схема: Ни один S не есть Р

Ни один Р не есть S.

3. J обращается в I (Р и S не распр.).
   

Схема: Некоторые S есть Р

Некоторые Р есть S.

4. О, как правило, не обращается.
   

Теряется смысл.

Обращение – наиболее распространенный вид преобразования S. Цель обращения в том, чтобы отношение между понятиями, которое мыслится с точки зрения S, стало предметом мысли и с точки зрения Р. При этом логическое отношение между ними не меняется, а также и содержание мысли остается то же самое. Меняется только форма суждения.

Противопоставление предикату – логическая операция, при которой S в заключении становится противоположный предикат, а предикатом исходный субъект.

Противопоставление предикату – это результат операций превращения и обращения.

1. А становится Е.
   

Схема: Все S есть Р

Ни один не - Р не есть S.

2. Е становится J.
   

Ни один S не есть Р

Некоторые не-Р есть S.

3. J не противопоставляется.
   
4. О становится J.
   

Некоторые S не есть Р

Некоторые не -Р есть S.

Суть этой операции в том, чтобы показать, что каждое понятие может мыслиться не только в своем положительном содержании, но и по отношению к противоречащему ему понятию.

Таким образом, во множестве случаев правильно судить о смысле суждения возможно только после некоторого преобразования его формы. В результате этих операций устраняются все неясности и двусмысленности, порожденные недостаточно «прозрачной» грамматической формой, и устанавливается точное логическое отношение между S и Р.

3. Опосредованное умозаключение: категорический силлогизм (от греческого – выведение следствия).

Категорический силлогизм – вид опосредованного умозаключения, в котором из двух категорических суждений необходимо следует вывод.

Простой категорический силлогизм состоит из трех понятий (терминов):

меньшего, большего и среднего. Меньший термин в заключении является субъектом ( S). Больший термин в заключении является предикатом (Р). Они называются еще крайними и входят не только в заключение, но и в одну из посылок. Средний термин входит в обе посылки, но отсутствует в заключении. Обозначается латинской M. Он связывает меньший и больший термины. Поэтому категорический силлогизм определяют еще как умозаключение об отношении двух крайних терминов на основании их отношения к среднему.

Общие правила категорического силлогизма

1. Правила терминов
   

1. В силлогизме должно быть только три термина: S, М, Р.

Логическая ошибка основана на нарушении закона тождества и называется «учетверением терминов».

2. Средний термин должен быть распределен хотя бы в одной посылке

( см. таблицу распределенности терминов).

3. Термин, не распределенный в посылках, не может быть распределен в заключении.

Логическая ошибка, нарушающая это правило, называется «незаконным расширением большего или меньшего термина».

П. Правила посылок

1. Одна из посылок должна быть утвердительным суждением. Из двух отрицательных посылок нельзя вывести заключения.

2. Если одна из посылок – отрицательное суждение, то и заключение должно быть отрицательным.

3. Одна из посылок должна быть общим суждением. Из двух частных посылок нельзя вывести заключение.

4. Если одна из посылок – частное суждение, то и заключение должно быть частным.

По положению среднего термина М в посылках различают 4 фигуры силлогизма:


I фигура II фигура III фигура IV фигура

М Р Р М М Р Р М




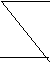
S М S М М S М S

Посылками в ПКС могут быть суждения всех 4-х видов: А, Е, J, О. Число возможных комбинаций видов в каждой фигуре получило название – «модусы фигур». Всего правильных модусов 19.

Правила фигур:

Правило 1-й фигуры: большая посылка – общая, меньшая – утвердительная. Согласно этому правилу, правильными являются четыре модуса: ААА, ЕАЕ, АJJ, ЕJО. Построение по 1-й фигуре имеет большую познавательную ценность, т.к. законы науки всегда формулировались в суждениях А.

Правило 2-й фигуры: большая посылка – общая, одна из посылок – отрицательная. Заключение – отрицательное. Правильными здесь являются модусы: ЕАЕ, АЕЕ, ЕJО, АОО. Отвергаются ложные подчинения, поэтому оправдательные юридические приговоры строятся по этой фигуре.

Правило 3-й фигуры: меньшая посылка – утвердительная, заключение – частное. В практике высказываний она применяется для доказательства исключений из правил. Модусы: ААJ, JАJ, АJJ, ЕАО, ОАО, ЕJО.

Правило 4-й фигуры: общеутвердительных заключений не дает. Если большая посылка - утвердительная, то меньшая посылка – общая, а если одна посылка – отрицательная, то большая посылка – общая. Построение по этой фигуре познавательной ценности не имеет, а применяется в практике обычной речи. Эта фигура была выделена Галеном через 500 лет после Аристотеля. Модусы: ААJ, АЕЕ, JАJ, ЕАО, ЕJО.

4. Категорический силлогизм состоит из двух посылок. Но в процессе рассуждений мы часто строим умозаключения в сокращенном виде, не высказывая всех трех частей. Умозаключение, в котором пропущена одна из его частей, называется сокращенным или энтимемой ( от греч. «в уме»).

Наиболее распространенной является энтимема с пропущенной большей посылкой, т.к. в ней обычно содержатся общеизвестные положения.

Я мыслю, следовательно, существую (Декарт).

Существовать, значит, быть воспринимаемым (Беркли).

При восстановлении энтимемы надо определить, какие части имеются. Заключение обычно стоит после слов : следовательно, поэтому, в результате этого... или перед словами: так как, потому что, ибо, ведь...

В процессе умозаключения мы выводим новое суждение. Развивая мысль, мы связываем ее с другими и строим новое умозаключение.

Умозаключение, в котором соединяются два простых силлогизма таким образом, что заключение одного становится посылкой другого, называется полисиллогизмом. Полисиллогизмы в рассуждениях обычно не высказываются в полной форме, а чаще всего сокращенно. Одной из разновидностей сложносокращенного силлогизма является сорит (с греч. «куча»). Он представляет собой как бы кучу посылок, из которых следует заключение. Сорит образуется путем отбрасывания промежуточных заключений, а следовательно, промежуточных большей (прогрессивный сорит) или меньшей (регрессивный сорит) посылок.

Все, укрепляющее здоровье, полезно

Спорт укрепляет здоровье

Легкая атлетика – спорт

Бег – вид легкой атлетики

Бег полезен.

Другой разновидностью сложносокращенного силлогизма является эпихейрема. Это полисиллогизм, в котором каждая из посылок является энтимемой.

Ложь вызывает недоверие, т.к. не соответствует истине

Лесть – ложь, т.к. извращает истину

Лесть вызывает недоверие.


5. Умозаключением, имеющим широкое распространение, является условно-категорический силлогизм. Он состоит из двух посылок: одна – импликативное суждение, другая – просто категорическое. Заключение – простое категорическое суждение.

Построение такого силлогизма подчиняется двум правилам:

1. Правило удаления импликации (УИ). Модус «утверждающий».
   

Схема: Если а, то в

а__

в

2. Правило «модус толленс» (от лат. «отрицающий»).
   

Схема: Если а, то в

не - в___

не - а

Но есть еще вероятностные модусы, которые не дают достоверного знания и не являются законом логики.

Схема первого: Схема второго:

Если а, то в если а, то в

в не - а__

вероятно а вероятно не - в

Люди, склонные иногда так рассуждать, в результате нередко из правильных посылок получают ложные заключения (демагогия).

Таким образом, для условно-категорического умозаключения является аксиомой следующее: Утверждение основания ведет к утверждению следствия, а отрицание следствия – к отрицанию основания.

Умозаключение, в котором одна из посылок является дизъюнктивным суждением, а другая – категорическим, называется разделительно-категорическим.

Имеет два правильных модуса:

1. Утверждающе-отрицающий
   

Схема:

Либо а, либо в либо а, либо в

а __ в_____

не–в не–а

Правило: в разделительной посылке дизъюнкция должна быть только строгой.

2. Отрицающе-утверждающий
   

Схема:

а или в а или в

не - а не - в__

в а

Правило: в разделительной посылке должны быть предусмотрены все возможные случаи (т.е. деление должно быть полным).

Условно-разделительным умозаключением называется такое, в котором одна из посылок является условным, а другая – дизъюнктивным суждением.

В зависимости от количества следствий в условной посылке различают дилеммы, трилеммы, полилеммы. Лемма – от греч. «предложение», отсюда дилемма – двойное предложение. В выводе такого умозаключения утверждается альтернатива, т.е. необходимость выбрать только одно из предложений.

Различают два вида дилемм: конструктивная (созидательная) и деструктивная (разрушительная).

Схема первой: Если а, то в, если с, то d

а или c________

в или d

Из двух оснований вытекают два различных следствия, из которых возможно только одно.

Схема второй: если а, то в, если с, то d

не - в или не - d______

не - а или не- с

Отличие в том, что во второй посылке указывается на ложность либо первого, либо второго следствия, а в заключении – ложность либо первого, либо второго основания.

Логические задания

1.Сделать заключение из посылки путем превращения, обращения и противопоставления предикату:

1. J Часто успех ослепляет нас.
   

Превращение: 1. Часто успех не является неослепляющим.

Обращение: 2. Часто ослепляющее нас есть успех.

Противопоставление

предикату: 3. Нет

2. Е Признание не унижает
   

Превращение: 1. Признание является неунижающим.

Обращение: 2. Ни одно унижение не признание.

Противопоставление

предикату: 3. Иногда неунизительное есть признание.


II. Доказать правильность категорического силлогизма:

Некоторые истины умозрительны

Все истины – ценность

Все ценности умозрительны.

Меньший термин – «ценности», больший термин – «умозрительны», средний термин – «истины».

Фигура – третья.

Модус – J АА.

1-й способ доказательства – третье правило терминов нарушается, четвертое правило посылок нарушается.

2-й способ доказательства – правило третьей фигуры нарушается.

3-й способ доказательства – среди правильных модусов третьей фигуры модуса JАА нет.

Следовательно, данный категорический силлогизм построен неправильно, заключение является ложным.

III. Восстановить энтимему до полного силлогизма и доказать его правильность.

1. Он не может найти ошибку, так как не знает правил логики.
   

Заключение – «он не может найти ошибку», меньшая посылка – «он не знает правил логики». Следовательно, пропущена и должна быть восстановлена большая посылка.

Все, знающие правила логики, могут найти ошибку

Он не знает правил логики

Он не может найти ошибку.

Энтимема восстановлена. Далее следует доказательство ( см. предыдущее упражнение).

2. «ЭВМ моделирует мыслительные процессы и представляет собой сложное устройство».
   

Большая посылка – «ЭВМ моделирует мыслительные процессы», меньшая посылка –«ЭВМ представляет собой сложное устройство».

Следовательно, пропущено и должно быть восстановлено заключение.

ЭВМ моделирует мыслительные процессы

ЭВМ представляет собой сложное устройство

То, что представляет собой сложное устройство, моделирует мыслитель- ные процессы.

Энтимема восстановлена. Далее следует доказательство.


IV.Оопределить схему, вид, модус и логическое значение сложных умозаключений табличным способом :

а в

1. Если ученик не хочет научиться, то учитель не сможет научить его.
   

а

Ученик хочет научиться.

в


Учитель сможет научить его.


Схема данного сложного силлогизма: а → в

а____

в (вероятно)

Вид – условно–категорический силлогизм.

Модус – вероятностный.

Формула данного силлогизма: ((а → в) а) → в

Далее по таблице логических значений определяется логическое значение данного силлогизма (см. тему «Суждение», задание Ш).