Учебно-методическое пособие для проведения семинарских и практических занятий для студентов 1-го курса юридического факультета дневной формы обучения и отделения заочного обучения Составитель Половинкина Л. М
| Вид материала | Учебно-методическое пособие |
- Методические рекомендации (указания) для проведения занятий со студентами 3-го курса, 1188.37kb.
- Методические рекомендации (указания) для проведения занятий со студентами 1-го курса, 898.03kb.
- Методические рекомендации (указания) для проведения занятий со студентами 3-го курса, 1194.8kb.
- Программа и учебно-методические материалы по специальности 021100 юриспруденция, 327.61kb.
- Учебно-методическое пособие (для проведения семинарских занятий) для студентов заочной, 671.81kb.
- Кафедра истории, философии, социологии, политологии политология, 818.03kb.
- Программа и учебно-методические материалы по специальности 021100 юриспруденция Преподаватель:, 592.85kb.
- Учебно методический комплекс Для студентов специальности 1 24 01 02 Правоведение юридического, 1840.6kb.
- Методические рекомендации для проведения занятий со студентами 5-го курса юридического, 478.71kb.
- Методические рекомендации для проведения занятий со студентами 5-го курса юридического, 509.19kb.
Тема 2 . Учение о понятии
Учебные вопросы:
1.Определение понятия.
2. Содержание и объем понятий.
3. Виды понятий.
4. Отношения между объемами понятий.
5. Обобщение и ограничение понятий.
1. Понятие – фундаментальная логическая форма, в которой предметы обобщаются по ряду признаков. Признаки бывают существенные и несущественные. В понятиях отражаются существенные признаки, т.е. необходимые для выделения предмета или класса предметов из остальных в рассматриваемом отношении. Признаки бывают отличительные и неотличительные. В понятиях отражаются отличительные, т.е. присущие только предметам, входящим в данный класс.
Таким образом, понятие – это форма мышления, в которой выражаются существенные и отличительные признаки предмета или класса предметов. Так, например, понятие «квадрат» образуется путем выделения таких существенных и отличительных признаков: «быть прямоугольной геометрической фигурой» и «иметь равные стороны».
Понятия образуются с помощью логических приемов сравнения, анализа, синтеза, абстрагирования, обобщения.
Сравнение – мысленное установление сходства или различия предметов по существенным или несущественным признакам.
Анализ – мысленное расчленение предметов на составные части, выделение в нем признаков.
Синтез – мысленное соединение признаков в единое целое.
Абстрагирование – мысленное выделение существенных признаков и отвлечение от несущественных.
Обобщение – мысленное объединение существенных и отличительных признаков предмета или класса предметов в понятие.
Понятия выражаются в словах или сочетаниях слов, которые имеют две важнейшие характеристики: значение и смысл. Значение (экстенсионал) термина – это имя, данное предмету. Смысл (интенсионал) – информация, которая связывается с ним. Понятие должно иметь определенные значения и смысл. В противном случае возникают логические ошибки, которые препятствуют пониманию.
Итак, понимать – знать значение и смысл термина, т.е. уметь мысленно выделять из рода предметов именно те, которые обладают данными видовыми отличительными признаками. 2. Всякое понятие имеет содержание и объем. Содержание - качественная сторона понятия, совокупность существенных и отличительных признаков предмета или класса предметов. Объем – количественная сторона понятия, класс обобщаемых в понятии предметов. Класс – множество предметов со сходными существенными признаками. Множество состоит из элементов, число которых может быть конечным или бесконечным. Так, содержание понятия «Солнечная система» - «группа планет (со спутниками), вращающихся по своим орбитам вокруг Солнца (звезды)», а объем – конечное множество, состоящее из 9 элементов. Содержание и объем понятия связаны законом обратного соотношения: чем шире объем понятия (т.е. больше количество обобщаемых в понятии предметов), тем уже его содержание (т.е. меньше признаков содержит оно), и наоборот, чем богаче содержание понятия, тем уже его объем. Например: «Литературное произведение» - «роман» - «роман Л.Н. Толстого «Война и мир». Объем сужается до одного элемента, содержательные характеристики становятся богаче и разнообразнее. Различение содержания и объема понятия, уяснение их соотношения необходимо для многих логических операций, а именно определения понятия, обнаружения его видовых характеристик, обобщения и ограничения, деления понятия.
3. Понятия по объему делятся на единичные и общие. Объем единичного понятия составляет один элемент. Например: «столица современной России», «древнегреческий философ, отравленный по приговору суда ядом цикуты» и т.д. Объем общего понятия включает множество элементов: «спортсмен, победивший в Олимпийских играх», «государство», «человек, умеющий играть на скрипке».
Можно выделить особую группу понятий, так называемые «пустые» понятия, объем которых представляет пустое множество, т.е. не содержит ни одного элемента. Одни из них образуются в результате заблуждений, свойственных развитию научного познания ( «теплород», «флогистон», «вечный двигатель»), другие в результате логического противоречия («человек, знающий все европейские языки, но не знающий болгарского языка»), третьи создаются фантазией человека («человек, побывавший на Марсе», «Дед Мороз» и т.д.).
По содержанию понятия различаются на конкретные и абстрактные. В конкретных мыслятся отдельные предметы или классы предметов с определенными признаками: «психолог Леонтьев», «черный», «искренний человек». Абстрактными называются понятия, в которых мыслится общий признак, взятый отдельно от предмета, или отношение между предметами: «белизна», «твердость», «глухота», «тождество» и т.д.
Понятия бывают относительные и безотносительные. Относительными (или соотносительными) называются понятия, существование одного из которых предполагает наличие противоположного: «родители – дети», «начальник – подчиненный», «раб – рабовладелец» и т.д. Они образованы за счет использования двухместного отношения. В безотносительных понятиях предметы мыслятся существующими самостоятельно: «человек», «дом», «город», «планета»...
В зависимости от наличия или отсутствия признака (отношения) понятия делятся на положительные и отрицательные. Положительные понятия употребляются без частиц «не», «без», «а» (кроме тех, которые без них не употребляются): «говорящий по-английски», «далекая звезда», «хороший поступок», «ненависть», «беспечность».... Отрицательные понятия означают отсутствие качества: «некрасивое лицо», «бескорыстная помощь», «алогичный вывод»...
По типу обобщаемых предметов понятия делятся на собирательные и несобирательные. Собирательными называются понятия, в которых группа однородных предметов мыслится как единое целое. Причем содержание такого понятия нельзя отнести к каждому элементу отдельно. Такими понятиями являются «стадо», «библиотека», «толпа», «созвездие Большая Медведица». Несобирательные понятия – это такие, содержание которых можно отнести к отдельному предмету множества: «игрушка», «студент», «река», «автомобиль» и т.д.
Логическое задание
Дать логическую характеристику понятиям:
Родина – общее, конкретное, относительное, положительное, несобирательное.
Сестра – общее, конкретное, относительное, положительное, несобирательное.
Безнравственность – общее, абстрактное, безотносительное, отрицательное, несобирательное .
Лес – общее, конкретное, безотносительное, положительное, собирательное.
4. Понятия не могут вступать ни в какие отношения, если принадлежат к разным родам. Такие понятия называются несравнимыми. Сравнимые понятия принадлежат к одному роду. Сравнимые понятия делятся на совместимые и несовместимые. Совместимыми называются понятия, объемы которых полностью или частично совпадают. Несовместимыми – объемы которых не совпадают ни в одном элементе. Существует три типа совместимости – равнозначность, перекрещивание, подчинение и три типа несовместимости: соподчинение, противоположность, противоречие.
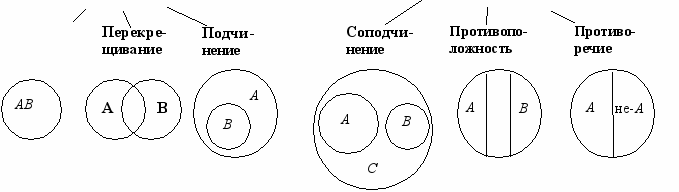
Отношение между объемами понятий изображают с помощью круговых схем, получивших название «кругов Эйлера». Математик и логик Эйлер (ХVIII в.) первый предложил обозначать объем понятия кругом.
Приведем таблицу логических отношений между объемами понятий и объясним типы отношений.
Сравнимые понятия
 Совместимые Несовместимые
Совместимые НесовместимыеРавно-
значность
Равнозначными называются понятия, которые различаются по своему содержанию, но совпадают по объему. Например: А – равносторонний прямоугольник; В – квадрат.
Перекрещивание – отношение между понятиями, объемы которых частично совпадают, т. е. они имеют общие элементы. Например: А – студент; В – отличник.
Подчинение (субординация) характеризуется тем, что объем одного понятия (подчиненного) целиком входит объем другого (подчиняющего), но не исчерпывает его. Например: А – юрист; В – адвокат.
Соподчинение (координация) – это логическое отношение между объемами понятий, не совпадающими друг с другом. Это разные виды одного рода.
Например: А – комета; В – звезда; С – планета во множестве небесных тел.
Противоположность (контрарность) – это логическое отношение между объемами двух понятий, которые являются видами одного рода, при этом одно из них содержит какие-либо признаки, а другое – исключает их и заменяет на противоположные. Например: А – храбрость; В – трусость.
Противоречие (контрадикторность) – характеризует отношение между объемами двух понятий, одно из которых указывает на некоторые признаки, а другое – их отрицает, но не заменяет другими. Употребляется оно с отрицательными частицами «не», «без» и т.д. Например: А – честный человек; В – нечестный человек.
Логическое задание
1. Определить отношения между понятиями и отразить в кругах Эйлера:
1

.1. А – преступление; В – терроризм;
С – спекуляция;
Д – хищение.
1.2. А – законченная повесть; В – незаконченная повесть;
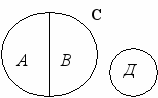
С – повесть; Д – рассказ.
1
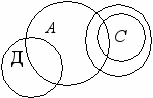 .3. А– орудие преступника; В – огнестрельное оружие; С – боевой пистолет;
.3. А– орудие преступника; В – огнестрельное оружие; С – боевой пистолет;Д – нож.
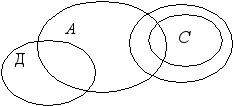
1.4. А – человек; В – карлик; С – великан; Д – европеец.

5. Обобщение и ограничение понятий – это операции, уточняющие содержание понятия и его объем. Они осуществляются на основе закона обратного соотношения содержания и объема понятия.
Обобщение – это логический переход от понятия с меньшим объемом (видового) к понятию с большим объемом (родовому) путем отбрасывания видовых содержательных признаков. Предел обобщения – общенаучное понятие или философская категория. Например: Кошка – млекопитающее – позвоночное – организм – материя.
Расширяя объем понятия путем отбрасывания содержательных характеристик, мы переходим к универсальному понятию, включающему в себя огромное множество элементов, но с предельно абстрактным содержанием. Например: Партия – массовая политическая организация – политическая организация – организация.
Кислота – сложное химическое вещество – химическое вещество – вещество –материя.
Ошибки обобщения:
- «Скачок в обобщении» – нарушение последовательности обобщения, когда пропускается промежуточный род. Например: пальто – одежда.
- Попытка обобщить категорию (переход от рода к виду). Например: материя – космос.
Ограничение – логический переход от понятия с большим объемом (родового) к понятию с меньшим объемом (видовому) путем введения видовых содержательных признаков. Предел ограничения – единичное понятие. Например: Кислота – неорганическая кислота – бескислородная неорганическая кислота – хлорная кислота (НСl).
Здание – административное здание – нижегородское административное здание – здание городской думы.
Предложение – простое предложение – односоставное простое предложение – односоставное личное простое предложение «Люблю грозу в начале мая».
Сужая объем понятия путем введения содержательных характеристик, мы переходим к единичному понятию, объем которого составляет один элемент, а содержательные характеристики многообразны.
Ошибки ограничения:
- «Скачок в ограничении» – нарушение последовательности ограничения, когда пропускается промежуточный вид.
- Попытка ограничить единичное понятие (переход от вида к роду).
- Подмена операции ограничения делением на части. Например: «Здание – окно» или «город - центр города» - ложное ограничение, т.к. нарушено логическое отношение подчинения. «Всякое окно есть здание» или «всякий центр города есть город» - это алогичные утверждения.
Умение анализировать понятия, овладение логическими операциями с характеристиками понятий способствует развитию абстрактного мышления, приучает к ясности, последовательности рассуждения.
Логическое задание
Обобщить и ограничить понятие:
Районный центр
(обобщение) (ограничение)
1. Центр 1. Районный центр РФ
2. Населенный пункт 2. Районный центр РФ
Волго-Вятского региона
3. Пункт 3. Районный центр РФ
Волго-Вятского региона Нижегородской области
4. Пространство 4. г. Бор
Тема 3. Учение о суждении
Учебные вопросы:
1. Определение суждения.
2. Типы простого суждения.
3. Категорические суждения и их классификация.
4. Распределенность терминов в суждениях.
5. Логические отношения между простыми суждениями («Логический квадрат»).
6. Определение сложного суждения.
7. Виды сложного суждения.
8.Таблица логических значений сложного суждения.
1. Суждение – форма мышления, в которой что-либо утверждается или отрицается о существовании предметов, их связях, свойствах или отношениях.
«Москва многочисленнее Нижнего Новгорода».
«Некоторые грибы – ядовиты». «Не существует беспричинных явлений».
Суждение имеет два логических значения. Оно может быть истинным или ложным. Если то, что утверждается или отрицается в суждении, соответствует действительности, то суждение является истинным. В противном случае - суждение ложно.
Мысль, выраженная в форме суждения, имеет свою структуру:
Термины суждения:
а) субъект ( S) - понятие о предмете суждения;
б) предикат ( Р ) – понятие о связях, свойствах или отношениях, которыми обладает или не обладает предмет суждения;
в) связка – способ соединения предмета мысли и его признаков. Указывает на наличие или отсутствие признаков. Выражается одним словом (есть, суть, является, бывает, не есть, не суть, не является, не бывает) или группой слов, или тире, или простым согласованием слов.
Суждения выражаются в предложениях, но не все предложения содержат в себе суждение. Вопросительные предложения не содержат в своем составе суждение. В них ничего не отрицается и не утверждается, значит, их нельзя определить в терминах истины и лжи. По этой же причине и побудительные предложения, которые только побуждают к действию, не содержат суждения, не являются суждениями.
Итак, только повествовательные предложения содержат мысль в форме суждения. Есть еще один признак не–суждения: это предложения, в которых высказываются о личных вкусах и чувствах и которые не могут быть определены как истинные или ложные. Например: «Я желаю...» или «Мне нравится...», «Я верю...».
Суждение как способ логической связи между понятиями, состоящее из одного предложения, называется простым.
2. Простые суждения бывают трех типов: атрибутивные (атрибут – признак, свойство), суждения с отношениями и суждения существования.
Атрибутивные, или категорические, - суждения, в которых утверждается или отрицается принадлежность предмету известных свойств, состояний, видов деятельности. Например: «У розы – приятный запах», «Все дельфины – млекопитающие», «Терьер – это порода собак». В каждом атрибутивном суждении есть предмет мысли (S), предикат (Р) и связка.
Суждения с отношениями – такие, в которых высказывается об отношениях между предметами. Их формула «а R в», где пропозиционные переменные:
а и в - имена предметов,
R - отношение между ними. Например: «Отцы старше детей», «Эльбрус выше Монблана», «Гоголь родился позднее Грибоедова».
В суждениях существования утверждается или отрицается наличие предметов в действительности. В них употребляются слова «есть» или «нет», «существует» или «не существует». Например: «Без борьбы мнений нет движения к истине», «В России существует кризис», «У всякого безумия есть своя логика».
Особое место в классификации простых суждений занимают выделяющие и исключающие суждения.
Выделяющими называются суждения, в которых утверждается или отрицается принадлежность признака только к данному классу предметов. В них употребляются слова «только», «лишь». Например: «Только заслуга достойна награды», «Лишь богач да глупец делают то, что хотят».
В исключающих суждениях говорится о принадлежности или отсутствии признака у всех предметов класса, кроме некоторой части. Их можно узнать по словам «за исключением», «кроме», «помимо», «не считая»... Например: «Никто, кроме мужественного, не заслуживает уважения».
3. Более подробно рассмотрим атрибутивные суждения, ибо в них представлены все части простого суждения, и они являются наиболее распространенным типом суждения.
Атрибутивные суждения называются также категорическими (греч. – ясный). Они делятся по двум признакам: по качеству и количеству.
Качество суждения выражается связкой. Она может быть утвердительной («есть», «бывает», суть») в том случае, если признак у предмета присутствует, или отрицательной («не есть», «не бывает», «не суть»), если признак отсутствует. Например: «Некоторые студенты занимаются научной работой», «Ни один карась не является хищной рыбой».
Количество суждения выражается квантором. Суждение может быть общим, если употребляется квантор общности, и частным, если используется квантор существования. Например: «Все люди смертны», «Некоторые грибы не являются съедобными».
В формальной логике принята объединяющая классификация суждений по качеству и количеству. Выделяются 4 вида категорических суждений:
- Общеутвердительные (А)
Все S есть Р.
Все цветы – растения.
- Общеотрицательные ( Е )
Ни одно S не есть Р.
Ни один кит не является рыбой.
- Частноутвердительные ( J )
Некоторые S есть Р
Некоторые студенты – спортсмены.
- Частноотрицательные ( О ).
Некоторые S не есть Р.
Некоторые птицы не являются водоплавающими.
4. Для логического анализа суждений необходимо определить отношения между объемами терминов суждения – субъекта и предиката. Иными словами, установить – распределены они или нет.
Термин считается распределенным, если его объем полностью включен или исключен из объема другого термина.
Термин считается нераспределенным, если его объем лишь частично включен или исключен из объема другого термина. Так, в общеутвердительных суждениях (А), объем S полностью включен в объем Р, а объем Р лишь частично –в объем S. Следовательно, S распределен, а Р нераспределен.
Чтение – лучшее учение.
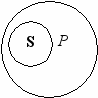
S – чтение
Р – лучшее учение
В общеотрицательных суждениях ( Е ) объем S полностью исключен из объема Р, и наоборот. Следовательно, S и Р являются распределенными.


Н
S
Р
и один герой не является трусом.S – герой
Р – трус
В
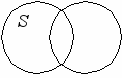 частноутвердительных суждениях ( J), объем субъекта частично включается в объем предиката, а объем предиката – частично включается в объем субъекта. Следовательно S и Р нераспределены.
частноутвердительных суждениях ( J), объем субъекта частично включается в объем предиката, а объем предиката – частично включается в объем субъекта. Следовательно S и Р нераспределены.Не все студенты пришли на лекцию.
S
Р
– студентыР – пришли на лекцию
Наконец, в частноотрицательных суждениях ( О) объем субъекта частично исключен из объема предиката, а объем предиката – полностью исключен из объема субъекта. Следовательно, S нераспределен, а Р распределен.
Некоторые студенты не пришли на лекцию.
S




– студенты
Р
 – пришли на лекцию
– пришли на лекциюДля установления распределенности используется таблица распределенности терминов в простом суждении.
| | А | Е | J | О |
| S | + | + | _ | _ |
| Р | _ | + | _ | + |
+ термин распределен;
- термин нераспределен.
5. Для анализа простого суждения надо знать те отношения, которые логически допустимы между простыми суждениями. Простые суждения могут быть несравнимы, а значит, не вступать ни в какие отношения в том случае, если у них различные субъекты или предикаты. Если же они различаются только по связке (утвердительной или отрицательной) или по квантору, то они являются сравнимыми, их можно поставить в логическую зависимость и определить их логическое значение (истинны они или ложны).
Эти отношения принято изображать в виде схемы, которая в логике получила название «Логический квадрат». Вершины квадрата обозначают виды простых суждений, а его стороны и диагонали – логически допустимые отношения между ними.




А
J
Е
О
контрарность
субконтра
субконтрарность
Для установления логических значений простых суждений необходимо знать правила, которым подчиняются эти отношения.
Правила подчинения: (между А и J, а также Е и О).
Если А и Е истинны, то J и О истинны.
Если А и Е ложны, то J и О неопределенны (истинны или ложны).
Если J и О истинны, то А и Е неопределенны ( истинны или ложны).
Если J и О ложны, то А и Е ложны.
Правила контрарности (противоположности)
(между А и Е):
Если одно из них истинно, то другое ложно.
Если одно из них ложно, то другое неопределенно ( истинно или ложно).
Правила субконтрарности (частичной противоположности) (между J и О):
Если одно из них ложно, то другое истинно.
Если одно из них истинно, то другое неопределенно (истинно или ложно).
Правила контрадикторности (противоречия) (между А и О; Е и J)
Если одно из них истинно, то другое ложно.
Если одно из них ложно, то другое истинно.
Знание правил «Логического квадрата» необходимо при сопоставлении различных сравнимых суждений для анализа их способности выражать истину.
6. Сложные суждения образуются путем соединения между собой простых при помощи логических союзов.
Простые суждения в составе сложного обозначаются пропозиционными переменными: а, в, с, d, е...
Если соединяются больше двух простых суждений, то в этой сложной логической конструкции различают главный и подчиненные логические союзы.
7. Вид сложного логического суждения определяется по главному союзу. Сложные суждения бывают трех видов:
- Соединительные (или конъюнктивные) (а
 в)
в)
«Счастье обманет и в лес уйдет».
- Разделительные (или дизъюнктивные):
 2.1. нестрогая дизъюнкция (а
2.1. нестрогая дизъюнкция (а  в)
в)«Или слушаю преподавателя, или смотрю в окно».
2.2. строгая дизъюнкция (а
 в)
в)«Либо пан, либо пропал».
- Условные ( или импликативные)
3.1. простая импликация (а→ в)
«Если стоит туман, то аэропорт закрыт».
3.2. двойная импликация (а ↔ в)
«Наше мышление только тогда логически правильно, когда мы связываем в мыслях то, что связано в самой действительности».
8. Логическое значение сложного суждения зависит от логических значений простых, входящих в него. Для его определения пользуются таблицей логических значений сложных суждений. Чтобы построить таблицу, надо знать:
- число строк в таблице;
- интервал смены логических значений истины и лжи;
- правила всех видов сложных суждений.
Число строк в таблице (С) зависит от количества простых суждений в сложном (n) и определяется по формуле: С = 2n. Так, например, для сложного суждения, состоящего из
 2-х простых (а, в), С = 22 = 4.
2-х простых (а, в), С = 22 = 4.Интервал смены логических значений истины и лжи для а = 4 : 2 = 2 (и, и; л, л), а для в = 2 : 2 = 1 (и, л; и, л) .
Примечание: Если простые суждения, входящие в сложные, являются отрицательными (
 ,
, 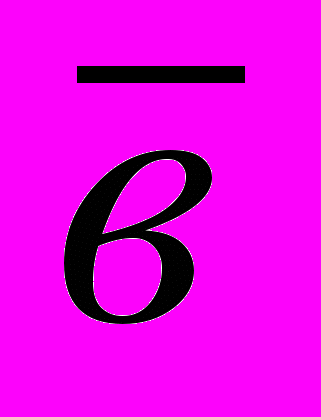 ,
, 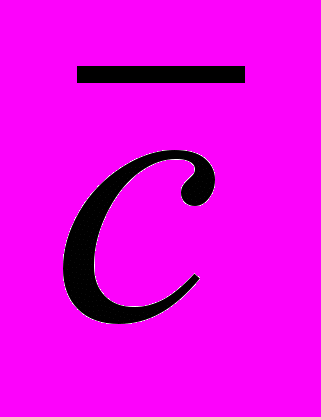 ,
,  ,
, 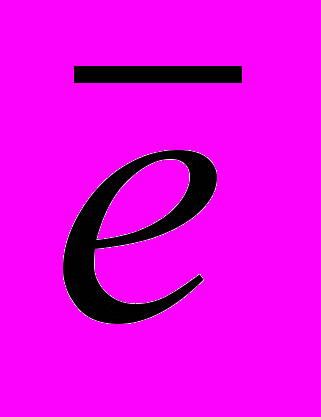 ), то их логические значения в таблице меняются на противоположные.
), то их логические значения в таблице меняются на противоположные.Таблица логических значений сложных суждений
| а | в | а  в в | а  в в | а  в в | а→в | а↔ в |     | 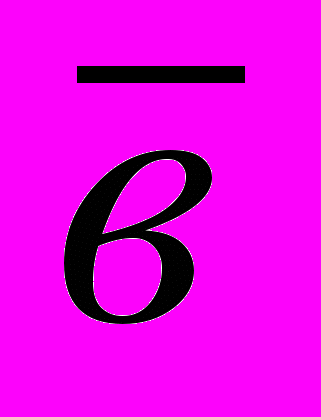 |
| и | и |  и | и |  л л | и  |  и | л | л |
| и | л | л | и | и | л | л | л | и |
| л | и | л | и  | и  | и | л  | и | л |
| л | л | л | л | л | и | и | и | и |

Для того чтобы проверить логическое значение сложного суждения, надо:
 1. Определить количество простых суждений в сложном.
1. Определить количество простых суждений в сложном. 2. Обратить внимание на то, утвердительные или отрицательные эти простые суждения.
2. Обратить внимание на то, утвердительные или отрицательные эти простые суждения. 3. Выделить типы логических связей между частями сложного суждения (по логическим союзам), различить главный и подчиненный типы связей, если простых суждений больше двух.
3. Выделить типы логических связей между частями сложного суждения (по логическим союзам), различить главный и подчиненный типы связей, если простых суждений больше двух. 4. Составить формулу сложного суждения, заключить подчиненные части в скобки.
4. Составить формулу сложного суждения, заключить подчиненные части в скобки. 5. Проверить логическое значение формулы табличным способом.
5. Проверить логическое значение формулы табличным способом.Логические задания
I. Определить термины, вид, распределенность терминов простого суждения:
- Всякое слово имеет смысл.
Субъект – «слово»; предикат – «имеет смысл»; квантор общности – «всякое».
Вид суждения – общеутвердительное (А).
По таблице распределенности терминов субъект данного простого суждения распределен, предикат не распределен.
- Никакое знание не является бесполезным.
Субъект – «знание»; предикат – «бесполезным»; связка – «не является»; квантор общности – «никакое».
Вид суждения – общеотрицательное (Е).
По таблице распределенности терминов субъект и предикат распределены.
П. Определить отношения по логическому квадрату между простыми суждениями:
- Не всякую истину полезно изрекать.
Данное суждение вида J вступает в отношения подчинения с суждением вида А, субконтрарности с суждением вида О, контрадикторности с суждением вида Е. При условии его истинности суждение вида А – Всякую истину полезно изрекать – неопределенно, вида О – Некоторые истины не полезно изрекать – неопределенно, суждение вида Е – Ни одну истину не полезно изрекать – ложно. При условии его ложности суждение вида А – ложно, вида О – истинно, вида Е – истинно.
- Некоторые страны Европы не являются демократическими.
Данное суждение вида О вступает в отношения подчинения с суждением вида Е, субконтрарности с суждением вида J, контрадикторности с суждением вида А. При условии его истинности суждение вида Е – Ни одна страна Европы не является демократической – неопределенно, суждение вида J –Некоторые страны Европы являются демократическими – неопределенно, суждение вида А –Все страны Европы являются демократическими – ложно. При условии его ложности суждение Е – ложно,
J - истинно, А – истинно.
Ш. Записать в виде формулы, определить вид и логическое значение табличным способом следующих сложных суждений:
- «Если наши дети – это наша старость, то правильное воспитание – это наша счастливая старость, плохое воспитание – наше горе...» (А.С. Макаренко).
Сложное суждение состоит из трех простых суждений (переменных), обозначенных а, в, с. Их соединяют логические союзы – импликация и конъюнкция.
Формула сложного суждения: ( а → (в с))
Вид суждения – импликативное суждение.
По таблице логических значений определяется логическое значение данного сложного суждения.
| а | в | с | в с | а → ( в с) |
| и | и | и | и | и |
| и | и | л | л | л |
| и | л | и | л | л |
| и | л | л | л | л |
| л | и | и | и | и |
| л | и | л | л | и |
| л | л | и | л | и |
| л | л | л | л | и |
Из таблицы видно, что формула для 5 наборов логических значений истинна,
а для 3 ложна. Общий вывод: данное сложное суждение не является тождественно-истинным, т.к. в последней колонке есть ложь.
2) «Детская душа в одинаковой мере чувствительна и к родному слову, и к красоте природы, и к музыкальной мелодии» ( В.А. Сухомлинский).
Данное сложное суждение состоит из трех простых суждений (переменных), обозначенных а, в, с. Все три простых суждения соединены логическим союзом – конъюнкцией.
Формула сложного суждения: ( (а в) с ).
Вид суждения – конъюнктивное суждение.
По таблице логических значений определяется логическое значение данного сложного суждения.
| а | в | с | (в с) | (а в) с) |
| и | и | и | и | и |
| и | и | л | л | л |
| и | л | и | л | л |
| и | л | л | л | л |
| л | и | и | и | и |
| л | и | л | л | и |
| л | л | и | л | и |
| л | л | л | л | и |
Из таблицы видно, что формула для 1–го набора логических значений истинна, а для остальных – ложна. Общий вывод: данное сложное суждение не является тождественно-истинным, т.к. в последней колонке есть ложь.
