Тема урока: Повторение материала по теме «Основы логики»
| Вид материала | Урок |
- План-конспект открытого урока в 5 «В» классе по теме «Семья», 43.36kb.
- Программы: Основы логики и логические основы компьютера. Тип урока: урок объяснения, 129.96kb.
- Тема урока Дата, 270.26kb.
- Тема урока: «Математические модели», 126.97kb.
- Тема урока: Реальные кристаллы. Аморфные тела, 50.1kb.
- Урок по теме «Основы логики и логические основы компьютера», 276.49kb.
- План урока: Организационный момент Повторение изученного по теме Объяснение нового, 82.52kb.
- Тема урока: Операции логики высказываний. Таблицы истинности, 207.3kb.
- Конспект урока русского языка по теме: «Повторение изученного в 5 классе о глаголе», 101.93kb.
- Тема урока : «Базовые логические элементы», 87.8kb.
- 6-8 верных ответов – «3»;
- 9-10 верных ответов – «4»;
- 11-12 верных ответов – «5»
2. Логические законы
«Мы должны быть рабами законов, чтобы стать свободными»
Цицерон (Рим, II – I вв. до н.э.)
Внимание на экран. (Демонстрируется слайд)
«Найди пару» Провести соответствие между законом и названием (указать соответствующий номер названия закона)
| Закон | № закона | | № закона | Название закона |
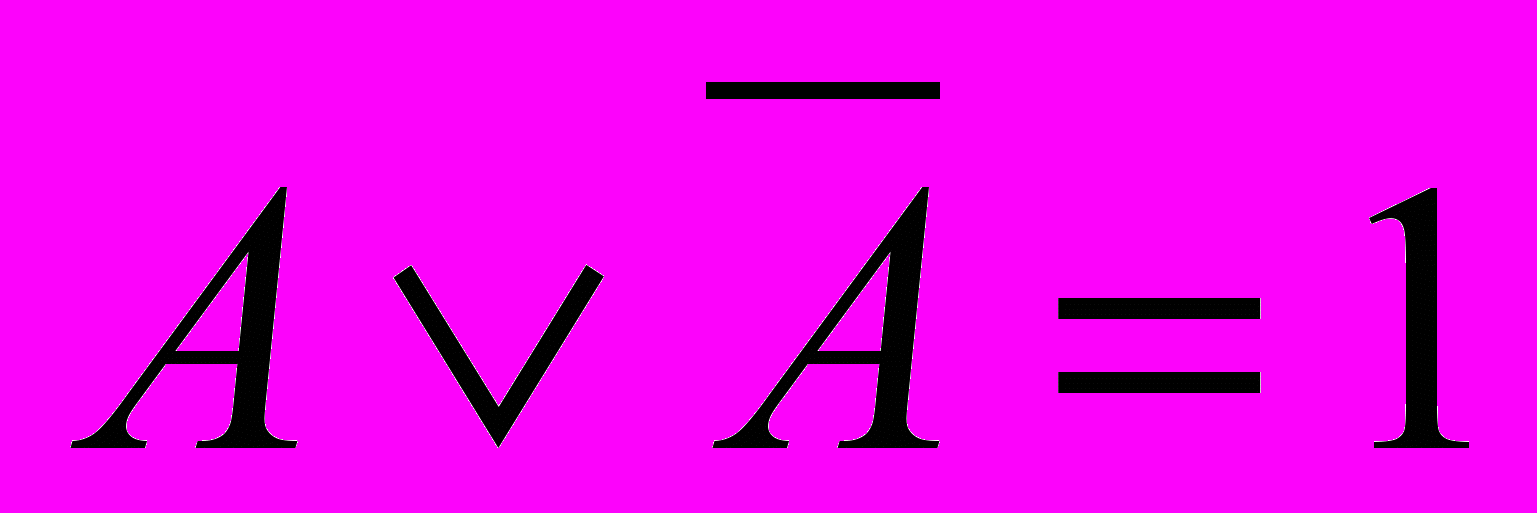 | | | | Закон де Моргана |
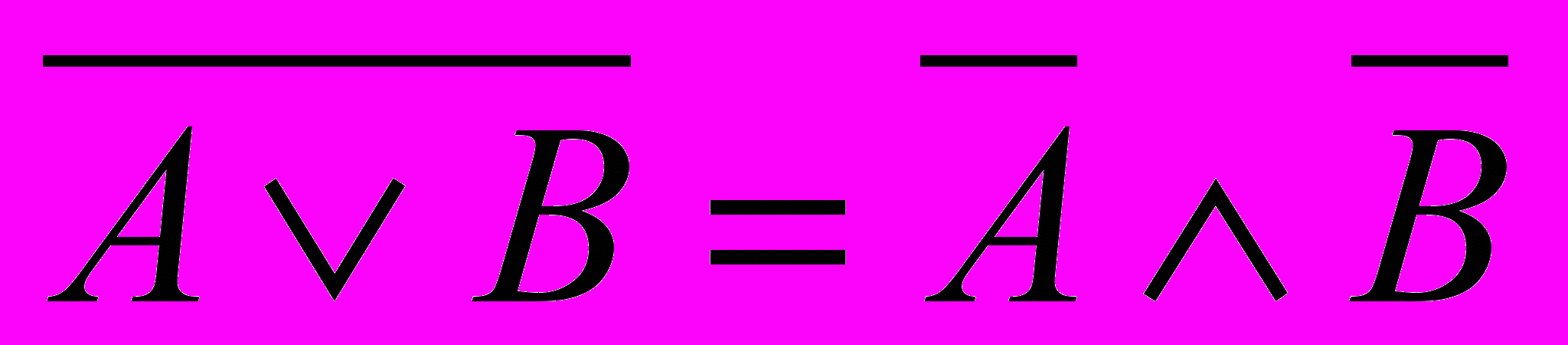 | | | | Закон двойного отрицания |
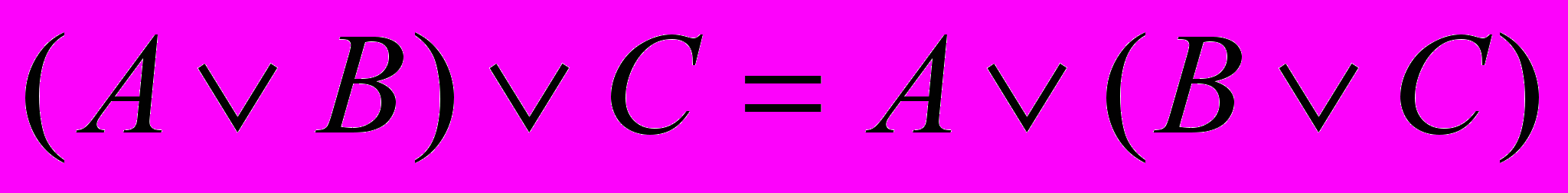 | | | | Закон коммутативности |
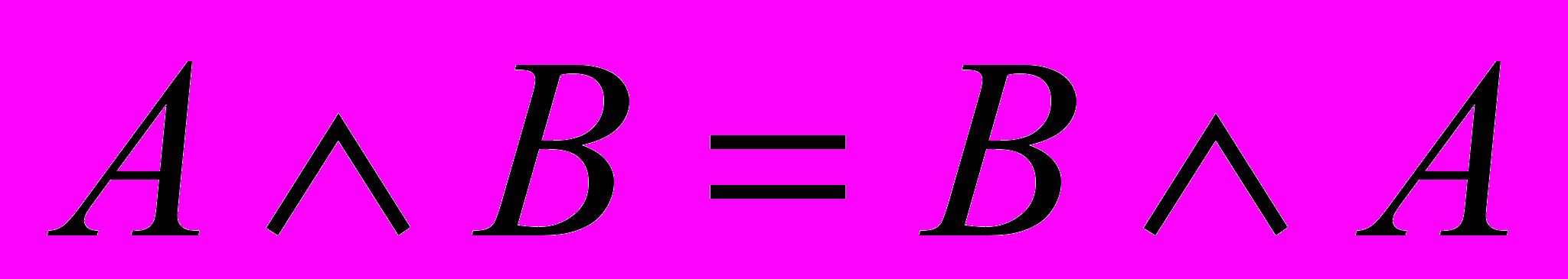 | | | | Закон ассоциативности |
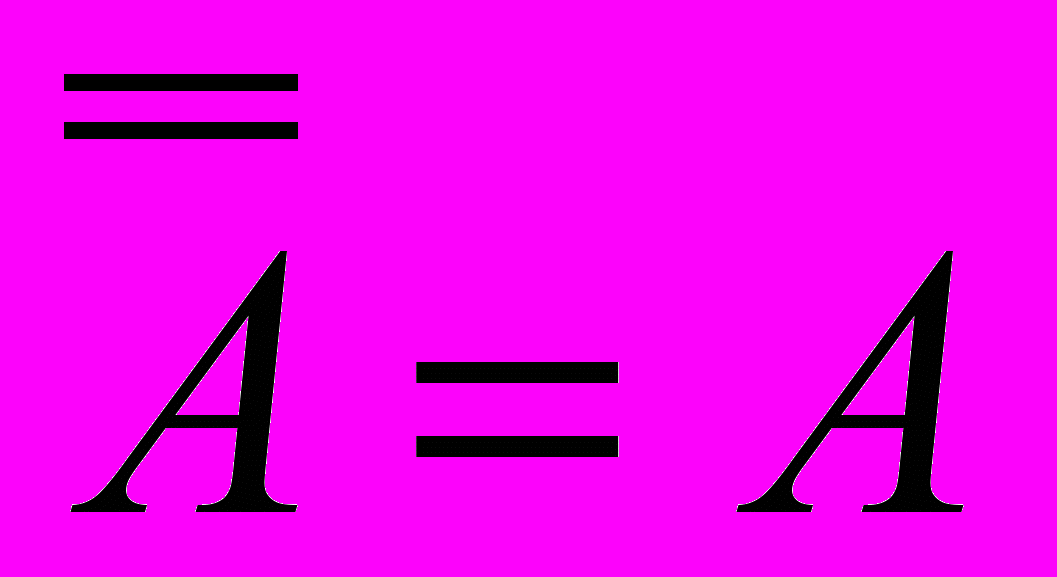 | | | | Закон дистрибутивности |
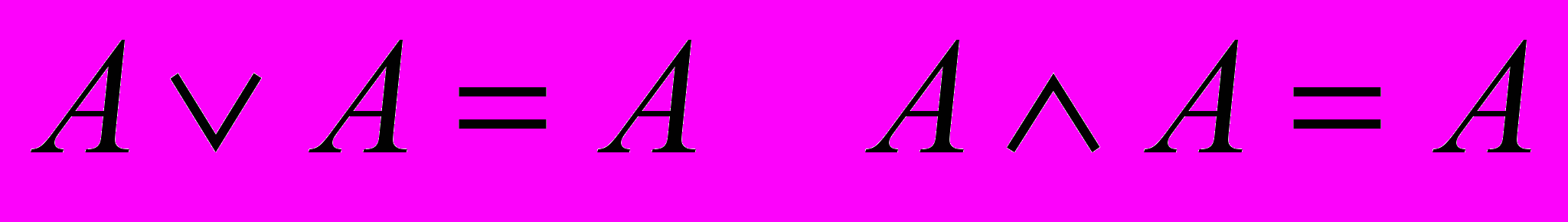 | | | | Закон исключения констант |
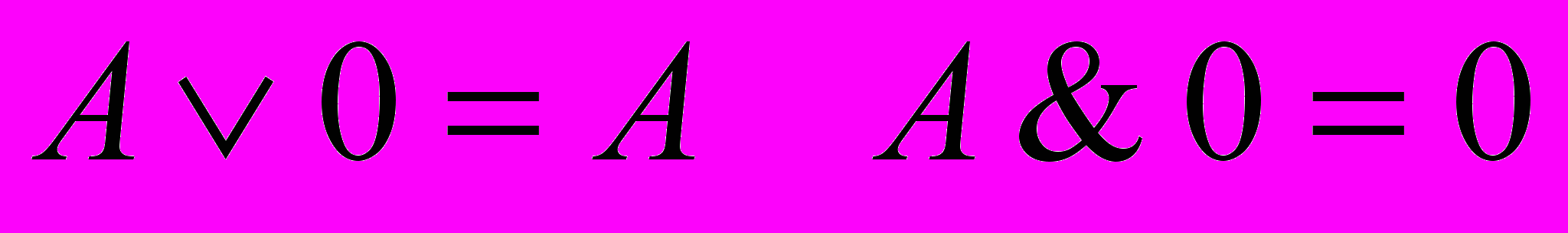 | | | | Закон равносильности |
 | | | | Закон непротиворечия |
 | | | | Закон исключенного третьего |
- 8-9 верных ответов – «5»;
- 7-6 верных ответов – «4»;
- 4-5 верных ответов – «3».
3. «Подбери верное»
Укажите обозначение логических операций соответствующих таблицам истинности
-
А
В
0
0
0
0
1
0
1
0
0
1
1
1
А
В
0
0
0
0
1
1
1
0
1
1
1
1
А
В
0
0
1
0
1
1
1
0
0
1
1
1
А
В
0
0
0
0
1
0
1
0
0
1
1
1
А
0
1
1
0
А и В
А или В
А =>B
AB
не А
Полностью выполненное задание оценивается в 5 баллов;
4 операции – «4»; 3 операции – «3».
(Представители групп по очереди выходят к доске и отвечают).
За каждый правильный ответ (демонстрируется слайд)
команда получает -1 балл.
Оцените свою работу и сдайте консультанту.
III этап – Применение изученных знаний и способов деятельности (17 мин)
- Следующий этап нашего урока – практическая работа на компьютере. С помощью электронных таблиц выполните один из уровней предложенных заданий.
Постройте таблицы истинности для следующих формул:
Уровень 1 (по 1 баллу за каждое задание)
а)
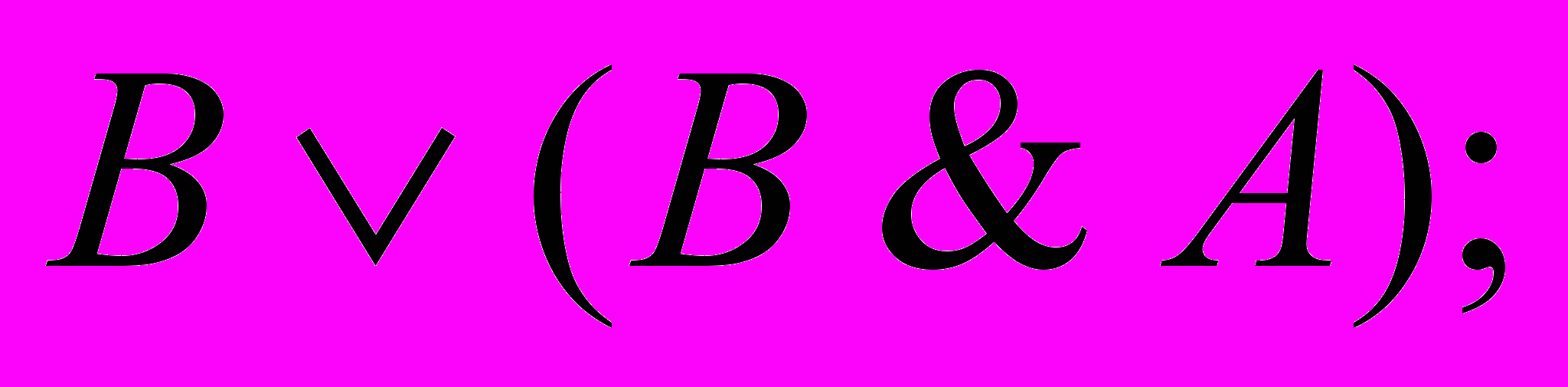
б)
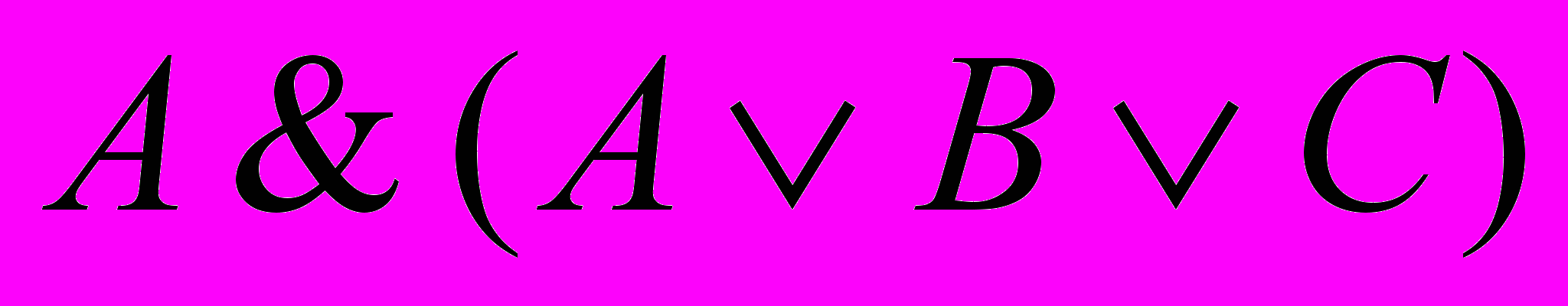 ;
; в)
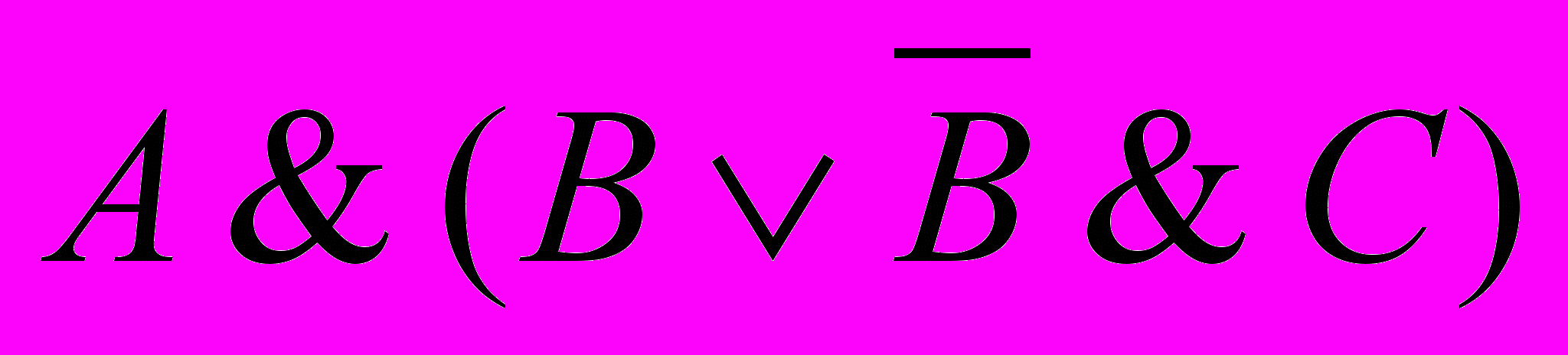 .
. Уровень II (по 2 балла за каждое задание)
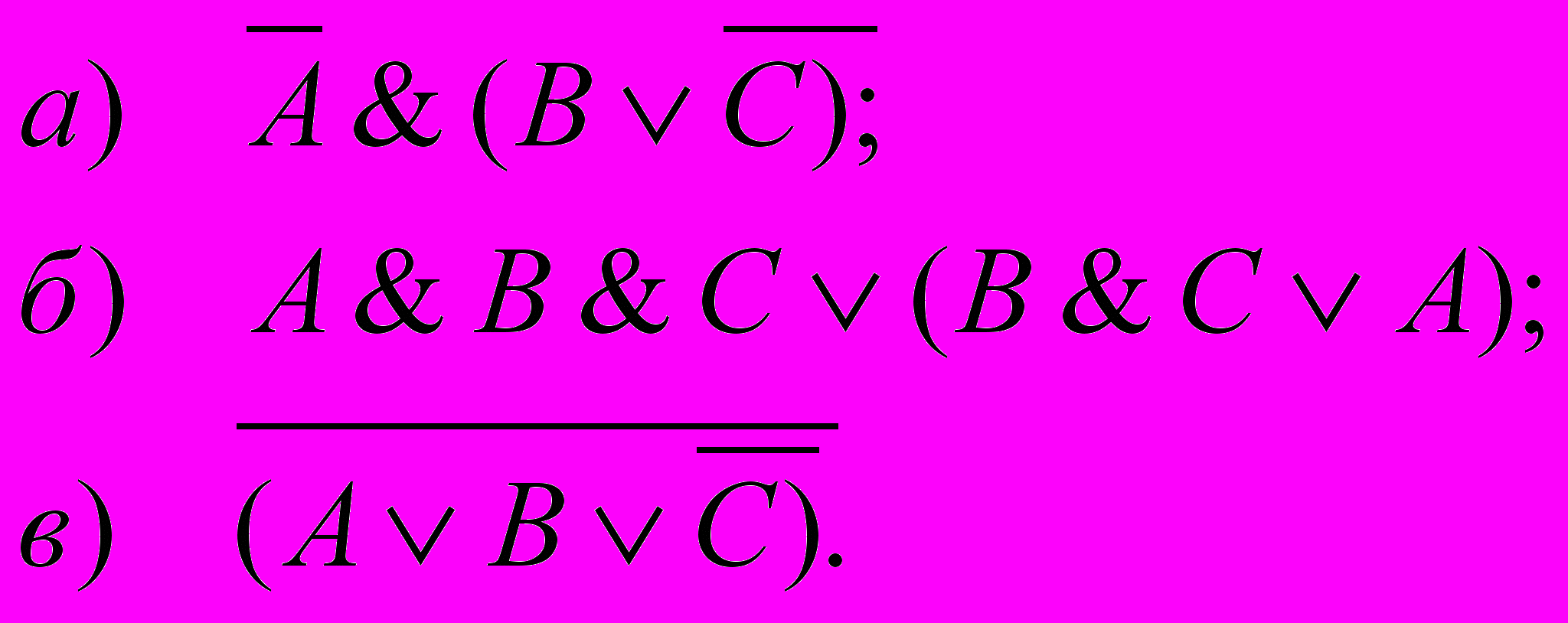
Консультанты проверьте работы своих членов группы.
Молодцы! Вы все справились с выбранными заданиями. Слайд 12
При работе за компьютером самым уязвимым органом является зрение. Чтобы снять усталость и зрительное напряжение проведем физкультминутку. Выполним гимнастику для глаз. Физкультминутка
Займите свои места за партами и оцените свою работу за компьютерами (отметьте свой результат в листах самооценки).
- Решение логических задач
Законы логики, правила преобразования логических выражений, умение составлять таблицы истинности довольно часто используются при решении задач из разных областей знаний: философии, юриспруденции, криминалистики, психологии и др. наук.
Я надеюсь, что ваши знания помогут справиться с предложенными логическими задачами.
«Кто есть кто?»
Задача 1
Определите, кто из подозреваемых участвовал в преступлении, если известно:
- если Иванов не участвовал или Петров участвовал, то Сидоров участвовал;
- если Иванов не участвовал, то Сидоров не участвовал.
- в преступлении участвовал только один из трех подозреваемых.
Ответ: Иванов.
Задача 2
Беседуют трое друзей: Белокуров, Рыжов и Чернов. Брюнет сказал
Белокурову: «Любопытно, что один из нас блондин, другой – брюнет,
третий - рыжий, но они у кого цвет волос не соответствует фамилии.» Какой цвет волос у каждого из друзей?
Ответ: Белокуров – рыжий, Рыжов- брюнет, Чернов – блондин.
Задача 3
В небольшом районном городе живут пять друзей: Иванов, Петренко, Сидорчук, Гришин и Капустин. Профессии у них разные: один из них маляр, другой - мельник, третий - плотник, четвертый - почтальон, а пятый – парикмахер.
Петренко и Гришин никогда не держали в руках малярной кисти.
Иванов и Гришин собираются посетить мельницу, на которой работает их товарищ.
Петренко и Капустин живут в одном доме с почтальоном.
Сидорчук был недавно в ЗАГСе одним из свидетелей, когда Петренко и дочь парикмахера сочетались законным браком.
Иванов и Петренко каждое воскресенье играют в городки с плотником и маляром.
Гришин и Капустин по субботам обязательно встречаются в парикмахерской, где работает их друг.
Почтальон предпочитает бриться сам.
Кто есть кто?
Ответ: Иванов – парикмахер, Петренко - мельник, Сидорчук –почтальон, Гришин - плотник, Капустин – маляр.
Проверьте, как вы справились с заданием. Отметьте результат в листе с/о.
- Логический лабиринт
Удобным способом представления логических выражений являются логические схемы. Работа интегральных схем на компьютерах основана на логических операциях, реализуемых базовыми логическими элементами.
Перед вами две схемы, на входы каждой из которых подаются Ноль и Единица. Выберите для себя одну схему и выясните, какой результат получается на выходе (Ноль или Единица).
Выполнение одной схемы оценивается 3 баллами, двух - 5 баллами.
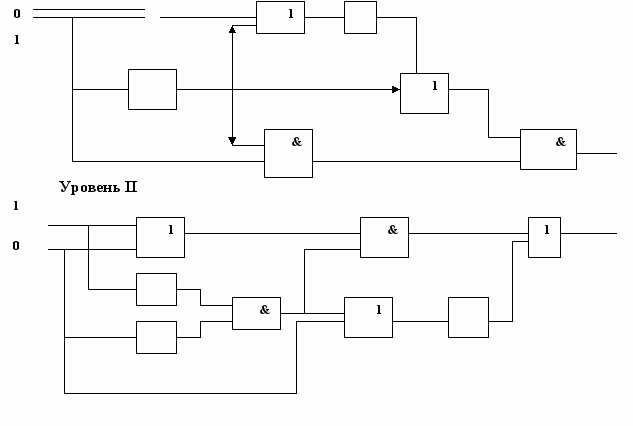
1
Уровень I
- Информационная минутка
(рассказ об ученых, внесших вклад в развитие Логики)
В это время консультанты групп подсчитывают количество баллов, набранных учащимися в ходе урока.
Логика в лицах.
Слово «логика» происходит от греческого «logos» и означает «мысль, мышление, речь, разум, смысл…». Основоположником логики считают древнегреческого философа Аристотеля, жившего в 384- 322 гг. до н.э. Он впервые систематизировал формы и правила мышления, подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления. Логика Аристотеля – это так называемая формальная логика и связана с анализом наших обычных содержательных рассуждений, выражаемых разговорным языком.
Со временем логика в своем развитии перешла от формальной к математической, в которой запись рассуждений осуществляется уже с помощью символов. В ней появились математические методы исследования, конкретность законов. Основоположником математической логики считают философа- математика Г.В. Лейбница , который жил в 1646- 1716 гг.
В XIX веке появился раздел математической логики – алгебра логики (алгебра высказываний). Алгебру логики в честь ее создателя, английского математика Дж. Буля, назвали булевой алгеброй. Булева алгебра нашла широкое практическое применение в технической области – при написании алгоритмов и программ, разработке электронных устройств, компьютеров, автоматических систем, в робототехнике и т.д.
VI. Домашнее задание
Тест в форме и по материалам ЕГЭ по информатике
V. этап – Прошли минуты совместного общения. Подведем итоги. (2 мин.) Консультанты озвучьте результат работы своей группы.
- Рефлексия (Заслушиваются мнения учащихся об уроке: Сегодня на уроке я …. Сегодня на уроке мы ….Урок прошел ….
Выберите поговорку соответствующую вашему настроению)
- А закончить наш урок мне хотелось бы словами Л. Кэрролла:
Овладев... методами «символической логики», вы получите увлекательное развлечение, не требующее ни специальных досок, ни карт, и к тому же полезное, независимо от того, чем вы занимаетесь. Методы эти позволяют вам обрести ясность мысли, способность находить собственное, оригинальное решение трудных задач, выработают у вас привычку к систематическому мышлению и, что особенно ценно, умение обнаруживать логические ошибки и находить изъяны и пробелы тех, кто не пытался овладеть увлекательным искусством логики.
- Так что ясных вам мыслей и оригинальных решений любых задач, с которыми вы будете сталкиваться в своей жизни.
- Урок окончен.
Лист самооценки
Ф.И. …………………………………………
| Этапы урока | Актуали-зация знаний | Практическая работа на ПК | Логическая схема | Решение логических задач | Общее кол-во баллов | Оценка за урок |
| Макс. кол-во баллов | 5 | I уровень – 3 II уровень - 6 | Одна – 3 Две - 5 |
| 22-30 15-21 9-14 | «5» «4» «3» |
| Набранное кол-во баллов | | | | | | |
Лист самооценки
Ф.И. …………………………………………
| Этапы урока | Актуали-зация знаний | Практическая работа на ПК | Логическая схема | Решение логических задач | Общее кол-во баллов | Оценка за урок |
| Макс. кол-во баллов | 5 | I уровень – 3 II уровень - 6 | Одна – 3 Две - 5 |
| 22-30 15-21 9-14 | «5» «4» «3» |
| Набранное кол-во баллов | | | | | | |
Лист самооценки
Ф.И. …………………………………………
| Этапы урока | Актуали-зация знаний | Практическая работа на ПК | Логическая схема | Решение логических задач | Общее кол-во баллов | Оценка за урок |
| Макс. кол-во баллов | 5 | I уровень – 3 II уровень - 6 | Одна – 3 Две - 5 |
| 22-30 15-21 9-14 | «5» «4» «3» |
| Набранное кол-во баллов | | | | | | |
