Н. П. Огарева математический факультет кафедра дифференциальных уравнений рабочая программа
| Вид материала | Рабочая программа |
- Н. П. Огарева математический факультет кафедра дифференциальных уравнений рабочая программа, 34.27kb.
- Нахождение первых интегралов нелинейных дифференциальных уравнений является одной, 31.75kb.
- Методические рекомендации по подготовке к сдаче государственного экзамена Раздел «Математика», 38.2kb.
- Учебная программа по дисциплине дифференциальные уравнения крюковский, 87.43kb.
- Программа дисциплины "Обыкновенные дифференциальные уравнения" Специальность нм, курс, 35.01kb.
- Задача Коши для квазилинейных дифференциальных уравнений в частных производных первого, 30.67kb.
- Рабочая программа дисциплины (модуля) асимптотические методы решения дифференциальных, 19.29kb.
- «Анализ эффективности применения современных ит при решении дифференциальных уравнений», 223.28kb.
- Программа дисциплины Дифференциальные уравнения Семестр, 29.32kb.
- Kirgizistan-tüRKİye manas üNİversitesi ders biLGİ formu, 113.45kb.
МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
имени Н. П. Огарева
МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
РАБОЧАЯ ПРОГРАММА
СПЕЦИАЛЬНОЙ ДИСЦИПЛИНЫ
СДМ.02. Математическое моделирование
физических процессов
специализированная подготовка
магистра по направлению
510200 – прикладная математика
и информатика
2 семестр
количество часов – 136
лекции – 68
лабораторные занятия – 68
самостоятельная работа – 104
Составители:
профессор В.Н. Щенников,
доцент Г.А. Курносов
Отчетности
К/р – 2
Экзамены – 1
Утверждено на заседании
кафедры дифференциальных уравнений
протокол №9
«14» сентября 2006 г.
Зав. кафедрой, профессор
___________ В.Н. Щенников
^
Саранск 2006
График учебного процесса
| № недели | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Лекции, ч. | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Практические зан., ч. | | | | | | | | | | | | | |
| Лабораторные зан., ч. | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Межсессионный учет | | | | | | | | | | | | | |
| Экзамен | | ||||||||||||
| № недели | 14 | 15 | 16 | 17 | | | | | | | | | |
| Лекции, ч. | 4 | 4 | 4 | 4 | | | | | | | | | |
| Практические зан., ч. | | | | | | | | | | | | | |
| Лабораторные зан., ч. | 4 | 4 | 4 | 4 | | | | | | | | | |
| Межсессионный учет | | | | | | | | | | | | | |
| Экзамен | Во время сессии | ||||||||||||
^
1. ЦЕЛИ И ЗАДАЧИ СПЕЦКУРСА
Программа спецкурса отражает новые требования, предъявляемые к образованию современных математиков. Ее основное содержание базируется на требованиях к обязательному минимуму содержания образовательной программы подготовки выпускника высшей школы, утвержденным Государственным комитетом Российской Федерации по высшему образованию 18 августа 1993 года.
Большая насыщенность математикой многих научных дисциплин обеспечивает использование математических методов, усвоенных студентами в ходе предшествующей учебы.
Изучение спецкурса предполагает:
- освоение современных методов исследования инженерных задач;
- овладение основными численными методами и их применение при решении практических задач;
- закрепление приобретенных навыков разработки компьютерных программ;
- выработку умения самостоятельного пополнения знаний и проведения анализа прикладных задач математическими средствами.
Материал спецкурса изучается в течение одного семестра. На лекциях излагается содержание курса, раскрываются важнейшие понятия и методы. Лекционный материал сопровождается наглядными примерами из реальной практики. На лабораторных занятиях студенты закрепляют методологию решения инженерных задач, а также получают дополнительные разъяснения теоретических положений.
Важным фактором усвоения спецкурса и овладения его методами является самостоятельная работа студентов. Ее эффективность обеспечивается системой контроля, включающей в себя регулярные консультации по тематике выполняемых исследований.
В ходе изучения спецкурса студенты выполняют небольшую научно-исследовательскую работу, по результатам которой оформляется научный отчет. Он оформляется в соответствии с действующими государственными стандартами и затем защищается студентами на основе приобретенных знаний.
^ 2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
2.1. ЛЕКЦИОННЫЕ ЗАНЯТИЯ
| № п/п | Наименование тем и их содержание | Количество лекционных часов |
| 1 | 2 | 3 |
| 1. | Общие сведения об объектах моделирования. Физическое и математическое моделирование. Основные принципы построения и требования к математическим моделям. Способы построения математических моделей. Статистический (экспериментальный) и теоретический методы построения математических моделей. Основные этапы экспериментального моделирования и их характеристики. Анализ и оптимизация математических моделей. Вычислительный эксперимент. Недостатки экспериментального моделирования. | 2 |
| 2. | ЗАДАЧА ОБ ОСТЫВАНИИ КОФЕ. Основные понятия. Алгоритм Эйлера. Программа для компьютера. Программа для решения задачи об остывании кофе. Устойчивость и точность. Простейшая графика. Перспектива. | 4 |
| 3. | ПАДЕНИЕ ТЕЛ. Основные понятия. Сила, действующая на падающее тело. Численное решение уравнений. Одномерное движение. Двумерные траектории. Другие приложения. | 4 |
| 4. | ЗАДАЧА КЕПЛЕРА. Уравнения движения планет. Движение по окружности. Эллиптические орбиты. Астрономические единицы. Замечания по программированию. Численное моделирование орбиты. Возмущения. Пространство скоростей. Солнечная система в миниатюре. | 4 |
| 5. | КОЛЕБАНИЯ. Простой гармонический осциллятор. Численное моделирование гармонического осциллятора. Математический маятник. Замечания по программированию. Затухающие колебания. Линейный отклик на внешнюю силу. Принципы суперпозиции. Колебания в электрических цепях. Численное интегрирование уравнений Ньютона. | 4 |
| 1 | 2 | 3 |
| 6. | ДИНАМИКА СИСТЕМ МНОГИХ ЧАСТИЦ. Потенциал межмолекулярного взаимодействия. Численный алгоритм. Краевые условия. Программа молекулярной динамики. Измерение макроскопических величин. Простые свойства переноса. Дополнительные сведения. Вириал давления. | 4 |
| 7. | ХАОТИЧЕСКОЕ ДВИЖЕНИЕ ДИНАМИЧЕСКИХ СИСТЕМ. Простое одномерное отображение. Удвоение периода. Универсальные свойства нелинейных отображений. Хаотическое поведение в классической механике. Двумерное отображение. Устойчивость неподвижных точек. | 4 |
| 8. | ВОЛНОВЫЕ ЯВЛЕНИЯ. Связанные осцилляторы. Фурье-анализ. Волновое движение. Интерференция и дифракция. Поляризация. Геометрическая оптика. | 4 |
| 9. | СТАТИСТИЧЕСКИЕ ПОЛЯ ЗАРЯДОВ И ТОКОВ. Электрические поля и потенциал. Магнетизм и силовые линии магнитного поля. Численное решение уравнения Лапласа. Дополнительные сведения. | 4 |
| 10. | ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ. Простые одномерные методы численного интегрирования. Численное интегрирование многих интегралов. Вычисление интегралов простейшим методом Монте-Карло. Вычисление многомерных интегралов методом Монте-Карло. Анализ погрешности метода Монте-Карло. Неравномерные распределения вероятностей. Выборка по значимости. Методы случайного блуждания. Оценки погрешностей численного интегрирования. Аналитический вывод стандартного отклонения от среднего. Метод отбора-отказа. | 4 |
| 11. | СЛУЧАЙНОЕ БЛУЖДАНИЕ. Одномерное случайное блуждание. Обобщения метода случайных блужданий. Приложения в физике полимеров. Непрерывный предел. Случайные числа. Метод наименьших квадратов. | 4 |
| 12. | ЗАДАЧА О ПЕРКОЛЯЦИИ. Порог перколяции. Маркировка кластеров. Критические показатели и конечномерное масштабирование. Ренорм-группа. | 4 |
| 13. | ФРАКТАЛЫ, МОДЕЛИ КИНЕТИЧЕСКОГО РОСТА И КЛЕТОЧНЫЕ АВТОМАТЫ. Фрактальная размерность. Регулярные фракталы и самоподобие. Процессы роста фракталов. Клеточные автоматы. | 4 |
| 14. | ПРИБЛИЖЕНИЕ К РАВНОВЕСИЮ. Простая модель. Точный перебор. Метод Монте-Карло. Энтропия. Влияние корреляций. Равновесная энтропия. Энтропия и хаос. | 4 |
| 15. | МИКРОКАНОНИЧЕСКИЙ АНСАМБЛЬ. Микроканонический ансамбль. Моделирование методом Монте-Карло. Одномерный классический идеальный газ. Температура и канонический ансамбль. Модель Изинга. Поток тепла. Связь средней энергии демона с температурой. | 4 |
| 16. | МОДЕЛИРОВАНИЕ КАНОНИЧЕСКОГО АНСАМБЛЯ МЕТОДОМ МОНТЕ-КАРЛО. Канонический ансамбль. Алгоритм Метрополиса. Проверка распределения Больцмана. Моделирование двумерной модели Изинга. Фазовый переход Изинга. Другие применения модели Изинга. Моделирование классических жидкостей. Другие приложения. Флуктуации в каноническом ансамбле. Точный расчет модели Изинга для решетки 2х2. | 4 |
| 17. | КВАНТОВЫЕ СИСТЕМЫ. Обзор квантовой теории. Стационарное уравнение Шредингера. Нестационарное уравнение Шредингера. Анализ квантовых систем с помощью метода случайных блужданий. Вариационные методы Монте-Карло для квантовомеханических систем. | 4 |
| 18. | Единство физики. Перколяция и галактики. Как компьютеры влияют сегодня на физику? | 2 |
^ 2.1. ЛАБОРАТОРНЫЕ ЗАНЯТИЯ
| № п/п | Наименование тем и их содержание | Количество часов |
| 1. | Работа над программами COOL (закон остывания Ньютона), COOLER (усовершенствованная версия программы COOL): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 2. | Работа над программами FALL (движение свободно падающего тела), STYROFOAM (движение свободно падающего тела с учетом сопротивления воздуха): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 3. | Работа над программами PLANET (движение планеты), PLANET2 (движение двух взаимодействующих планет): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 4. | Работа над программами SHO (простой гармонический осциллятор), PENDULA (мультипликация линейного и нелинейного маятников), RC (моделирование RC-цепи), BEEMAN (алгоритм Бимана для движения частицы в потенциале Морза): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 5. | Работа над программой MD (молекулярная динамика для потенциала Леннарда-Джонса): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 6. | Работа над программами MAP_TABLE (табулирование итераций стандартного отображения), MAP_PLOT (график итераций стандартного отображения), MAP_GRAF (граф стандартного отображения, получаемый с помощью рекурсии), NONLINEAR (хаотическое движение нелинейного маятника): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 7. | Работа над программами OSCILLATORS (N связанных осцилляторов), FOURIER (сложение фурье-гармоник), WAVES (волновое движение), INTERFERE (интерференция и дифракция волн), POLARIZE (поляризация света), FERMAT (принцип Ферма): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 8. | Работа над программами FIELDLINE (силовые линии электрического поля), MAGNETISM (силовые линии магнитного поля), LAPLACE (решение уравнения Лапласа методом релаксации): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 9. | Работа над программами INTEG (вычисление одномерного интеграла методом прямоугольников), INTEG2 (двумерное численное интегрирование), RANDOM (употребление генератора случайных чисел): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 10. | Работа над программами RANDOM_WALK (одномерное случайное блуждание), RANDOM_WALK2 (двумерное случайное блуждание), LATTICE_GAS (моделирование двумерного решеточного газа методом Монте-Карло): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 11. | Работа над программами SITE (рисование конфигураций ячеечной перколяции), CONTINUUM (рисование конфигураций непрерывной перколяции), CLUSTER (маркировка кластеров ячеечной перколяции и расчет характеристик кластеров), RG (визуализация ренорм-группы): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 12. | Работа над программами SINGLE_CLUSTER (рост уединенного перколяционного кластера), KOCH (генерирование треугольной кривой Коха), INVASION (образование оккупирующего перколяционного кластера): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 13. | Работа над программами BOX (моделирование частицы в ящике методом Монте-Карло), ENTROPY (метод подсчета совпадений Ма): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 14. | Работа над программами IDEAL_DEMON (моделирование идеального газа в микроканоническом ансамбле методом Монте-Карло), ISING_DEMON (моделирование одномерной модели Изинга методом Монте-Карло), CONDUCT (моделирование одномерной модели Изинга с тепловым потоком методом Монте-Карло): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 15. | Работа над программами BOLTZMANN (алгоритм Метрополиса для одномерной классической частицы), ISING (алгоритм Метрополиса для двумерной модели Изинга), HARD_DISK (алгоритм Метрополиса для жестких дисков): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 16. | Работа над программами EIGEN (вычисление энергетических уровней и собственных функций в одномерном случае), WAVEPACKET (демонстрация движения волнового пакета), QMWALK (анализ уравнения Шредингера методом случайного блуждания), VARIATION (вариационный расчет основного состояния методом Монте-Карло): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
| 17. | Работа над программой GALAXY (перколяционная модель формирования галактики): ввод исходного текста, отладка, исследование физических процессов методом вычислительного эксперимента с помощью варьирования параметров и изменения алгоритма. | 4 |
^ 3. ТРЕБОВАНИЯ К УРОВНЮ УСВОЕНИЯ ПРОГРАММЫ И ФОРМЫ ТЕКУЩЕГО КОНТРОЛЯ
На экзамене оценка «отлично» выставляется студенту, который:
1) глубоко и прочно усвоил программный материал в полном объеме, исчерпывающе, грамотно и логически стройно его излагает, четко формулирует основные понятия, приводит соответствующие примеры, уверенно владеет методологией курса, свободно ориентируется в его внутренней структуре, четко выявляет межпредметные связи с другими учебными дисциплинами;
2) умеет творчески иллюстрировать теоретические положения курса примерами, самостоятельно придумывает такие примеры, применять теоретические знания к решению практических задач;
3) хорошо владеет современными методами исследования, способен к самостоятельному пополнению и обновлению знаний, понимает прикладную направленность курса математики.
Оценка «хорошо» выставляется студенту, который:
1) твердо усвоил программный материал, грамотно и по существу излагает его без существенных ошибок, правильно применяет теоретические положения при решении конкретных задач, с небольшими погрешностями приводит формулировки определений, не допускает существенных неточностей при выборе и обоснованности математических методов;
2) владеет методологией математики и методами исследования, устанавливает внутренние и межпредметные связи, умеет увязывать теорию с практикой;
3) по ходу изложения допускает небольшие пробелы, не искажающие содержания ответа.
Оценка «удовлетворительно» выставляется студенту, который не совсем твердо владеет программным материалом, знает основные теоретические положения изучаемого курса, обладает достаточными для продолжения обучения и предстоящей профессиональной деятельности, знаниями. Выполняет текущие задания, устанавливаемые графиком учебного процесса. При ответах допускает малосущественные погрешности, искажения логической последовательности при изложении материала, неточную аргументацию теоретических положений курса, испытывает затруднения при решении достаточно сложных задач.
Оценка «неудовлетворительно» выставляется студенту, имеющему серьезные пробелы в знании учебного материала, допускающему принципиальные ошибки при выполнении предусмотренных программой контрольных заданий. Уровень знаний недостаточен для дальнейшей учебы и будущей профессиональной деятельности.
^
ОСНОВНАЯ ЛИТЕРАТУРА
1. Аппель П. Теоретическая механика. — М.: Физматгиз, 1960.
2. Базаров И. П., Геворкян Э. В., Николаев П. Н. Неравновесная термодинамика и физическая кинетика. — М.: Изд-во МГУ, 1989.
3. Бэрдсол Ч., Ленгдон А. Физика плазмы и численное моделирование. — М.: Энергоатомиздат, 1989.
4. Вильсон К., Когут Дж. Ренормализационная группа и
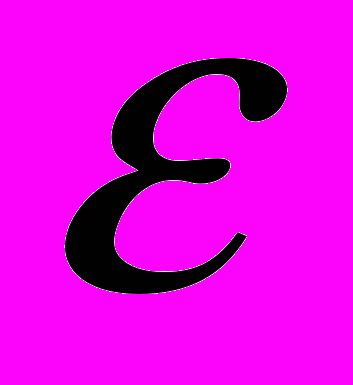-разложения. — М.: Мир, 1975. 5. Голдстейн Г. Классическая механика. — М.: Мир, 1974.
6. Гросберг А. Ю., Хохлов А. Р. Статистическая физика макромолекул. — М.: Наука, 1989.
7. Гросберг А. Ю., Хохлов А. Р. Физика в мире полимеров. — М.: Наука, 1989.
8. Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Ч. 1: Пер. с англ. — М.: Мир, 1990. — 352 с.
9. Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Ч. 2: Пер. с англ. — М.: Мир, 1990. — 400 с.
10. Гутер Р. С., Овчинский Б. В. Элементы численного анализа и математической обработки результатов опыта. — М.: Наука, 1970.
11. Дайсон Ф., Монтролл Э., Кац М., Фишер М. Устойчивость и фазовые переходы. — М.: Мир, 1982.
12. Жаблон К., Симон Ж.-К. Применение ЭВМ для численного моделирования в физике. — М.: Наука, 1983. — 240 с.
13. Киттель Ч. Введение в физику твердого тела. — М.: Наука, 1978.
14. Климонтович Ю. Л. Статистическая физика. — М.: Наука, 1982.
15. Кнут Д. Искусство программирования на ЭВМ. Т. 2. — М.: Мир, 1979.
16. Компьютеры, модели, вычислительный эксперимент. Введение в информатику с позиций математического моделирования. — М.: Наука, 1988. — 176 с.
17. Косевич А. М., Ковалев А. С. Введение в нелинейную физическую механику. — Киев: Наукова думка, 1989.
18. Крайнов А. В., Мигдал А. Б. Качественные методы в квантовой механике. — М.: Наука, 1976.
19. Крауфорд Ф. Волны. — М.: Мир, 1975.
20. Кунин С. Вычислительная физика: Пер. с англ. — М.: Мир, 1992. — 520 с.
21. Кунц К. С. Численный анализ. — Киев: Технiка, 1964.
22. Лагарьков А. Н., Сергеев В. М. Метод молекулярной динамики в статистической физике // УФН, Т. 125, Вып. 3, 1978. — С. 400-448.
23. Любарский Г. Я., Слабоспяцкий Р. П., Хажмурадов М. А., Адушкина Р. И. Математическое моделирование и эксперимент. — Киев: Наукова думка, 1987. — 160 с.
24. Мандельштам И. Л. Лекции по теории колебаний. — М.: Наука, 1972.
25. Матвеев А. Н. Механика и теория относительности. — М.: Высшая школа, 1986.
26. Матвеев А. Н. Молекулярная физика. — М.: Высшая школа, 1981.
27. Матвеев А. Н. Электричество и магнетизм. — М.: Высшая школа, 1983.
28. Метод статистических испытаний / Под ред. Ю. А. Шнейдера. — М.: Физматгиз, 1962.
29. Методы Монте-Карло в статистической физике / Под ред. М. Калоса. — М.: Мир, 1984.
30. Методы Монте-Карло в статистической физике / Под ред. К. Биндера. — М.: Мир, 1982.
31. Мигдал А. Б. Качественные методы в квантовой теории. — М.: Наука, 1975.
32. Николис Дж. Динамика иерархических систем: эволюционное представление. — М.: Мир, 1989.
33. Перселл Э. Электричество и магнетизм. — М.: Мир, 1982.
34. Пирс Дж. Почти все о волнах. — М.: Мир, 1976.
35. Пресс В. П., Фланнери Б. П., Тьюкольски С. А., Веттерлинг В. Т. Численные рецепты. — М.: Мир, 1990.
36. Райф Ф. Статистическая физика. — М.: Наука, 1986.
37. Сивухин Д. В. Оптика. — М.: Наука, 1985.
38. Сивухин Д. В. Электричество и магнетизм. — М.: Наука, 1986.
39. Соболь И. М. Численные методы Монте-Карло. — М.: Наука, 1973.
40. Странные аттракторы. Новое в зарубежной науке: Математика, Вып. 22. — М.: Мир, 1981.
41. Тейлор Дж. Введение в теорию ошибок. — М.: Мир, 1985.
42. Фейгенбаум М. Универсальное поведение нелинейных систем // УФН, Т. 141. Вып. 3. 1978. — С. 343-374.
43. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике: Пер. с англ. — М.: Мир, 1966.
44. Флюгге К. Задачи по квантовой механике. — М.: Наука, 1973.
45. Хенон М. Двумерное отображение со странным аттрактором // Странные аттракторы. — М.: Мир, 1981.
46. Хокни Р., Иствуд Дж. Численное моделирование методом частиц. — М.: Мир, 1987.
47. Хуанг К. Статистическая механика. — М.: Мир, 1966.
48. Чандрасекар С. Стохастические проблемы в физике и астрономии. — М.: ИЛ, 1947.
49. Шифф Л. Квантовая механика. — М.: ИЛ, 1959.
50. Шкловский Б. И., Эфрос А. Л. Электронные свойства легированных полупроводников. — М.: Наука, 1979.
51. Шустер Г. Детерминированный хаос: Введение. — М.: Мир, 1988.
52. Эфрос А. Л. Физика и геометрия беспорядка. — М.: Наука, 1982.