Учебная программа по дисциплине дифференциальные уравнения крюковский А. С
| Вид материала | Программа |
- Программа-минимум кандидатского экзамена по специальности 01. 01. 02 «Дифференциальные, 37.38kb.
- Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
- Календарный план чтения лекций, 27.51kb.
- Программа курса "Дифференциальные уравнения " для специальности 010400 "Физика", 36.39kb.
- Обыкновенные дифференциальные уравнения, 17.54kb.
- Программа по курсу «Дифференциальные уравнения», 41.77kb.
- Уравнения математической физики направление подготовки, 18.02kb.
- Вопросы к экзамену по учебной дисциплине «Дифференциальные уравнения», 32.43kb.
- Л. С. Понтрягин Обыкновенные дифференциальные уравнения М., «Наука», 1974, 31.21kb.
- Календарный план учебных занятий по обязательной дисциплине «Обыкновенные дифференциальные, 87.8kb.
УЧЕБНАЯ ПРОГРАММА ПО ДИСЦИПЛИНЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Крюковский А.С.
| Цели преподавания дисциплины: | ||||||||||||
| Формирование у студентов знаний терминологии и основных понятий дифференциальных уравнений, основных принципов и подходов к решению дифференциальных уравнений. | ||||||||||||
| Перечень дисциплин, усвоение которых студентам необходимо для усвоения курса | ||||||||||||
| «Математический анализ» | ||||||||||||
| В результате изучения курса студент должен | ||||||||||||
| знать: | ||||||||||||
| ||||||||||||
| уметь: | ||||||||||||
| ||||||||||||
| иметь представление о: | ||||||||||||
| ||||||||||||
| Основными видами занятий являются лекции и практические занятия. | ||||||||||||
| Основыными видами промежуточного контроля знаний являются: выполнение промежуточных индивидуальных заданий и контрольное домашнее задание. | ||||||||||||
| Основными видами рубежного контроля знаний являются зачет | ||||||||||||
| | ||||||||||||
| Часы, отведенные на изучение дисциплины, согласно учебному плану (151ч):
| ||||||||||||
| СОДЕРЖАНИЕ КУРСА | ||||||||||||
| Тема 1. Теорема коши | ||||||||||||
| Задача Коши. Теорема существования и единственности решения задачи Коши. Условие Липшица. Доказательство теоремы существования решения (в рамках теоремы Коши) для дифференциального уравнения вида 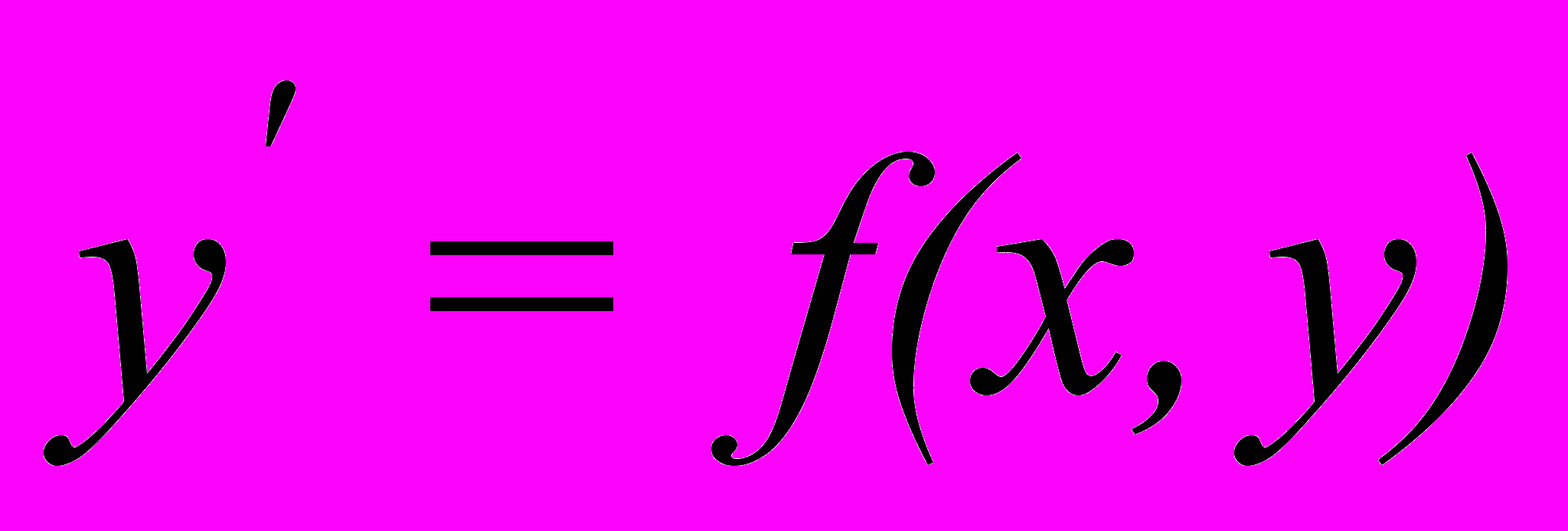 . Доказательство теоремы о единственности решения (в рамках теоремы Коши) для дифференциального уравнения вида . Доказательство теоремы о единственности решения (в рамках теоремы Коши) для дифференциального уравнения вида 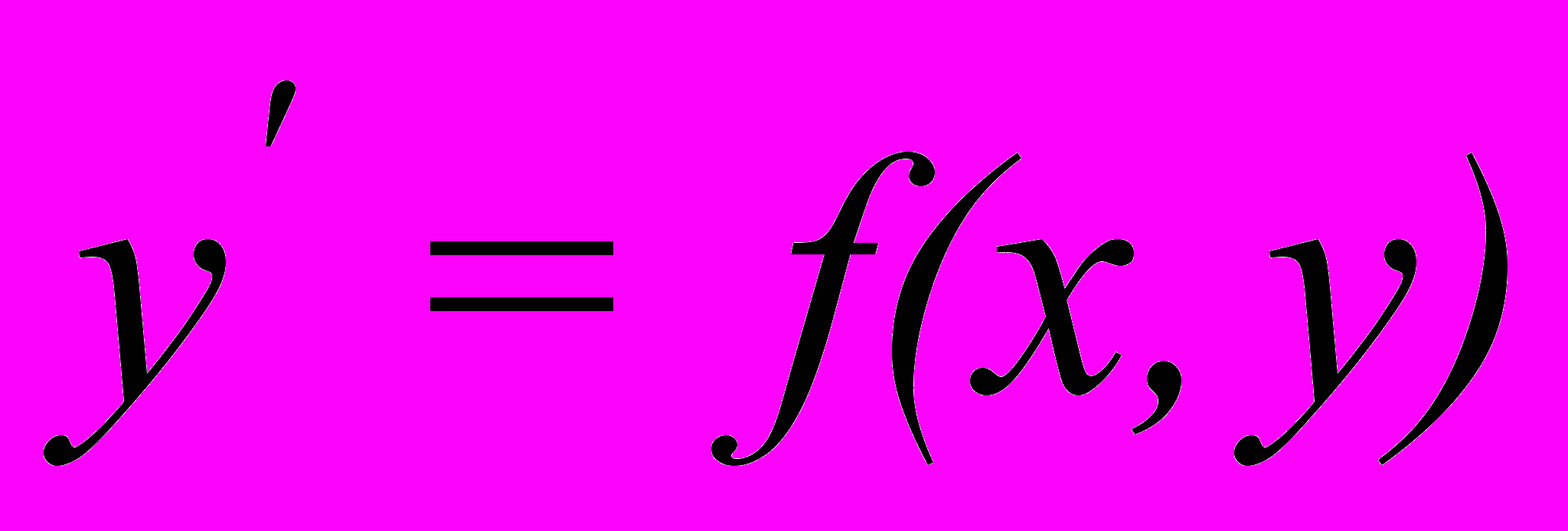 . . | ||||||||||||
| | ||||||||||||
| Тема 2. Дифференциальные уравнения первого порядка, разрешенные относительно производной | ||||||||||||
| Обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными. Дифференциальные уравнения первого порядка вида 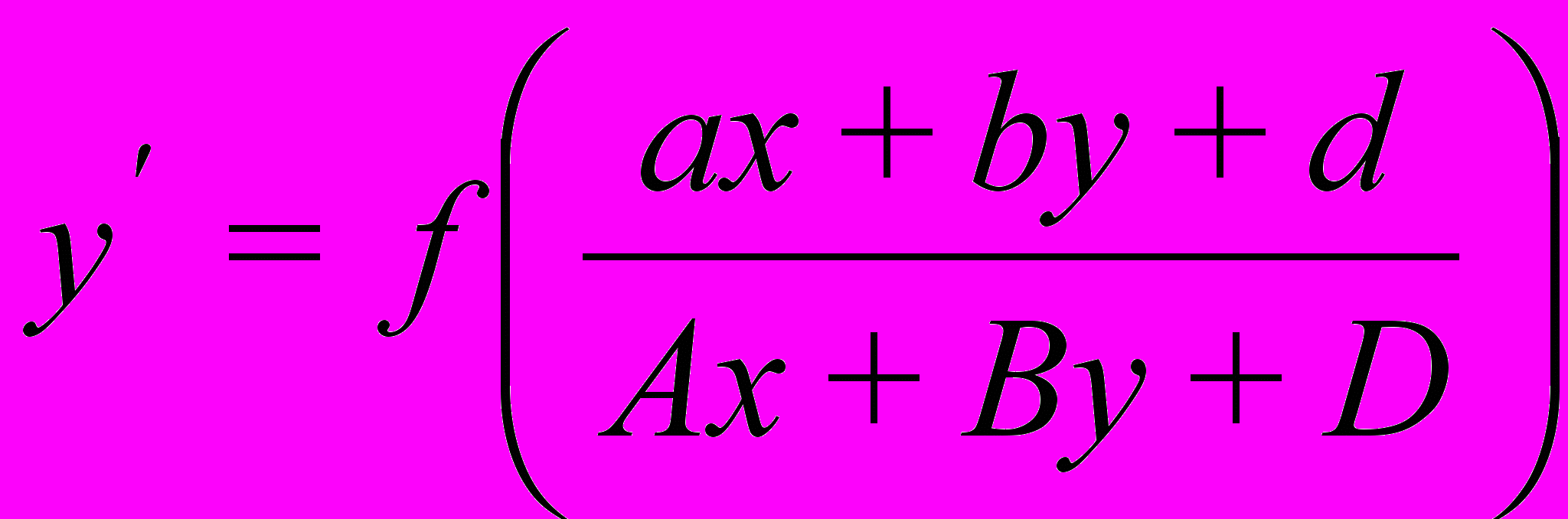 . Уравнения в полных дифференциалах. Решение обыкновенных однородных дифференциальных уравнений первого порядка. Решение обыкновенных неоднородных линейных дифференциальных уравнений первого порядка. Уравнение Бернулли. Уравнение Риккати. . Уравнения в полных дифференциалах. Решение обыкновенных однородных дифференциальных уравнений первого порядка. Решение обыкновенных неоднородных линейных дифференциальных уравнений первого порядка. Уравнение Бернулли. Уравнение Риккати. | ||||||||||||
| Тема 3. Дифференциальные уравнения первого порядка, не разрешенные относительно производной | ||||||||||||
| Теорема о существовании и единственности решения дифференциального уравнения первого порядка, не разрешенного относительно производной. Особые решения обыкновенных дифференциальных уравнений, не разрешенных относительно производной. Обыкновенные дифференциальные уравнения, не разрешенные относительно производной, вида 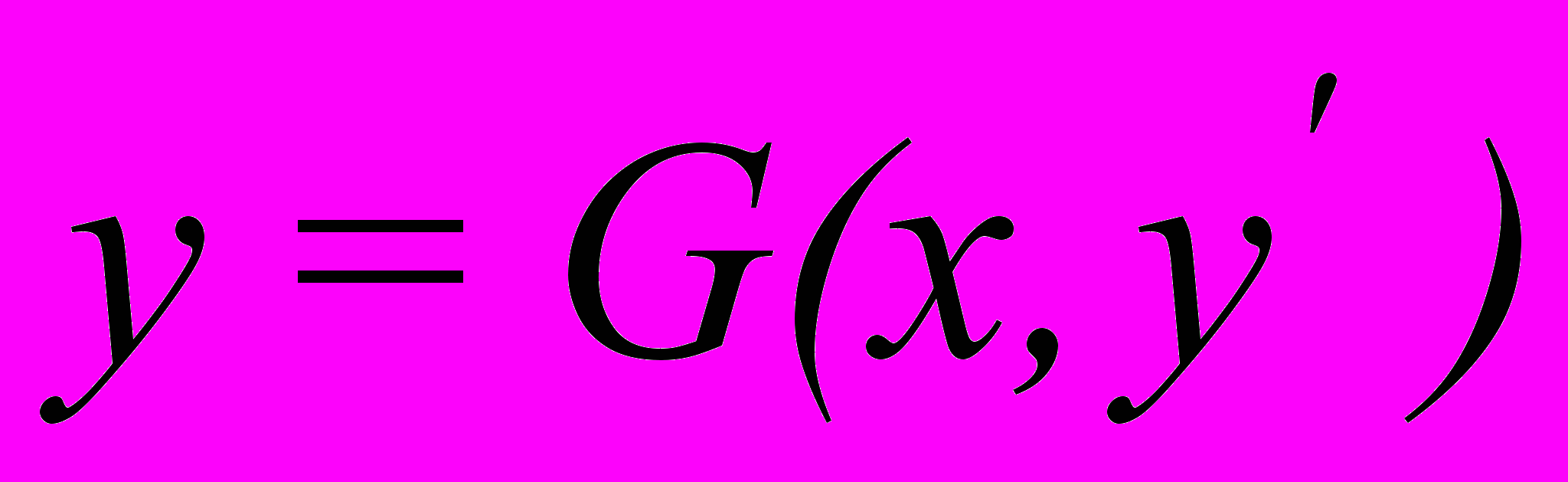 . Обыкновенные дифференциальные уравнения, не разрешенные относительно производной, вида . Обыкновенные дифференциальные уравнения, не разрешенные относительно производной, вида 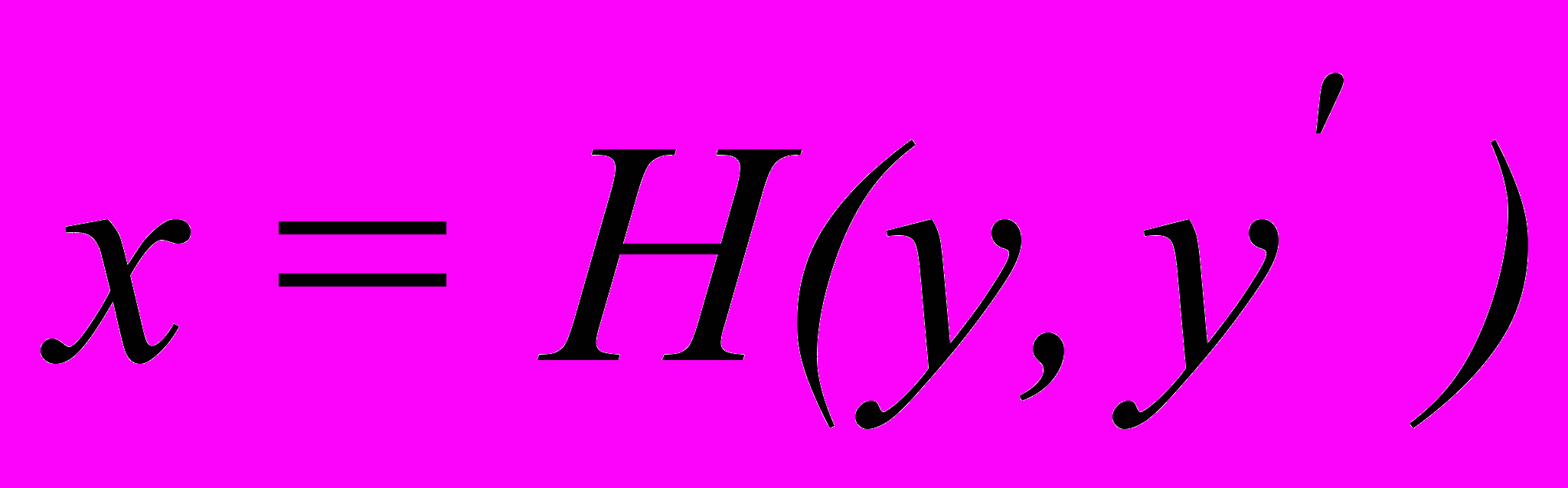 . . | ||||||||||||
| Тема 4. Линейные дифференциальные уравнения n-ого порядка с переменными коэффициентами | ||||||||||||
| Линейная зависимость и независимость функций. Определитель Вронского. Фундаментальная система решений линейного дифференциального уравнения n-ого порядка с переменными коэффициентами. Формула Лиувилля для линейного дифференциального уравнения n-ого порядка с переменными коэффициентами. Определение частного решения линейного дифференциального уравнения n-ого порядка с переменными коэффициентами. | ||||||||||||
| Тема 5. Линейные дифференциальные уравнения с постоянными коэффициентами | ||||||||||||
| Теория решения линейных дифференциальных уравнений с постоянными коэффициентами (общее решение и частное решения). Решение однородных обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами. Характеристическое уравнение, фундаментальная система решений, общее решение. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами, нахождение общего решения методом вариации произвольной постоянной. Решение однородных обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами (все корни характеристического уравнения действительные и различные). Решение однородных обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами (корни характеристического уравнения действительные и кратные). Решение однородных обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами (у характеристического уравнения существуют не кратные комплексные корни). Решение однородных обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами (существуют кратные комплексные корни характеристического уравнения). Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью вида: 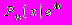 в случае, когда не является корнем характеристического уравнения. Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью вида: в случае, когда не является корнем характеристического уравнения. Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью вида: 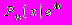 в случае, когда – корень характеристического уравнения. Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью вида: в случае, когда – корень характеристического уравнения. Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью вида: 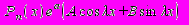 в случае, когда ( в случае, когда (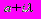 ) не является корнем характеристического уравнения. Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью вида: ) не является корнем характеристического уравнения. Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами и с правой частью вида: 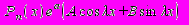 в случае, когда ( в случае, когда (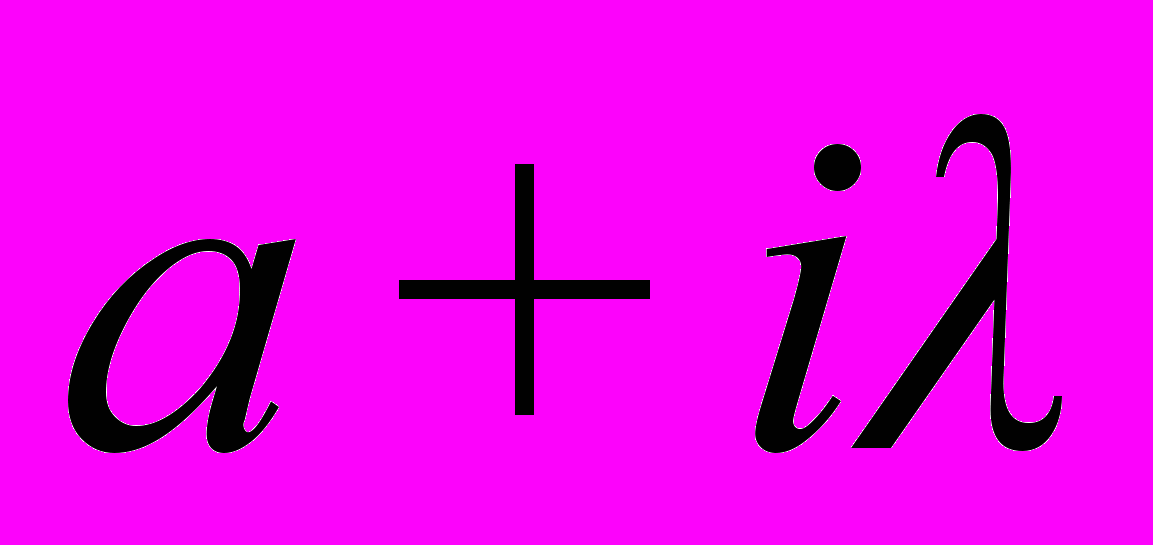 ) является корнем характеристического уравнения. ) является корнем характеристического уравнения. | ||||||||||||
| Тема 6. Уравнения Эйлера | ||||||||||||
| Решение однородных уравнений Эйлера (все корни характеристического уравнения действительные и различные). Решения однородных уравнений Эйлера (корни характеристического уравнения действительные и кратные). Решения однородных уравнений Эйлера (существуют не кратные комплексные корни характеристического уравнения). Решения однородных уравнений Эйлера (существуют кратные комплексные корни характеристического уравнения). Решение неоднородных уравнений Эйлера с правой частью вида 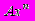 в случае, когда n не является корнем характеристического уравнения. Решение неоднородных уравнений Эйлера с правой частью вида в случае, когда n не является корнем характеристического уравнения. Решение неоднородных уравнений Эйлера с правой частью вида 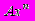 в случае, когда n является корнем характеристического уравнения. в случае, когда n является корнем характеристического уравнения. | ||||||||||||
| Тема 7. Разностные уравнения | ||||||||||||
| Решение однородных линейных разностных уравнений с постоянными коэффициентами (все корни характеристического уравнения действительные и различные). Решение однородных линейных разностных уравнений с постоянными коэффициентами (корни характеристического уравнения действительные и кратные). Решение линейных разностных уравнений с постоянными коэффициентами и с правой частью вида 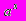 в случае, когда a не является корнем характеристического уравнения. Решение линейных разностных уравнений с постоянными коэффициентами и с правой частью вида в случае, когда a не является корнем характеристического уравнения. Решение линейных разностных уравнений с постоянными коэффициентами и с правой частью вида 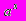 в случае, когда a является корнем характеристического уравнения. в случае, когда a является корнем характеристического уравнения. | ||||||||||||
| Тема 8. Системы дифференциальных уравнений | ||||||||||||
| Нормальные системы дифференциальных уравнений. Векторная запись нормальной системы. Задача Коши для нормальной системы обыкновенных дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Автономные системы. Линейные системы дифференциальных уравнений. Свойства решений. Линейная зависимость и независимость системы вектор–функций. Определитель Вронского. Фундаментальная система решений системы линейных дифференциальных уравнений. Формула Лиувилля для системы линейных дифференциальных уравнений с переменными коэффициентами. Определение частного решения неоднородной системы линейных дифференциальных уравнений с переменными коэффициентами методом вариации постоянных. Решение автономных систем линейных дифференциальных уравнений первого порядка с постоянными коэффициентами. Решение систем неоднородных линейных дифференциальных уравнений первого порядка с постоянными коэффициентами. | ||||||||||||
| Тема 9. Положения равновесия | ||||||||||||
| Классификация типов положений равновесия автономных систем линейных дифференциальных уравнений второго порядка. Геометрический смысл решения. Фазовое пространство (плоскость), фазовая кривая. Линеаризация автономной системы дифференциальных уравнений второго порядка в окрестности положения равновесия типа «узел». Линеаризация автономной системы дифференциальных уравнений второго порядка в окрестности положения равновесия типа «седло». Линеаризация автономной системы дифференциальных уравнений второго порядка в окрестности положения равновесия типа «фокус». Исследование автономной системы дифференциальных уравнений второго порядка в окрестности негрубых положений равновесия. Фазовые траектории автономной системы линейных дифференциальных уравнений второго порядка в окрестности положения равновесия типа «центр». Устойчивость по Ляпунову положений равновесия. Первый метод Ляпунова. Второй метод Ляпунова исследования устойчивости положений равновесия. Функция Ляпунова. | ||||||||||||
| Тема 10. Основы вариационного исчисления Основные понятия вариационного исчисления: постановка задачи. Дифференцируемые функционалы; необходимое условие экстремума. Простейшая задача вариационного исчисления. Уравнение Эйлера-Лагранжа. Задача со свободными концами. Функционалы от вектор-функций. Принцип Гамильтона. Вариационный вывод уравнения колебаний. Исследование квадратичного функционала. Вторая вариация и условие экстремума. | ||||||||||||
| Тема 11. Основы теории интегральных уравнений Интегральные уравнения: классификация, ядро интегрального оператора, характеристические числа и собственные функции, сопряженные уравнения. Эрмитовы ядра интегральных уравнений. Альтернатива Фредгольма. Решение уравнения Фредгольма II рода методом резольвент. Интегральное уравнение Абеля. Решение уравнения Фредгольма II рода с вырожденным ядром. Решение уравнения Вольтерра II рода с разностным ядром, сведение уравнения Вольтерра II рода с разностным ядром рода к задаче Коши для обыкновенного дифференциального уравнения. Решение уравнения Вольтерра II рода с помощью резольвент. Резольвенты некоторых интегральных уравнений Вольтерра. | ||||||||||||
| Тема 12. Основы теории дифференциальных уравнений в частных производных Дифференциальные уравнения в частных производных первого порядка. Решение линейных дифференциальных уравнений первого порядка в частных производных методом разделения переменных. Метод суперпозиции при решении дифференциальных уравнений в частных производных. Сведение дифференциального уравнения в частных производных первого порядка к системе обыкновенных дифференциальных уравнений. Полные интегралы дифференциальных уравнений в частных производных первого порядка. Классификация линейных дифференциальных уравнения в частных производных второго порядка. Решение задачи Коши для дифференциального уравнения второго порядка параболического типа, формула Пуассона. Решение задачи Коши для дифференциального уравнения второго порядка гиперболического типа, формула Даламбера. Решение смешанной задачи для дифференциального уравнения второго порядка параболического типа. Решение смешанной для дифференциального уравнения второго порядка эллиптического типа. Функция Бесселя. | ||||||||||||
| ЛИТЕРАТУРА | ||||||||||||
| | ||||||||||||
| Основная: | ||||||||||||
| | ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| | ||||||||||||
| | ||||||||||||
| Дополнительная: | ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
|
