Программа курса "Дифференциальные уравнения " для специальности 010400 "Физика"
| Вид материала | Программа курса |
СодержаниеПояснительная записка. II. Дифференциальные уравнения порядка выше первого. IV. Вопросы устойчивости. V. Уравнения в частных производных первого порядка. |
- Рабочая программа «Механика и основы механики сплошных сред» Специальность 010400 физика,, 141.09kb.
- Рабочая программа по курсу «дифференциальные уравнения» для специальности 010400 «Физика», 209.38kb.
- Программа-минимум кандидатского экзамена по специальности 01. 01. 02 «Дифференциальные, 37.38kb.
- Программа курса элементы общей теории относительности объем: лекции 50 часов Кафедра, 56.38kb.
- Вопросы к экзамену по курсу «Дифференциальные уравнения», 22.85kb.
- Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
- Программа по дисциплине Физика элементарных частиц для специальности 010400 «Физика, 115.04kb.
- Программа по дисциплине «Квантовая теория» для специальности 010400 -«Физика» реализуемых, 265.52kb.
- Календарный план чтения лекций, 27.51kb.
- Программа дисциплины "общая физика" для специальности 010400 " физика " (вечернее отделение), 361.38kb.
Рабочая программа
курса “Дифференциальные уравнения ” для специальности 010400 “Физика”
Факультет: физико - математический
Кафедра: математического анализа
Курс: II
Отделение: дневное
Лекции: 32 часов
Практические занятия: 32 часа
Всего: 64 часов
Рабочая программа обсуждена на заседании кафедры 08.09.2000 года
И.о. зав. кафедрой математического анализа _______________ доцент Редькина Т.В.
Одобрено Ученым советом физико - математического факультета
Председатель Совета ___________________________________ доцент Падалка В.В.
^ Пояснительная записка.
Программа составлена с учетом последовательности прохождения материала, определенной основными межпредметными связями с физическими курсами учебного плана, но с сохранением внутренней логики изложения дисциплины “Дифференциальные уравнения”.
Решение дифференциальных уравнений - основной аппарат общей и теоретической физики, а также методов математической физики.
Лектору , по согласованию с кафедрой, предоставляется право изменять последовательность прохождения отдельных тем. Практические занятия следует строить так, чтобы на каждом из них повторялся соответствующий теоретический материал и были выработаны основные навыки и умения , связанные с решением примеров и задач на уровне, необходимом для изучения физики. По данному курсу предусматривается проведение трех контрольных работ.
I. Дифференциальные уравнения первого порядка.
1. Основные понятия.
2. Задачи, приводящие к дифференциальным уравнениям.
3. Уравнения первого порядка, разрешенные относительно производной.
4. Уравнение с разделяющимися переменными.
5. Уравнения, приводящиеся к уравнениям с разделяющимися переменными.
6. Однородные уравнения.
7. Уравнения, приводящиеся к однородным.
8. Линейные уравнения первого порядка.
9. Уравнения Бернулли и Риккати.
10. Уравнения в полных дифференциалах.
11. Интегрирующий множитель.
12. Теоремы существования и единственности решения дифференциального уравнения
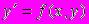 .
.13. Приближенные методы интегрирования уравнений первого порядка.
14. Уравнения, неразрешенные относительно производной.
15. Уравнения Лагранжа и Клеро.
16. Теорема существования и единственности для дифференциальных уравнений, неразрешенных относительно производной.
17. Особые решения. Расположение интегральных кривых в окрестности границы области D(x,y).
^ II. Дифференциальные уравнения порядка выше первого.
1. Теорема о существовании и единственности для дифференциалного уравнения п-ого порядка.
2. Простейшие случаи понижения порядка.
3. Линейные уравнения п-ого порядка.
4. Линейные однородные уравнения с постоянными коэффициентами и уравнения Эйлера.
5. Линейные неоднородные уравнения.
6. Линейные неоднородные уравнения с постоянными коэффициентами и уравнения Эйлера.
7. Интегрирование дифференциальных уравнений при помощи степенных рядов.
8. Метод малого параметра и его приложения в теории квазилинейных колебаний.
9. Понятие о краевых задачах.
III. Системы дифференциальных уравнений.
1. Общие понятия.
2. Интегрирование системы дифференциальных уравнений путем сведения к одному уравнению более высокого порядка.
3. Интегралы системы. Некоторые интегрируемые комбинации.
4. Общая теория однородных систем.
5. Неоднородная система.
6. Однородные линейные системы с постоянными коэффициентами.
7. Общее исследование системы.
8. Матричный метод.
9. Неоднородные линейные системы с постоянными коэффициентами.
10. Приближенные методы интегрирования систем дифференциальных уравнений и уравнений п-ого порядка.
^ IV. Вопросы устойчивости.
1. Устойчивость по Ляпунову.
2. Теорема Ляпунова.
3. Устойчивость решений линейных систем.
4. Линейные однородные системы с периодическими коэффициентами.
5. Второй метод Ляпунова.
^ V. Уравнения в частных производных первого порядка.
1. Основные понятия.
2. Линейные и квазилинейные уравнения в частных производных первого порядка.
3. Уравнение Пфаффа.
4. Нелинейные уравнения первого порядка.
Литература.
1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное ичисление.-М.:Наука,1965
2. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений.-М.:Наука,1964
3. Еругин Н.П. Книга для чтения по общему курсу дифференциальных уравнений.-М.:Наука и техника,1970
4. Малкин И.Г. Теория устойчивости движения.-М.:Гостехиздат ,1952
5. Степанов В.В. Курс дифференциальных уравнений.-М.:Физматгиз,1959
6. Арнольд В.И. Обыкновенные дифференциальные уравнения.-М.:Наука,1984
7. Пантрягин Л.С. Обыкновенные диференциальные уравнения.-М.:Наука,1970
8. Матвеев Н.М. Сборник задач по обыкновенным дифференциальным уравнениям.-М.:Высшая школа, 1987
9. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям.-М.:Наука,1979
10. Краснов М.Л., Киселев А.И., Макаренко Г.И. Сборник задач по обыкновенным дифференциальным уравнениям.-М.:Высшая школа,1978
Программу составил: доцент Баграмян В.А.
