Лекция Темы обсуждений предыдущей лекции

Вид материала

Лекция

Содержание Выдвинем основную гипотезу H Замечание 1. Если альтернативная гипотеза будет формулироваться следующим образом Основная и альтернативная гипотезы формулируются следующим образом Для дальнейших рассуждений нам понадобятся следующие понятия: оценка неизвестной дисперсии s При альтернативных гипотезах вида: вид H

Подобный материал:

• Лекция поведение потребителя, 61.41kb.
• Лекция 11. Основные вопросы, выносимые на обсуждение на предыдущей лекции, 91.29kb.
• Лекция 4 основы теории спроса и предложения, 43.74kb.
• Лекция Расчет основных термодинамических величин ΔU,, 283.92kb.
• Темы, которые мы обсуждали на предыдущей лекции: Прообраз=(Тадж Махал)=Неизвестный, 97.53kb.
• Урок истории в 6 классе, 18.18kb.
• В. В. Управление персоналом. М.: Академия, 2003. 528 с. Лекция, 1904.58kb.
• Изучение теоретической механики, 209.36kb.
• Темы обсуждений Врамках мероприятия затронуты следующие темы: -типичные административные, 14.73kb.
• Лекции и семинары проблемная лекция, 45.27kb.

Лекция 7.

Темы обсуждений предыдущей лекции:

1. Ввели понятие остатка:



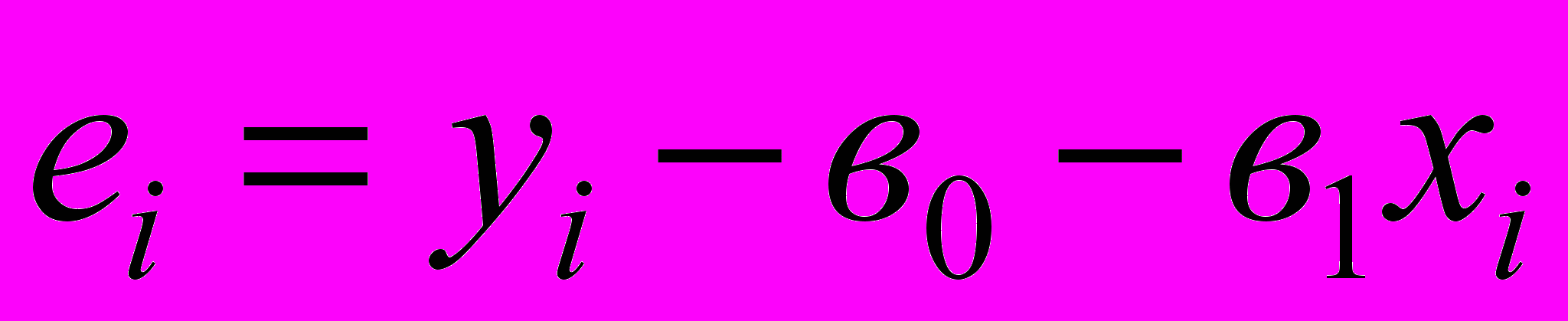
2.Доказали теорему:

TSS= RSS+ ESS.

3.Дали определение коэффициента детерминации:



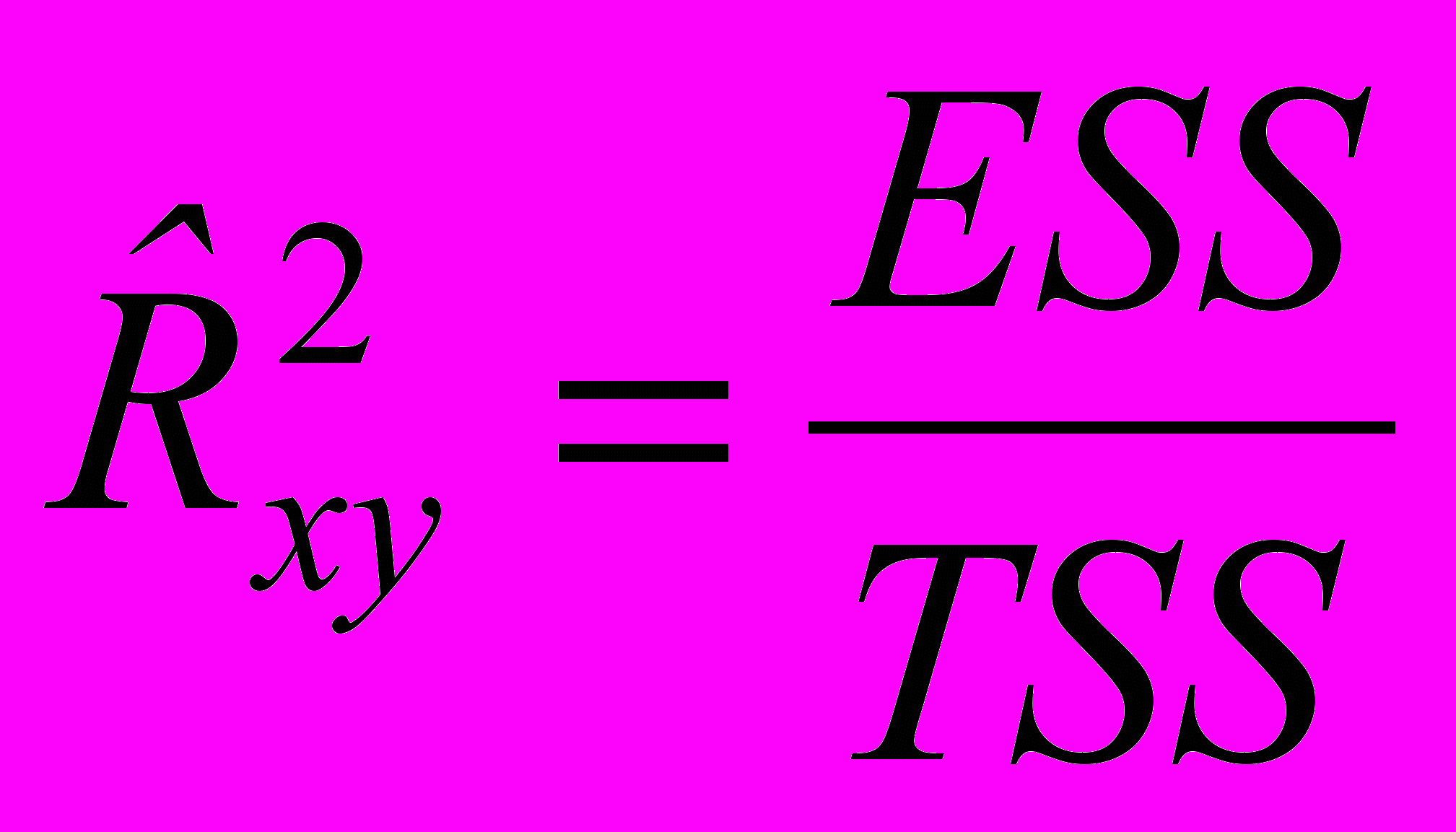
4. Отметили, что имеет место равенство:





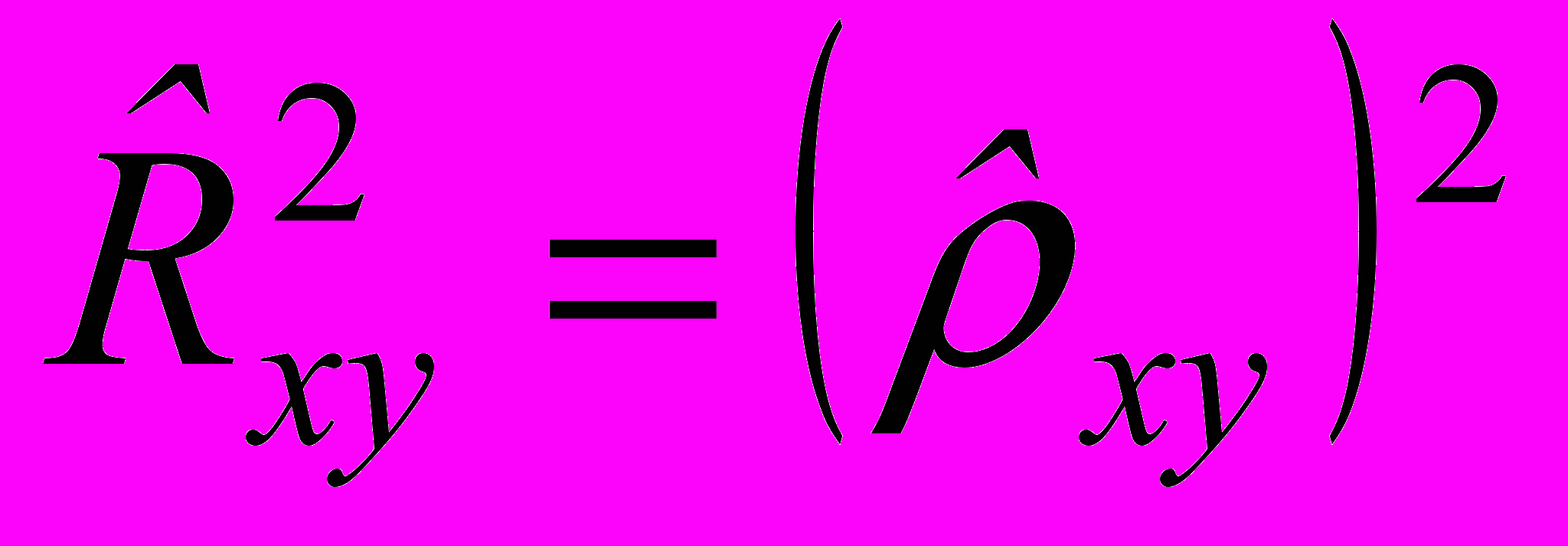
2.5. Анализ адекватности регрессионной модели эмпирическим данным


На этой лекции во-первых, рассмотрим каким образом, применяя статистическую проверку гипотез, можно проверить предположение о зависимости фактора x и результирующего признака y. Во-вторых, проведем проверку гипотезы о том, что функция, связывающая x и y, линейная.

Предположим, что переменная х в модели линейной регрессии носит случайный характер, причем ее закон распределения так же, как и у случайной составляющей модели, нормальный. В рамках этих предположений проверку гипотезы о независимости х и у сведем к проверке гипотезы о неокоррелируемости двух случайных величин. Как известно, для нормально распределенных случайных величин из некоррелируемости следует их независимость. Это позволит нам использовать коэффициент корреляции для оценки тесноты связи между двумя случайными величинами. Однако, как уже отмечалось выше и как указывается в [1]: «пока не предложено характеристики линейной связи, которая бы обладала очевидным преимуществом по сравнению с коэффициентом корреляции, его интерпретация оказывается часто весьма ненадежной».

Вычислим все выборочные числовые характеристики x и y и, самое главное, вычислим .

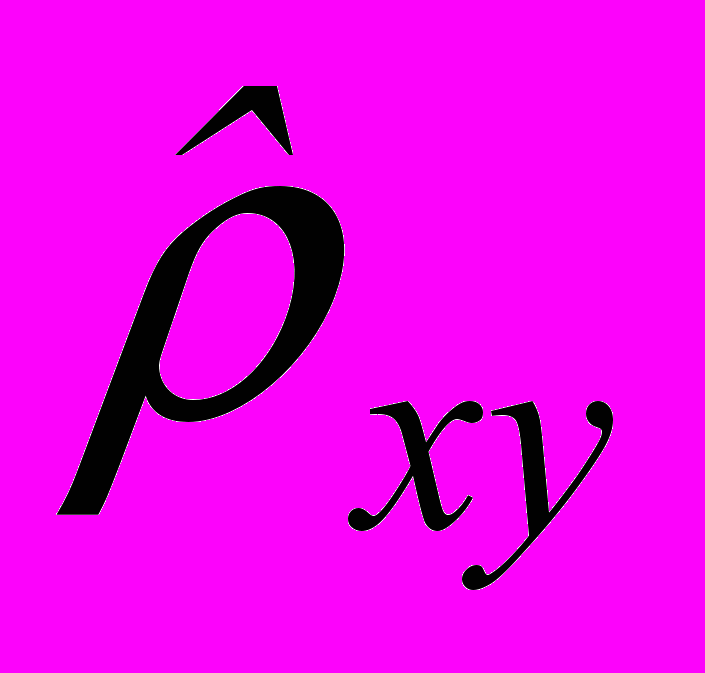^ Выдвинем основную гипотезу H₀ о том, что переменные x и y некоррелированные:

H₀:

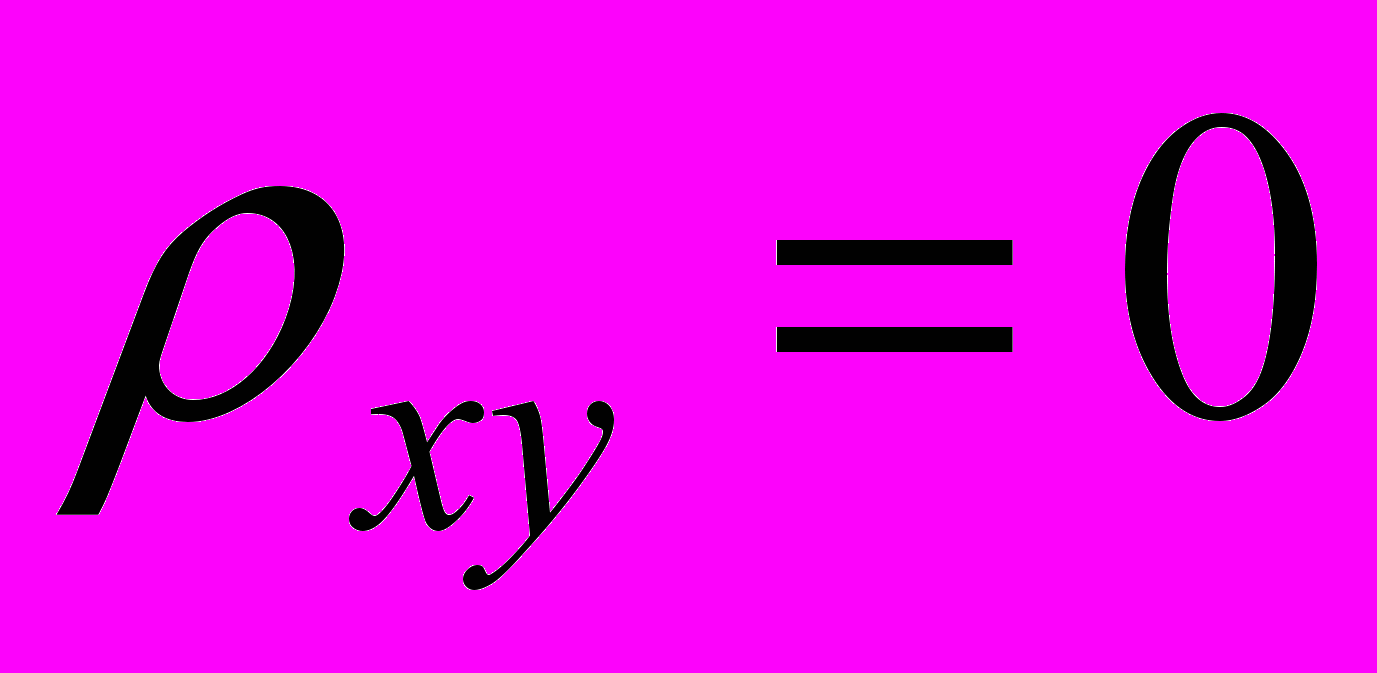
и альтернативную гипотезу H_а:

H_а: .

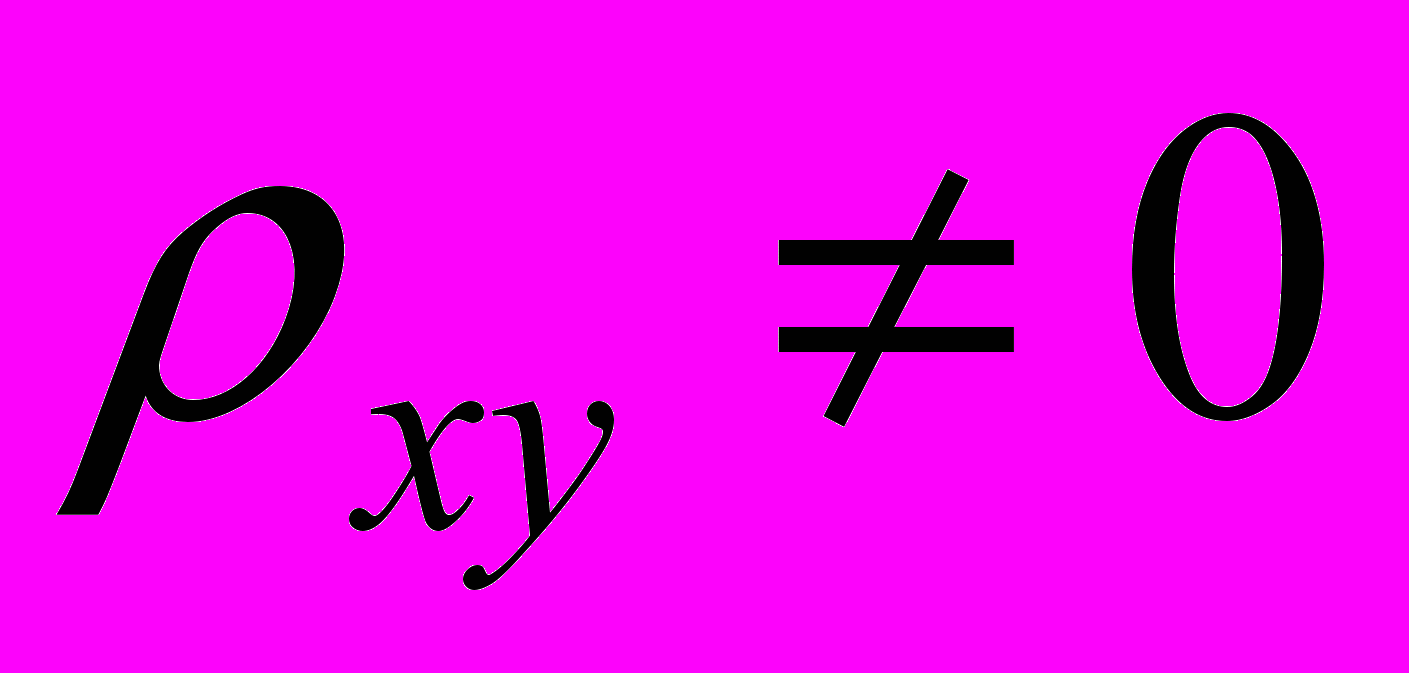Проверку гипотезы будем проводить, действуя согласно алгоритму, приведенному в параграфе 1.3. Для проверки гипотезы H₀ введем выборочную статистику:

Z*=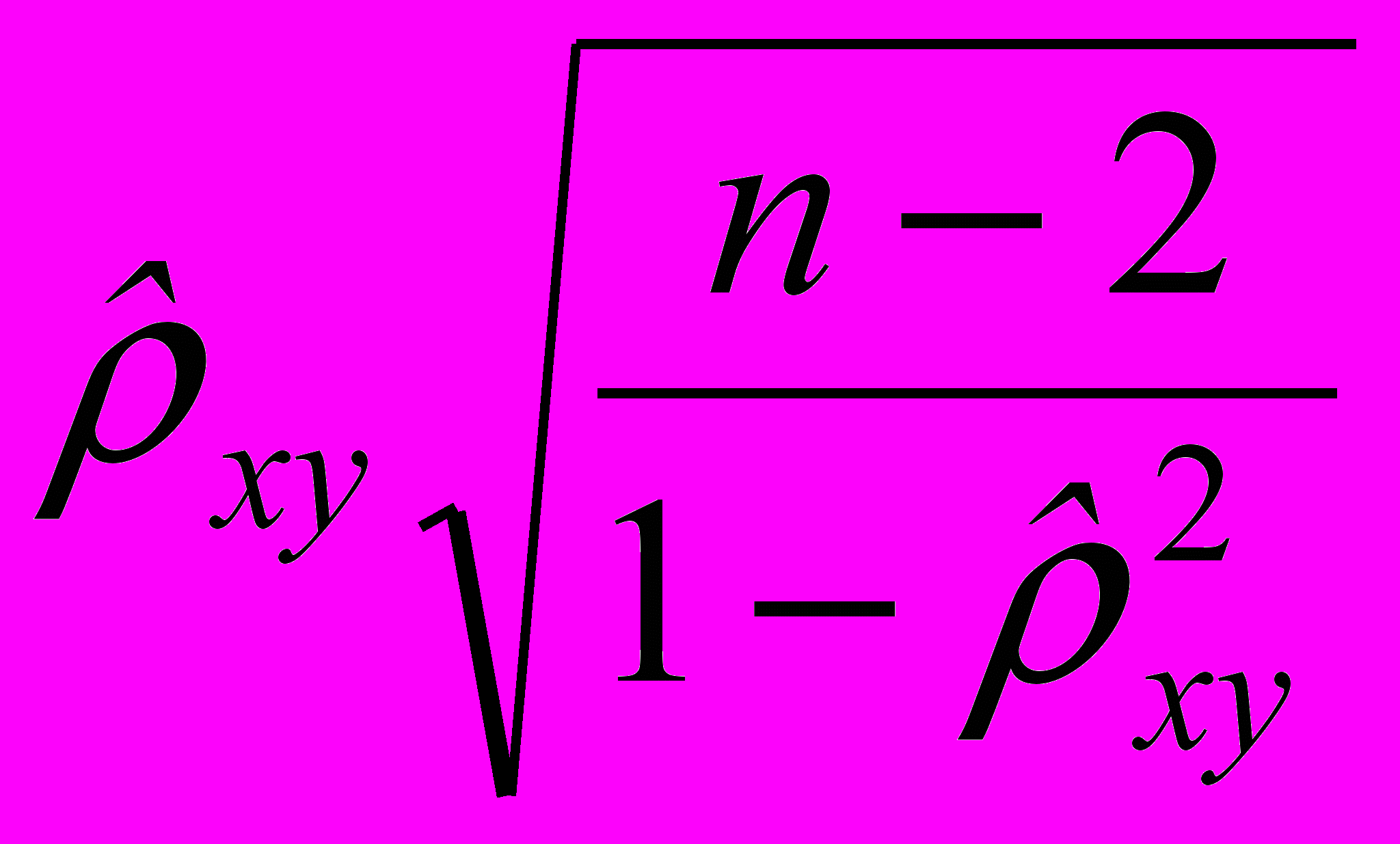. (2.5.1)

Доказано, что если основная гипотеза верна, то эта статистика распределена по закону Стьюдента (t-распределение) с (n-2) степенями свободы. Её часто называют t-статистикой. Используя таблицы распределения Стьюдента, по заданному уровню значимости и

(n-2) степеням свободы, находим границу двусторонней критической области К₂, К₁= - К₂.

Проверяем, если выполняется одно из неравенств Z*£ К₁ или

Z* ³ К₂, основную гипотезу отвергаем, принимаем альтернативную. В этом случае говорим, что у нас есть основание считать, что предположение о независимости случайных величин необоснованно.

В том случае, когда выборочная статистика удовлетворяет неравенству

К₁ < Z* <К₂ принимаем основную гипотезу и делаем вывод, что у нас нет оснований считать, что у зависит от х, либо зависимость носит нелинейный характер. Следовательно, когда принимаем основную гипотезу, нам следует или вообще отказаться от построения регрессионной модели между рассматриваемыми переменными, либо рассмотреть нелинейную модель.

^ Замечание 1. Если альтернативная гипотеза будет формулироваться следующим образом:

H_а: .

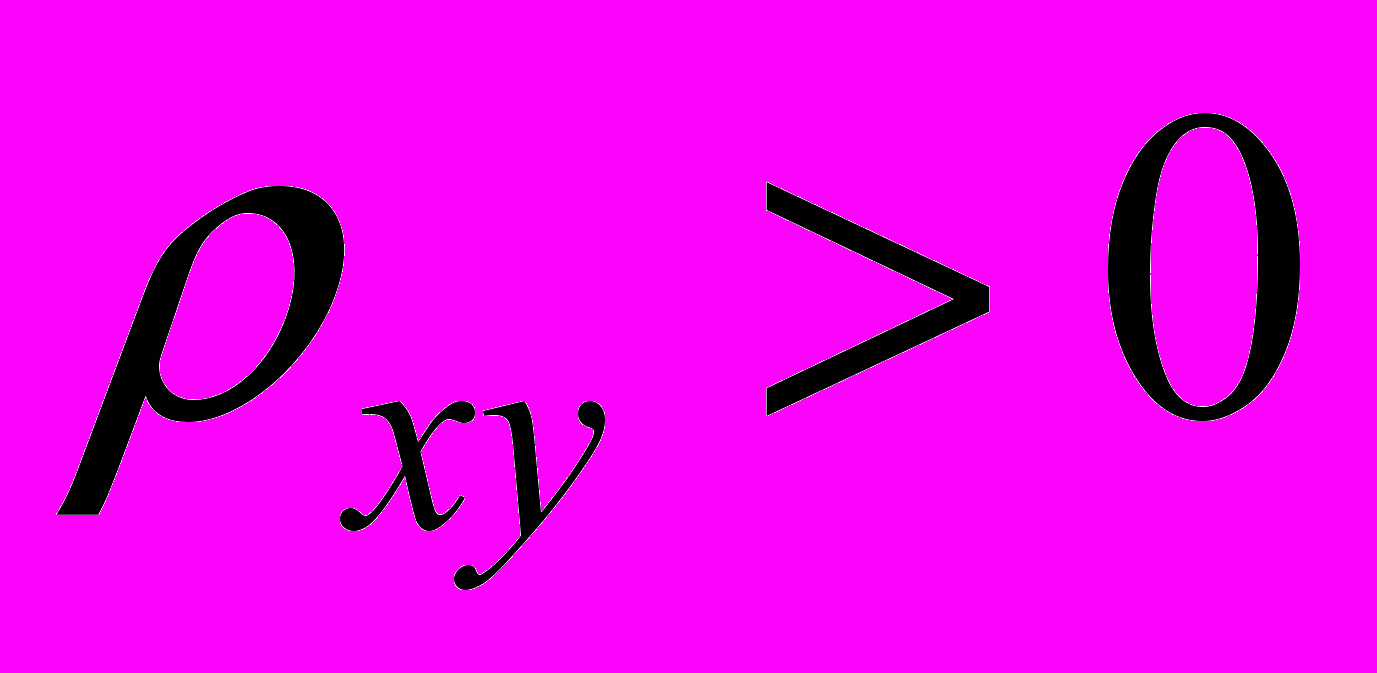или

H_а: ,

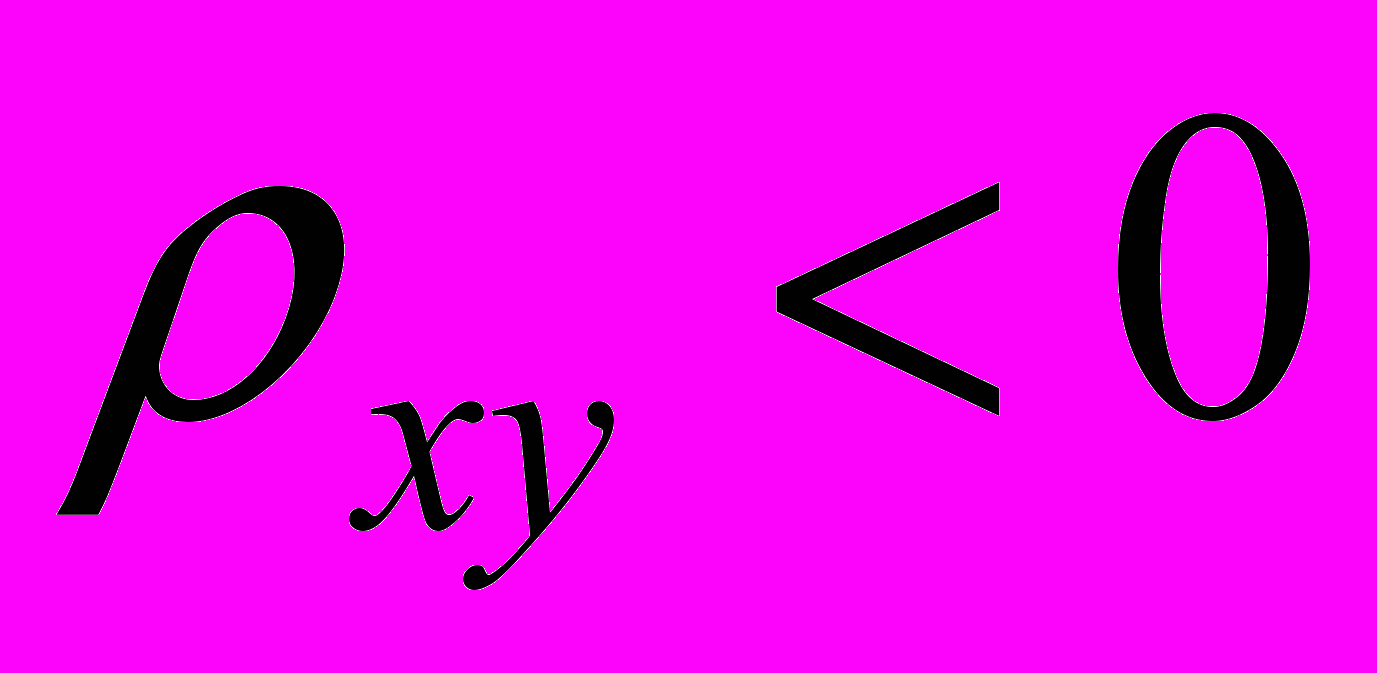то в первом случае критическая область будет правосторонней и гипотезу H_а будем принимать тогда, когда будет иметь место неравенство Z* ³ К₂. Если выборочная статистика будет удовлетворять неравенству Z*< К₂ , будем принимать основную гипотезу. Во втором случае критическая область будет левосторонней, поэтому альтернативная гипотеза будет приниматься тогда, когда выполняется неравенство Z*£ К₁. Основная гипотеза будет приниматься когда Z*> К₁.▲

Замечание 2. Качественное проведение статистических расчетов, требует, чтобы объем выборки, по которой они проводятся, был достаточно велик. Если объем информации недостаточен (выборка небольшого объема), то даже, тогда когда теоретический коэффициент 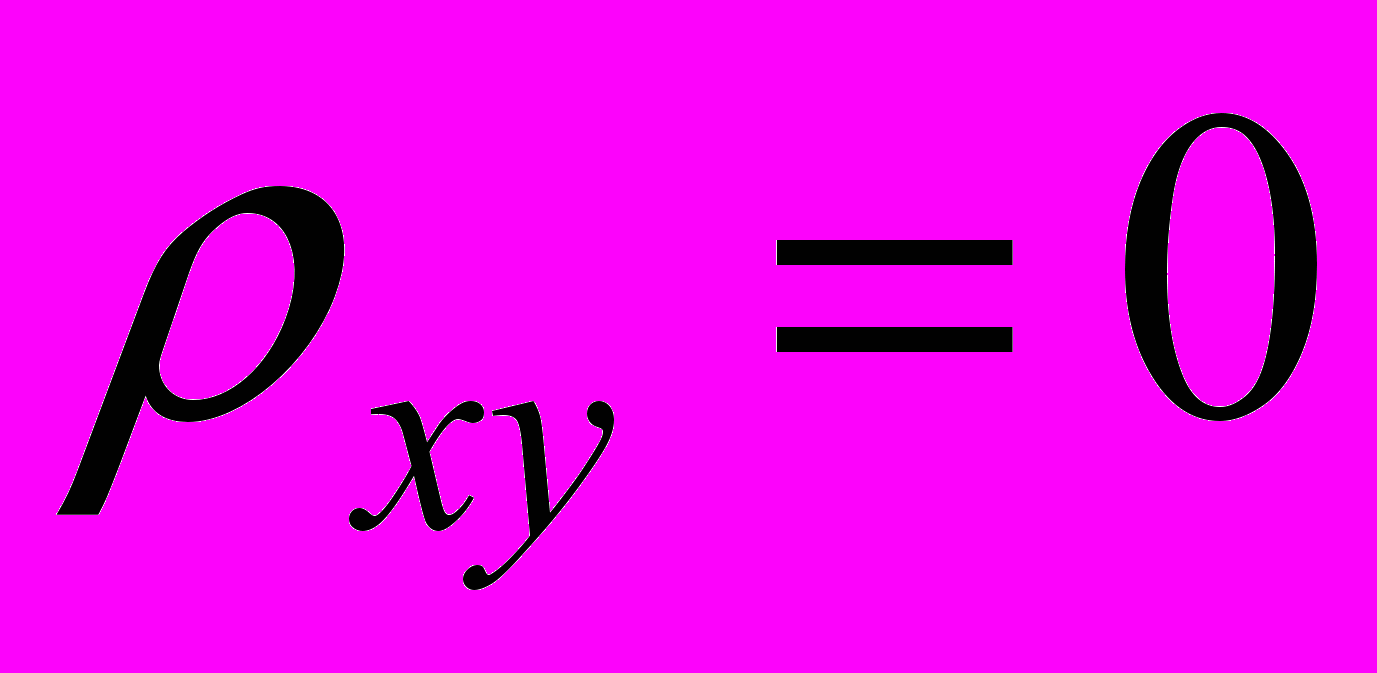(нормально распределенные случайные величины независимы), выборочный коэффициент корреляции может оказаться большой величиной и, на основании этого, мы можем сделать ошибочные выводы. Поэтому следует проверять значимость выборочного коэффициента корреляции, то есть проверять какую величину 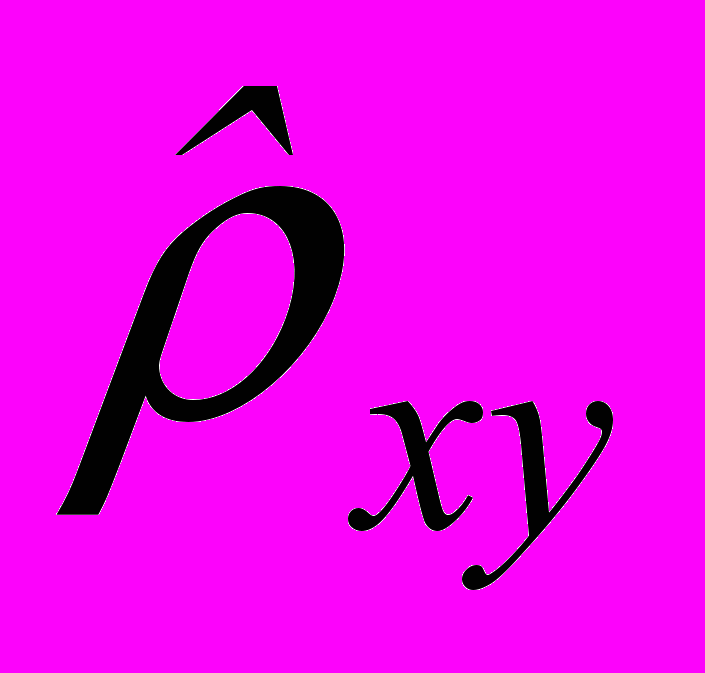следует считать достаточной для того, чтобы сделать обоснованный вывод о стохастической связи между х и у.

^ Основная и альтернативная гипотезы формулируются следующим образом:

H₀: ,

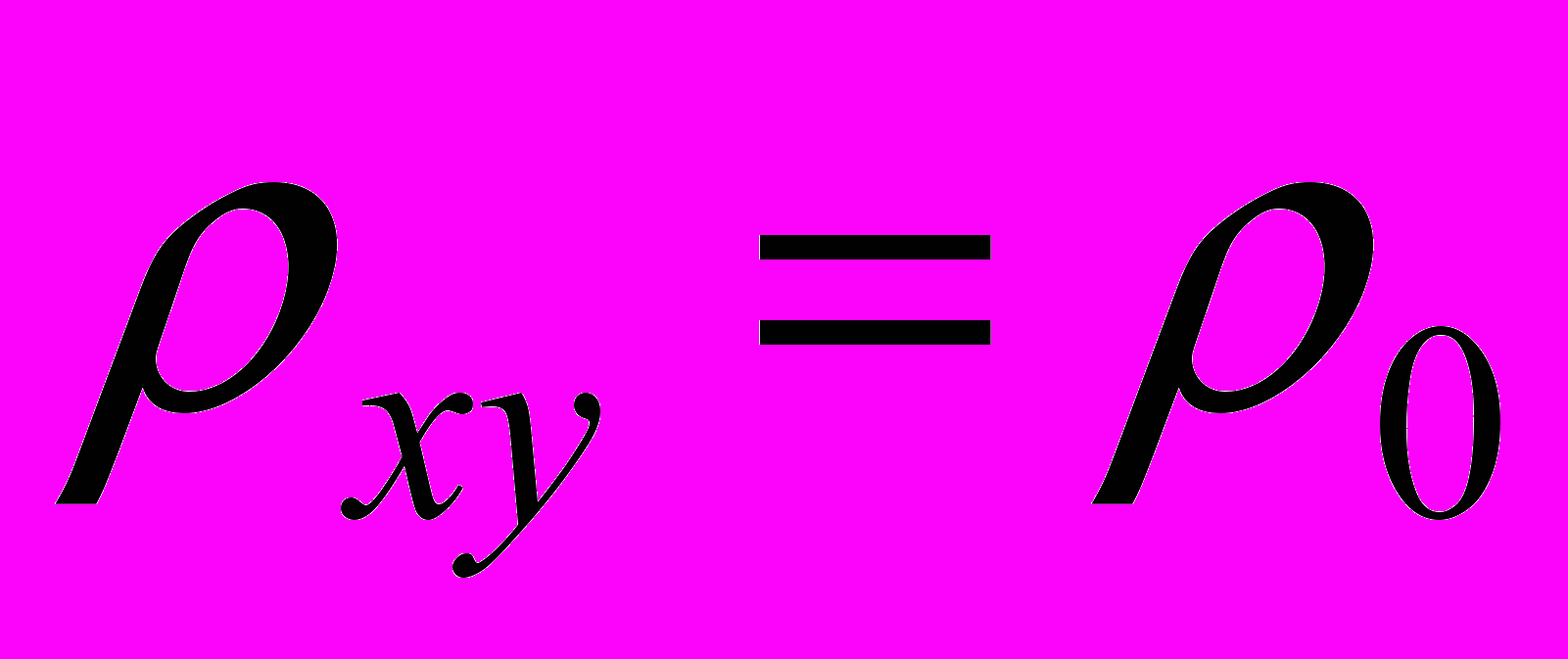H_а: .

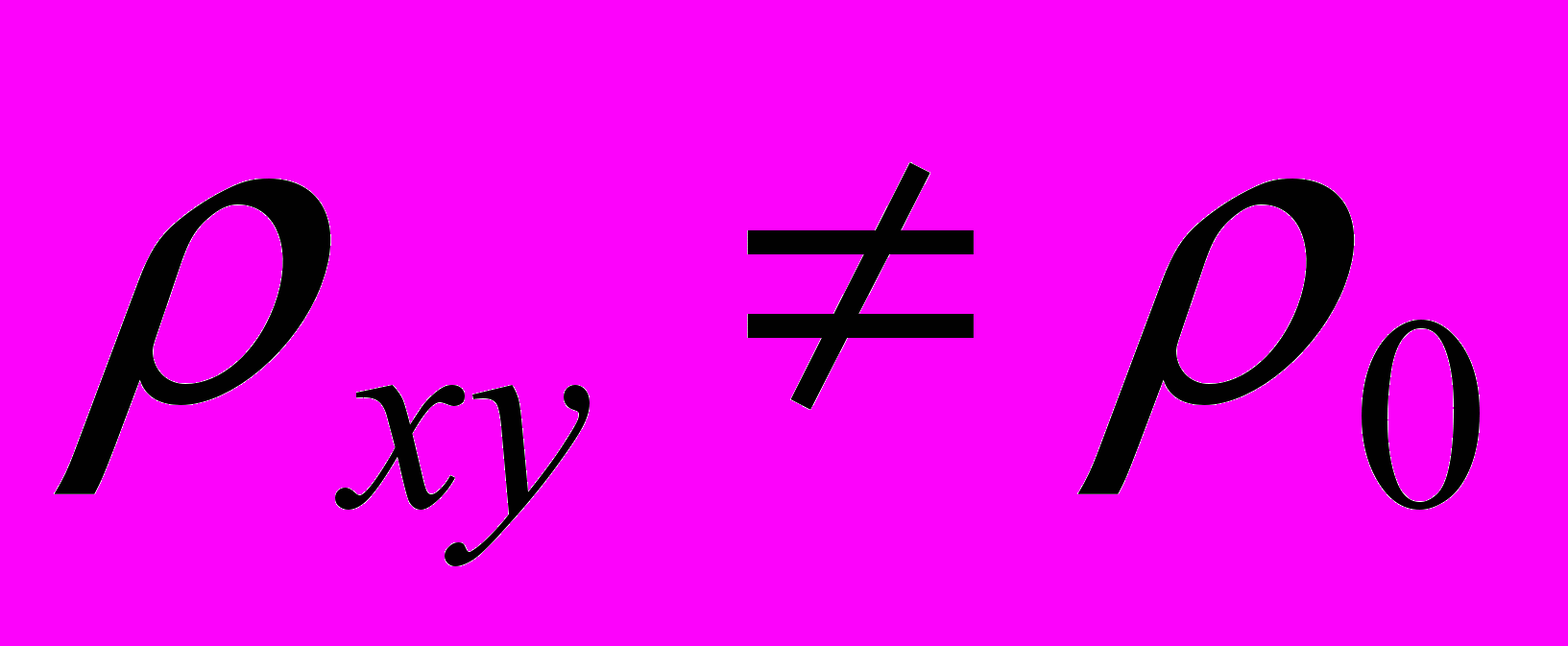Вспомогательную случайную величину вычислим по формуле:

Z* =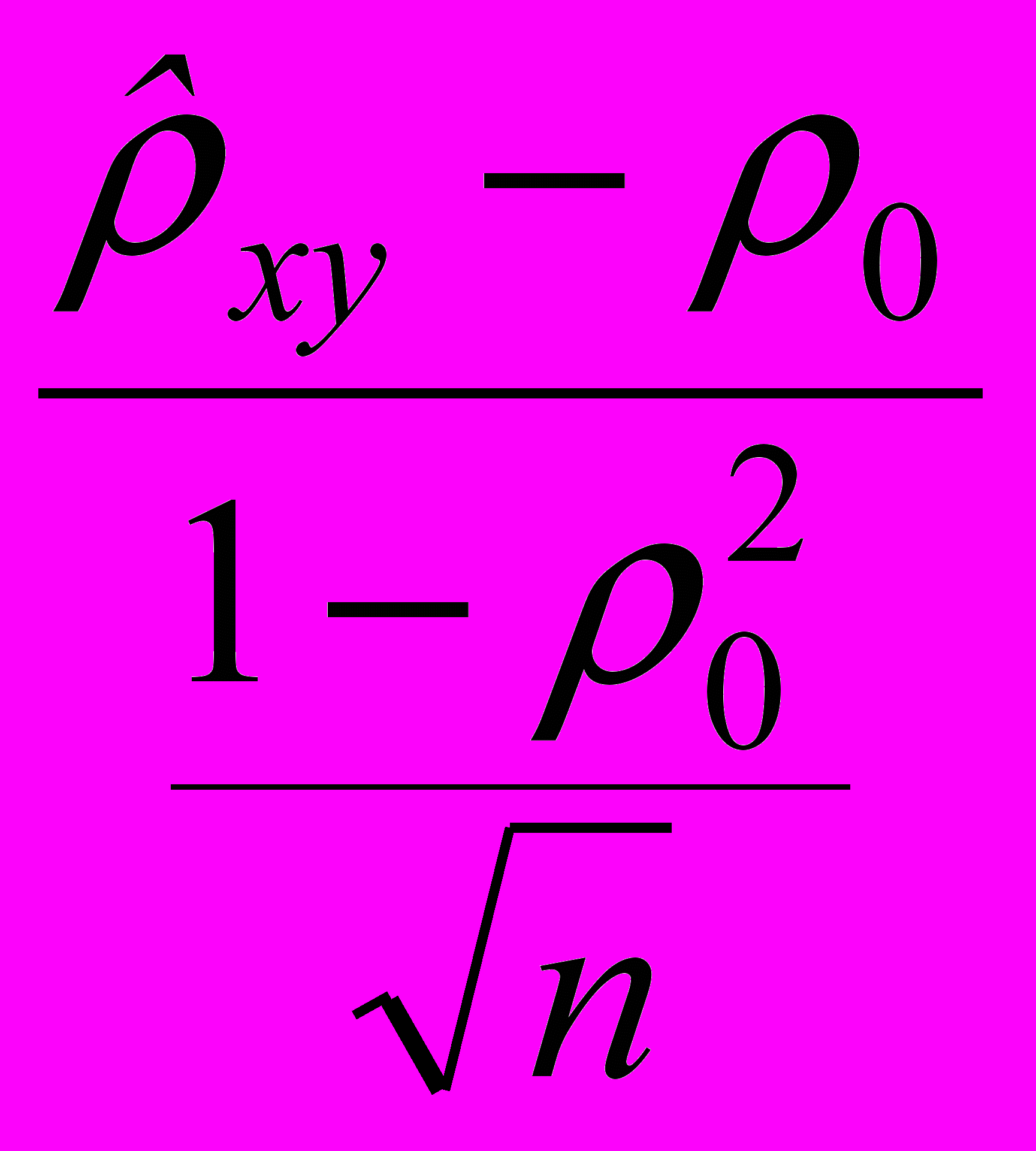. (2.5.2)

Если основная гипотеза верна, то распределение случайной величины Z* асимптотически нормальное с параметрами 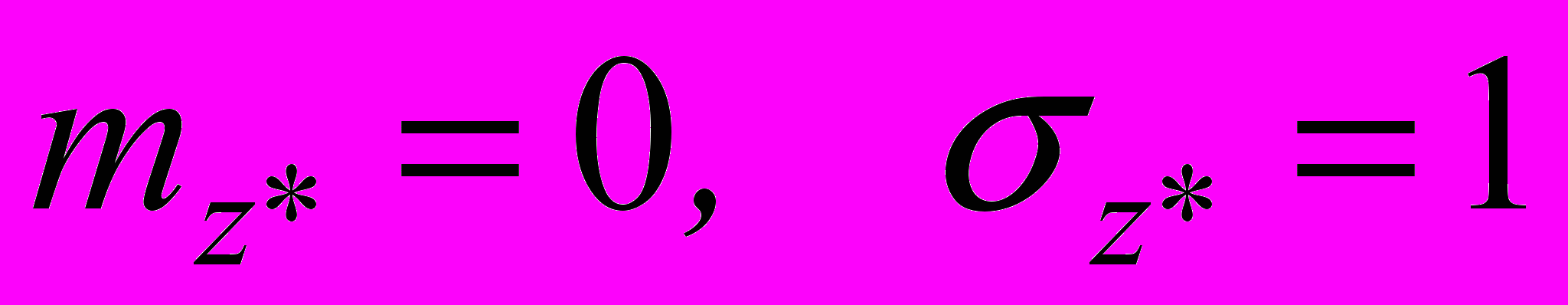. Поэтому границу двусторонней критической области найдем по таблицам Лапласа по заданному уровню значимости (1-) из условия: К₂ =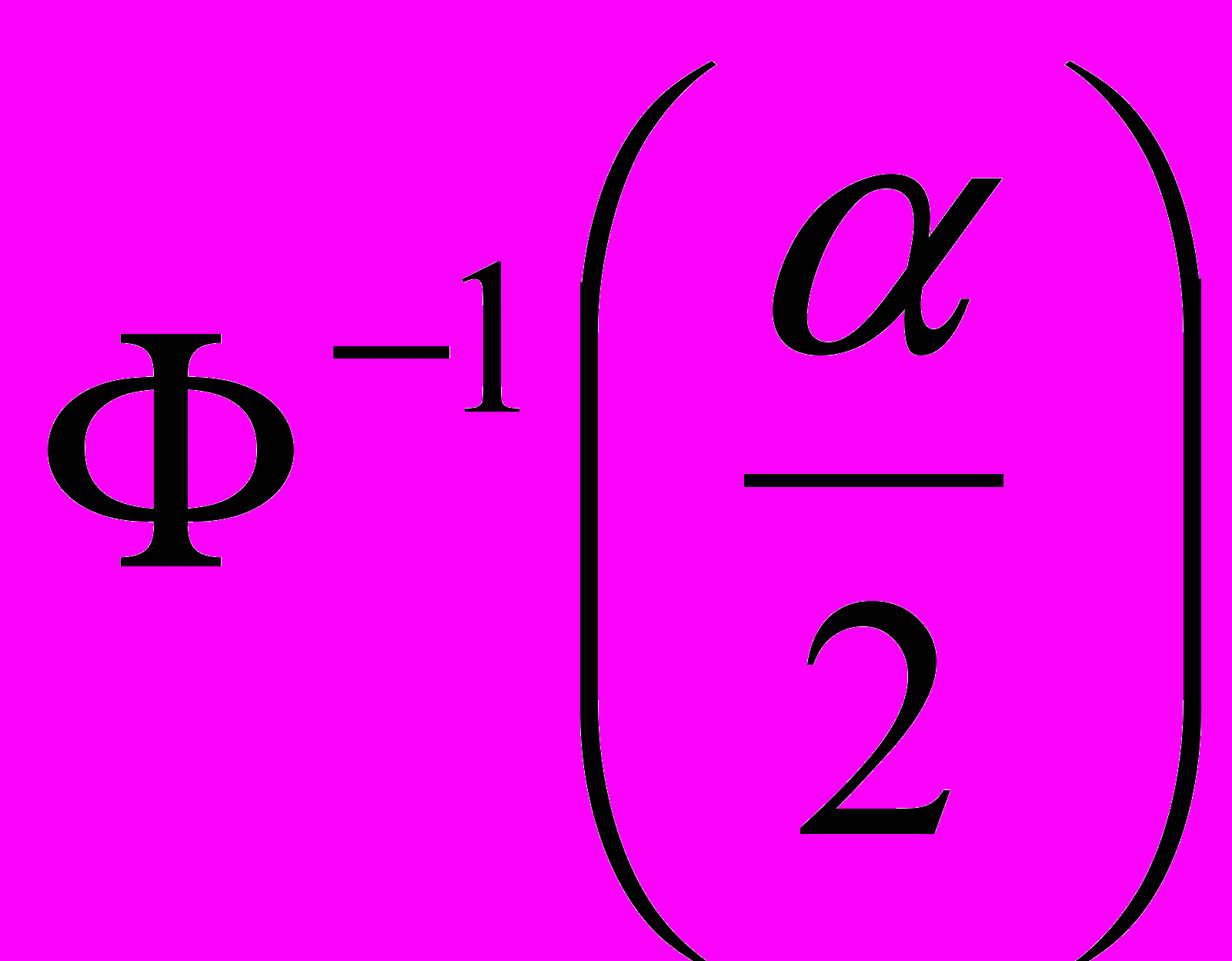, К₁= - К₂. Принимаем основную гипотезу, когда имеет место неравенство: 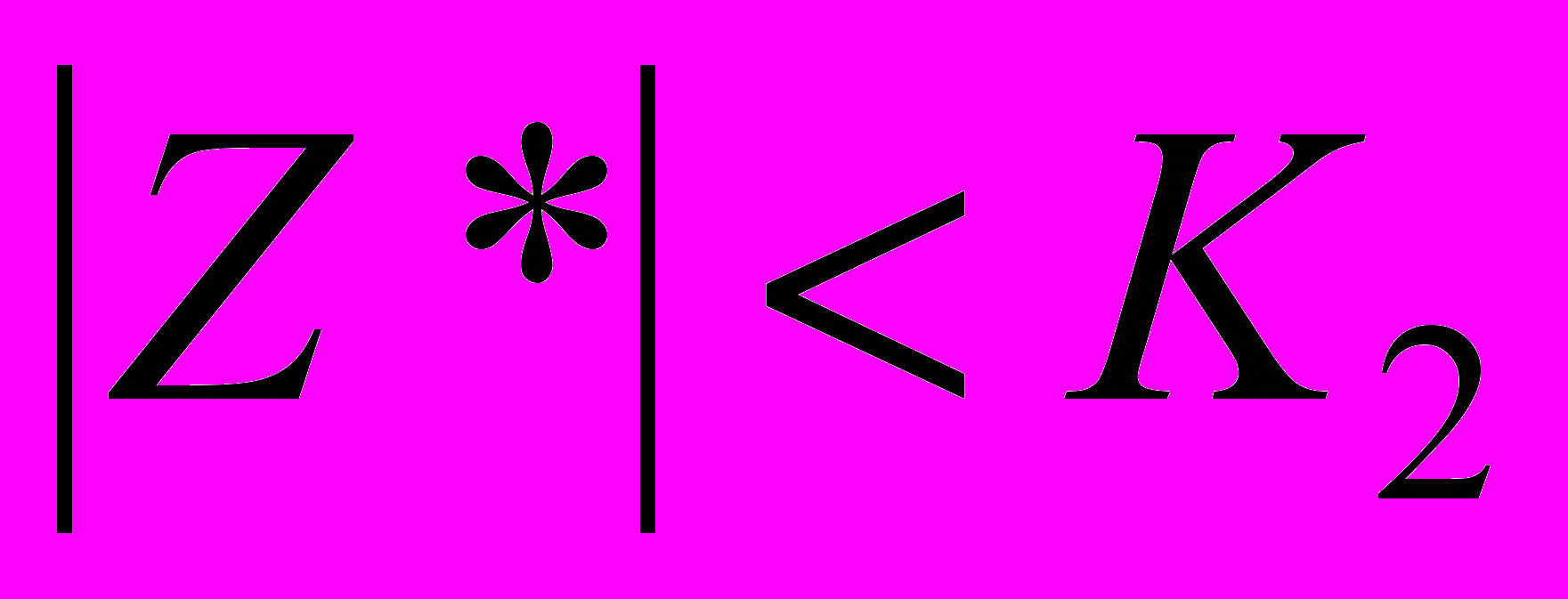, отвергаем основную гипотезу в пользу альтернативной гипотезы, когда выполняется одно из неравенств Z*£ К₁ или Z* ³ К₂.

Если альтернативная гипотеза будет иметь вид H_а: 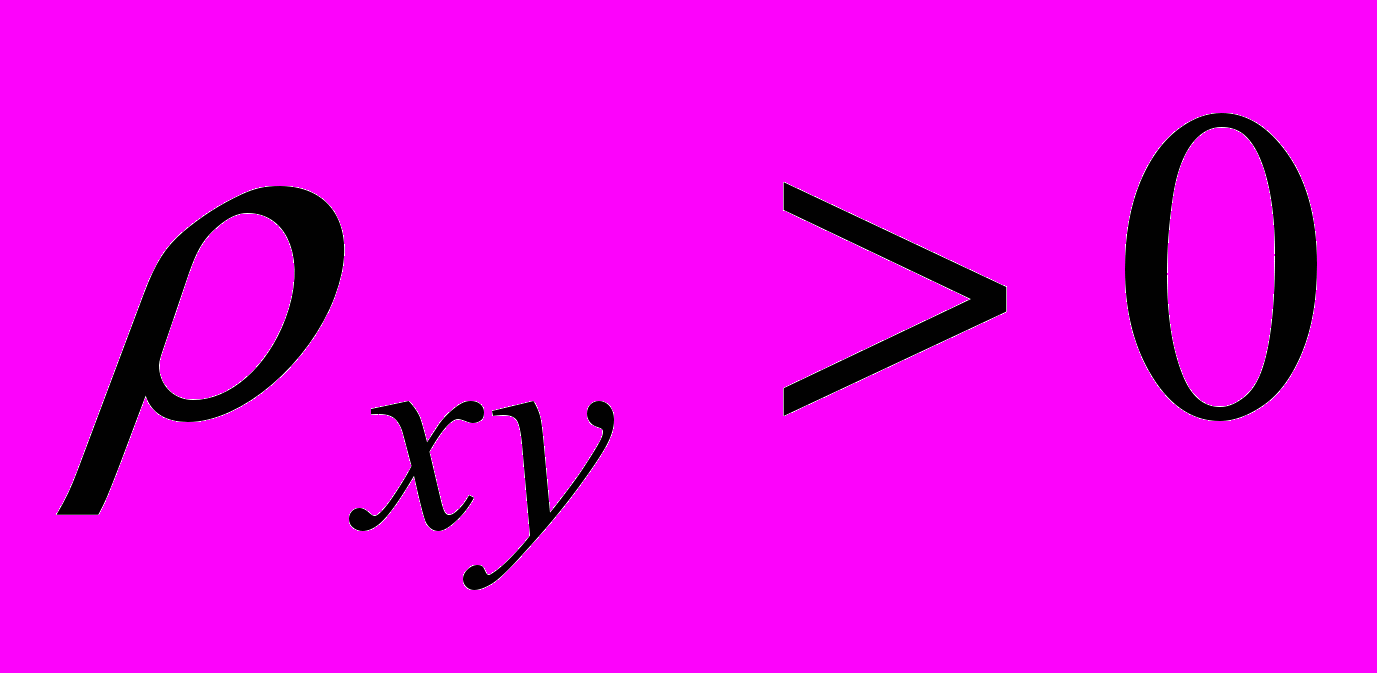или H_а: 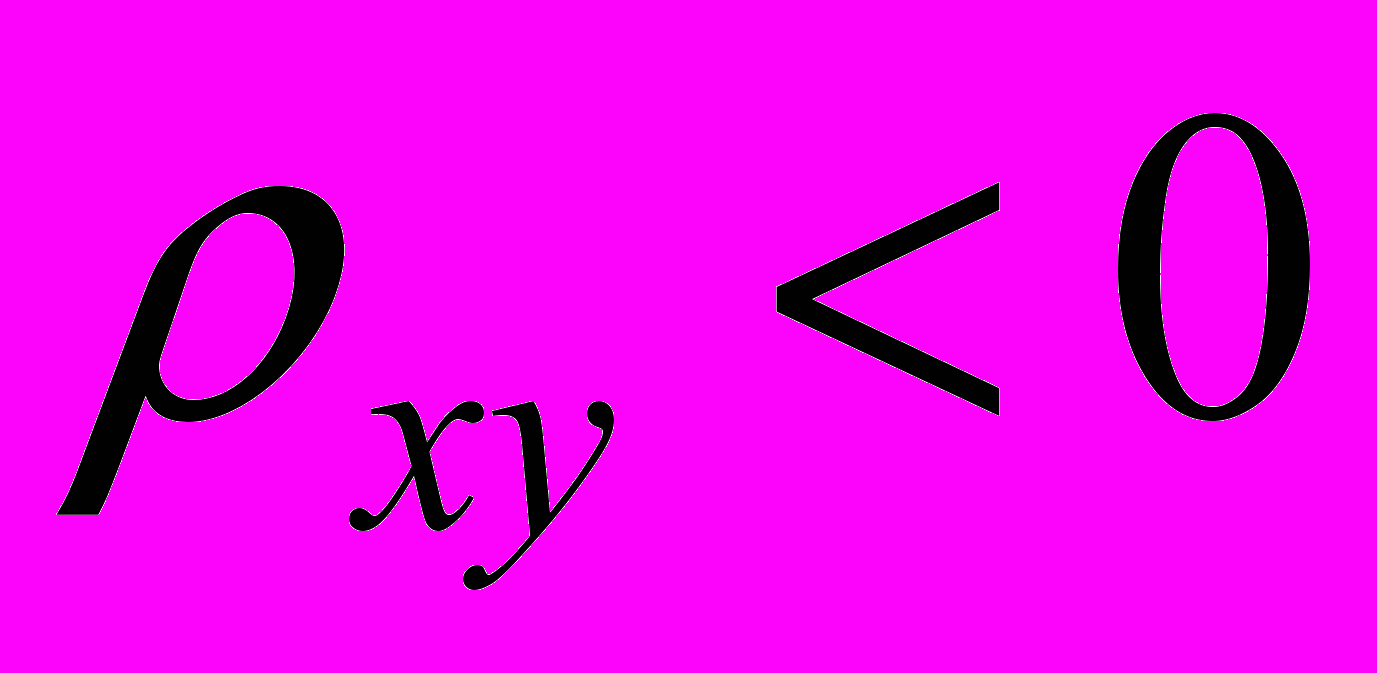, то критическая область будет правосторонней и левосторонней соответственно.

Указанную проверку гипотез рекомендуют проводить при помощи данного критерия, когда 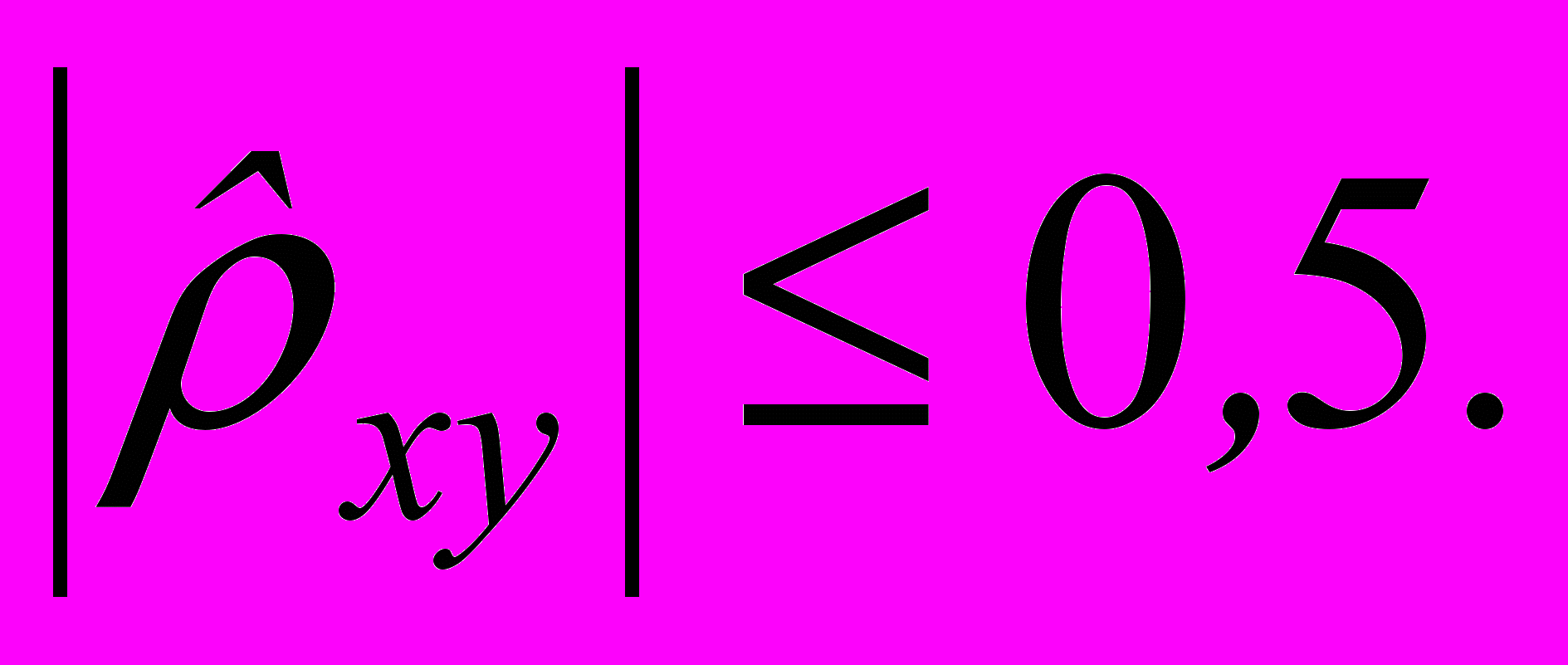Чтобы проверять основную гипотезу без этого ограничения, можно использовать статистику вида (2.5.3):

Z*=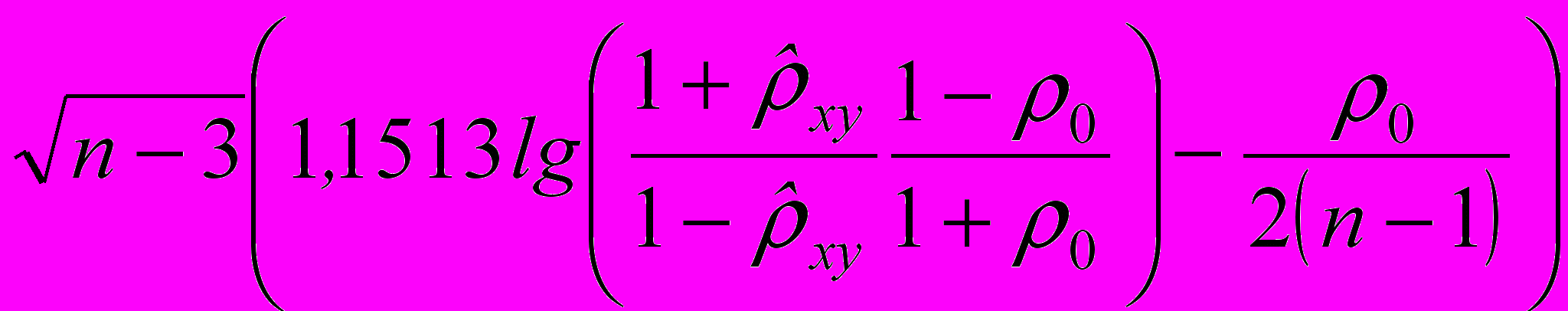. (2.5.3)

Случайная величина (2.5.3) будет также иметь асимптотически нормальное распределение с нулевым математическим ожиданием и единичной дисперсией. Схема принятия или отклонения основной гипотезы полностью повторяет выше изложенную. ▲

^ Для дальнейших рассуждений нам понадобятся следующие понятия: оценка неизвестной дисперсии s², оценка дисперсии для в₁ и для в₀

Несмещенная оценка дисперсии s² будет вычисляться по формуле:

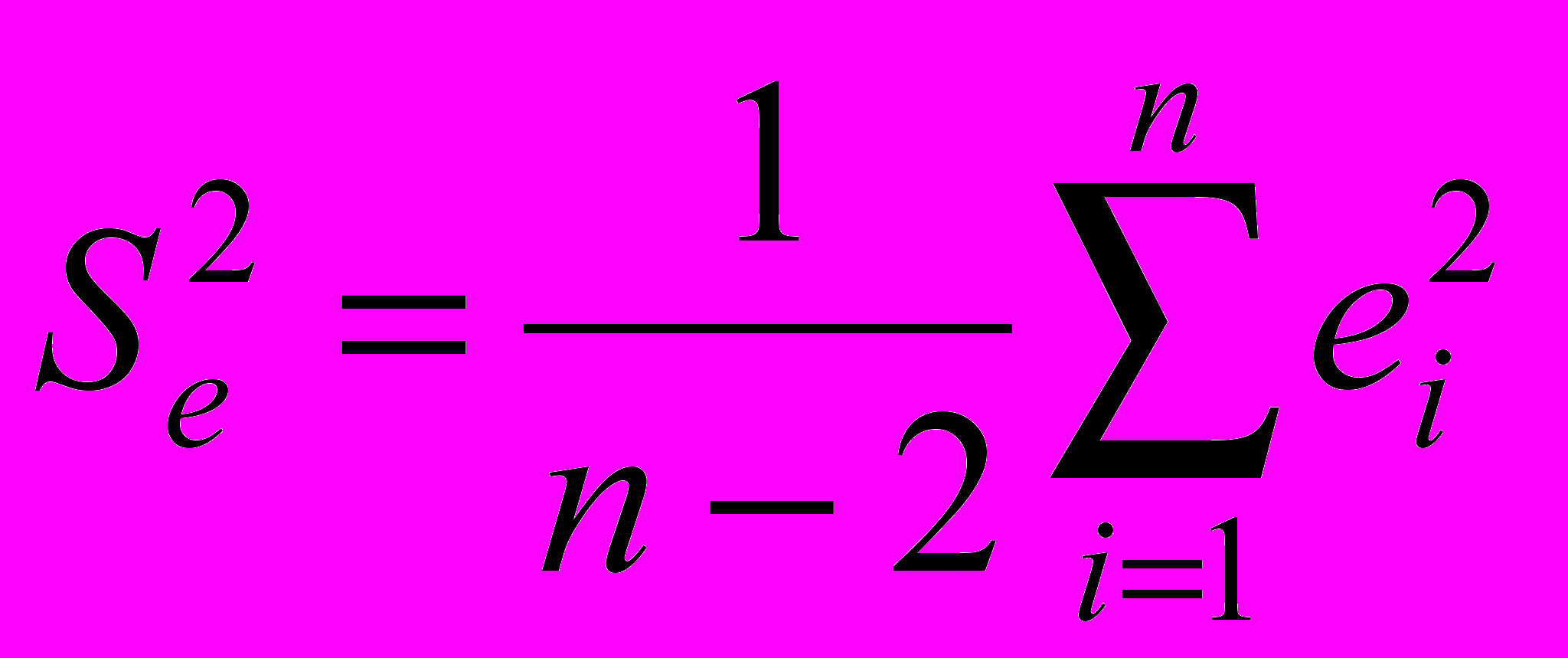. (2.5.4)

Величину



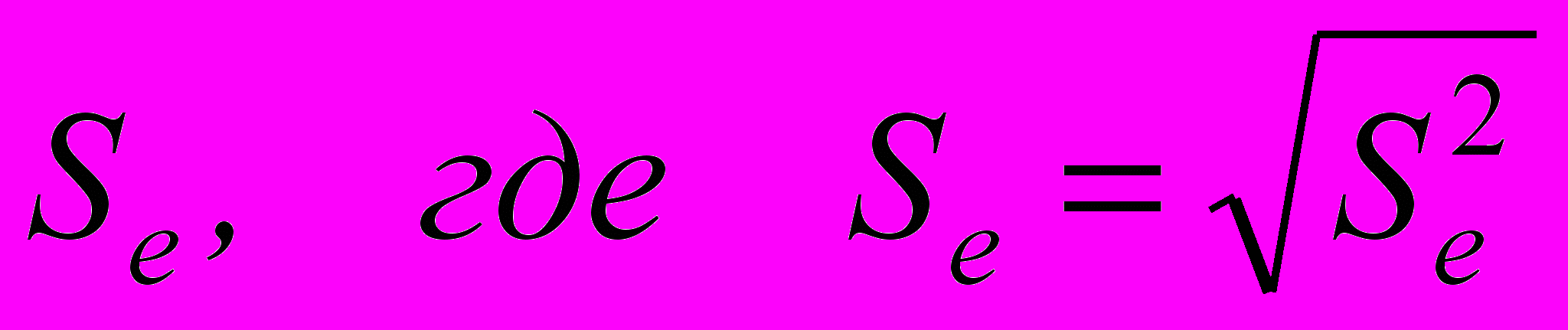
называют стандартной ошибкой.

Таким образом, неизвестные параметры функции линейной регрессии мы оценили при помощи МНК, а неизвестную дисперсию ошибок модели мы оценили по формуле (2.5.4). Как уже отмечалось, найденные оценки параметров в₁ и в₀ являются случайными величинами. Свойства этих оценок мы обсудим в следующем параграфе, здесь приведем только выражение для оценки дисперсии в₁

:

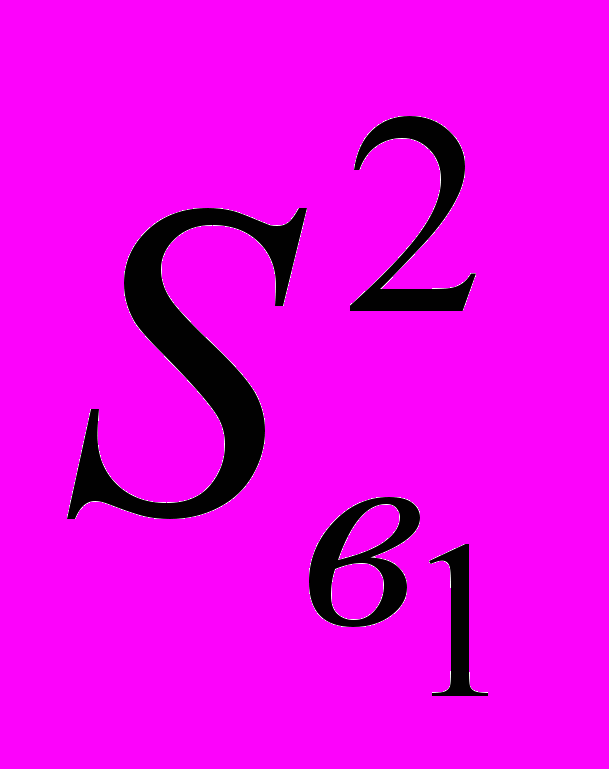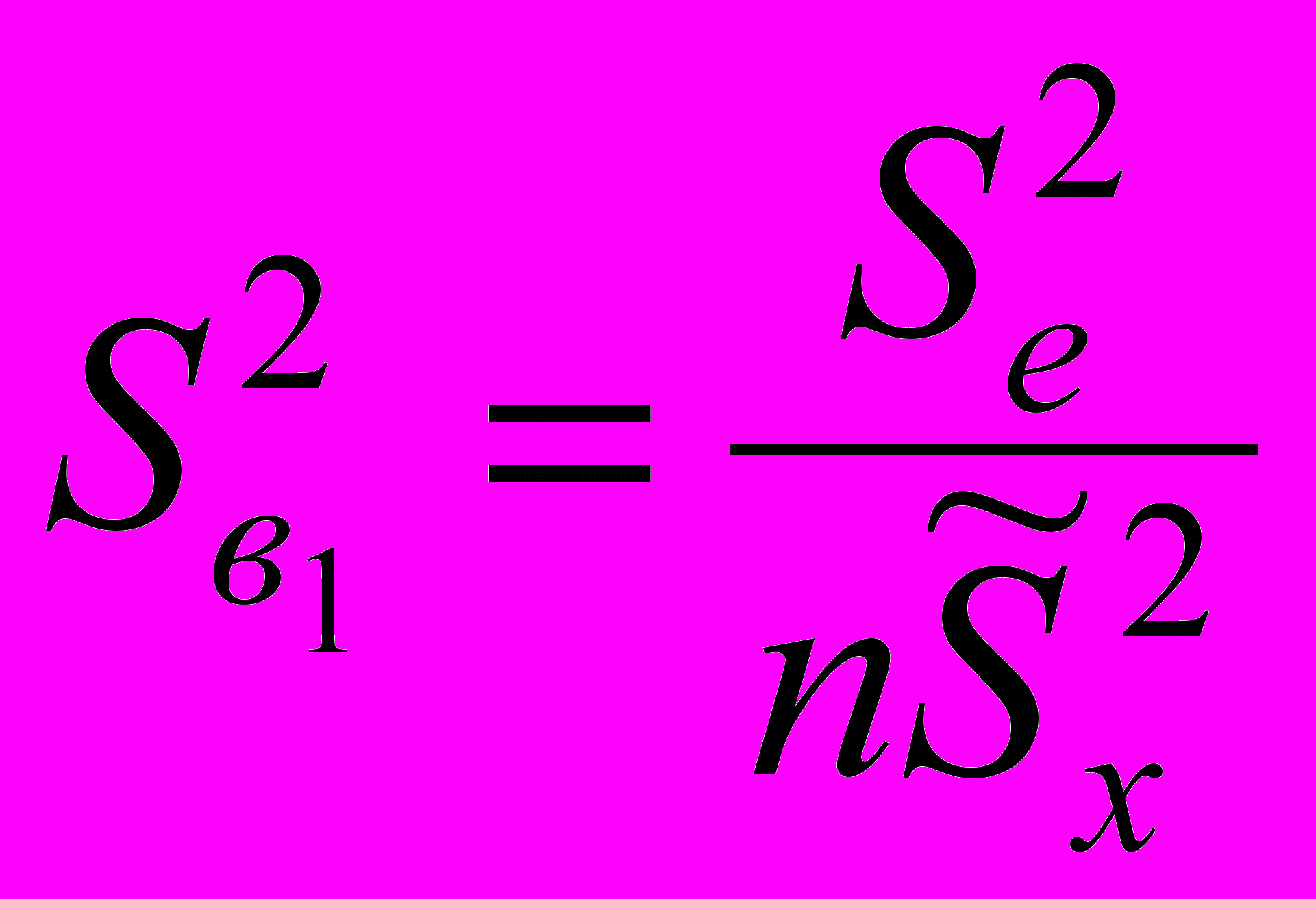. (2.5.5)

Стандартная ошибка оценки в₁ будет равна: .

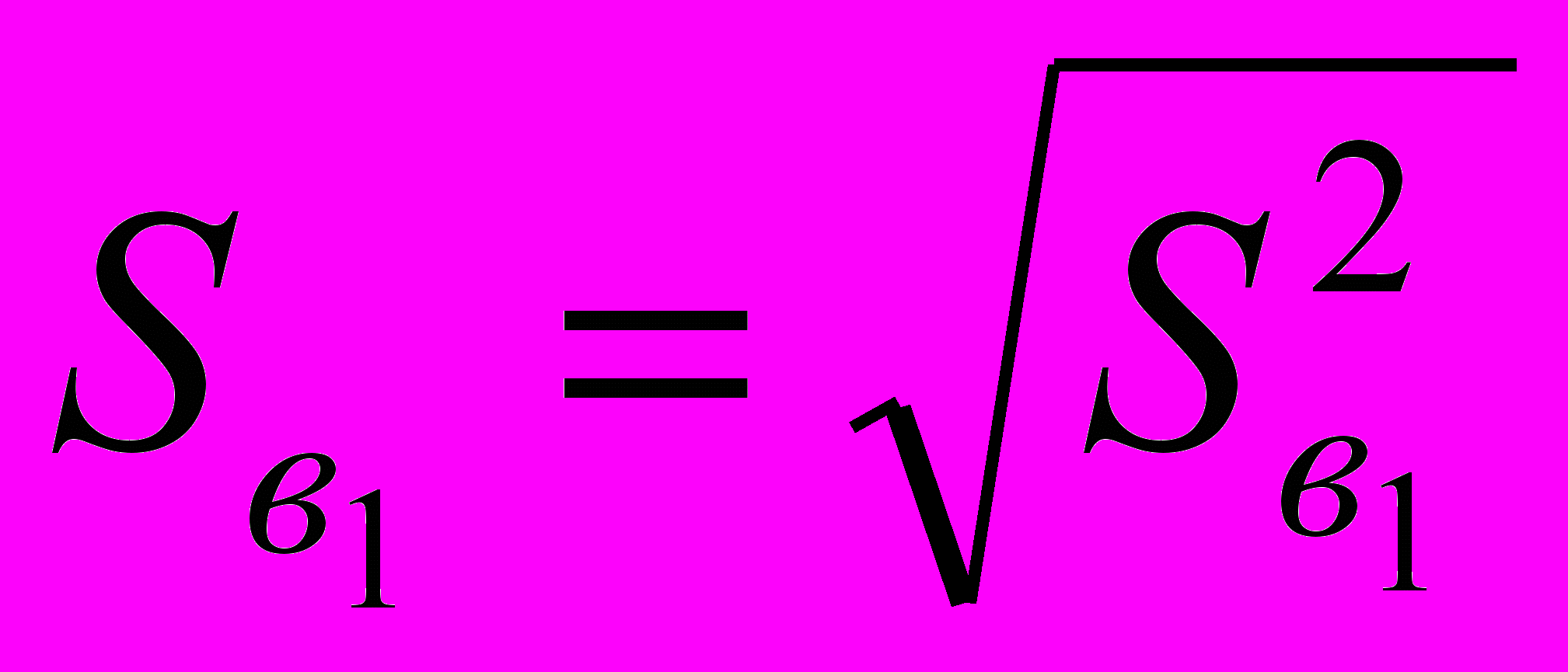Теперь перейдем к рассмотрению статистической проверке гипотезы о линейности функции регрессии. Согласно выбранной модели зависимость переменных х и у имеет вид:

.

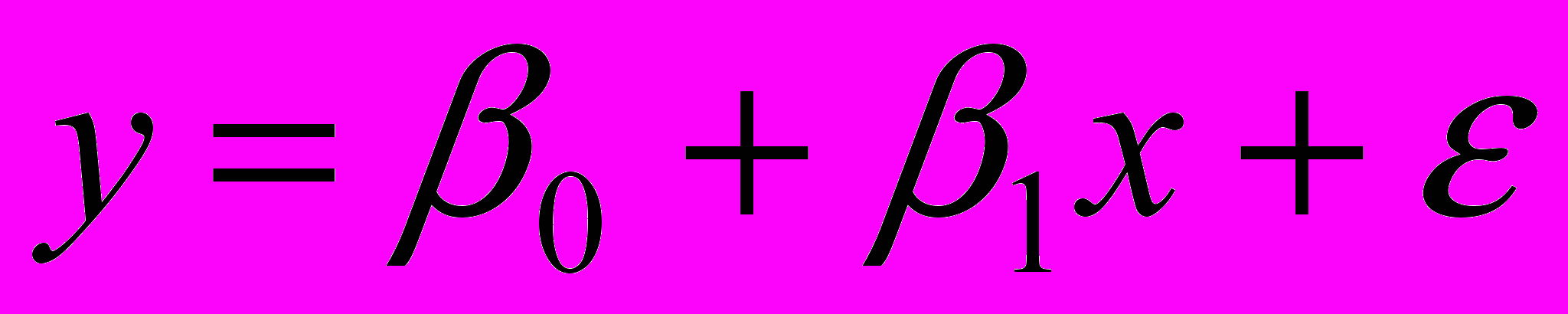Если коэффициент b₁ перед переменной x будет равен нулю, то переменные x и y будут независимы или зависимость y от x будет нелинейной. Поэтому сформулируем основную гипотезу следующим образом:

H₀:

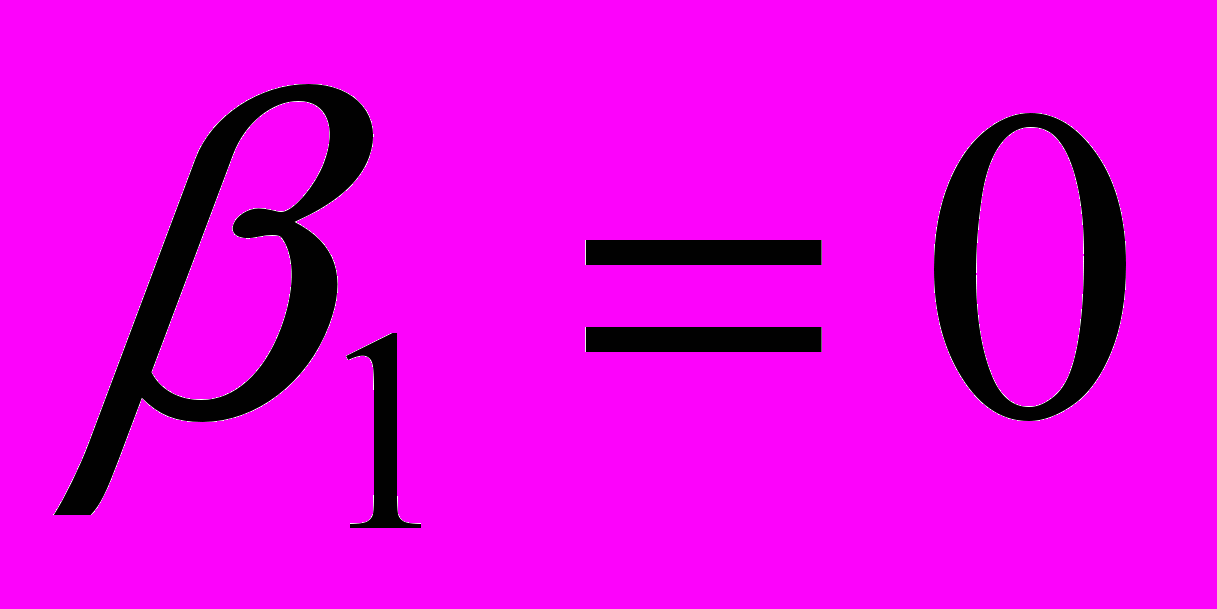
и альтернативную гипотезу H_а:

H_а: .


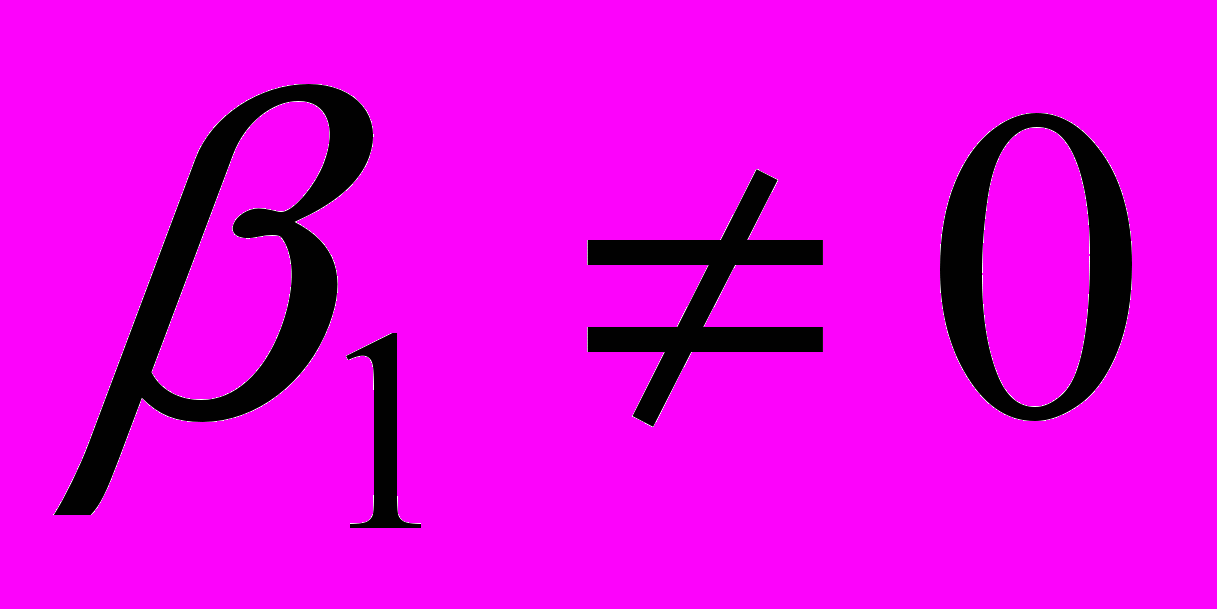Рассмотрим вспомогательную случайную величину вида:


Z*=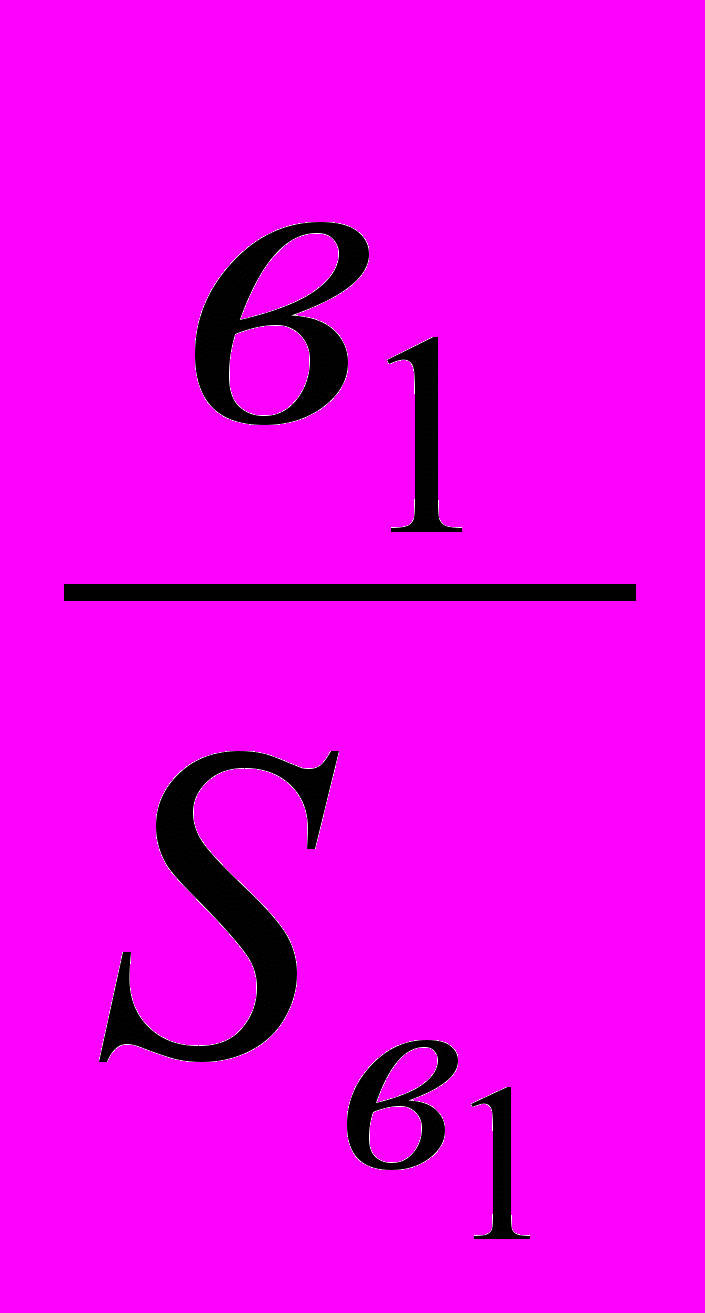. (2.5.6)

Если основная гипотеза верна, то случайная величина (2.5.6) будет распределена по закону Стьюдента с (n-2) степенями свободы. По таблицам распределения Стьюдента, по заданному уровню значимости и (n-2) степеням свободы, находим границу двусторонней критической области К₂, К₁= - К₂. Если выполняется одно из неравенств Z*£ К₁ или Z* ³ К₂, основную гипотезу отвергаем, принимаем альтернативную. В этом случае говорим, что у нас есть основание считать, что предположение о том, что регрессионная модель является линейной, не обосновано. Когда выборочная статистика удовлетворяет неравенству


К₁ < Z* <К₂,

принимаем основную гипотезу и делаем вывод, что у нас нет оснований считать, что у зависит от х линейно, либо делаем вывод, что зависимость может носить нелинейный характер.

^ При альтернативных гипотезах вида: вид H_а: 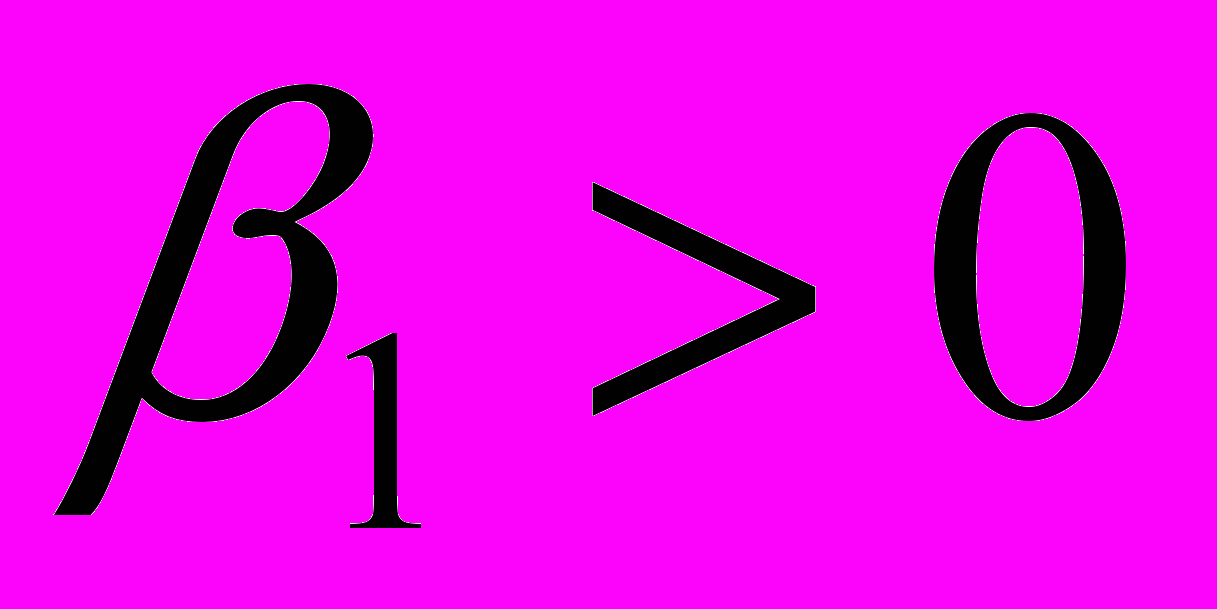или H_а: 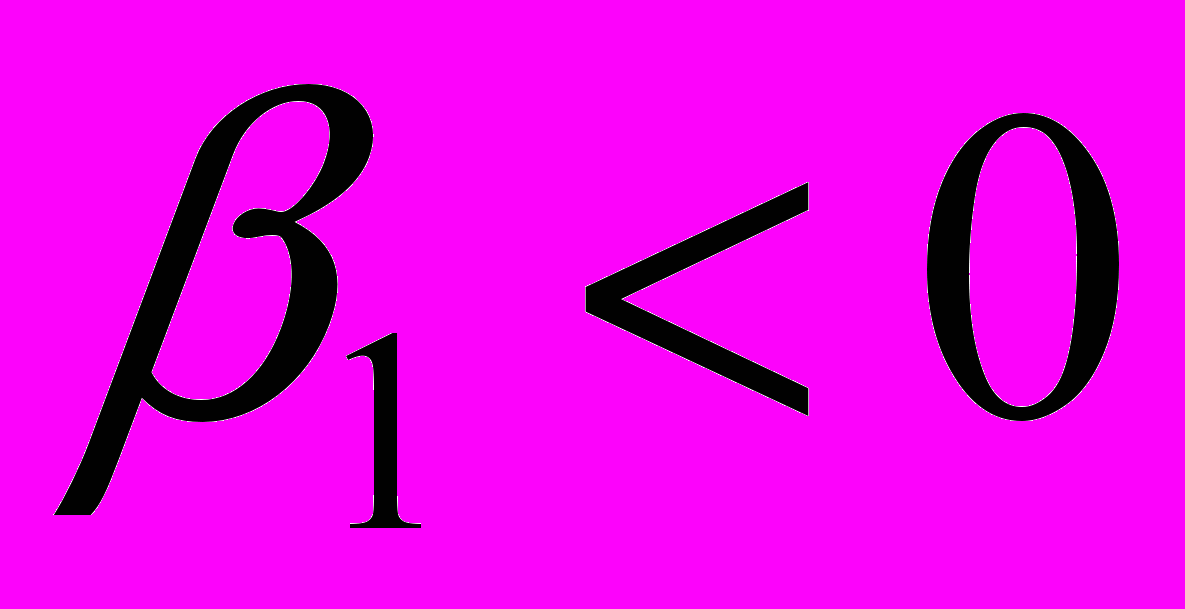, критическая область будет правосторонней и левосторонней соответственно.

Как уже отмечалось, коэффициент детерминации может быть рассмотрен как один из показателей качества модели парной линейной регрессии. Поэтому для проверки адекватности модели парной линейной регрессии эмпирическим данным можно проверить гипотезу о равенстве нулю теоретического коэффициента детерминации:


H₀: ,

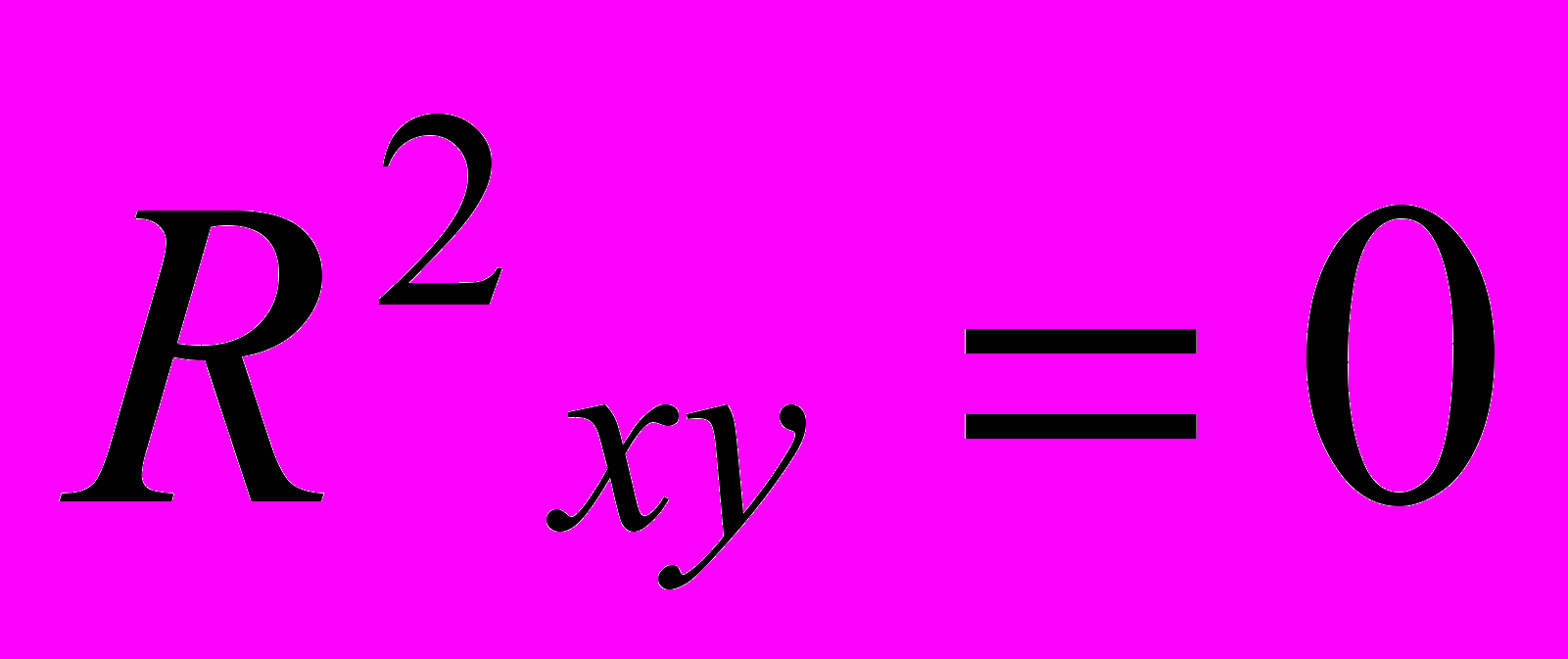H_а: .


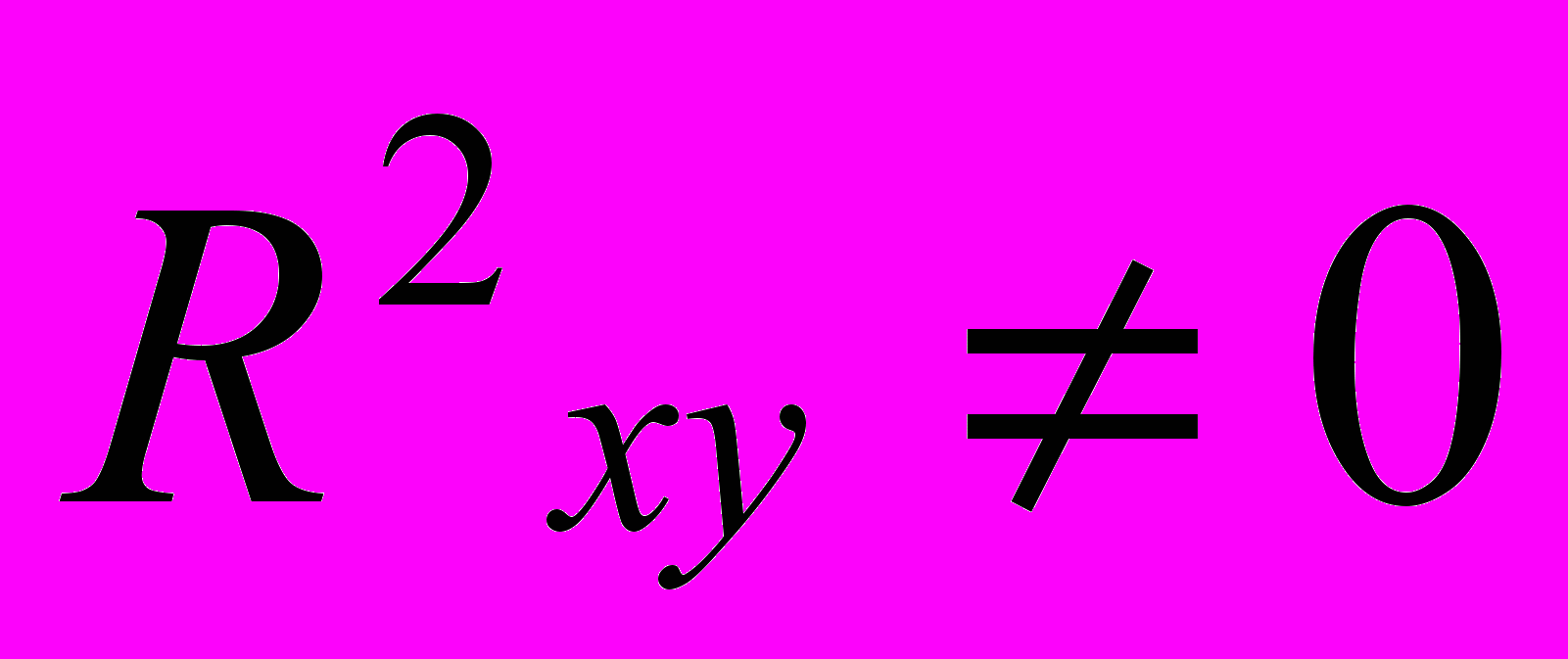Используя выборочный коэффициент детерминации 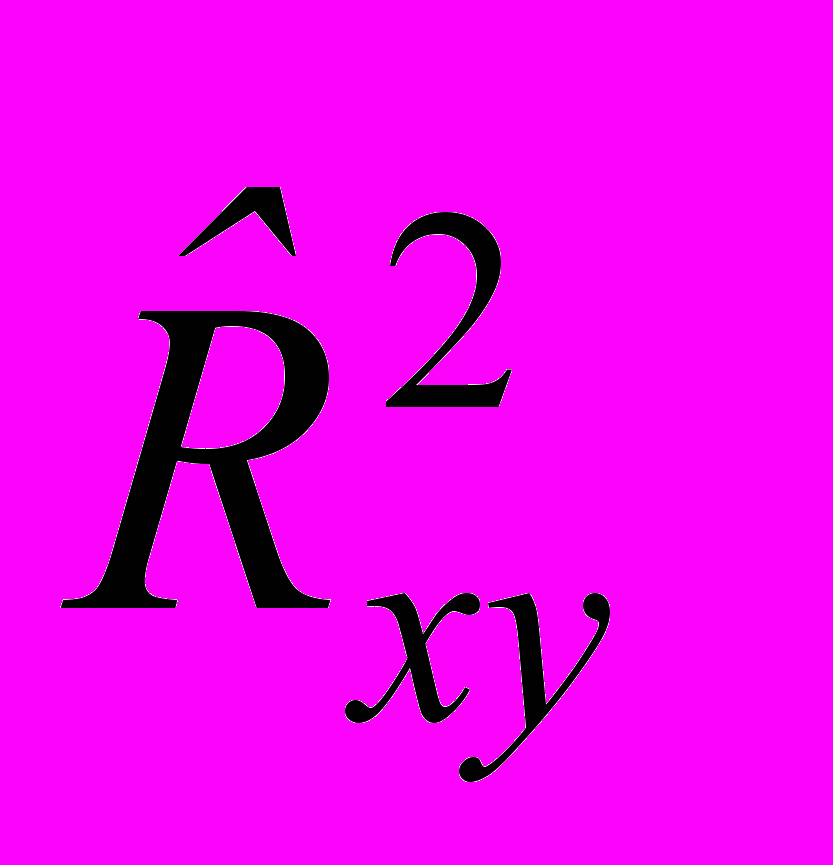, вычисляем выборочную статистику Z* вида:


Z* = 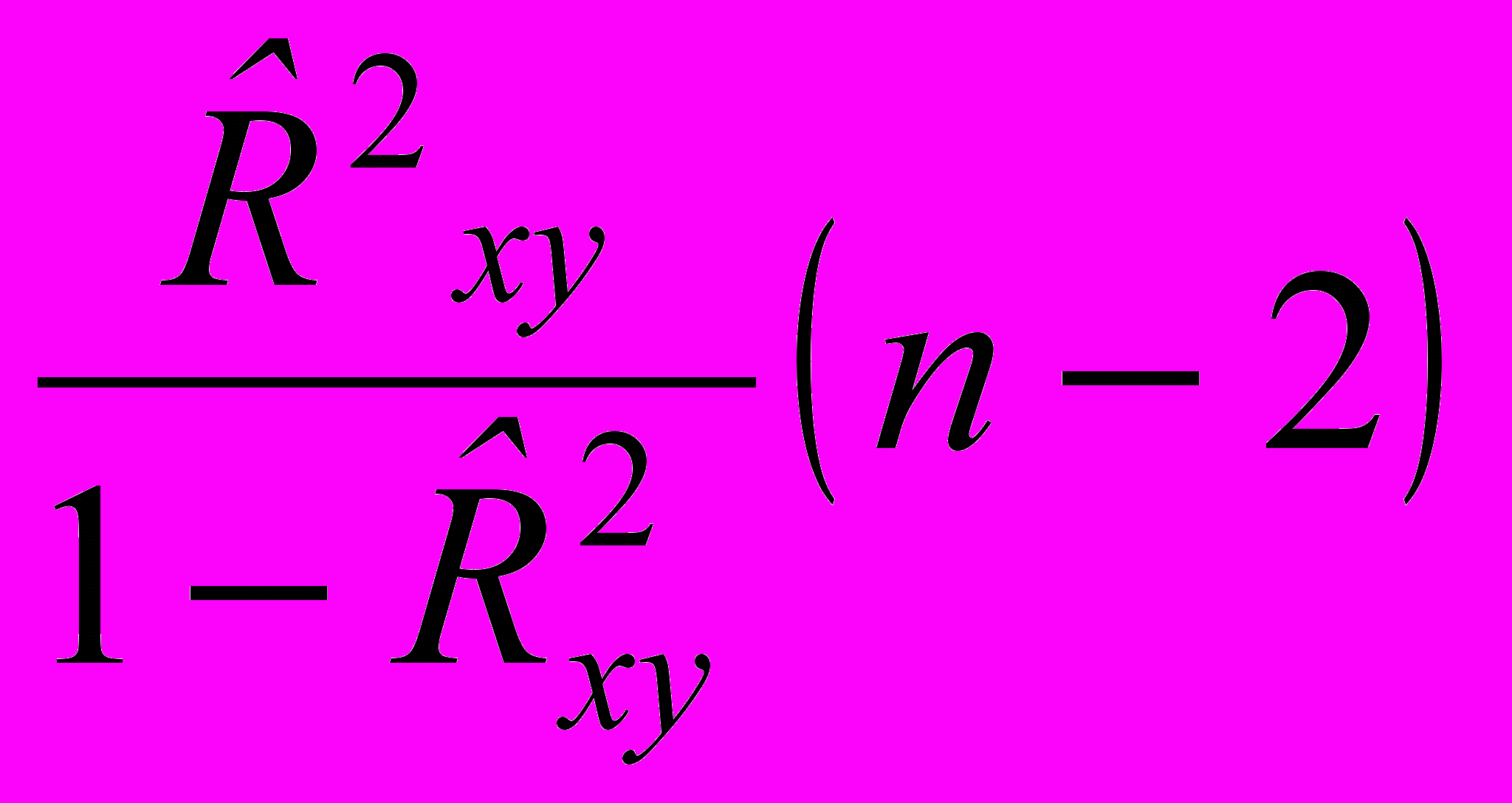. (2.5.7)

Если основное предположение о равенстве нулю коэффициента детерминации верно и изменение у никак не связано с изменчивостью функции регрессии у от х, то случайная величина (2.5.7) будет распределена по закону Фишера с n₁= 1, n₂=(n-2) степенями свободы (ее называют F-статистикой).

Несмотря на вид сформулированной альтернативной гипотезы, критическая область будет правосторонней. Границу критической области ищут по уровню значимости (1-a) и n₁= 1, n₂= (n-2) степеням свободы.

Если 0£ Z*₂, то гипотеза H₀ принимается (делается вывод о том, что либо у и х независимы, либо о том, что линейная связь между ними отсутствует).

Если Z* ³ K₂, то основная гипотеза отвергается, и мы соглашаемся (наше «согласие» носит вероятностный характер!) с предположением о том, что модель парной линейной регрессии адекватна эмпирическим данным.

Замечание 3. При проведении проверки гипотез для нахождения границ критической области в EXCEL можно воспользоваться встроенными функциями категории «Статистические». В том случае, когда выборочная статистика распределена по закону Стьюдента и критическая область двусторонняя, чтобы найти значение К₂, нужно обратиться к функции «СТЬЮДРАСПОБР». Эта функция возвращает искомое значение К₂ по двум входным параметрам: указанной вероятности и известному числу степеней свободы. Например, пусть 1-α =0,05, объем выборки n=50, тогда число степеней свободы (n-2) =48. Значение К₂, используемое при проверке гипотезы будет равно:

К₂ = СТЬЮДРАСПОБР(0,05; 48)= 2,010635.

Поиск границы критической области при проверке гипотезы по критерию Фишера предполагает использование функции «FРАСПОБР». Для того, чтобы найти К₂ – границу правосторонней критической области, при работе с этой функцией нужно ввести три параметра, например

К₂ = FРАСПОБР(0,05; 1;48)= 4,042652.▲