Geum.ru

Изучение теоретической механики

Вид материалаЛекция

Содержание


Лекция 15, 16.
2. Практические занятия
Курсовая работа
Подобный материал:
КАФЕДРА ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ

Московского государственного университета

инженерной экологии


ИЗУЧЕНИЕ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ


Методические указания


Составители Александрова С.Г., Аверьянова Г.М.


МОСКВА – 2003

1. ЛЕКЦИОННЫЕ ЗАНЯТИЯ


Лекция является одним из основных источников знаний, так как она содержит информацию в обобщенном и законченном виде, и в этом заключается ее важное познавательное значение, поэтому изучению лекций студент должен уделять особое внимание. Прежде всего, необходимо обязательное посещение лекций и тщательное их конспектирование. Внимательное прослушивание лекции обеспечивает понимание изучаемого теоретического материала. Для закрепления усвоения прочитанного материала студент должен в этот же день дома просмотреть материал лекции, если есть неясные моменты, то посмотреть соответствующий материал в учебнике. Перед следующей лекцией по курсу студенту следует просмотреть конспект предыдущей лекции совместно с соответствующими параграфами учебника. При регулярной подготовке к лекциям и повторении теоретического материала студенту потребуется на подготовку к каждой лекции около 20 минут.

При изучении раздела «Статика» наиболее трудными темами могут оказаться вопросы приведения плоской и пространственной системы сил к простейшему виду, на них следует обратить особое внимание, надо проследить связь теории, излагаемой при изучении плоской статики, с теорией пространственной статики, почувствовать аналогию (см. Л.1, гл. 3, 4, с. 26-46).

При изучении курса «Кинематика» студенты сталкиваются с несколько большими трудностями. При изучении способов задания движения точки, следует четко усвоить методы определения скорости и ускорения при различных способах задания, особенно разложение ускорения по осям естественного трехгранника.

Необходимо четко представлять вывод формул касательного и нормального ускорения точки (см. Л1, раздел II, гл. 1, с.107-116).

При знакомстве с кинематикой твердого тела особое внимание следует обратить на плоскопараллельное движение твердого тела (Л1, с. 138-167), так как это движение находит широкое применение в технике. С изучением движения плоских механизмов студенты еще столкнутся в курсе прикладной механики. Студенту следует четко усвоить, что существует три подхода к изучению плоского движения тела:
  1. плоское движение представляется как сумма двух движений – поступательного вместе с полюсом и вращения вокруг полюса (теорема 1);
  2. как простое вращение вокруг оси, проходящей через центр мгновенного вращения (теорема Шаля);
  3. как качение без скольжения подвижной центроиды по неподвижной (теорема 3).

При изучении сложного движения точки необходимо усвоить аналитическое доказательство теоремы о сложении скоростей и ускорений (теоремы Кориолиса) (Л1, с. 186-196), понять физические причины появления ускорения Кориолиса, уметь определять его величину и направление.

Раздел «Динамика» является основным в курсе теоретической механики, требует особого внимания, так как подавляющее число конкретных механических задач, которые в наши дни приходится решать любому инженеру, относятся к динамике. Именно в динамике будущий специалист знакомится с основными идеями и методами механики, постигает сущность этой науки и ее роль в изучении и познании окружающего нас мира.

Изучение курса динамики начинается с основных законов динамики, затем изучается динамика точки, при этом студенту следует усвоить преимущества инерциальных систем отсчета, уметь записывать основное уравнение динамики в инерциальной и неинерциальной системах (Л1, с. 223-252).

Общие теоремы динамики находят особенно широкое применение при решении задач, поэтому их надо очень четко знать (Л1, с. 281-339).

При изучении принципов механики студенту следует усвоить, что принцип возможных перемещений дает общий метод решения задач статики, а принцип Даламбера позволяет использовать для решения динамических задач уже известные методы статики (Л1, с. 348-381).

Уравнения Лагранжа II-го рода дают общий метод решения задач динамики. Студент должен четко представлять, что такое обобщенные координаты и обобщенная сила, преимущества уравнений Лагранжа (Л1, с. 381-402).

Большое место при изучении динамики отводится теории малых колебаний систем с одной степенью свободы. Студент должен понять вывод дифференциальных уравнений малых колебаний, а затем уже рассмотреть различные виды колебаний (Л1, с. 407-472).


Календарный план лекций для студентов специальностей

171200, 170500, 220300,101700.


Дисциплина: «Теоретическая механика»

Второй семестр

Статика.

Лекция 1. Введение. Основные понятия статики. Аксиомы статики. Виды связей и их реакции (Л1, с. 4-13)

При прослушивании этой лекции студент обязательно должен усвоить основные понятия статики и четко знать виды связей и их реакции, так как все задачи статики посвящены определению этих неизвестных реакций связей.

Лекция 2. Понятие момента силы. Алгебраический момент силы относительно точки. Векторный момент силы относительно центра. Момент силы относительно оси. Связь момента силы относительно оси и вектора момента силы относительно точки.

Понятие пары сил. Алгебраический момент пары сил. Момент пары как вектор. Некоторые теоремы о парах сил. (Л1, с. 20-25 и с. 28-38).

При прослушивании этой лекции студент должен четко усвоить, что вращательное действие силы характеризуется ее моментом, знать, как берется момент силы относительно центра и оси.

Важной мерой механического действия силы является пара сил. Студент должен ясно представлять, что действие пары сил на тело характеризуется ее моментом, понимать, как берется момент пары сил.

Лекция 3. Приведение произвольной пространственной системы сил к простейшему виду. Главный вектор системы сил и главный момент системы сил относительно центра приведения. Аналитические зависимости для вычисления главного вектора и главного момента системы. Условия и уравнения равновесия произвольной плоской системы сил, различные формы уравнений равновесия плоской системы сил (Л1, с. 38-46, с.49-51).


Кинематика.

Лекция 4. Введение в кинематику. Кинематика точки. Способы задания движения точки. Определение скорости и ускорения точки при векторном и координатном способах движения точки (Л1, с.97-107).

Лекция 5. Естественный трехгранник, естественные оси. Некоторые сведения из дифференциальной геометрии: определение касательной к кривой, угол смежности, кривизна и радиус кривизны кривой. Определение скорости точки при естественном способе задания движения точки. Разложение ускорения по осям естественного трехгранника. Касательное и нормальное ускорение точки. Частные случаи. (Л1, с. 1070116).

После прослушивания этих лекций студент должен четко усвоить, как определяются основные кинематические характеристики движения точки: ее скорость и ускорение. Уметь определять их величину и направление. Обязательно надо знать, что ускорение точки в общем случае раскладывается на две составляющие – тангенциальное (a τ) и нормальное (a n), a τ – характеризует изменение скорости по величине , a n – по направлению.

Лекция 6. Простейшие движения твердого тела. Поступательное движение твердого тела. Вращение твердого тела вокруг неподвижной оси. Определение, закон вращения. Угловая скорость и угловое ускорение тела, их векторное представление. Определение скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси. (Л1. с. 123 – 134).

Эти темы являются очень важными при изучении кинематики, так как любое движение тела можно представить как сумму двух движений – поступательного и вращательного.

Лекция 7. Сложное движение точки. Определения абсолютного, относительного и переносного движения. Определения относительной, переносной и абсолютной скорости точки. Теорема о сложении скоростей и теорема о сложении ускорений (теорема Кориолиса). Способы определения величины и направления кориолисова ускорения. Физический смысл акор (Л1 стр 134-138, 186-196).

Лекция 8. Плоскопараллельное (плоское) движение твердого тела. Определение, уравнения движения. Разложение движения плоской фигуры на составляющие (первая основная теорема плоского движения). Определение скоростей точек плоской фигуры. Мгновенный центр скоростей, его свойства и способы определения. Определение скоростей точек и угловых скоростей звеньев плоских механизмов с помощью мгновенного центра скоростей. (Л1 стр. 138 – 149).

Лекция 9. Итоговая.


Третий семестр

Динамика

Лекция 1. Введение. Предмет динамики, законы динамики. Динамика точки. Дифференциальные уравнения движения точки в векторной форме и в проекциях на оси координат. Две основные задачи динамики точки. (Л1 стр. 223 – 235).

Лекция 2. Относительное движение материальной точки. Дифференциальные уравнения относительного движения материальной точки. Частные случаи: относительный покой, принцип относительности классической механики. Понятие об инерциальных системах отсчета. (Л1 стр. 249 – 252).

Лекция 3, 4. Динамика механической системы. Масса системы, центр масс. Классификация сил, действующих на систему. Основные свойства внутренних сил. Дифференциальные уравнения движения механической системы. (Л1 стр. 260, 281 – 283). Общие теоремы динамики точки и системы. Теорема о движении центра масс. Следствия из теоремы (Л1 стр. 290 – 294). Понятие количества движения точки. Теорема об изменении количества движения точки. Главный вектор количеств движения механической системы. Теорема об изменении количества движения системы. Следствия из теоремы. (Л1 стр. 283 – 290).

Лекция 5. Геометрия масс. Понятие о моментах инерции твердого тела относительно плоскости, оси и полюса. Связь между ними. Теорема о вычислении моментов инерции тела относительно параллельных осей. Вычисление моментов инерции простейших тел: тонкого однородного стержня, сплошного цилиндра (диска), полого цилиндра. Радиус инерции (Л! стр. 262 – 270).

Лекция 6. Понятие момента количества движения точки относительно центра и осей координат. Теорема об изменении момента количества движения материальной точки. Следствия. Главный момент количества движения точек механической системы (кинетический момент) относительно центра и осей координат. Вычисление кинетического момента твердого тела в различных случаях его движения. Теорема об изменении кинетического момента системы. Следствия из теоремы (Л1 стр. 295 – 311).

Лекция 7. Динамика твердого тела. Дифференциальные уравнения поступательного, вращательного и плоскопараллельного движения тела (Л1 стр. 303, 309 – 310).

Понятие о работе силы. Работа постоянной силы. Элементарная работа. Работа силы на конечном пути. Две теоремы о работе. Примеры вычисления работ некоторых сил: силы тяжести, силы упругости, силы, приложенной к вращающемуся твердому телу (Л1 стр. 311 – 319).

Лекция 8. Понятие кинетической энергии точки и системы. Теорема об изменении кинетической энергии точки и механической системы. Пример (Л1 стр. 311 – 331).

Лекция 9. Силовое поле. Потенциальное силовое поле, силовая функция. Условия существования потенциального силового поля. Работа сил потенциального силового поля. Понятие потенциальной энергии. Связь силовой функции и потенциальной энергии системы. Закон сохранения полной механической энергии. (Л1 стр. 331 – 348).

Лекция 10. Принцип Даламбера для точки и механической системы. Метод кинетостатики. Приведение сил инерции точек твердого тела к центру. Главный вектор и главный момент сил инерции, их вычисление при различных случаях движения тела. (Л1 с. 348 – 358).

Лекция 11. Аналитическая механика. Виды связей. Перемещения возможные и действительные. Идеальные связи. Принцип возможных перемещений (Л1 с. 369 – 378).

Лекция 12. Общее уравнение динамики. (Л1 с. 386 – 387). Понятие об обобщенных координатах. Вычисление возможной работы в обобщенных координатах. Обобщенные силы. Примеры вычисления обобщенных сил (Л1 с. 378 – 383).

Лекция 13. Условия равновесия системы в обобщенных координатах. Случай сил, имеющих потенциал. Связь обобщенной силы и потенциальной энергии системы. Понятие об устойчивости равновесия. Теоремы Ляпунова и Лагранжа – Дирихле (без вывода) (Л1 с. 383 – 386, 396 – 407).

Лекция 14. Дифференциальные уравнения движения механической системы в обобщенных координатах (уравнения Лагранжа II-го рода) (Л1 с. 393 – 402).

Лекция 15, 16. Малые свободные колебания механических систем с одной степенью свободы около положения устойчивого равновесия. Гармонические колебания, амплитуда и период колебаний. Фазовая плоскость, фазовые траектории, фазовый портрет. Свободные затухающие колебания системы. (Л1 с. 413 – 430).

Лекция 17. Обзорная.


2. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ


Основное назначение практических занятий – закрепление знаний, получаемых студентами на лекциях и при работе над учебником, а также приобретение навыков в решении основных типов задач. Эти занятия способствуют налаживанию самостоятельной работы студентов по изучению материала курса.

К каждому семинарскому занятию студент должен готовиться, прочитав теорию по теме занятия, по лекциям или соответствующие разделы учебника. На практических занятиях студент должен с помощью преподавателя научиться использовать теоретические знания в решении конкретных задач механики, при этом необходимо активно участвовать в работе семинара и выполнять домашние задания.

При решении задач статики наибольшие трудности возникают при рассмотрении «Равновесия системы тел» и «Равновесия пространственной системы сил», студенту при изучении этих тем следует пользоваться методическими указаниями по решению задач статики, изданными кафедрой – МУ1 и МУ5.

При решении задач по кинематике основные трудности возникают при рассмотрении «Плоского движения тела», «Сложного движения точки». Студент должен овладеть основными формулами кинематики, уметь вычислить скорости и ускорения и грамотно изобразить их на чертеже. При решении задач на эти темы следует пользоваться методическими указаниями МУ2 и МУ4 и учебником (Л1 стр. 139 – 156 и 186 – 191).

При решении задач по динамике студент должен четко представлять, что раздел «Динамика» является основным в курсе теоретической механики, требует особого внимания, так как подавляющее число конкретных механических задач, которые в наше время приходится решать инженеру, относится к динамике. Именно в динамике будущий специалист знакомится с основными идеями и методами механики, постигает сущность этой науки и ее роль в изучении и познании окружающего нас мира.


Календарный план практических занятий со студентами специальностей

171200, 170500, 220300,101700.

Второй семестр

Статика

Занятие 1. Плоская статика. Виды связей и их реакции. Классификация сил, действующих на систему. Уравнения равновесия произвольной плоской системы сил. (В аудитории решаются задачи 4.7; 4.14; 4.26, на дом – 4.15; 4.22)*.

На первом занятии студент должен четко усвоить виды связей и их реакции. Записать и усвоить план решения любой задачи по статике. Научиться составлять уравнения равновесия плоской системы сил. Еще студент должен понять, что распределенную нагрузку, действующую на тело, необходимо заменить сосредоточенной силой, и научиться это делать для различных нагрузок.

Занятие 2. Плоская статика (одно тело). (В аудитории решаются задачи 4.28; 4.25, на дом – 4.34).

___________________________________________________________________________

*Здесь и далее все номера задач даются по Л2.

Равновесие системы тел. (В аудитории решается задача 4.35, на дом – 4.34).

На втором занятии студент должен усвоить понятие пары сил и чем характеризуется действие пары сил на тело. Затем студенты приступают к изучению системы тел. Здесь надо очень четко усвоить, что задача системы тел состоит в определении реакций внешних и внутренних связей. Причем реакции внутренних связей могут быть определены только тогда, когда они станут внешними. Для этого необходимо провести сечение по внутренней связи, отбросить одну часть системы и рассмотреть равновесие оставшейся части.

Занятие 3. Равновесие системы тел. (В аудитории решается задача 4.41, решается задача из контрольной работы, на дом – 4.33; 4.36).

Занятие 4. Самостоятельная работа по плоской статике. (Решается студентами задача из контрольной работы на систему тел и сдаются студентами КК1 иКК2 по статике)**.

Занятия 5,6. Равновесие произвольной пространственной системы сил. (В аудитории решаются задачи 8.14, 8.28, 8.24 решается задача из контрольной работы, на дом – 8.15, 8.17, 8.36).

Занятие 7. Контрольная работа №1 по статике. Она включает в себя две задачи:

1ая – равновесие системы тел; 2ая – равновесие тела под действием произвольной пространственной системы сил.

Если студент уже написал задачу по плоской статике на занятии №4, то он решает только одну задачу по пространственной статике. На этом же занятии студент должен сделать КК3.


___________________________________________________________________________

** КК- карточный программированный контроль

Кинематика

Занятия 8,9. Кинематика точки. По заданным уравнениям движения точки х=х(t); у=у(t) необходимо определить:

траекторию точки (построить и исследовать), скорость

точки, ускорение точки и радиус кривизны траектории в указанный момент времени. (Преподаватель сам задает различные зависимости для х=х(t); у=у(t)).

На 8 занятии в аудитории решаются задачи:

х = 2sin3t + 1 х = 3t2 - 2

у = 3cos3t – 2 у = 2t

на дом:

х = 2sin2t - 3 х = 3t2

у = 2cos2t + 1 у = 2t

На 9 занятии в аудитории решаются задачи:

х = 5sin22t + 1 х = 2е-2t

у = 10cos22t – 2 у = 3е2t

на дом:

х = 2t

у = 5t2 + 2

При изучении этой темы необходимо четко усвоить, как определяются 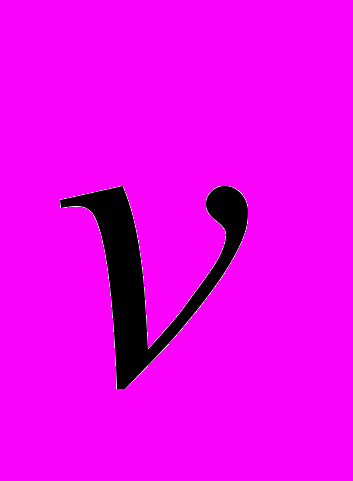, точки при координатном способе задания движения, усвоить понятия тангенциального и нормального ускорения точки, уметь определять их величину и направление.

Занятия 10, 11.Вращение твердого тела вокруг неподвижной оси. (В аудитории решаются задачи 13.2, 13.4, 13.7, 13.14, 13.18; на дом – 13.5, 13.8, 13.13, 13.19).

Занятие 12. КК4 и КК5.

Занятия 13, 14.Сложное движение точки. Определение скоростей и ускорений в случае сложного движения точки. (В аудитории решаются задачи 23.13, 23.27, 23.49, 23.47; на дом – 23.28, 23.29, 23.36).Подготовиться к контрольной работе по кинематике.

Занятие 15. Контрольная работа №2 по кинематике. Она включает в себя две задачи:

1ая – кинематика точки; 2ая – сложное движение точки.

Занятия 16,17. Плоскопараллельное движение твердого тела. Определение скоростей точек и угловых скоростей звеньев плоских механизмов. (В аудитории решаются задачи 16.14, 16.17, 16.29, 16.34; на дом – 16.15, 16.30, 16.37).


Третий семестр

Динамика

Занятия 1,2. Динамика точки. Решаются две задачи динамики точки. На первую задачу динамики в аудитории решаются задачи 26.35 и 26.9. Все остальное время решается вторая задача динамики, рассматриваются F = F(x); F = F(v); F = F(v2) и F = F(r). (В аудитории решаются задачи 27.32, 27.17 27.16; на дом – 26.15, 27.30, 27.18 и одну задачу индивидуально каждому студенту).

Надо сразу отметить, что практически на каждую тему преподаватель выдает студентам задачу из комплекта заданий, имеющихся на кафедре. Студент решает эти индивидуальные задачи в отдельной тетради, которую регулярно сдает преподавателю на проверку.

Занятие 3. Теорема о движении центра масс механической системы. (В аудитории решаются задачи 35.17, 35.19, 35.7; на дом – 35.20, 35.21 и индивидуальная задача).

Занятие 4. Теорема об изменении количества движения механической системы. (В аудитории решаются задачи 36.4, 36.9 и одна задача из комплекта индивидуальных задач; на дом – 36.8, 3 и индивидуальная задача).

Занятия 5,6. Теорема об изменении кинетического момента механической системы.

5 занятие – закон сохранения кинетического момента.

(В аудитории решаются задачи 37.53, 37.54, 37.50; на дом – 37.52, 37.56).

6 занятие – кинетический момент непостоянный. (В аудитории решаются задачи 37.43, 37.9, 37.6; на дом – 37.5, 37.57 и индивидуальная задача).

Занятия 7,8,9. Теорема об изменении кинетической энергии механической системы. (В аудитории решаются задачи 38.44, 38.42, 38.38, 47.13, 47.15; на дом – 47.9, 47.11, 38.27, 38.30).

9 занятие – решается один из вариантов курсовой работы (пункты 1,2,3).

Занятия 10,11. Принцип Даламбера. (В аудитории решаются задачи 41.17, 42.5, 42.4 и одна задача из комплекта индивидуальных задач; на дом – 41.16, 42.7, 42.8 и индивидуальная задача).

Занятие 12. Разбирается вариант из курсовой работы, решается задача с использованием принципа Даламбера.

Занятия 13,14. Принцип возможных перемещений. (В аудитории решаются задачи 46.8, 46.14, 46.17, 46.20; на дом – 46.10, 46.16 и индивидуальная задача).

Занятие 15. Общее уравнение динамики. (В аудитории решается задача 47.14 решается один из вариантов курсовой работы с помощью общего уравнения динамики; на дом – 47.3, 47.6).

Занятие 16. Уравнения Лагранжа II–го рода. (В аудитории решаются задачи 48.6, 48.35, решается один из вариантов курсовой работы, используя уравнение Лагранжа II–го рода; на дом – 48.7).

Занятие 17. Итоговое.


Межсессионный контроль

При изучении курса теоретической механики студенту предстоит написать две контрольные работы, выполнить шесть карточных контролей и курсовую работу по динамике.

Контрольная работа №1 – по статике. Проводится на 7 занятии, состоит из двух задач:

1ая – равновесие системы тел;

2ая – равновесие тела под действием произвольной пространственной системы сил.

Контрольная работа №2 – по кинематике. Проводится на 15 занятии, состоит из двух задач:

1ая – кинематика точки;

2ая – сложное движение точки.

Эти контрольные работы охватывают основные разделы курса статики и кинематики.

В процессе изучения статики и кинематики студент выполняет шесть карточных контролей по следующим темам:

КК1 – виды связей и их реакции;

КК2 – плоская статика;

КК3 – пространственная статика;

КК4 – кинематика точки;

КК5 – вращательное движение твердого тела;

КК6 – плоскопараллельное движение тела.

Эти контроли проводятся непосредственно на практических занятиях. Их выполнение является обязательным.

В третьем семестре при изучении раздела «Динамика» студент выполняет курсовую работу.

И во втором и третьем семестрах студентам выдаются индивидуально и задаются по задачнику задачи для самостоятельного решения, выполнение их является обязательным, так как это является необходимым условием усвоения материала курса.


Курсовая работа

Содержание

В курсовой работе по динамике рассматривается движение механической системы, состоящей из нескольких тел, часть из которых движется поступательно, другие вращательно, третьи совершают плоскопараллельное движение.

В работе требуется:

1. Определить скорость и ускорение точки А, пользуясь теоремой об изменении кинетической энергии.

2. Определить ускорение точки А с помощью принципа Даламбера. Определить также натяжения нитей на указанных участках.

3. Определить ускорение точки А, используя общее уравнение динамики.

4. Определить ускорение точки А с помощью уравнения Лагранжа II–го рода

Сравнить полученные результаты.

Таким образом, содержание курсовой работы охватывает почти все разделы динамики.

Требования к оформлению.

Курсовая работа выполняется на листах формата А4.

Титульный лист обязателен.

Чертежи выполняются аккуратно карандашом или на компьютере.

Текст пишется с одной стороны листа.

Название каждого раздела задания выделяется.

Курсовая работа выполняется поэтапно по мете прохождения курса и показывается преподавателю. Это дает возможность выполнить работу в срок. Среднее время на выполнение курсовой работы – 12 часов. выполненная и оформленная работа защищается у преподавателя. Для этого на кафедре разработаны специальные задания для защиты курсовой работы. Если студент самостоятельно и сознательно выполнял курсовую работу, то защита ее не вызовет затруднений. Преподаватель выставляет оценку за выполненную и защищенную работу.

Зачет

В конце второго семестра студенты сдают зачет по материалу семестра. К зачету допускаются студенты, написавшие две контрольные работы и выполнившие все шесть карточных контролей.

На зачете студент получает специальное задание, состоящее из шести небольших задач, охватывающих все разделы статики и кинематики:

1ая – по плоской статике; 2ая – по пространственной статике; 3ая – по кинематике точки; 4ая – на вращательное движение тела; 5ая – по сложному движению точки; 6ая – по плоскопараллельному движению тела.

Если студент регулярно занимался в течение семестра, ответы на задания зачета особых трудностей не вызывают.

Типовые вопросы к зачету по дисциплине

«Теоретическая механика»

Статика
  1. Виды связей и их реакции.
  2. Что такое пара сил? Чем характеризуется действие пары сил на тело.
  3. Условия и уравнения равновесия произвольной плоской системы сил (три формы). Уметь составить уравнения.
  4. Равновесие системы тел. Уметь определить реакции внешних и внутренних связей.
  5. Момент силы относительно оси.
  6. Условия и уравнения равновесия произвольной пространственной системы сил. Уметь составить эти уравнения.

Кинематика
  1. Способы задания движения точки.
  2. Определение траектории, скорости и ускорения точки при координатном способе задания ее движения.
  3. Определение скорости и ускорения при естественном способе задания движения точки. Касательное и нормальное ускорения.
  4. Вращение твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение тела. Определение скорости и ускорения точки тела, вращающегося вокруг неподвижной оси.
  5. Плоскопараллельное движение твердого тела. Уравнения движения, разложение движения на составляющие.
  6. Определение скоростей точек плоской фигуры. Мгновенный центр скоростей, его свойства и способы определения.
  7. Сложное движение точки. Переносное, относительное и абсолютные движения. Уметь определять величину и направление кориолисова ускорения.

Экзамен

В конце третьего семестра студенты сдают экзамен по всему курсу.

Экзаменационное задание включает в себя три задачи:

1ая – по статике;

2ая – по кинематике;

3ая – по динамике.

Первые две задачи достаточно простые, студент просто должен продемонстрировать навык и знания при решении задач статики и кинематики. Третья задача – по динамике, по всем разделам курса «Динамика».

4ыйвопрос – теоретический вопрос по динамике.

Студент обязан ответить на все вопросы билета.


Типовые вопросы к экзамену по дисциплине

«Теоретическая механика»
  1. Предмет динамики. Законы динамики.
  2. Дифференциальные уравнения движения точки в векторной форме и проекциях на оси координат. Две основные задачи динамики точки.
  3. Динамика относительного движения точки. относительный покой. Принцип относительности классической механики.
  4. Теорема о движении центра масс системы. Следствия.
  5. Теорема об изменении количества движения точки и механической системы. Следствия.
  6. Понятие о моментах инерции твердого тела относительно плоскости, оси и полюса. Теорема о моментах инерции тела относительно параллельных осей моменты инерции некоторых тел.
  7. Теорема об изменении момента количества движения точки. Следствия.
  8. Теорема об изменении кинетического момента системы. Следствия.
  9. Понятие о работе. Элементарная работа силы. Работа силы на конечном пути. Примеры вычисления работы некоторых сил.
  10. Теорема об изменении кинетической энергии точки.
  11. Теорема об изменении кинетической энергии механической системы.
  12. Понятие о силовом поле. Силовая функция. Работа сил потенциального силового поля.
  13. Потенциальная энергия. Связь силовой функции и потенциальной энергии. Закон сохранения полной механической энергии.
  14. Динамика твердого тела. Дифференциальные уравнения поступательного, вращательного и плоскопараллельного движения тела.
  15. Принцип Даламбера для материальной точки. Метод кинетостатики. Принцип Даламбера для механической системы.
  16. Приведение сил инерции точек твердого тела к центру. Главный вектор и главный момент сил инерции.
  17. Виды связей и их уравнения. Классификация связей.
  18. Принцип возможных перемещений.
  19. Общее уравнение динамики.
  20. Обобщенные координаты. Выражение возможной работы в обобщенных координатах. Обобщенные силы.
  21. Условия равновесия механической системы в обобщенных координатах.
  22. Связь обобщенной силы и потенциальной энергии. Условия равновесия механической системы для консервативных систем в обобщенных координатах.
  23. Понятие об устойчивости равновесия.
  24. Уравнения Лагранжа II – го рода.



Список литературы,

рекомендуемой кафедрой «Теоретическая механика»


Л1. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. – М.,: Высшая школа. 1983г. 575 с.

Л2. Мещерский И.В. Сборник задач по теоретической механике. Наука. 1981г. 480 с.


Методические указания (МУ)

На кафедре изданы методические указания по решению задач практически по всем разделам курса теоретической механики.

Статика.
  1. Александрова С.Г., Мозгунов В.Н., Серов М.В. Введение в статику. – М.,: МИХМ. 1987г. 18 с.
  2. Смоленцев Ю.А., Деханов В.И. Решение задач о равновесии твердого тела и системы тел под действием произвольной плоской системы сил. – М.,: МИХМ. 1987г. 27 с.
  3. Александрова С.Г., Мозгунов В.Н. Решение задач по пространственной статике. – М., МИХМ. 1987 г. 26 с.

Кинематика.
  1. Александрова С.Г., Серов М.В., Деханов В.И. Решение задач по кинематике сложного движения точки. – М.,: МГАХМ. 1994г. 24 с.
  2. Александрова С.Г., Серов М.В. Решение задач по кинематике плоскопараллельного движения твердого тела. – М.,: МГУИЭ. 2001г. 30 с.

Динамика
  1. Серов М.В., Александрова С.Г. Решение задач динамики с помощью теоремы о движении центра масс. – М.,: МГУИЭ. 2001г. 20 с.
  2. Серов М.В., Александрова С.Г. Решение задач динамики с помощью теоремы об изменении количества движения. – М.,: МГУИЭ. 2001г. 20 с.
  3. Александрова С.Г., Серов М.В., Деханов В.И. Решение задач динамики с помощью теоремы о движении центра масс. – М.,: МГУИЭ. 2001г. 20 с.
  4. Александрова С.Г., Деханов В.И. Решение задач динамики с применением теоремы об изменении кинетической энергии. – М.,: МИХМ. 1990г. 28 с.
  5. Смоленцев Ю.А. Решение задач с применением принципов механики. – М.,: МИХМ. 1990г. 28 с.