Лекция 11. Основные вопросы, выносимые на обсуждение на предыдущей лекции
| Вид материала | Лекция |
- Лекция Темы обсуждений предыдущей лекции, 112.29kb.
- Лекция поведение потребителя, 61.41kb.
- Лекция 4 основы теории спроса и предложения, 43.74kb.
- Лекция Расчет основных термодинамических величин ΔU,, 283.92kb.
- В. В. Управление персоналом. М.: Академия, 2003. 528 с. Лекция, 1904.58kb.
- Основы спектрального анализа звуков, 76.67kb.
- Лекция: Планирование процессов, 482.91kb.
- Темы и вопросы, выносимые в устную часть экзамена по этнологии. Новейший свет, 20.47kb.
- Изучение теоретической механики, 209.36kb.
- Лекция 10: Теория чисел-2, 147.71kb.
ЛЕКЦИЯ 11.
Основные вопросы, выносимые на обсуждение на предыдущей лекции:
1. Рассмотрели примеры двухфакторных моделей. В качестве еще одного примера можно рассмотреть следующую модель:
Эта модель основана на модели остаточной чистой прибыли (Residual earnings model – REM), которая предполагает, что фундаментальная ценность собственного капитала организации складывается из двух элементов. Во-первых, из Et-1 - балансовой стоимости собственного капитала на момент оценки;
Во-вторых, REt*-величины прироста фундаментальной стоимости над балансовой, определяемой, в свою очередь, как бесконечный поток остаточных чистых прибылей, дисконтированных по ставке затрат на собственный капитал. Последний, в свою очередь, при определенных допущениях есть перпетуитет фактически наблюдаемого значения остаточной чистой прибыли за прошлый период (t - 1, t).
2. Вели понятия многофакторной регрессионной модели и функции регрессии. Получили систему нормальных уравнений для оценивания параметров многофакторной функции регрессии в скалярной и матричной форме.
^ 3. Построили доверительные интервалы для неизвестных параметров функции регрессии и неизвестной дисперсии
На этой лекции рассмотрим, каким образом осуществляется прогнозирование при помощи многофакторной регрессии, и приведем формулу для интервальной оценки прогноза.
^ Обозначим через
следующий вектор: =
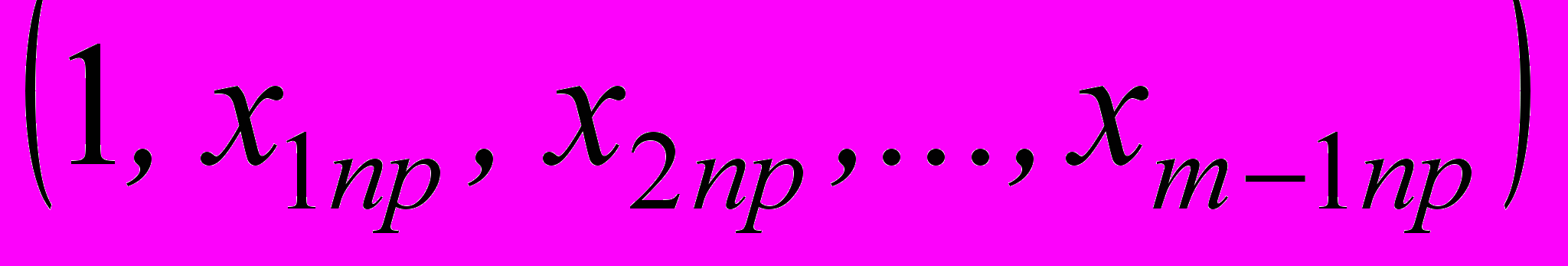. Запись
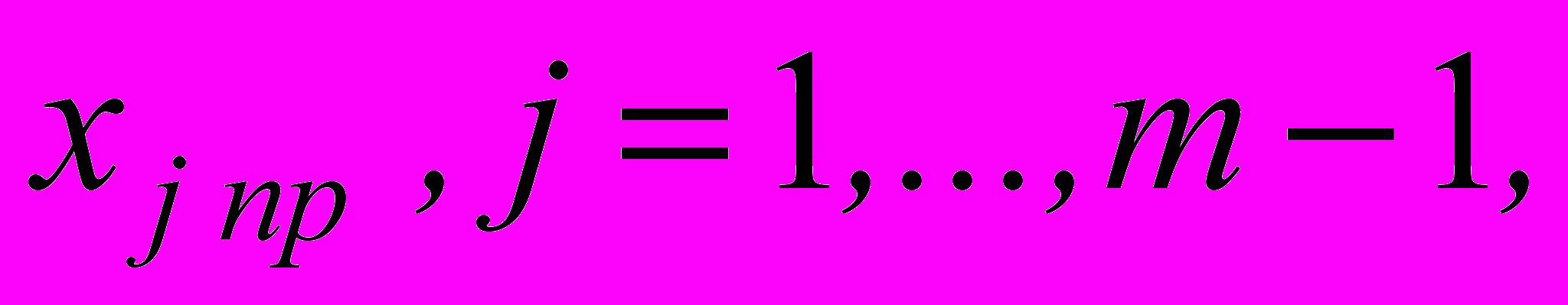
означает прогнозируемое значение фактора с номером j. Тогда в матричной форме прогнозируемое значение результирующего признака можно записать так:
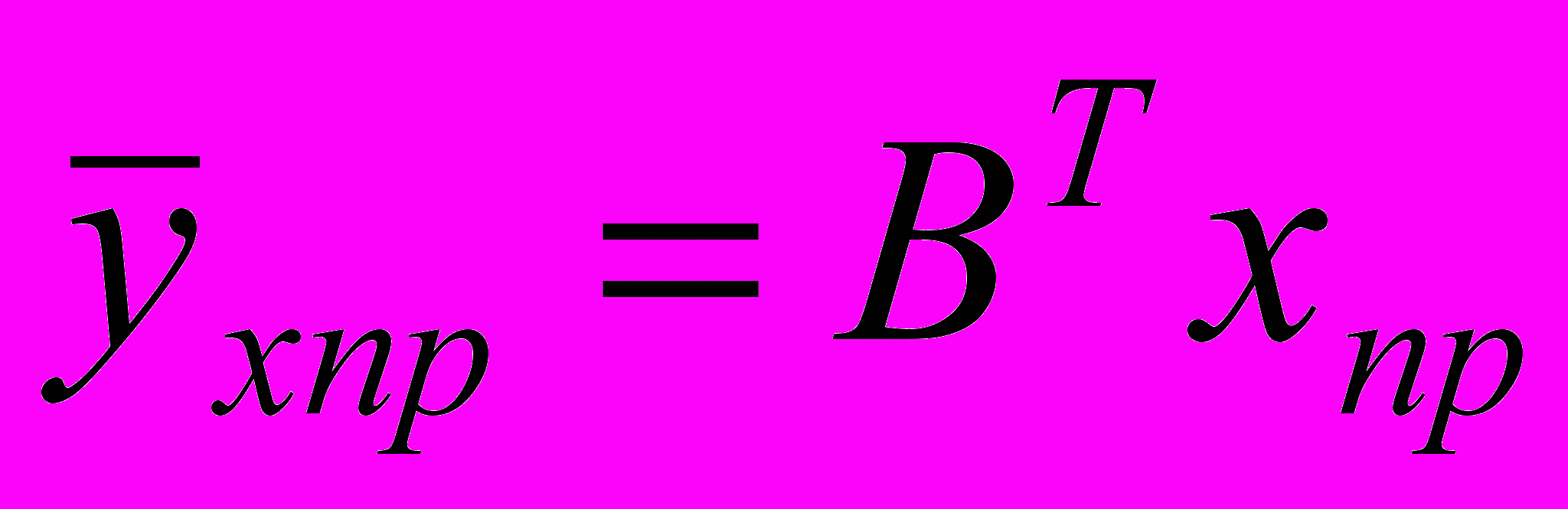, (3.2.6)а в скалярной форме так:
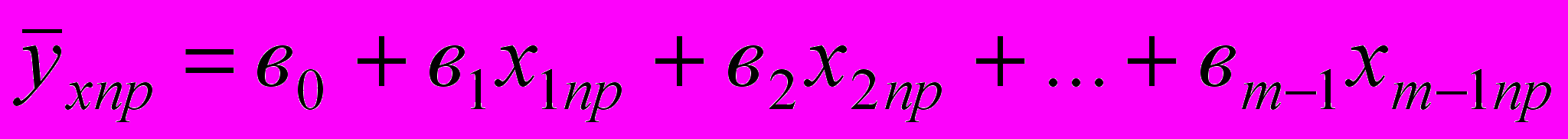. (3.2.7)Доверительный интервал для неизвестного условного математического ожидания
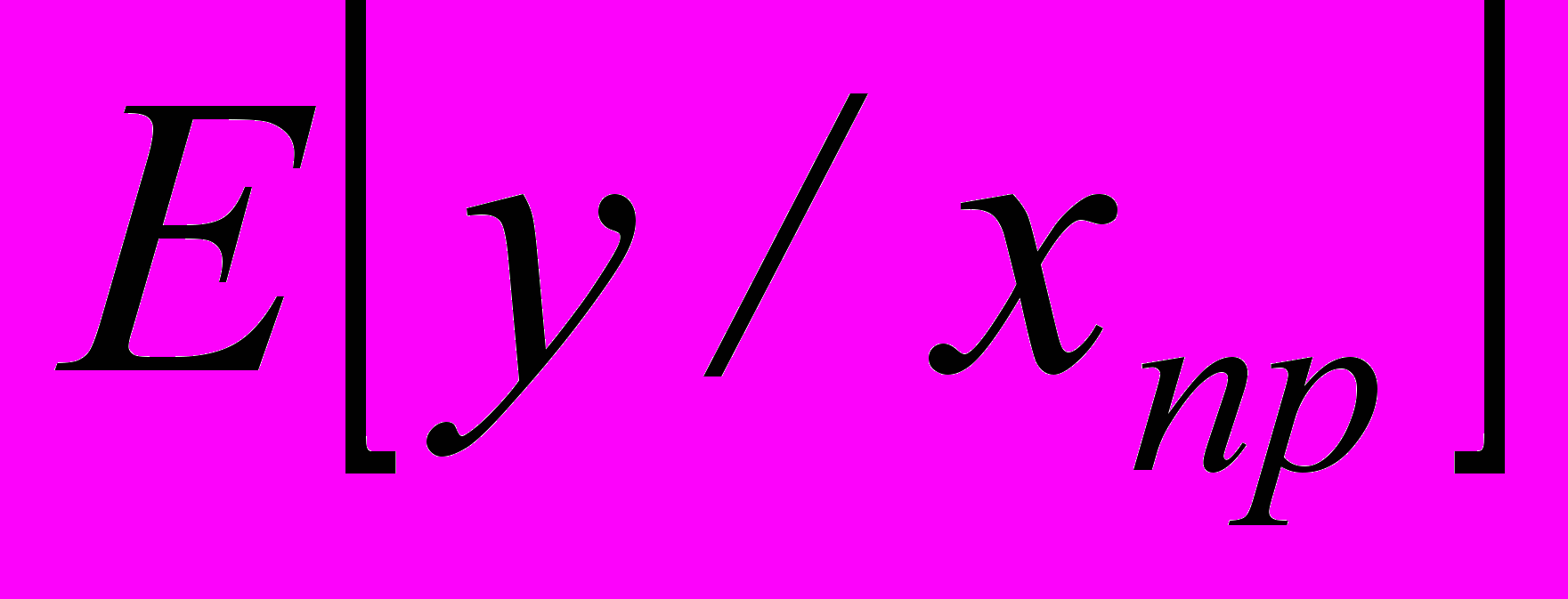будет иметь вид:
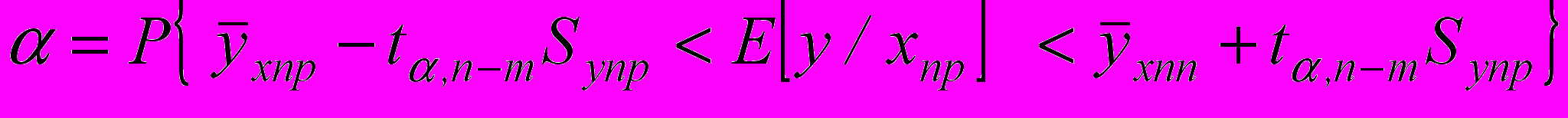(3.2.8)где
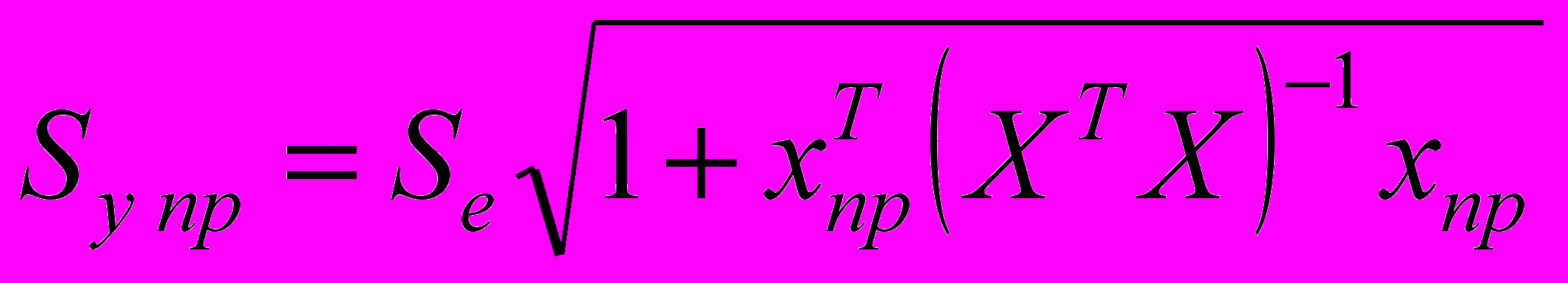. (3.2.9)^
3.3. Множественный коэффициент детерминации
Введем понятие множественного коэффициента детерминации. Как и в параграфе 2.4 будем использовать следующие обозначения:
TSS =
, ESS=
где
=
Определение 3.3.1.Множественным коэффициентом детерминации (выборочным) называют следующую величину:
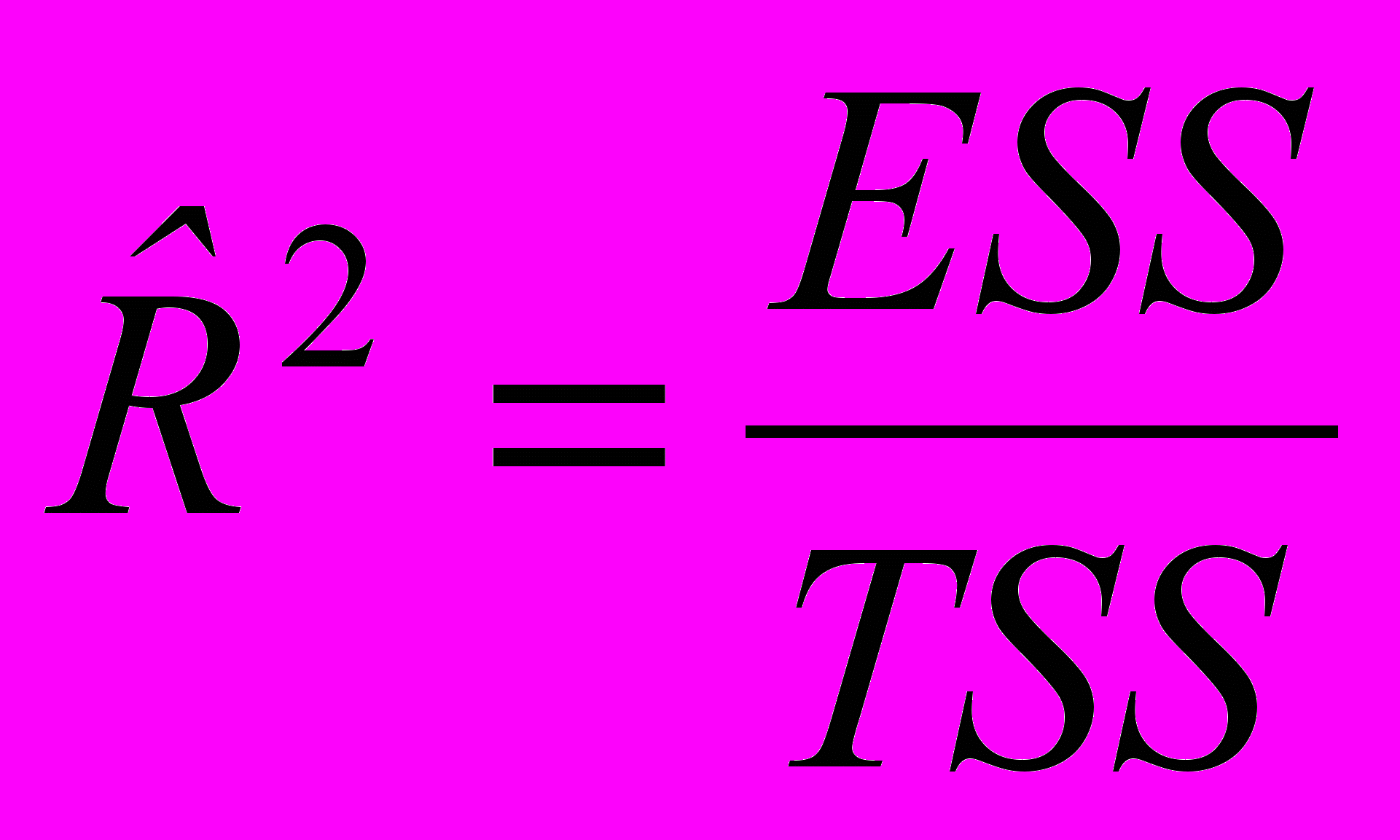. (3.3.1)Замечание 1. Формулы для вычисления TSS и ESS в матричной форме записи будут иметь вид:
ТSS=
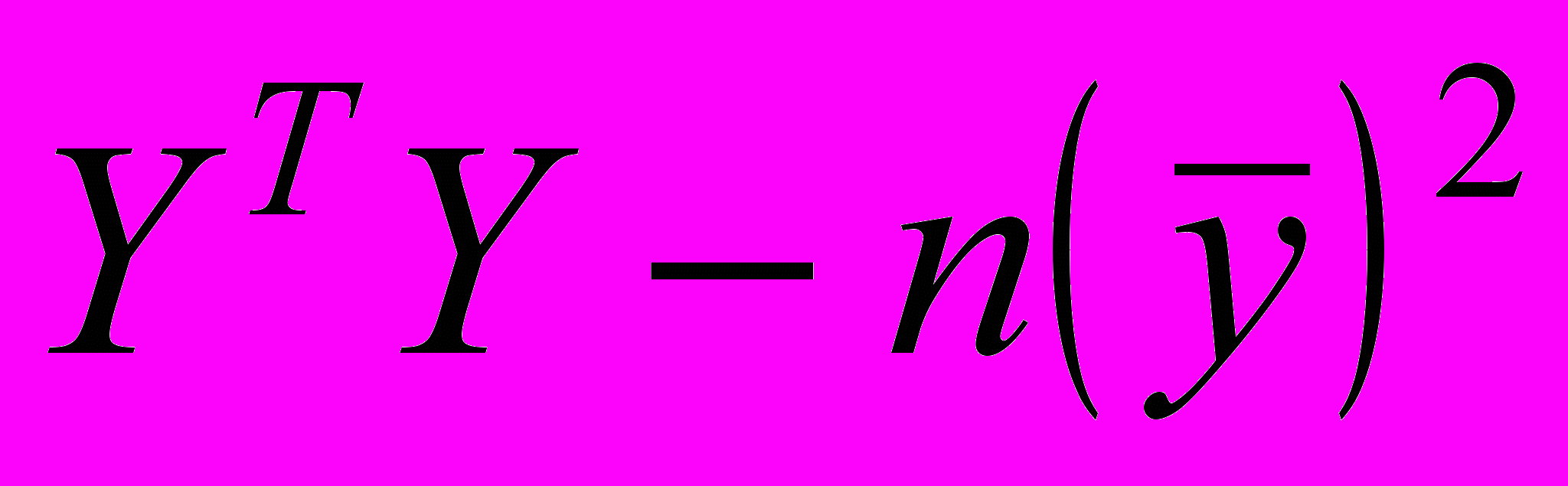, (3.3.2)ESS=
. (3.3.3)Следовательно,
. (3.3.4)Отметим, что множественный коэффициент детерминации
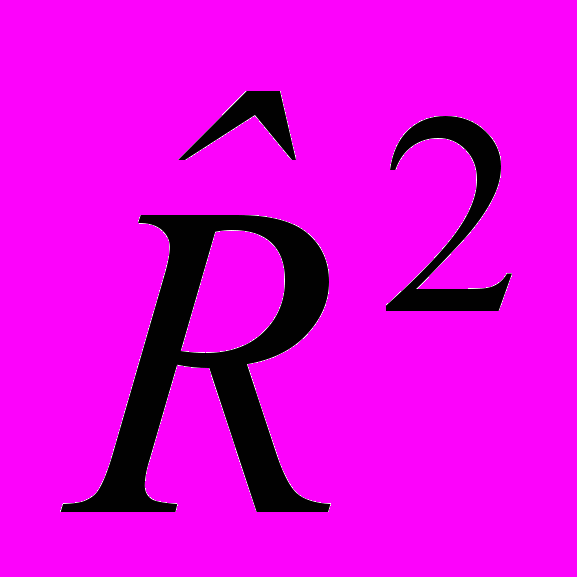характеризует, какая доля вариации (изменения) результирующего признака y определяется совместным изменением независимых факторов 
. Значения
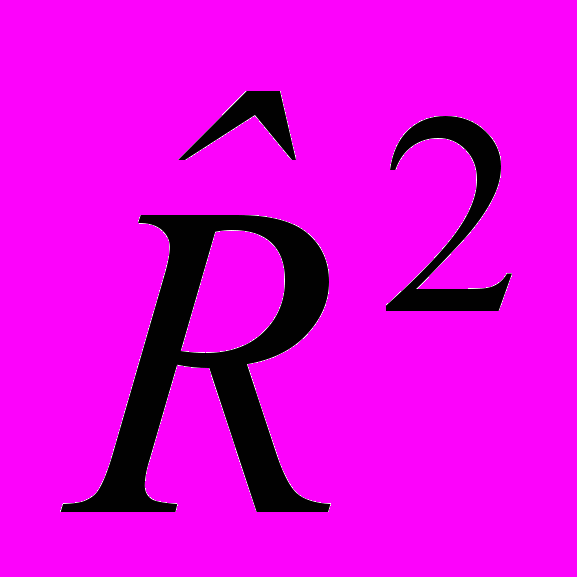принадлежат отрезку [0;1]. Чем ближе величина 
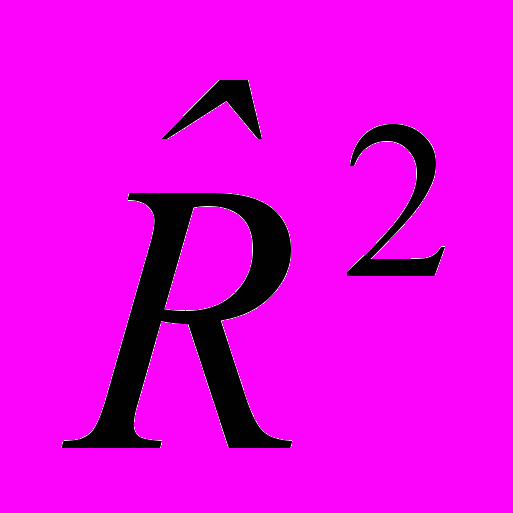к 1, тем больше у нас оснований быть уверенными в правильности выбора линейной многофакторной модели (3.1.4) для аппроксимации значений у.Множественный коэффициент детерминации обладает следующим свойством:
введение нового m-го фактора в регрессионную модель, по крайней мере, не уменьшает значение
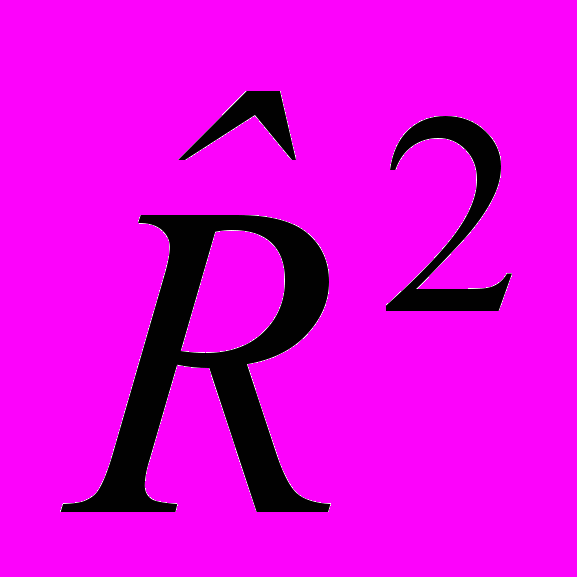.К чему это может привести на практике? Мы можем ввести в регрессионную модель достаточно большое число факторов и за счет увеличения их количества, а не за счет их реального влияния на переменную y, увеличить значение
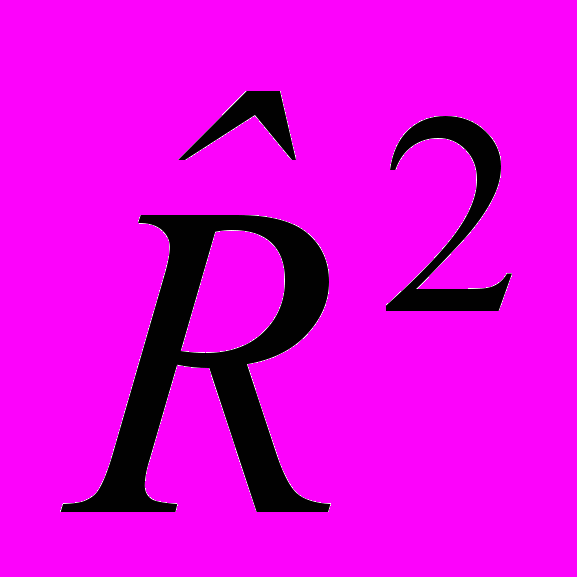. Это, в свою очередь, может привести к ошибочному выводу о значимости влияния факторов на y. Для того чтобы компенсировать влияние такого эффекта при включении в модель нового фактора, вводят понятие скорректированного коэффициента детерминации.Определение3.3.2. Скорректированным коэффициентом детерминации называют следующий показатель:
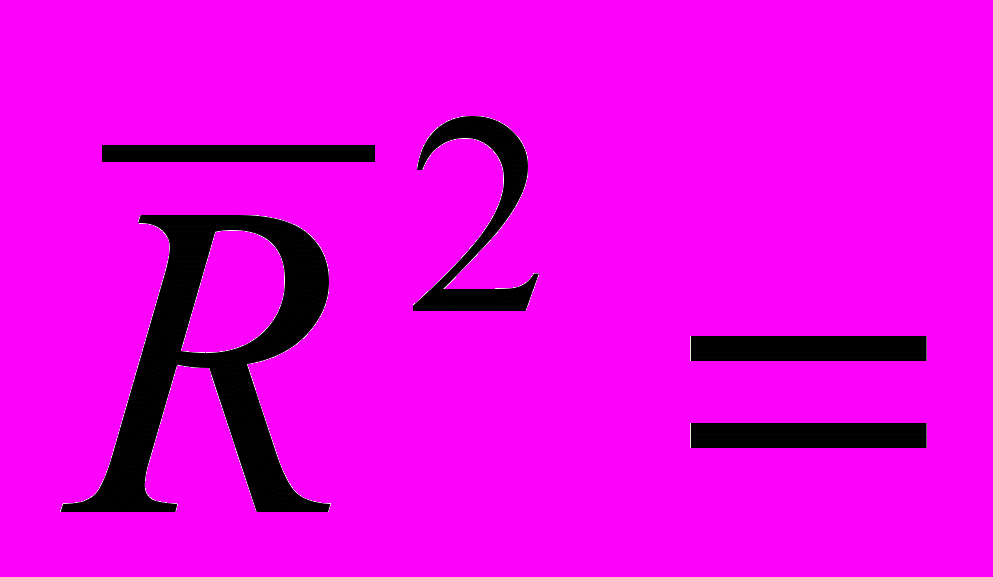
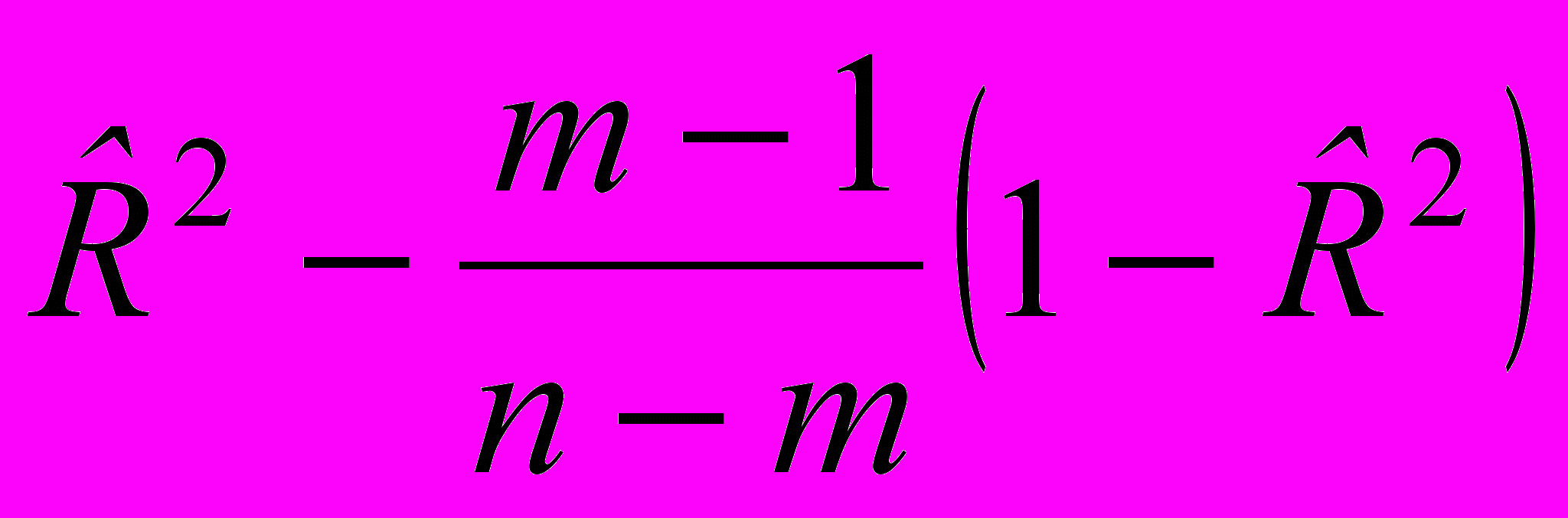. (3.3.5)Замечание 2. Формула (3.3.5) эквивалентна формуле 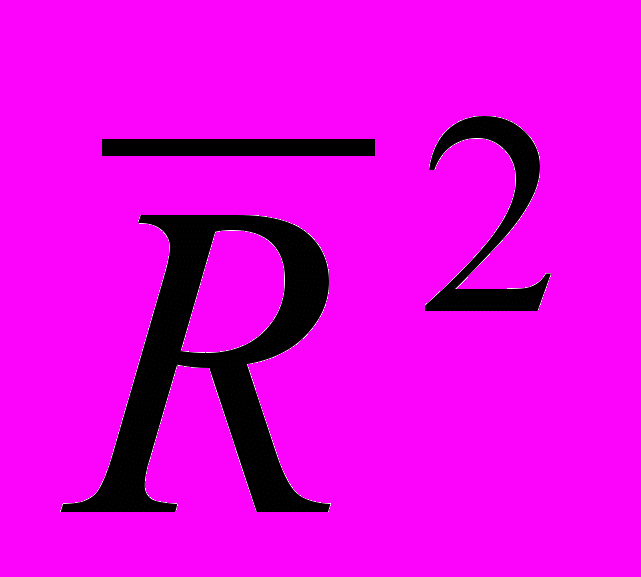(3.3.6):
= 
. (3.3.6)Замечание3. Скорректированный коэффициент детерминации
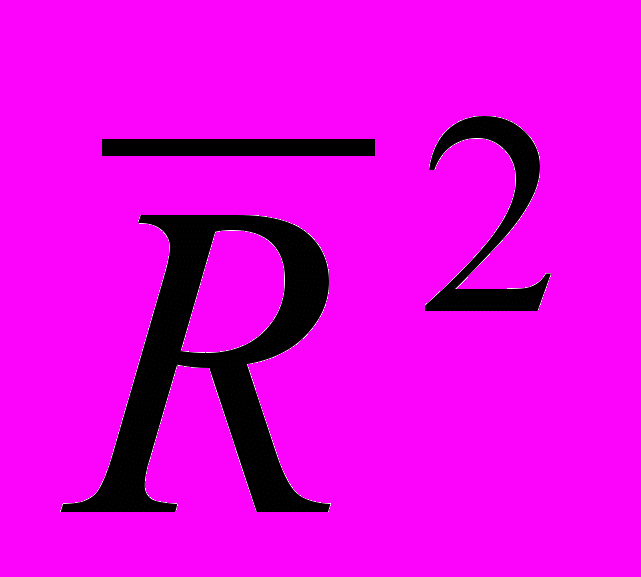может принимать и отрицательные значения. Значения скорректированного (нормированного) коэффициента детерминации приводятся в итоговой таблице процедуры «РЕГРЕССИЯ».| | Регрессионная статистика | |
| | Множественный R | 0,913 |
| | R-квадрат | 0,834 |
| | ^ Нормированный R-квадрат | 0,831 |
| | Стандартная ошибка | 8,276 |
| | Наблюдения | 124,000 |
| | | |
Замечание 4. Скорректированный коэффициент детерминации
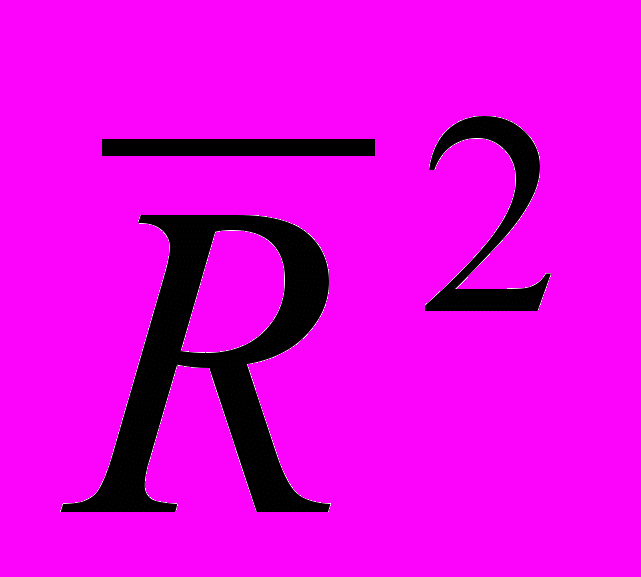не превосходит по величине множественный коэффициент детерминации: .^
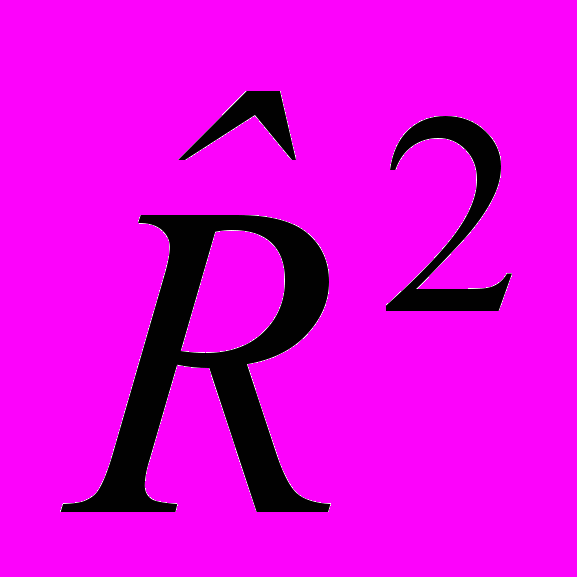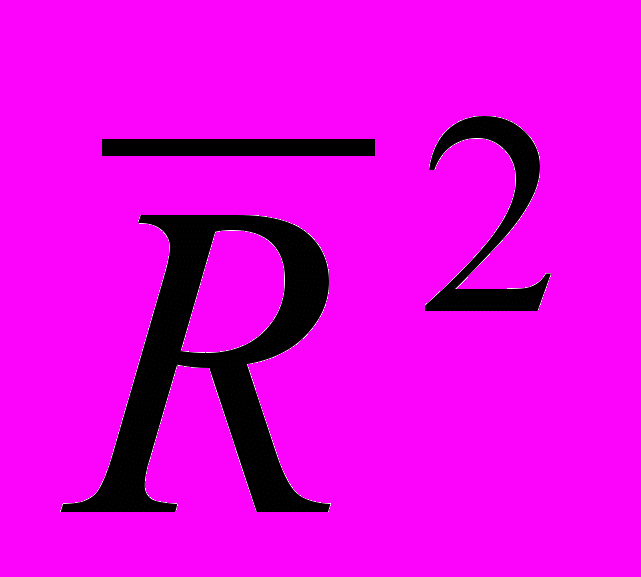
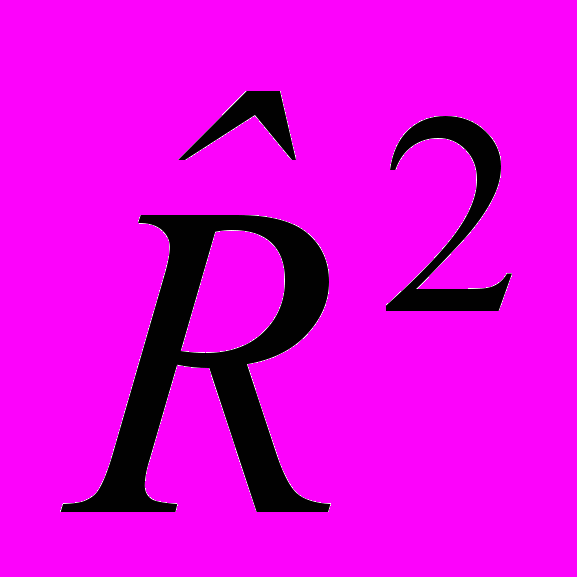3.4. Проверка гипотез о значимости многофакторной регрессионной модели.
Как отмечалось выше, величина множественного коэффициента детерминации может служить ориентиром при ответе на вопрос, насколько мы правы, выбрав в качестве модели линейную регрессионную модель. Для дальнейшего анализа необходимо провести статистическую проверку гипотез о значимости, как всей модели, так и входящих в нее факторов.
^ Основная гипотеза для проверки значимости многофакторной регрессионной модели формулируется следующим образом:
Для проверки основной гипотезы вычисляют выборочную статистику:
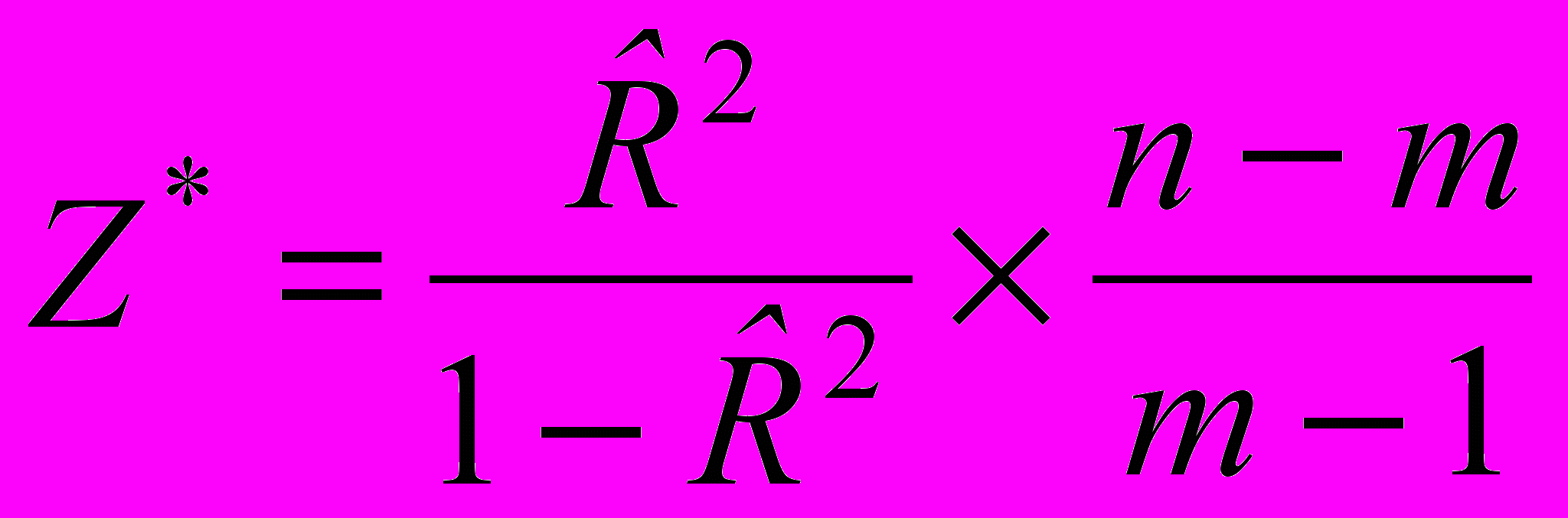. (3.4.2)Если гипотеза H0 верна, то статистика (3.4.2) имеет распределение Фишера c 1=(m-1), 2=(n-m) степенями свободы (Z*=Fm-1,n-m.). Критическая область является, правосторонней её границу K2 ищут по заданному уровню значимости 1- и 1=(m-1), 2=(n-m) степеням свободы по таблицам распределения Фишера.
Если
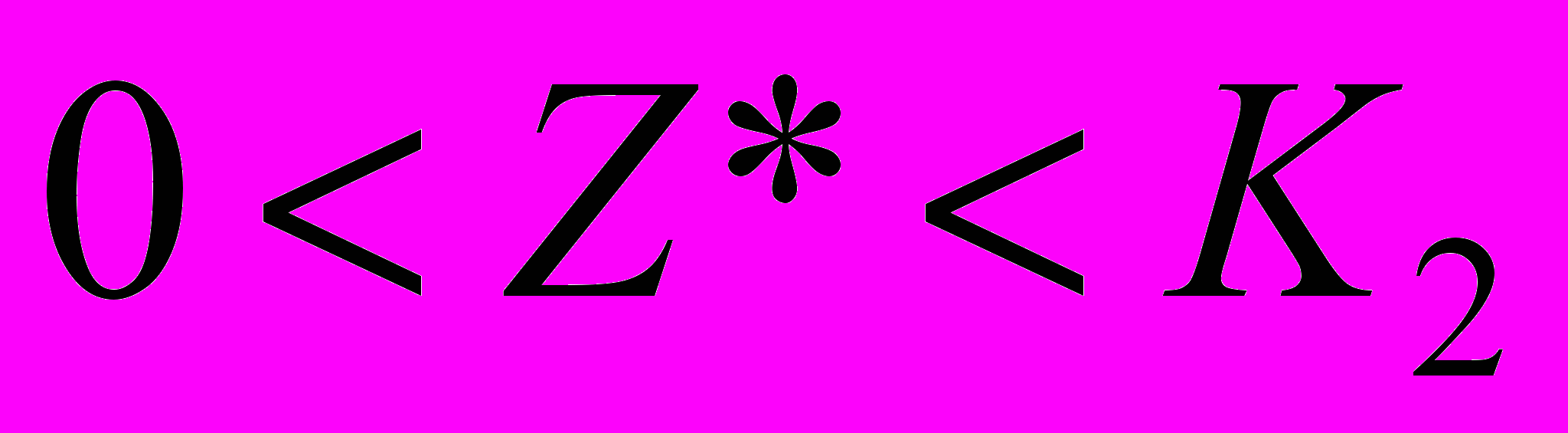,то принимают гипотезу H0, в противном случае, когда выполняется неравенство
, принимают альтернативную гипотезу. Во втором случае говорят, что уравнение регрессии статистически значимо.
Очень важным при работе с многофакторной регрессией является процесс выделения наиболее существенных факторов модели. То есть выявления степени влияния конкретного фактора на результирующий признак. Проверка значимости фактора хк сводится к статистической проверке значимого отличия от нуля стоящего перед ним коэффициента к.
Относительно каждого коэффициента, стоящего перед независимой переменной в многофакторной регрессионной модели, формулируют основную и альтернативную гипотезы вида:
(3.4.3)Затем вычисляют выборочную статистику вида:
Z*=
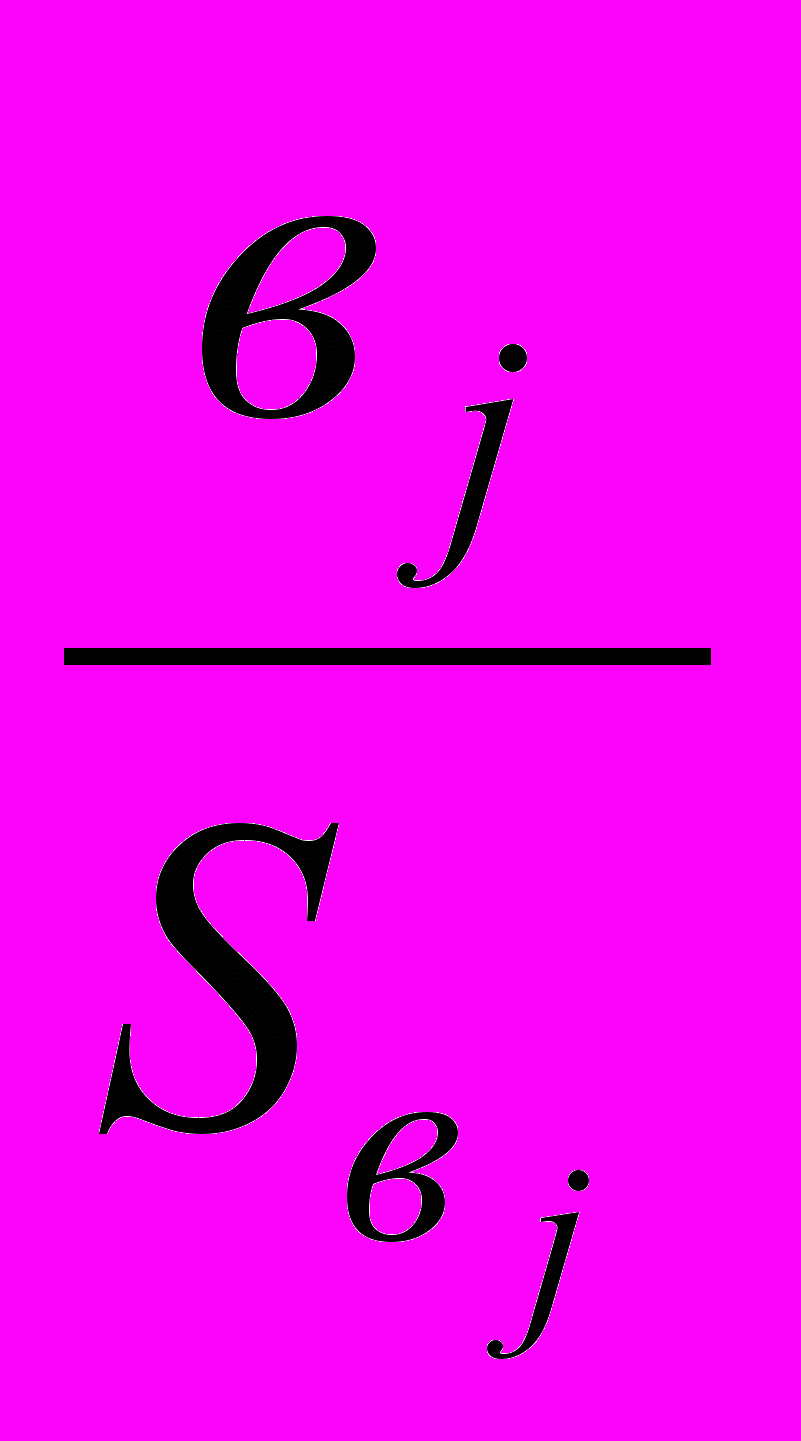. (3.4.4)В том случае, если основная гипотеза верна, статистика (3.4.4) будет иметь распределение Стьюдента c (n-m) степенями свободы
(Z*=tn-m). Критическая область будет двусторонней, К1= - К2. Граничное значение К2 ищут по таблицам распределения Стьюдента по заданному уровню значимости (1-) и (n-m) степеням свободы.
Если
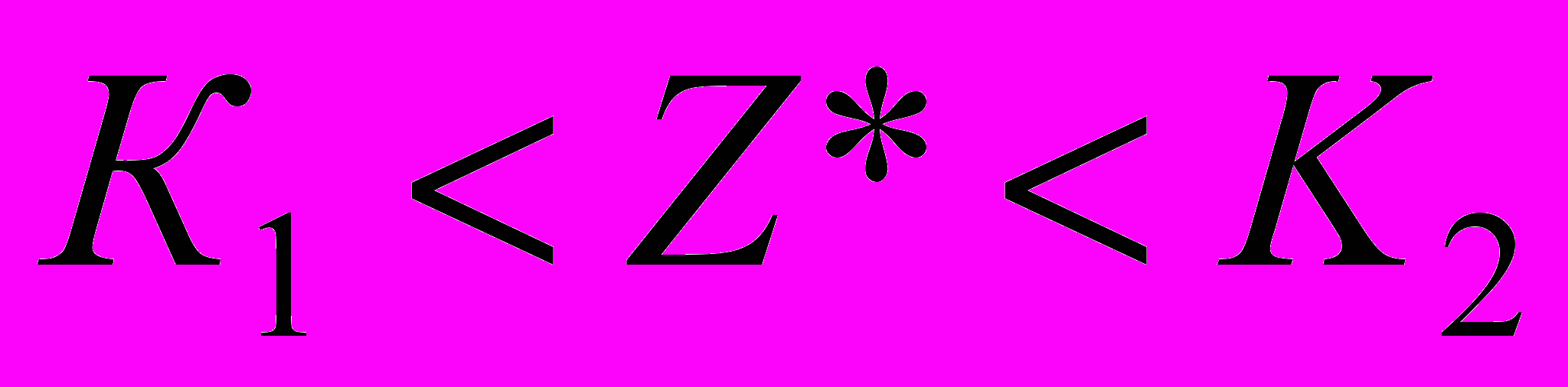, то принимают основную гипотезу и считают, что коэффициент 
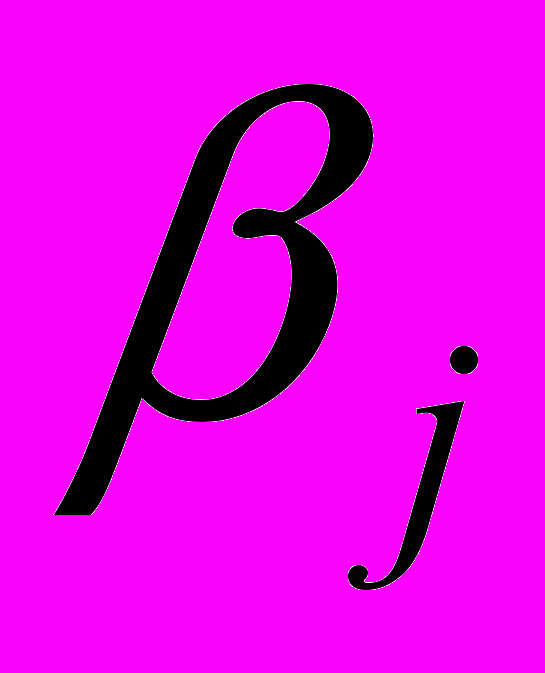незначимо отличается от нуля (или просто незначим). Альтернативную гипотезу принимают, ес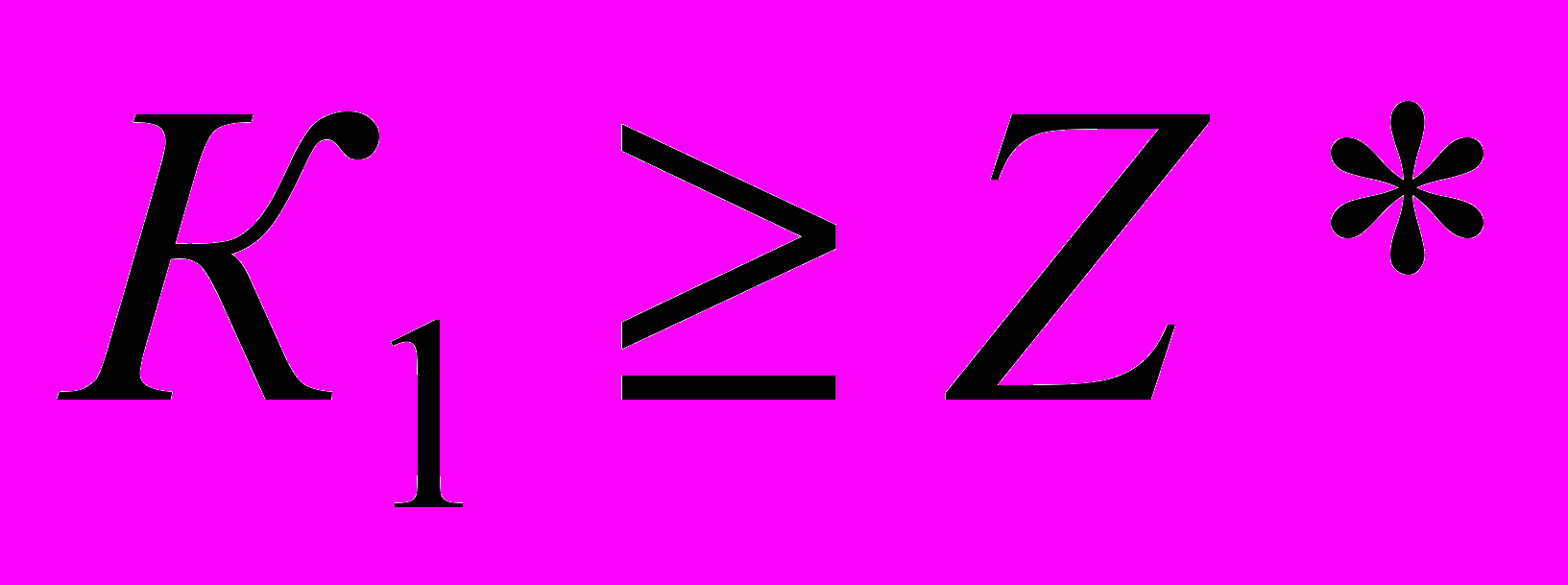ли 
или . В этом случае говорят, что коэффициент
значимо отличается от нуля. ^ Та переменная (фактор) xj, которой соответствует незначимый коэффициент
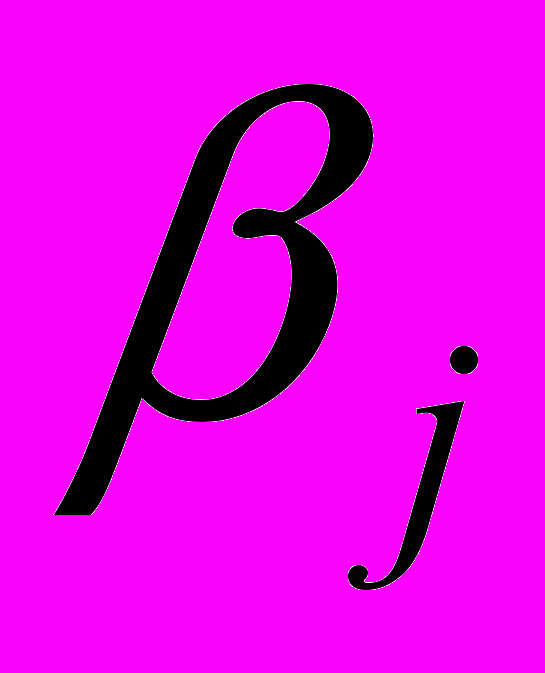, также считается незначимой и заслуживает того, чтобы усомниться в необходимости ее включения в уравнение регрессии. Может быть, в дальнейшем стоит рассмотреть регрессионную модель, в которой переменной xj, уже не будет.| t-статистика |
| 2,419 |
| 22,850 |
| 11,632 |
^
3.5. Частные коэффициенты корреляции.
В первой главе мы уже говорили о выборочной ковариационной и корреляционной матрице для двух случайных величин. Для дальнейших рассуждений рассмотрим структуру таких матриц в общем случае, уже для нескольких случайных величин.
Обозначим через
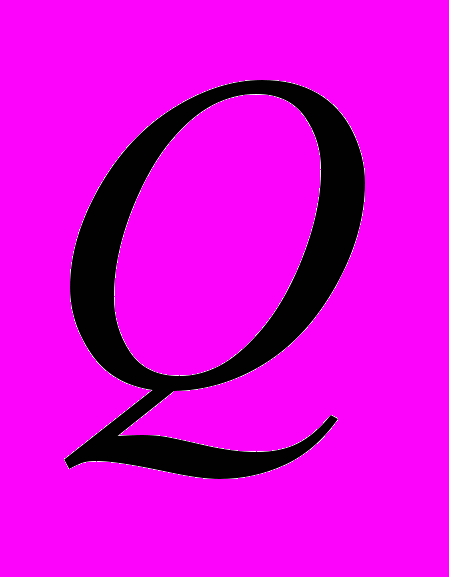и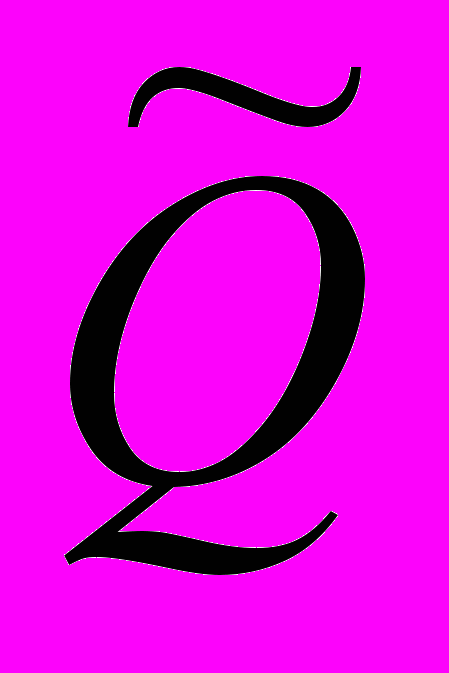 
следующие матрицы выборочных коэффициентов корреляции между результирующим признаком и факторами в модели множественной и между факторами.
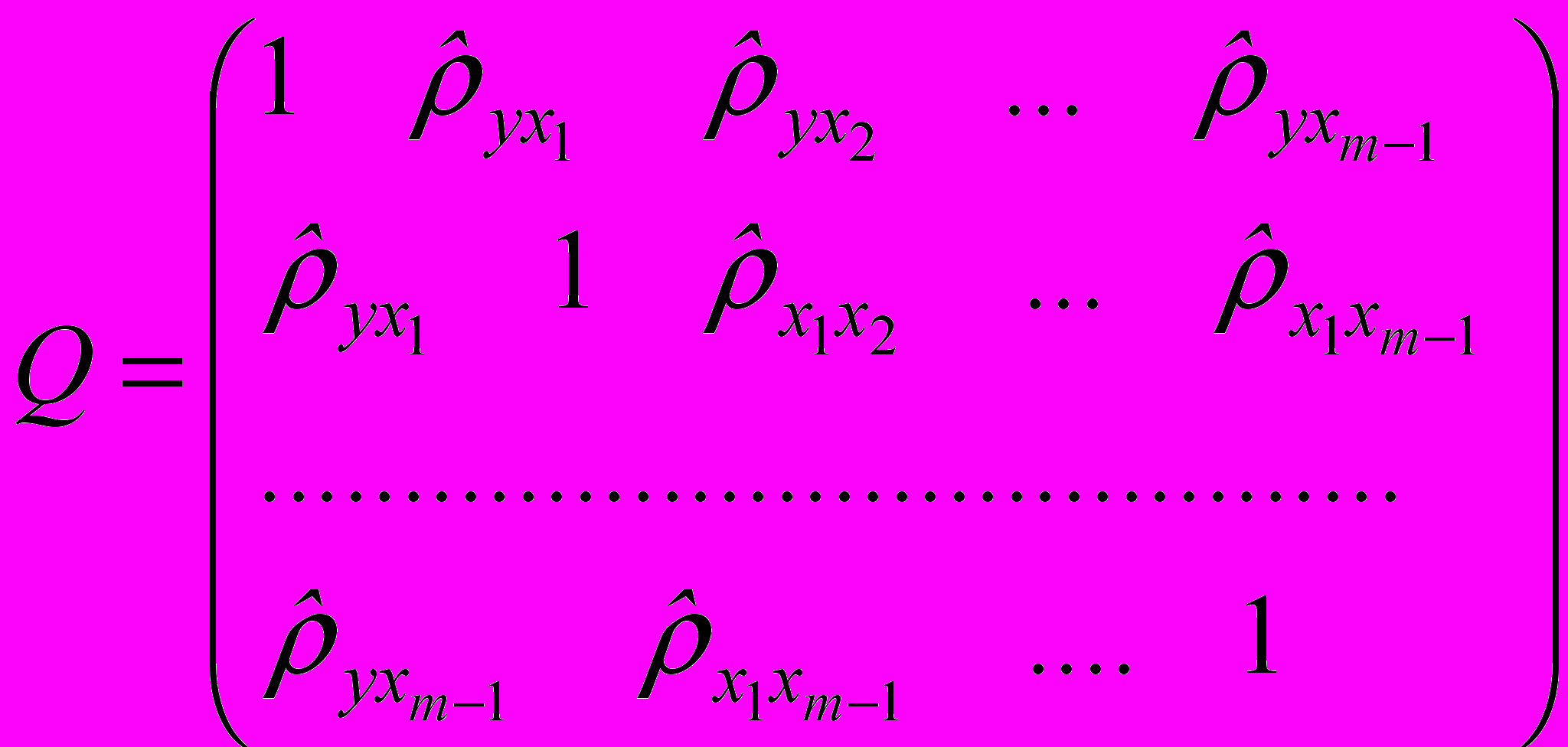, (3.5.1)
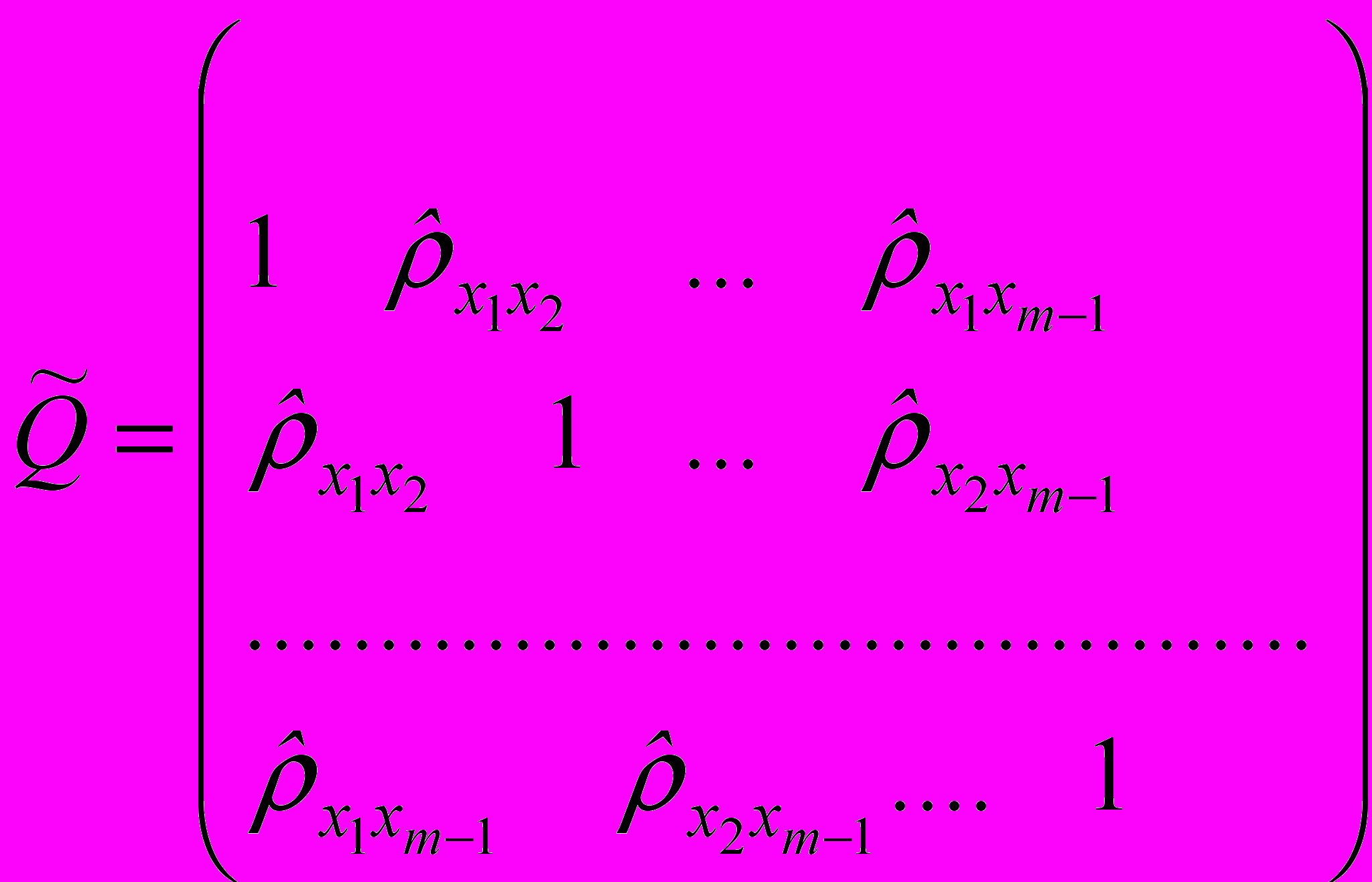. (3.5.2)Очевидно, что
.Образуя некоторую упорядоченную систему, факторы оказывают совместное воздействие друг на друга. Поэтому, введем такую числовую характеристику, которая служит мерой силы связи между двумя переменными такой системы, «очищенной» от влияния остальных. Такая статистическая характеристика называется частным коэффициентом корреляции между двумя факторами.